Class 9 Math: Sample Question Paper- 5 (With Solutions) PDF Download
SECTION - A
Questions 1 to 20 carry 1 mark each.
Q.1. Rationalisation of denominator of 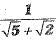 gives:
gives:
(a) 1/√10
(b) 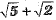
(c) 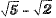
(d) 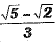
Ans. 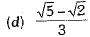
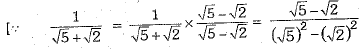
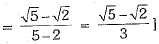
Q.2. The number of terms in the expansion of (a + b + c)n, where n ∈ N is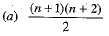
(b) n + 2
(c) n + 1
(d) n(n + 1)
Ans. Choice (a) is correct.
We have (a + b + c)n = {a + (b + c )}n = an + nC1 an - 1(b + c) + nC2 an-2(b + c)2 + ....+ nCn(b + c)n
On expanding each term of R.H.S we get
Number of term in first term = 1
Number of terms in second term = 2
Number of terms in third term = 3
Number of terms in fourth term = 4
..........................................................
..........................................................
Number of terms in (r + 1)th term = n + 1
∴ Total number of terms = 1+ 2 + 3 + ... + (n + 1)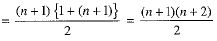
Q.3. The area of the trapezium formed by the lines x = 0, x = 2, y = 4 and x + y = 2 is (in sq units)
(a) 6
(b)8
(c) 10
(d) 12
Ans. (a)
∴ Area of trapezium ABCD = 1/2 x (BC + AD) x CD
= 1/2 x (2 + 4) x 2
= 6 sq units
Q.4. Ordinate of all points on the x-axis is
(a) 0
(b) 1
(c) -1
(d) any number
Ans. (a)
Because ordinate or y-y-coordinate of a point is perpendicular distance to the x-axis measured along the y-axis. If a point lies on x-axis, then the perpendicular distance of a point from x-axis will be zero, so ordinate will be zero.
Q.5. Two angles measure (30 - α)° and (125 + 2α)°. If each one is the supplement of the other, then the value of a is:
(a) 45°
(b) 35°
(c) 25°
(d) 65°
Ans. (c) 25°
[∵ Angles (30 - α)° and (125 + 2α)° are supplement of each other.
∴ (30 - α)0 + (125 + 2α)° = 180°
⇒ 30 - α + 125 + 2α = 180°
⇒ α + 155° = 180°
⇒ α = 180° - 155° ⇒ α = 25°]
Q.6. When three coins are tossed simultaneously then the number of elements in the sample space of the random experiment is
(a) 8
(b) 9
(c) 4
(d) 16
Ans. Choice (a) is correct.
Because when three coins are tossed simultaneously, the sample is
{HHH, HHT, HTH, THH, HTT, THT, TTH, TTT} and it has 8 elements.
Q.7. One of the solution of 2x + 3y = 3, is
(a) (1, 0)
(b)(1, 1)
(c) (0, 1)
(d) (o, 0)
Ans. (c) When x = 0, then
2 (0) + 3y = 3 ⇒ 3y = 3 ⇒ y = 1
Q.8. The radius of a sphere is 2r, then its volume will be
(a) 4/3 πr3
(b) 4πr3
(c) 8πr3/3
(d) 32/3 πr3
Ans. (d)
Volume of the sphere = 4/3πR3
But radius R = 2r
Therefore, volume of the sphere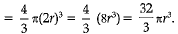
Q.9. Volume of cone of radius r/2 and height '2h' is:
(a) 1/3 πr2h
(b) 1/4 πr2h
(c) 1/5 πr2h
(d) 1/6 πr2h
Ans. (d) 1/6 πr2h
[∵ Volume of cone = 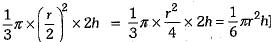
Q.10. The coordinates of the point which bisects the line segment joining the points A(2, 3, 7) and B(6, 1, 5) are
(a) (6,2,4)
(b) (2,4,6)
(c) (6,4,2)
(d) (4,2,6)
Ans. Choice (d) is correct.
The coordinates of the point that bisects the line segment joining the points A(2, 3, 7) and B(6, 1, 5) are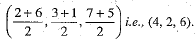
(Q. Nos. 11-15) Fill in the blanks
Q.11. A polynomial of one term is called a .......
Ans. A polynomial of one term is called a monomial.
Q.12. If two interior angles on the same side of the transversal intersecting two parallel lines are in the ratio 2 : 3, then the greater of the angles is 108°.
Ans. True
Let the angles be 2x and 3x
2x + 3x = 180° (co-interior angles)
⇒ 5x = 180°
⇒ x = 36°
2x = 72°, 3x = 108°
The greater angle is 108°
Q.13. In any quadrilateral, if a pair of opposite sides is equal as well as parallel, it is a ......
OR
"In a quadrilateral, if diagonals bisect each other, then it is α .....".
Ans. Parallelogram
Or
Parallelogram.
Q.14. The centre of the circle x2 + y2 + 6x + 2y = 0 is.
OR
If the line ax + by + c = 0 is a diameter of the circle x2 + y2 = 4, then the value of c is _________ .
Ans. (- 3, - 1)
The given circle is x2 + y2 + 6x + 2y = 0
⇒ x2 + 6x + 9 + y2 + 2y + 1 = 9 + 1
⇒ (x + 3)2 + (y + 1)2 =10
⇒ {x - ( - 3)}2 + {y - (-1))2 = 10
Thus, the centre of the circle is (- 3, - 1).
OR
Solution. 0
Given circle is a2 + y2 = 4
⇒ (x - 0)2 + (y - 0)2 = 22
⇒ (0, 0) is centre and 2 units is the radius of the given circle.
Now, since ax + by + c - 0 is a diameter therefore (0, 0) must lie on it.
⇒ a.0 + b.C + c = 0
⇒ 0 + 0 + c = 0
⇒ c = 0
Q.15. The area of a rhombus is half the .......... sides and .......... between them.
Ans. (Parallel sides, perpendicular distance)
Area of rhombus = 1/2(sum of parallel sides) x (perpendicular distance between them)
(Q. Nos. 16-20) Answer the following questions.
Q.16. Represent -7/5 on the number line.
Ans. 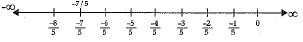
Q.17. Find the value of k, if (x - 1) is a factor of p(x) = 4x3 + 3x2 - 4x + k.
Ans. Since (x - 1) is a factor of p(x) = 4x3 + 3x2 - 4x + k
∴ p(1) = 0
⇒ 4(1)3 + 3(1)2 - 4(1) + k = 0
⇒ 4 + 3 - 4 + k = 0
⇒ k = - 3
Q.18. Write the intercepts of line 2x - 3y = 7 on coordinate axes.
OR
Show that the line joining (2, - 3) and (- 5, 1) is parallel to the line joining (7, - 1) and (0, 3).
Ans. The line is 2x - 3y = 7
Dividing both sides by 7, we have which is in intercept form x/a + y/b = 1
which is in intercept form x/a + y/b = 1
On comparing, we get
Intercept on x-axis a = 7/2 and intercept on y-axis b = -7/3
OR
Let m1 be the slope of the line joining (2, - 3) and (- 5, 1).
⇒ 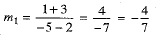
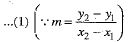
Also, let m2 be the slope of the line joining (7, - 1) and (0, 3).
⇒ 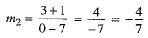 ...(2)
...(2)
From (1) and (2), we get
⇒ m1 = m2
⇒ The given lines are parallel.
Q.19. Find the value of k for which the point (1,-2) lies on the graph of the linear equation x - 2 y + k = 0.
Ans. Since, (1, - 2 ) lies on the graph of the linear equation x - 2 y + k = 0.
∴ 1 - 2(-2) + k = 0
⇒ 1 + 4+ k = 0
⇒ k + 5 = 0 ⇒ k = -5
Q.20. Explain when a system of axioms is called consistent.
Ans. A system of axioms is called consistent, when it is impossible to deduce from these axioms, a statement that contradicts any axiom or previously proved statement.
SECTION - B
Question numbers 21 to 26 carry 2 marks each.
Q.21. Represent 3.765 on the number line.
Ans. Suppose we want to locate 3.765 on the number line. As it lies between 3 arid 4. So let us look at the portion of the number line between 3 and 4. Suppose we divide this into 10 equal parts and mark each point of division as shown in figure. Then, the first mark to the right of 3 will represent 3.1 and second 3.2 and so on. Now, 3.765 lies between 3.7 and 3.8. We divide the distance between 3.7 and 3.8 into 10 equal parts.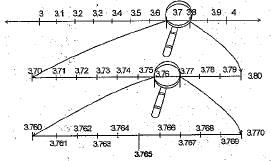
3.76 will be on the right of 3.7 at the sixth mark, and 3.77 will be on the right of 3.7 at the seventh mark and 3.765 will lie between 3.76 and 3,77 and so on. To mark 3.765, we have to use magnifying glass.
Q.22. Prove that: (cos x - cos y)2 + (sin x - sin y)2 = 4 sin2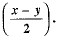
Ans. We have
L.H.S. = (cos x - cos y)2 + (sin x - sin y)2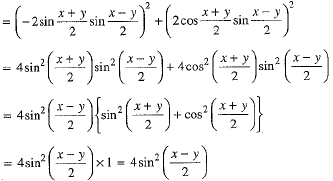
= R.H.S.
Q.23. In economy of any country, women are as equally important as men. As almost 40% population of any country is women, so they should also given chance to work and to help in improving the economy. (i) Compute the probability of a having 2 girls.
The department of health and family welfare of Government of NCR of Delhi collect data related to ratio between male and female children in families.
1500 families with 2 children each were selected randomly and the following data were recorded.
(i) Compute the probability of a family having 2 girls.
(ii) Compute the probability of a family having 0 girls.
(i) Compute the probability of a family having at least 1 girl.
Ans. (i) Number of family having 2 girls = 800
∴ P (having 2 girls) = 800/1500 = 8/15
(ii) Number of family having 0 girls = 200
∴ P (having 0 girls) = 200/1500 = 2/15
(iii) Number of families having atleast 1 girl, i.e.
Having 1 and 2 girls = 500 + 800 = 1300
∴ P (having atleast 1 girls) = 1300/1500 = 13/15
Q.24.
In figure ∠PQR = ∠PRQ then prove that ∠PQS = ∠PRT.
Ans. ∠PQR + ∠PQS = ∠PRQ + ∠PRT (Linear Pair)
∠PQR + ∠PQS = ∠PQR + ∠PRT (∵ ∠PQR = ∠PRQ)
∴ ∠PQS = ∠PRT Hence proved.
Q.25. Most numbers of people in India died or injured due to accidents as compared to any other country. An insurance company selected 2000 drivers at random (i.e., without any preference of one driver over another) in a particular city to find a relationship between age and accidents. The data obtained are given in the following table: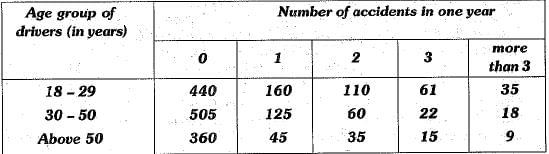
Find the probability of the following events for a driver selected at random from the city:
(i) being 18 - 29 years of age and having exactly 3 accidents in one year.
(ii) being 30 - 50 years of age and having one or more accidents in a year.
Ans. Here, total number of drivers = 2000
(i) The number of drivers in the age group 18 - 29 having exactly 3 accidents = 61.
So. P (driver in age group 18-29 having exactly 3 accidents in one year) = 61/2000 = 0.0305
(ii) The number of drivers in the age group 30 - 50 and having one or more than one accidents in one year = 125 + 60 + 22 + 18 = 225
P (driver in age group 30 - 50 having one or more accidents in one year) = 225/2000= 0.1125
Q.26. Without using distance formula, prove that the three points A(-2, 3, 5), 5(1, 2, 3) and C(7, 0, 1) are not collinear.
OR
Find the ratio in which yz-plane divides the line segment joining the points P(-2, 4, 7) and Q( 3, -5, 8).
Ans. Suppose the given points A, B and C are collinear and point C divides AB in the ratio k:1. Using the Section formula, the coordinates of point C are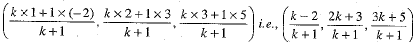
But. the point C is given to be (7, 0, 1)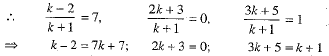
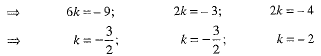
∴ From each of the equations, we do not get the same value.
Hence, the given points are not collinear.
OR
The given points are P(-2, 4, 7) and Q(3, - 5, 8).
Let the yz- plane divide the line joining P and Q in the ratio k : 1 at the point R.
The coordinates of the point R are 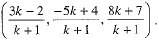 (using section formula)
(using section formula)
Since the point R lies on yz-plane, so x-coordinate of R = 0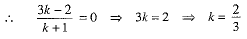
Required ratio is 2/3 : 1 i.e., 2:3.
Hence, yz-plane divides the line segment joining the given points in the ratio 2 : 3.
SECTION - C
Question 27 to 34 carry 3 marks each.
Q.27. Without actual division, prove that
2x4 - 5x3 + 2x2 - x + 2 is divisible by x2 - 3x + 2.
OR
If both x - 2 and x - 1/2 are factors of px2 + 5x + r, show that p = r.
Ans. Let p (x) = 2x4 - 5x3 + 2x2 - x + 2
and g(x) = x2 - 3x + 2
= ( x - 1 ) (x - 2)
If p(x) is divisible by g(x), then remainder becomes zero when 
Put x = 1, we have
p(1) = 2(1)4 - 5(1)3 + 2(1)2 - 1 + 2
= 2 - 5 + 2 - 1 + 2 = 0
Put x = 2, we have
p(2) = 2(2)4 - 5(2)3 + 2(2)2 - 2 + 2
= 32 - 40 + 8 - 2 + 2 - 0.
Hence, 2x4 - 5x3 + 2x2 - x + 2 is divisible by x2 - 3x + 2.
OR
Since x - 2 is a factor of px2 + 5x + r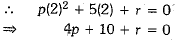
⇒ 4p + r = -10 ...(i)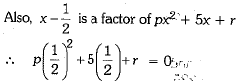
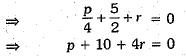
⇒ p + 4r = -10 ...(ii)
From (i) and (ii), we have
4p + r = p + 4r
⇒ 4p - p = 4 r - r
⇒ 3p = 3r
⇒ p = r
Q.28. Find the image of the point (3,8) with respect to the line x + 3y = 7 assuming the line to be a plane mirror.
OR
Find the equation of the ellipse satisfying the given condition:e = 3/4, foci on y -axis, centre at origin and passing through (6,4).
Ans. The equation of given line is x + 3y = 7 ...(1)
Let the given point be P(3, 8) and image of the point P(3, 8) in the line be Q(α, β).
The given line bisects the join of points P and Q, and is perpendicular to PQ.
Let R be the mid-point of PQ. So, the coordinates of R are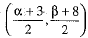
The point R lies on the line (1).
∴ 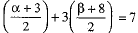
⇒ α + 3 + 3β + 24 =14
⇒ α + 3β + 13 =0 ...(2)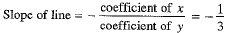
Slope of line segment PQ 
The line segment PQ is perpendicular to the line (1).
∴ (Slope of given line) x (Slope of PQ) = - 1
⇒ 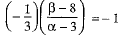
⇒ β - 8 = 3 ∝ - 9
⇒ 3α - β - 1 = 0 ...(3)
Multiplying (3) by 3, we get
9α -3β - 3 =0
Adding it to (2), we have
Putting the value of α in (2), we get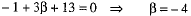
Hence, the image of point (3, 8) in the given line is (- 1, - 4).
OR
Since the foci is along the y-axis, therefore the equation of the ellipse is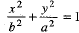 ...(1) (for a2>b2)
...(1) (for a2>b2)
If the ellipse (1) passes through (6, 4), then
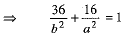 ...(2)
...(2)
We know that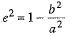
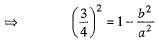
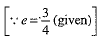
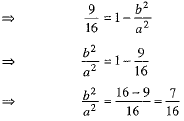
 ...(3)
...(3)
From (2) and (3), we get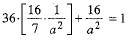
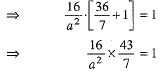
⇒ 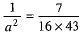 ...(4)
...(4)
From (3) and (4), we get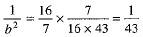 ...(5)
...(5)
Substituting the values of  from (4) and (5) in (1), we get
from (4) and (5) in (1), we get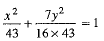
or 16x2 + 7y2 = 688.
as the required equation of the ellipse.
Q.29. In the given figure two circles whose centres O and O ' intersect at P. Through P, a line parallel to OO' intersecting the circles at C and D is drawn as shown. Prove that CD = 200'.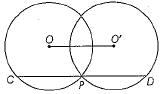
The given figure, if O is the circumcentre of a ΔABC and OD⊥BC, then prove that ∠BOD = ∠BAC.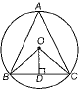
Ans. Given, circles having centres O and O 'intersect at P. Also, CD || OO'.
To prove CD = 2OO'
Construction Draw OA and O'B perpendicular to CD from O and O', respectively.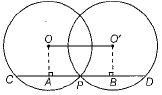
Proof OA⊥CD
∴ OA bisects the chord.
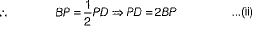

∴ CD = 2AB = 2OO' Hence proved.
Or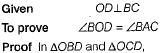


∴ ΔOBD ≌ ΔOCD [RHS rule]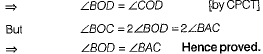
Q.30. Show that the diagonals of a rhombus are perpendicular to each other.
Ans. Let ABCD be the rhombus and AC and BD be the diagonal which intersect at point O.
In ΔAOD and ΔCOD
OA = OC
(diagonal of rhombus bisect each other)
OD = OD (Common)
AD = CD (Sides of rhombus)
∴ 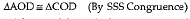
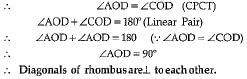
Q.31. ABCD is a parallelogram and AP and CQ are perpendiculars from vertices A and C on diagonal BD (see fig.). Show that: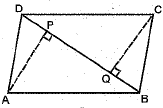
(i) ΔAPB ≌ ΔCQD
(ii) AP = CQ
OR
In the figure ΔPQR, PS and RT are medians and SM || RT. Prove that QM = 1/4 PQ.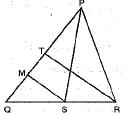
Ans. Given: In ||gm ABCD, AP and CQ are perpendiculars from the vertices A and C on the diagonal BD.
To Prove: (i) ΔAPB ≌ ΔCQD
(ii) AP = CQ
Proof: (i) In ΔAPB and ΔCQD
AB = DC [opp. sides of a ||gm ABCD]
∠APB = ∠DQC [each = 90°]
∠ABP = ∠CDQ [alt int. ∠s]
⇒ 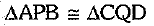 [by AAS congruence axiom]
[by AAS congruence axiom]
(ii) AP = CQ [c.p.c.t.]
Or
∵ PS is a median meeting QR at S.
∴ S is the mid-point of QR and SM || RT.
∴ By converse of mid-point theorem,
M is the mid-point of QT
∴ QM = 1/2 QT ...(i)
∵ RT is the median meeting PQ at T
∴  ...(ii)
...(ii)
From (i) and (ii), we have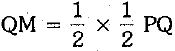 ⇒ QM
⇒ QM 
Q.32. Prove by using the principle of mathematical induction for all n ∈ N: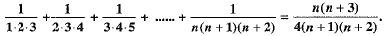
Ans. Let P(n) be the statement given by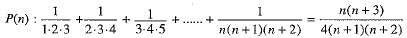
Step 1. For n = 1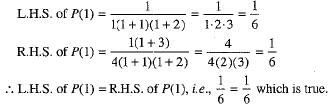
Thus, P(n) is true for n = 1.
Step 2. Assume that P(k) is true for some natural number k,
i.e.,  ...(1)
...(1)
Step 3. We shall now show that P(k + 1) is true whenever P(k) is true. For this we shall show that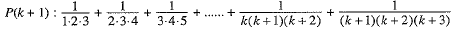
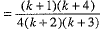
We have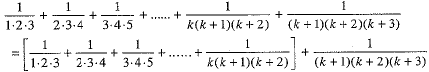
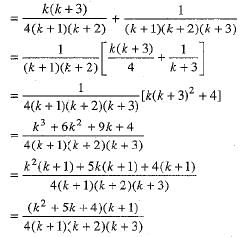
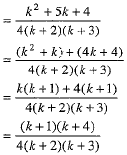
Thus, P(k + 1) is true whenever P(k) is true.
Hence, by the principle of mathematical induction P(n) is true for all natural numbers.
Q.33. From the given figure,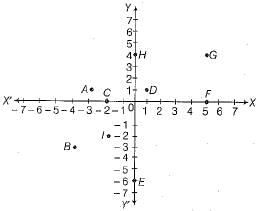
write
(i) the ordinate of the points A and C.
(ii) the point identified by the coordinates (1, 1).
(iii) the perpendicular distance of the point G from the X-axis.
(iv) the coordinates of the points B and F.
(v) the perpendicular distance of the point I from the Y-axis.
(vi) the points whose perpendicular distance from Y-axis is 2 units.
Ans. (i) Coordinates of points A and C are (-3, 1) and (-2, 0), respectively. Hence, ordinate of points A and C are 1 and 0.
(ii) (1, 1) represents the point D.
(iii) Coordinates of point G is (5, 4).
Hence, the perpendicular distance of the point G from the X-axis is 5 units.
(iv) Coordinates of points B and F are (-4, -3) and (5, 0) respectively.
(v) Coordinates of point I is (-2, -2).
Hence, the perpendicular distance of the point I from the Y-axis is -2 units.
(vi) There are two points C and I whose distance from Y-axis is 2 units.
Q.34. A dice is thrown thrice. Find the probability of getting
(i) 3 heads
(ii) Exactly 1 head
(iii) At least 2 heads
Ans. (i) P(2 girls) = 475/1500 = 19/60
(ii) P(1 girl) = 814/1500 = 407/750
(iii) P(no girl) = 211/1500
SECTION - D
Questions 35 to 40 carry 4 marks each
Q.35. Find the values of a and b in the following: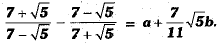
OR
Show that: 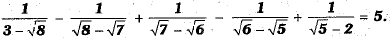
Ans. 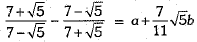
⇒ 
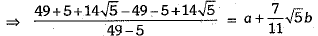
⇒ 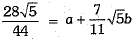
⇒ 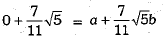
On comparing, we have a = 0 and b = 1.
OR
Rationalising the denominator of each term on L.H.S., we obtain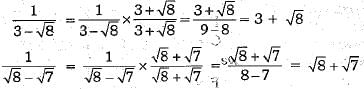
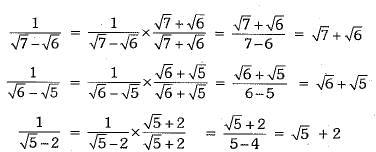
Now,
Q.36. If sinθ + sinφ = √3 (cos φ - cos θ), prove that sin 3θ + sin 3φ = 0.
OR
Solve : cot θ + cosec θ = √3
Ans. Given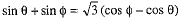
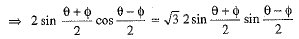
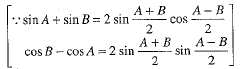
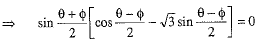
⇒ 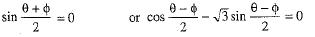
⇒ 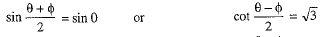
⇒ 
⇒ 
⇒ 
⇒ 
⇒ 
⇒ 
⇒ 
⇒ 
⇒ 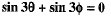
OR
The given equation is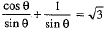
⇒ cos θ + 1 = √3 sinθ
⇒ √3 sinθ - cosθ = 1
Dividing both sides by 2, we get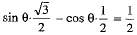
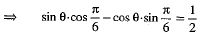
⇒ 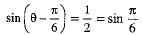
Then the general value of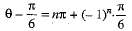
⇒ 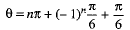
If n is even, i.e., n = 2m, then(-1)n = (-1)2m = 1
and 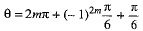
⇒ 
⇒ 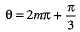
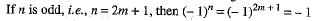
and 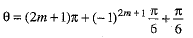
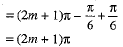
But sinθ= sin (2m + 1)π = 0 and cosec θ → ∞, which is undefined.
As such θ = (2m + 1)π is not acceptable.
∴ The general solution is
Q.37. If ax = cq = b and cy - az = d, then prove that xy = qz.
OR
If 52x - 1 -25x - 1 =2500, then find the value of x.
Ans. Given, ax = cq = b
Then, ax = b
⇒ a = b1/x ...(i)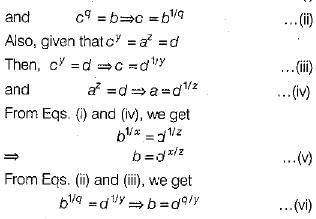
From Eqs. (v) and (vi), we get
dx/z = dq/y
On comparing the powers, we get
Or
We have, 52x - 1 - (52)x - 1 =2500
∴ 2x = 6 ⇒ x = 3 [comparing powers both sides]
Q.38. Construct ΔABC with BC = 4 cm, ∠B=75° and AB + AC = 10 cm.
Ans. Step of Construction:
(i) Draw a line segment BC = 4 cm.
(ii) Draw a ray BX such that ∠CBX = 75°
(iii) From ray BX, cut off BM = 10 cm.
(iv) Join MC.
(v) Draw perpendicular bisector on MC, which intersect BM at A.
(vi) Join AC, then ΔABC is the required triangle.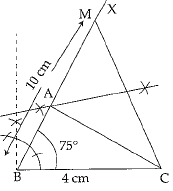
Q.39. A cylindrical pipe empties a spherical tank, full of water, at the rate of 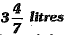 per second. How much time will it take to empty half of the tank, if radius of the tank is 3 m?
per second. How much time will it take to empty half of the tank, if radius of the tank is 3 m?
OR
The radius of a sphere is 14 cm. If the radius is increased by 50%, find by how much per cent its volume is increased.
Ans. Here, radius of the tank = 3 m
∴ Volume of the tank 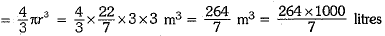
Now, water taken out in one second 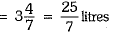
Volume of half of the tank 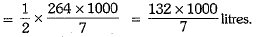
Thus, 132000/7 litres of water will be emptied by the cylindrical pipe in 
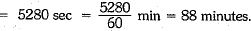
Or
Here, the radius of sphere (r) = 14 cm
∴ Volume of the sphere 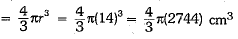
Now, radius is increased by 50%
∴ New radius of sphere = 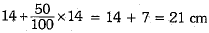
∴ New volume of sphere so formed = 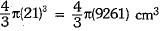
Thus, total increase in volume = 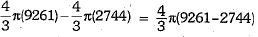
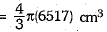
Hence, percent increase in volume = 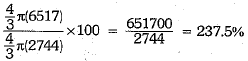
Q.40. Find the number of words with or without meaning which can be made using all the letters of the word AGAIN. If these words are written as in a dictionary, what will be the 50th word?
Ans. The number of words which can be made using all the letters of the word AGAIN.
In dictionary, the words at each stage are arranged in alphabetical order.
Starting with the letter A, the first word is AAGIN, the second word is AAGNI and so on. In other words, starting with the letter A, and arranging the remaining four letters GAIN, there are 4! = 24 words.
Thus, there are 24 words which starts with A.
Now, start with the letter G and arranging the remaining four letters A, A, I, N in different ways, we obtain
Thus, there are 12 words which start with G. Further, start with the letter I, and arranging the remaining four letters A, G, A, N in different ways, we obtain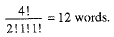
Thus, there are 12 words which start with I. Thus, we have so far constructed 48(= 2 4 + 1 2 + 1 2 ) words. The 49th word is NAAGI.
The 50th word is NAAIG.


















