NEET Previous Year Questions (2014-2024): Motion in a Straight Line | Physics Class 11 PDF Download
2024
Q1: The velocity (v)− time (t) plot of the motion of a body is shown below: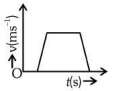 The acceleration (a)− time (t) graph that best suits this motion is : [2024]
The acceleration (a)− time (t) graph that best suits this motion is : [2024]
(a) 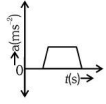
(b) 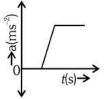
(c) 
(d) 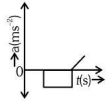
Ans: (c)
Initially, the body has zero velocity and zero slope. Hence the acceleration would be zero initially. After that, the slope of v-t curve is constant and positive.
After some time, velocity becomes constant and acceleration is zero.
After that, the slope of v-t curve is constant and negative.
2023
Q1: The position of a particle is given by
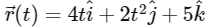
where t is in seconds and r in metre. Find the magnitude and direction of velocity v(t), at t = 1 s, with respect to x-axis
Ans: (a)
Q2: A vehicle travels half the distance with speed v and the remaining distance with speed 2v. Its average speed is [2023]
(a) V/3
(b) 2V/3
(c) 4V/3
(d) 3V/4
Ans: (c)
Solution: 
Q3: A bullet from a gun is fired on a rectangular wooden block with velocity u. When bullet travels 24 cm through the block along its length horizontally, velocity of bullet becomes u/3. Then it further penetrates into the block in the same direction before coming to rest exactly at the other end of the block. The total length of the block is [2023]
(a) 27 cm
(b) 24 cm
(c) 28 cm
(d) 30 cm
Ans: (a)
Solution: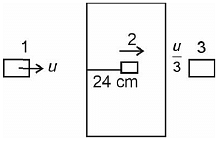
between 1 to 2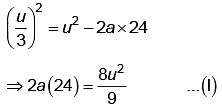
between 2 to 3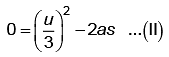
From equation (I) and (II)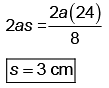
Length of wooden block is 24 + 3 = 27 cm
Q4: A horizontal bridge is built across a river. A student standing on the bridge throws a small ball vertically upwards with a velocity 4 m s–1. The ball strikes the water surface after 4 s. The height of bridge above water surface is (Take g = 10 m s–2) [2023]
(a) 56 m
(b) 60 m
(c) 64 m
(d) 68 m
Ans: (c)
Solution: 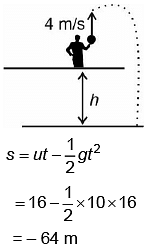
Height of bridge above water surface = 64 m
2022
Q1: The position-time (x - t) graph for positive acceleration is
(a) 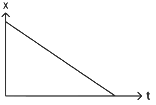
(b) 
(c) 
(d) 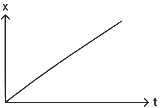
Ans: (b)
Slope of position-time (x - t) graph represents velocity.
In graph-2, the slope is increasing hence the velocity is increasing hence acceleration is positive.
Q2: The ratio of the distances travelled by a freely falling body in the 1st, 2nd, 3rd, and 4th second [2022]
(a) 1 : 4 : 9 : 16
(b) 1 : 3 : 5 : 7
(c) 1 : 1 : 1 : 1
(d) 1 : 2 : 3 : 4
Ans: (b)
Solution: 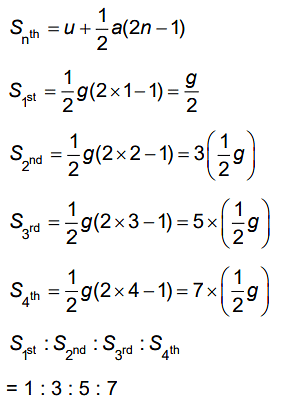
Q3: The displacement-time graphs of two moving particles make angles of 30° and 45° with the x-axis as shown in the figure. The ratio of their respective velocity is [2022]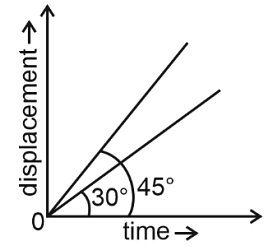 (a) 1 : 1
(a) 1 : 1
(b) 1 : 2
(c) 1: √3
(d) √3 : 1
Ans: (c)
Solution:
Slope of x-t curves gives the velocity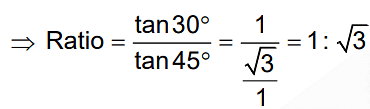
2021
Q1: A small block slides down on a smooth inclined plane starting from rest at time t=0. Let Sn be the distance travelled by the block in the interval t= n-1 to t=n. Then the ratio 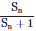 is: [2021]
is: [2021]
(a) 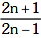
(b) 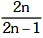
(c) 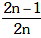
(d) 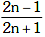
Ans: (d)
Solution:
Sn = Distance in nth sec.
i.e. t = n – 1 to t = n
Sn + 1 = Distance in (n + 1)th sec.
i.e. t = n to t = n + 1
So as we know,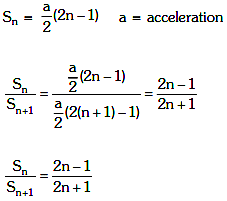
2020
Q1: A ball is thrown vertically downward with a velocity of 20m/s from the top of a tower. It hits the ground after some time with a velocity of 80m/s. The height of the tower is : (g = 10m/s2) [2020]
(a) 320 m
(b) 300 m
(c) 360 m
(d) 340 m
Ans: (b)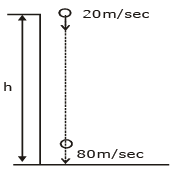
v2 – u2 = 2as
(80)2 – (–20)2 = 2(–10) × s
6400 – 400 = 2 × (–10) × s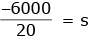
s = – 300 m
Height of tower h = 300 m
2019
Q1: The speed of a swimmer in still water is 20 m/s. The speed of river water is 10 m/s and is flowing due east. If he is standing on the south bank and wishes to cross the river along the shortest path, the angle at which he should make his strokes w.r.t. north is given by :
(a) 0o
(b) 60
(c) 45o west
(d) 30o west
Ans: (d)

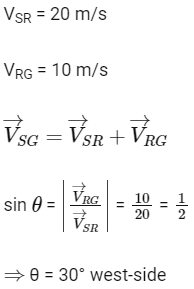
2017
Q1: Preeti reached the metro station and found that the escalator was not working. She walked up the stationary escalator in time t1. On other days, if she remains stationary on the moving escalator, then the escalator takes her up in time t2. The time taken by her to walk up on the moving escalator will be [2017]
(a) 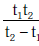
(b) 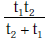
(c) t1 – t2
(d) 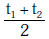
Ans: (b)
Solution:
As we learnt in
Case of Relative velocity -
When A & B are moving along with straight line in opposite direction.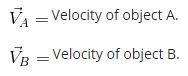
Relative velocity of A with respect to B is.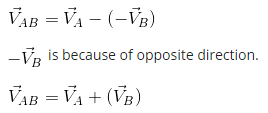
2016
Q1: Two cars P and Q start from a point at the same time in a straight line and their positions are represented by
xP(t) = (at + bt2) and xQ(t) = (ft
At what time do the cars have the same velocity ? [2016]
(a) 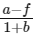
(b) 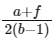
(c) 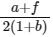
(d) 
Ans: (d)
For car P,

Similarly for car Q,

When they have same velocity then, vP(t) = vQ(t)
a + 2bt = f - 2t
⇒ 2t(b + 1) = f - a
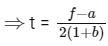
Q2: A particle moves so that its position vector is given by r = cosωtx + sinωty. Where ω is a constant. Which of the following is true?
(a) Velocity is perpendicular to r and acceleration is directed away from the origin.
(b) Velocity and acceleration both are perpendicular to r
(c) Velocity is acceleration both are parallel to r
(d) Velocity is perpendicular to r and acceleration is directed towards the origin. [2016]
Ans: (d)
Solution: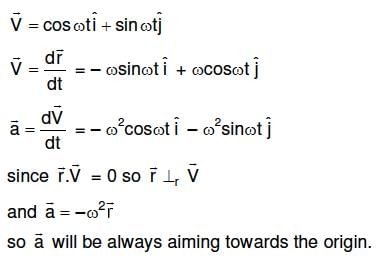
Q3: If the velocity of a particle is  , where A and B are constants, then the distance travelled by it between 1s and 2s is [2016]
, where A and B are constants, then the distance travelled by it between 1s and 2s is [2016]
(a) A/2 + B/3
(b) 3A/2 + B
(c) 3A + 7B
(d) 3A/2 + 7B/3
Ans: (d)
Solution:
2015
Q1: A particle of unit mass undergoes one-dimensional motion such that its velocity varies according to v(x) = βx-2n, where β and n are constants and x is the position of the particle. The acceleration of the particle as a function of x, is given by :
[NEET / AIPMT 2015 Cancelled Paper ]
(a) -2nβ2 e-4n + 1
(b) -2nβ2 x-2n - 1
(c) -2nβ2 x-4n - 1
(d) -2nβ2 x-2n + 1
Ans: (c)
Solution: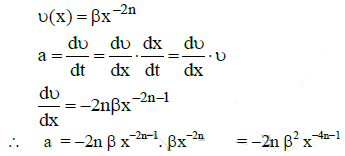
|
97 videos|378 docs|103 tests
|
FAQs on NEET Previous Year Questions (2014-2024): Motion in a Straight Line - Physics Class 11
| 1. What is the equation for motion in a straight line? |  |
| 2. How is velocity related to displacement in motion in a straight line? |  |
| 3. What is the difference between speed and velocity in motion in a straight line? |  |
| 4. How does acceleration affect motion in a straight line? |  |
| 5. What are the different types of motion in a straight line? |  |

|
Explore Courses for NEET exam
|

|


















