NEET Previous Year Questions (2015-2024): Laws of Motion | Physics Class 11 PDF Download
The Laws of Motionis an important chapter in NEET Physics. It is a fundamental concept that forms the basis for understanding many other topics in Physics. Let's have a look at Previous Year Questionsof the chapter:
2024
Q1: A horizontal force 10 N is applied to a block A as shown in figure. The mass of blocks A and B are 2kg and 3kg respectively. The blocks slide over a frictionless surface. The force exerted by block A on block B is : [2024]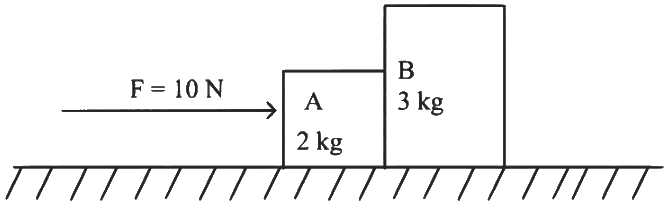 (a) Zero
(a) Zero(b) 4 N
(c) 6 N
(d) 10 N
 View Answer
View AnswerAns:(c)
Find the total mass of the system:
mtotal= mA + mB = 2 kg + 3 kg = 5kg
Calculate the acceleration of the system: Since both blocks move together on a frictionless surface, they will have the same acceleration. Using Newton's second law:
Ftotal = mtotal ⋅ a
10N = 5kg ⋅ a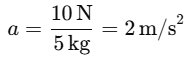 Find the force exerted by block A on block B: Block B is being accelerated by the force exerted by block A. The force on block B can be calculated using Newton’s second law again, but this time for block B alone:
Find the force exerted by block A on block B: Block B is being accelerated by the force exerted by block A. The force on block B can be calculated using Newton’s second law again, but this time for block B alone:
Fon B = mB ⋅a
F on B = 3kg ⋅ 2m/s2 = 6 N
Thus, the force exerted by block A on block B is 6 N.
2023
Q1: A football player is moving southward and suddenly turns eastward with the same speed to avoid an opponent. The force that acts on the player while turning is [2023]
(a) Along eastward
(b) Along northward
(c) Along north-east
(d) Along south-west
 View Answer
View AnswerAns: (c)
Problem Breakdown:
- The football player is initially moving southward and then suddenly turns eastward while maintaining the same speed.
- The question asks about the direction of the force acting on the player while turning.
Concept:
- Centripetal Force: When an object changes direction, there is a force directed towards the center of the circular path, which is called centripetal force.
- The player is changing direction, meaning their velocity vector is also changing direction. In this case, the player is turning from south to east, which implies a change in velocity towards the east.
Force Direction:
- The force responsible for this change in direction would act towards the north-east because the player is transitioning between the southward and eastward directions. The force is responsible for changing both the magnitude and direction of the velocity as the player turns.
Thus, the force acts along the north-east direction.
Q2: Calculate the maximum acceleration of a moving car so that a body lying on the floor of the car remains stationary. The coefficient of static friction between the body and the floor is 0.15 ( g = 10 m s–2). [2023]
(a) 1.2 m s–2
(b) 150 m s–2
(c) 1.5 m s–2
(d) 50 m s–2
 View Answer
View AnswerAns: (c)
Problem Breakdown:
We need to calculate the maximum acceleration of a moving car such that a body lying on the floor of the car remains stationary. Given:
- Coefficient of static friction (μ) = 0.15
- Acceleration due to gravity (g) = 10 m/s²
Concept:
For the body to remain stationary relative to the car, the maximum static friction force must equal the force required to accelerate the body along with the car. The friction force is what keeps the body stationary relative to the moving car.
Static friction force:
Ffriction = μ⋅N
Where N is the normal force, and for a horizontal surface, N = m ⋅ g.
Therefore:
Ffriction = μ ⋅ m ⋅ g
Force required for acceleration:The force required to accelerate the body is:
F = m ⋅a
For the maximum acceleration, the static friction force must equal the force required for acceleration:
μ ⋅ m ⋅g = m⋅a
Simplifying the equation (the mass 𝑚 m cancels out):
a = μ ⋅ g
Substitute the values:
a = 0.15 ⋅ 10 m/s2
a = 1.5 m/s2
Thus, the maximum acceleration of the car is 1.5 m/s².
Q3:A bullet from a gun is fired on a rectangular wooden block with velocity u. When bullet travels 24 cm through the block along its length horizontally, velocity of bullet becomes u/3. Then it further penetrates into the block in the same direction before coming to rest exactly at the other end of the block. The total length of the block is:[2023]
(a) 24 cm
(b) 28 cm
(c) 33 cm
(d) 27 cm
 View Answer
View AnswerAns:(d)
To solve the problem step by step, we will analyze the motion of the bullet as it penetrates the wooden block.
Step 1: Understand the motion of the bullet
The bullet is fired with an initial velocity u and travels through the block. After penetrating 24 cm, its velocity reduces to u/3 It then continues to penetrate until it comes to rest.
Step 2: Use the first part of the motion
We can apply the equation of motion to the first part of the bullet's journey through the block. The equation we will use is:
v2=u2+2as
Where:- v = final velocity after penetrating 24 cm = u/3
- u = initial velocity = u
- a = acceleration (deceleration in this case, so it will be negative)
- s = distance traveled = 24 cm = 0.24 m
Substituting the known values into the equation: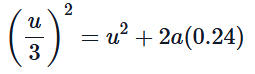 This simplifies to:
This simplifies to: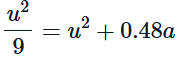 Rearranging gives:
Rearranging gives: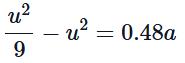
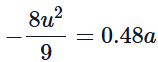 Thus,
Thus,
a = - 8 u2 / 9 × 0.48 = - 8 u2 / 4.32 = - 1.85 u2
Step 3: Use the second part of the motion
Now, the bullet continues to penetrate until it comes to rest. The initial velocity for this part is u/3 nd the final velocity is 0. We will again use the equation of motion: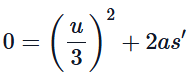 Where s′ is the additional distance traveled before coming to rest. Substituting the values:
Where s′ is the additional distance traveled before coming to rest. Substituting the values:
0 = u2 / 9 + 2 ( -1.85 u2) s'
This simplifies to:s' = 1/ 9 × 3.7 = 0.03 m = 3 cm
Step 4: Calculate the total length of the block
The total length of the block is the sum of the distances:
Total Length = 24 cm + 3cm = 27cm
2022
Q1: If 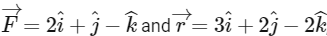
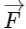 and
and 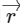 have the magnitudes respectively as [2022]
have the magnitudes respectively as [2022]
(a) 10, 2
(b) 5, √3
(c) 4, √5
(d) 10, √2
 View Answer
View AnswerAns:(d)
Given: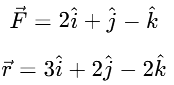 1. Scalar Product (Dot Product):
1. Scalar Product (Dot Product):
The dot product of two vectors 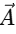 and
and 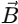 is given by:
is given by: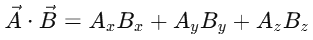 Substitute the components of
Substitute the components of 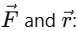
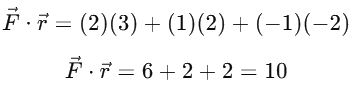
So, the scalar product is 10.
2. Vector Product (Cross Product):
The cross product of two vectors  is given by the determinant of the following matrix:
is given by the determinant of the following matrix: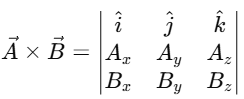 Substitute the components of
Substitute the components of 
Now, calculate the determinant: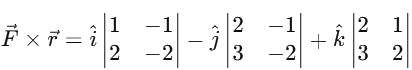
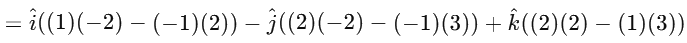
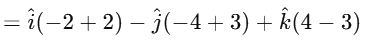
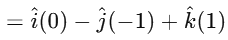
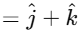
The vector product is 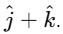
Magnitude of the Vector Product:
The magnitude of 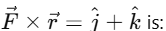
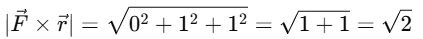
Thus, the correct answer is: (d) 10, √2
Q2: In the diagram shown, the normal reaction force between 2 kg and 1 kg is (Consider the surface, to be smooth) : (Given g = 10 ms−2) [2022]
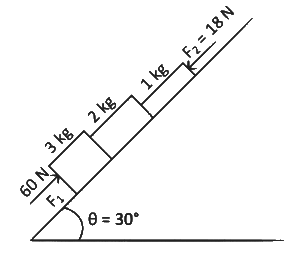
(a) 10 N
(b) 25N
(c) 39 N
(d) 6 N
Ans: (b)
 View Answer
View AnswerQ3: An electric lift with a maximum load of 2000 kg (lift + passengers) is moving up with a constant speed of 1.5 ms–1. The frictional force opposing the motion is 3000 N. The minimum power delivered by the motor to the lift in watts is : (g = 10 m s–2 ) [2022]
(a) 20000
(b) 34500
(c) 23500
(d) 23000
 View Answer
View AnswerAns:(b)
Solution:
Given:
Maximum load (lift + passengers) = 2000 kg
Constant speed v=1.5m/s
Frictional force f = 3000N
Gravitational acceleration g = 10m/s2
Step-by-Step:
Calculate the force required to lift the load: The force required to lift the load at a constant speed is equal to the gravitational force acting on the lift: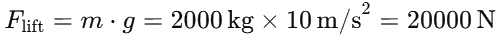
Total force acting on the lift: The total force the motor must overcome includes both the gravitational force and the frictional force: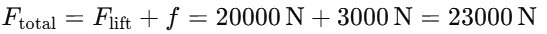
Calculate the power: Power is given by the product of force and velocity: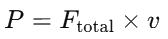 Substituting the values:
Substituting the values:
P = 23000N × 1.5m/s = 34500W
Thus, the minimum power delivered by the motor to the lift is 34500 W.
2021
Q1: A ball of mass 0.15 kg is dropped from a height 10 m, strikes the ground and rebounds to the same height. The magnitude of impulse imparted to the ball is (g = 10 m/s2) nearly : [2021]
(a) 2.1 kg m/s
(b) 1.4 kg m/s
(c) 0 kg m/s
(d) 4.2 kg m/s
 View Answer
View AnswerAns:(d)
Solution:
Given:
Mass of the ball, m = 0.15kg
Initial height, h = 10m
Gravitational acceleration, g = 10m/s2
Velocity just before impact: The ball falls from a height of 10 meters, and we can use the kinematic equation to calculate the velocity just before it hits the ground: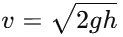
Substituting the values: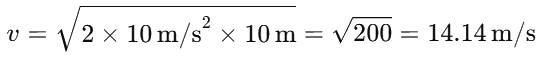
This is the velocity just before hitting the ground (downward).
Velocity after rebounding: Since the ball rebounds to the same height, the velocity after rebounding is also 14.14 m/s, but in the opposite direction (upward).
Change in velocity: The change in velocity Δv is the difference between the final velocity and the initial velocity: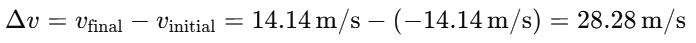
Impulse: Impulse J is the change in momentum, which is given by:
J = m ⋅ Δv
Substituting the values:
J = 0.15kg × 28.28m/s = 4.242 kg⋅m/s
2020
Q1: Two bodies of mass 4 kg and 6 kg are tied to the ends of a massless string. The string passes over a pulley which is frictionless (see figure). The acceleration of the system in terms of acceleration due to gravity (g) is : [2020]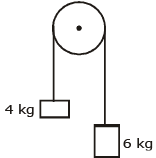
(a) g/5
(b) g/10
(c) g
(d) g/2
 View Answer
View AnswerAns: (a)
Solution:
1. Identify the forces acting on the masses:
- For the 4 kg mass (m1): The force acting on it is F1 = m1g.
- For the 6 kg mass (m2): The force acting on it is F2 = m2g.
2. Calculate the net force: The net force acting on the system is due to the difference in the weights of the two masses. The heavier mass (6 kg) will pull the lighter one (4 kg) upwards while it descends.
Fnet = m2g − m1g = (6g − 4g) = 2g
3. Total mass of the system: The total mass of the system is the sum of the masses of both bodies:
Mtotal = m1 + m2 = 4 kg + 6 kg = 10 kg
4. Calculate the acceleration: Using Newton’s second law, the net force is related to the total mass and the acceleration of the system:
Fnet = Mtotal ⋅ a
Substituting the values:
2g = 10a
Solving for a: 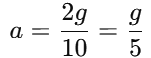
2019
Q1: A block of mass 10 kg is in contact against the inner wall of a hollow cylindrical drum of radius 1 m. The coefficient of friction between the block and the inner wall of the cylinder is 0.1. The minimum angular velocity needed for the cylinder to keep the block stationary when the cylinder is vertical and rotating about its axis, will be : (g 10 m/s2) [2019]
(a) √10 rad/s
(b) 10/2π rad/s
(c) 10 rad/s
(d) 10π rad/s
 View Answer
View AnswerAns:(c)
Solution:
Concept: For the block to remain stationary, the frictional force must balance the gravitational force. The frictional force is provided by the normal force, which in this case is the centrifugal force due to the rotation of the drum.
1. Gravitational Force (Downward): The gravitational force acting on the block is:
Fgravity = mg = 10 kg × 10 m/s2 = 100N
2. Frictional Force (Upward): The frictional force must balance the gravitational force:
Ffriction = μ N
Where N is the normal force, which is the centrifugal force in this case.
3. Centrifugal Force: The centrifugal force acting on the block due to the rotation is:
N = mω2r
Where ω is the angular velocity, and r is the radius of the cylinder.
4. Balance of Forces: For the block to remain stationary, the frictional force must balance the gravitational force:
Ffriction = Fgravity
Substituting the expressions:
μN = mg
μ(mω2r)=mg
Simplifying:
μω2r=g
Solving for ω: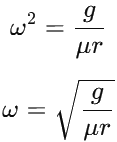
Substitute the Values: Substituting g = 10m/s2, μ=0.1, and r = 1m: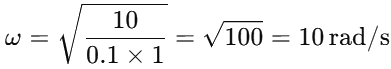
Q2: A mass m is attached to a thin wire and whirled in a vertical circle. The wire is most likely to break when: [2019]
(a) The mass is at the highest point
(b) The wire is horizontal
(c) The mass is at the lowest point
(d) Inclined at an angle of 60° from vertical
 View Answer
View AnswerAns: (c)
Concept: The tension in the wire is responsible for keeping the mass moving in a circular path. At different points in the circle, the forces on the mass vary due to the direction of gravity. The wire will break when the tension in the wire is at its maximum.
At the highest point:
- The forces acting are the tension in the wire Ttop and the weight of the mass mg, both acting downward.
- The net force provides the centripetal force to keep the mass moving in a circle.
- The tension is given by:


Comparison:
- At the highest point, the tension is lower because gravity acts in the same direction as the centripetal force, reducing the required tension.
- At the lowest point, the tension is greater because the wire must support the mass’s weight and provide the centripetal force. This is where the tension is maximum.
Since the wire is more likely to break at the point where the tension is highest, the wire is most likely to break when the mass is at the lowest point of the vertical circle.
Q3: When an object is shot from the bottom of a long smooth inclined plane kept at an angle 60° with horizontal, it can travel a distance x1 along the plane. But when the inclination is decreased to 30° and the same object is shot with the same velocity, it can travel x2 distance.
Then x1 : x2 will be: [2019]
(a) 1: √2
(b) √2: 1
(c) 1: √3
(d) 1: 2√3
 View Answer
View AnswerAns: (c)
Concept: The object is projected with the same initial velocity on two inclined planes.
The distances x1 and x2 are dependent on the components of velocity along and perpendicular to the inclined plane, as well as the effect of gravity along the plane.
1. Distance traveled on an inclined plane: The distance traveled by an object on an inclined plane is influenced by the acceleration due to gravity acting along the plane. The distance can be expressed using the kinematic equation for motion along an inclined plane: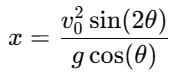 where:
where:
- v0 is the initial velocity,
- θ is the angle of inclination,
- g is the acceleration due to gravity.
2. For the first case (angle θ = 60∘):The distance x1 along the plane when the angle is 60° is given by: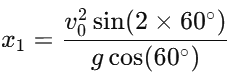
Simplifying the trigonometric values: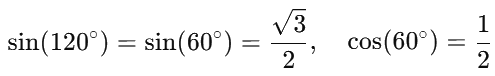
Thus: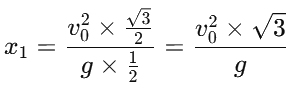 For the second case (angle θ = 30∘):The distance x2 along the plane when the angle is 30° is given by:
For the second case (angle θ = 30∘):The distance x2 along the plane when the angle is 30° is given by: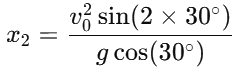 Simplifying the trigonometric values:
Simplifying the trigonometric values: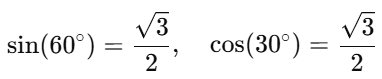 Thus:
Thus: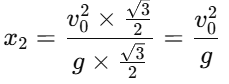 4. Finding the ratio x1 : x2 : Now, divide x1 by x2 :
4. Finding the ratio x1 : x2 : Now, divide x1 by x2 :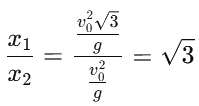 Therefore:
Therefore:
x1 : x2 = 1: √3
2018
Q1: Which one of the following statements is incorrect?
(a) Rolling friction is smaller than sliding friction
(b) Limiting value of static friction is directly proportional to normal reactions
(c) Frictional force opposes the relative motion
(d) Coefficient of sliding friction has dimensions of length [2018]
 View Answer
View AnswerAns: (d)
(a) Rolling friction is smaller than sliding friction:
This is a correct statement. Rolling friction is generally much smaller than sliding friction because the contact area in rolling is reduced, and there is less interlocking between surfaces compared to sliding.
(b) Limiting value of static friction is directly proportional to normal reaction:
This is also correct. The limiting value of static friction fs is given by: fs = μsN
where μ s is the coefficient of static friction and N is the normal reaction force. So, static friction is directly proportional to the normal force.
(c) Frictional force opposes the relative motion:
This is a correct statement. The frictional force always acts in the direction opposite to the relative motion or the attempted relative motion between two surfaces.
(d) Coefficient of sliding friction has dimensions of length:
This is incorrect. The coefficient of friction, whether static or sliding, is a dimensionless quantity. It is simply a ratio of the frictional force to the normal force and does not have any physical dimensions.
Q2: A block of mass m is placed on a smooth inclined wedge ABC of inclination θ as shown in the figure. The wedge is given an acceleration 'a' towards the right. The relation between a and θ for the block to remain stationary on the wedge is :- [2018]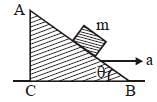
(a) 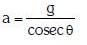
(b) 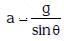
(c) a = g cos θ
(d) a = g tan θ
 View Answer
View AnswerAns: (d)
Key Considerations:
- The wedge is smooth, meaning no friction acts between the block and the wedge.
- The block must remain stationary relative to the wedge, implying the net force on the block must be directed perpendicular to the wedge surface.
Forces acting on the block:
- Gravitational force: The gravitational force acting on the block is mg, which acts vertically downward.
- Normal force: The normal force N acts perpendicular to the inclined plane.
- Pseudo force due to acceleration: Since the wedge is accelerating to the right with acceleration a, a pseudo force ma acts on the block towards the left (relative to the wedge), parallel to the incline.
Resolving forces:
- The gravitational force can be resolved into two components:
- Parallel to the inclined plane: mgsinθ
- Perpendicular to the inclined plane: mgcosθ
- The pseudo force ma acts parallel to the wedge, providing a component in the opposite direction along the incline.
For the block to remain stationary: The net force along the incline must be zero. This means the force component along the incline due to the pseudo force must balance the force component along the incline due to gravity:
ma cosθ=mg sinθ
Simplifying for a:
a = g tanθ
Thus, the relationship between the acceleration a of the wedge and the angle of inclination θ is: a = g tanθ
2017
Q1: Two blocks A and B of masses 3 m and m respectively are connected by a massless and inextensible string. The whole system is suspended by a massless spring as shown in figure. The magnitudes of acceleration of A and B immediately after the string is cut, are respectively : [2017]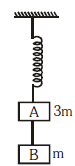
(a) 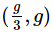
(b) g, g
(c) 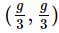
(d) 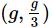
 View Answer
View Answer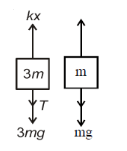
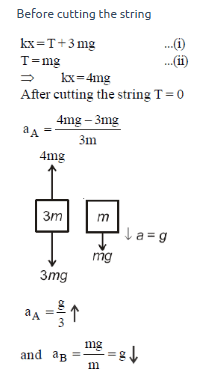
Q2: One end of string of length l is connected to a particle of mass 'm' and the other end is connected to a small peg on a smooth horizontal table. If the particle moves in circle with speed 'v', the net force on the particle (directed towards centre) will be (T represents the tension in the string) [2017]
(a) 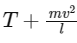
(b) 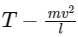
(c) zero
(d) T
 View Answer
View AnswerAns: (d)
Key Concepts:
- When an object moves in a circular path, the net force directed towards the center (centripetal force) is responsible for keeping the object in circular motion.
- The centripetal force Fc required to keep a particle of mass 𝑚 m moving in a circle of radius l at a speed v is given by:
 This force is directed towards the center of the circle.
This force is directed towards the center of the circle. - Tension in the String: The tension in the string, T, provides the necessary centripetal force to keep the particle moving in a circular path.
- Net Force Towards the Center: The net force on the particle, which is directed towards the center, must account for both the tension in the string and the centripetal force. The tension in the string must balance the centripetal force entirely. Therefore, the tension in the string T equals the centripetal force mv2/l.
- Thus, the net force acting on the particle towards the center is: T = mv2/l
2016
Q1: A car is negotiating a curved road of radius R. The road is banked at an angle .. The coefficient of friction between the tyres of the care and the road is 1s. The maximum safe velocity on this road is: [2016]
(a) 
(b) 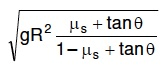
(c) 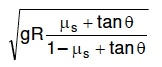
(d) 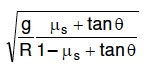
 View Answer
View AnswerA car is negotiating a curved road of radius R. The road is banked at angle straight theta and the coefficient of friction between the tyres of car and the road is straight mu subscript straight s.
The given situation is illustrated as:
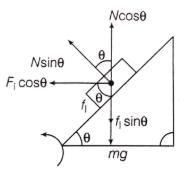
In the case of vertical equilibrium,
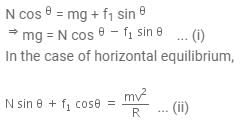
Dividing Eqns. (i) and (ii), we get
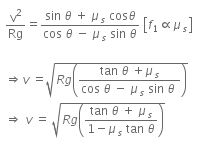
Q2: What is the minimum velocity with which a body of mass m must enter a vertical loop of radius R so that it can complete the loop ? [2016]
(a) √5gR
(b) √gR
(c) √2gR
(d) √3gR
 View Answer
View AnswerAns: (a)
The question is illustrated in the figure below,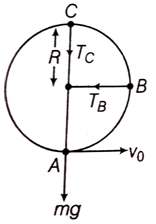
Let, the tension at point A be TA.
Using Newton's second law, we have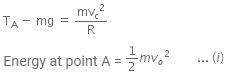
Energy at point C is,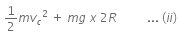
At point C, using Newton's second law,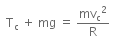
In order to complete a loop, Tc ≥ 0
so,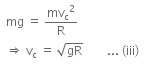
From equation (i) and (ii)
Using the principle of conservation of energy,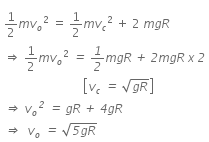
Q3: A particle of mass 10 g moves along a circle of radius 6.4 cm with a constant tangential acceleration. What is the magnitude of this acceleration if the kinetic energy of the particle becomes equal to 8 x 10-4J by the end of the second revolution after the beginning of the motion ? [2016]
(a) 0.2 m/s2
(b) 0.1 m/s2
(c) 0.15 m/s2
(d) 0.18 m/s2
 View Answer
View AnswerAns: (b)
Given, mass of particle. m = 0.01 kg
Radius of circle along which particle is moving , r = 6.4 cm
Kinetic energy of particle, K.E. = 8 x 10-4 J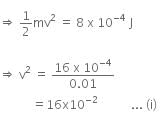
Given that, KE of particle is equal to 8 x 10-4 J by the end of second revolution after the beginning of the motion of particle.
It means, initial velocity (u) is 0 m/s at this moment.
Now, using the Newton's 3rd equation of motion,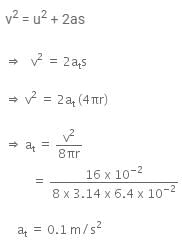
2015
Q1: Two stones of masses m and 2m are whirled in horizontal circles, the heavier one in a radius r/2 and the lighter one in radius r. The tangential speed of lighter stone is n times that of the value of heavier stone when they experience same centripetal forces. The value of n is [NEET / AIPMT 2015]
(a) 4
(b) 1
(c) 2
(d) 3
 View Answer
View AnswerAns: (c)
Given:
Mass of lighter stone = m, radius of its circular path = r.
Mass of heavier stone = 2m, radius of its circular path = r/2.
The centripetal forces on both stones are the same.
Let the tangential speed of the lighter stone be v1 and that of the heavier stone be v2.
1. Centripetal force formula:The centripetal force Fc acting on a body moving in a circular path is given by: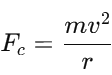 where:
where:
- m is the mass of the stone,
- v is the tangential speed,
- r is the radius of the circular path.
2. Centripetal force for the lighter stone:For the lighter stone of mass m and radius r, the centripetal force is: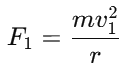
3. Centripetal force for the heavier stone:For the heavier stone of mass 2m and radius r/2, the centripetal force is: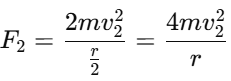 4. Setting the centripetal forces equal:Since both stones experience the same centripetal force:
4. Setting the centripetal forces equal:Since both stones experience the same centripetal force:
F1 = F2
Substituting the expressions for F1 and F2: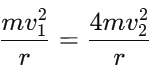 Simplifying:
Simplifying: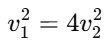 Taking the square root of both sides:
Taking the square root of both sides:
v1 = 2v2
Conclusion:
The tangential speed of the lighter stone is 2 times the tangential speed of the heavier stone. Thus, the value of n is 2.
|
97 videos|378 docs|103 tests
|
FAQs on NEET Previous Year Questions (2015-2024): Laws of Motion - Physics Class 11
| 1. What are the key concepts of the Laws of Motion that are frequently tested in NEET exams? |  |
| 2. How do I prepare effectively for the Laws of Motion section in the NEET exam? |  |
| 3. Can you explain Newton's second law of motion and its significance in the NEET syllabus? |  |
| 4. What types of problems related to Laws of Motion are commonly asked in NEET exams? |  |
| 5. Are there any important formulas related to the Laws of Motion that I should memorize for NEET? |  |

|
Explore Courses for NEET exam
|

|

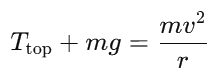
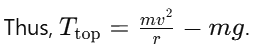
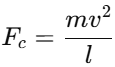 This force is directed towards the center of the circle.
This force is directed towards the center of the circle.

















