NEET Previous Year Questions (2014-2024): Electrostatics Potential & Capacitance | Physics Class 12 PDF Download
2024
Q1: Given below are two statements: one is labelled as Assertion A and the other is labelled as Reason R.Assertion A: The potential (V) at any axial point, at 2m distance (r) from the centre of the dipole of dipole moment vector
 of magnitude, 4 × 10−6Cm, is ±9 × 103V.
of magnitude, 4 × 10−6Cm, is ±9 × 103V.(Take 1 / 4πϵ0 = 9 × 109 SI units)
Reason R:
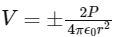 , where r is the distance of any axial point, situated at 2m from the centre of the dipole.
, where r is the distance of any axial point, situated at 2m from the centre of the dipole.In the light of the above statements, choose the correct answer from the options given below:
(a) Both A and R are true and R is the correct explanation of A.
(b) Both A and R are true and R is NOT the correct explanation of A.
(c) A is true but R is false.
(d) A is false but R is true. [2024]
Ans: (c)
The potential V at any point, at distance r from centre of dipole =
At axial point where
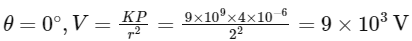
At axial point where
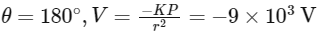
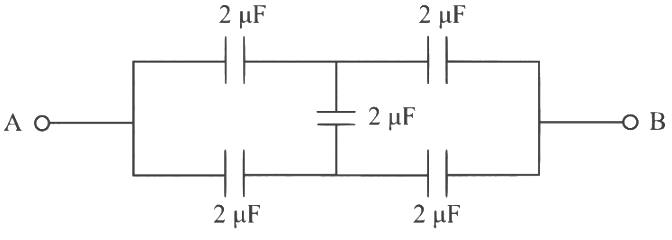 (a) 2 μF
(a) 2 μF
(b) 1 μF
(c) 0.5 μF
(d) 4 μF [2024]
Ans: (a)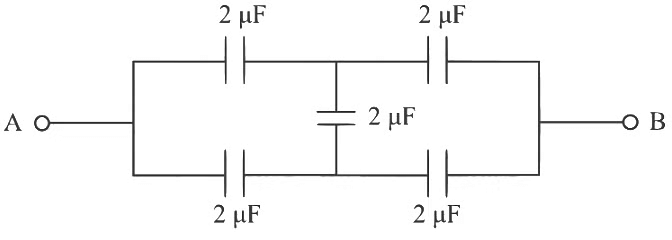 Given circuit is balanced Wheatstone bridge
Given circuit is balanced Wheatstone bridge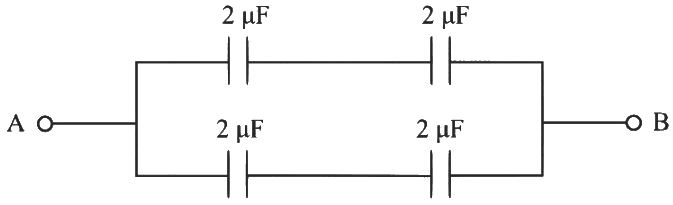
CAB = 1 + 1
= 2 μF
Q3: If the plates of a parallel plate capacitor connected to a battery are moved close to each other, then
A. the charge stored in it, increases.
B. the energy stored in it, decreases.
C. its capacitance increases.
D. the ratio of charge to its potential remains the same.
E. the product of charge and voltage increases.
Choose the most appropriate answer from the options given below:
(a) A, B and E only
(b) A, C and E only
(c) B, D and E only
(d) A, B and C only [2024]
Ans: (b)
Given V′ = V = Constant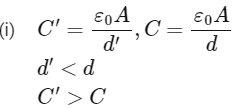
Hence, final capacitance greater than initial capacitance,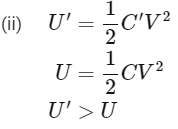
Hence final energy is greater than initial energy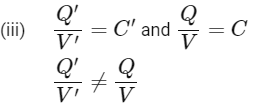
(iv) Product of charge and voltage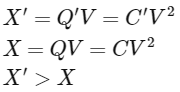
2023
Q1: An electric dipole is placed at an angle of 30° with an electric field of intensity 2 x 105NC-1 It experiences a torque equal to 4 N m. Calculate the magnitude of charge on the dipole, if the dipole length is 2 cm.(a) 6 mC
(b) 4 mC
(c) 2 mC
(d) 8 mC
Ans: (c)
The torque τ experienced by an electric dipole in an electric field is given by the formula:
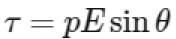
where p is the electric dipole moment, E is the electric field intensity, and θ is the angle between the dipole and the electric field. The electric dipole moment p can be expressed as:
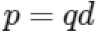
where q is the charge on the dipole, and d is the dipole length.
We are given the following values:
Torque τ = 4 N·m
Electric field intensity E = 2 x 105 NC-1 Angle, G = 30°
Dipole length, d = 2 cm = 0.02 m
We need to find the charge q on the dipole. Let's first solve for the electric dipole moment p:
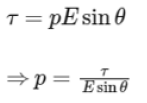
Substituting the given values:
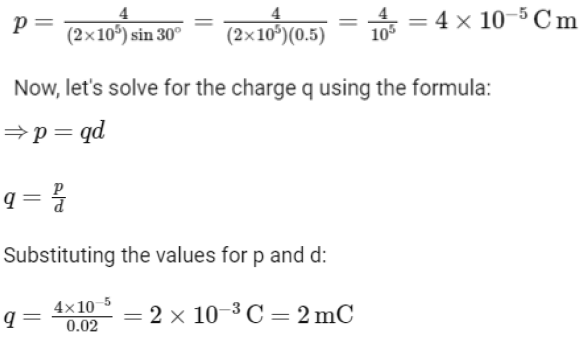
So, the magnitude of the charge on the dipole is 2 mC.
Q2: The equivalent capacitance of the system shown in the following circuit is: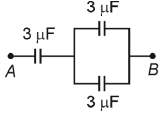
(a) 2 μF
(b) 3 μF
(c) 6 μF
(d) 9 μF
Ans: (a)
For parallel grouping
C1 = 3 + 3 = 6 μF
For series grouping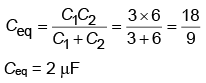
Q3: According to Gauss's law of electrostatics, electric flux through a closed surface depends on:
(a) the area of the surface
(b) the quantity of charges enclosed by the surface
(c) the shape of the surface
(d) the volume enclosed by the surface
Ans: (b)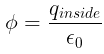 only depends on the charge enclosed by the surface.
only depends on the charge enclosed by the surface.
Q4: A charge Q /μC is placed at the center of a cube. The flux coming out from any one of its faces will be (in SI unit):
(a) 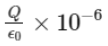
(b) 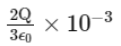
(c) 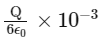
(d) 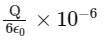
Ans: (d)
According to Gauss's law, the total electric flux Φtotal through a closed surface (in this case, the cube) is given by:
Total flux from cube =q/ϵ0
Since the charge Q is at the center of the cube, it is symmetrically enclosed, and the flux will be equally distributed across the six faces of the cube.
Thus, the flux through one face of the cube, Φface, is: 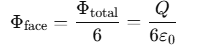
Since Q is given in microcoulombs (μC), we need to include the 10−6 factor: 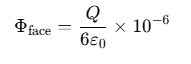
Q5: If a conducting sphere of radius R is charged. Then the electric field at a distance r(r > R) from the center of the sphere would be, (V = potential on the surface of the sphere)
(a) 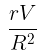
(b) 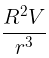
(c) 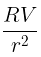
(d) V/r
Ans: (c)
For a charged conducting sphere, the electric field outside the sphere behaves like that of a point charge. The electric potential V on the surface of the sphere at r=R is given by: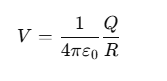
where Q is the total charge on the sphere.
At a distance r from the center of the sphere (where r>R), the electric potential Vr is: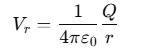
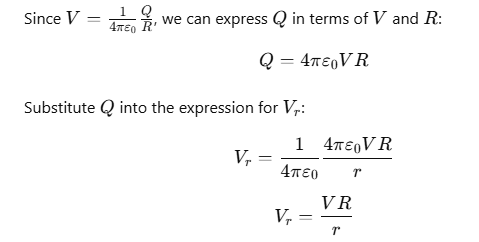
The electric field E is the negative gradient of the electric potential: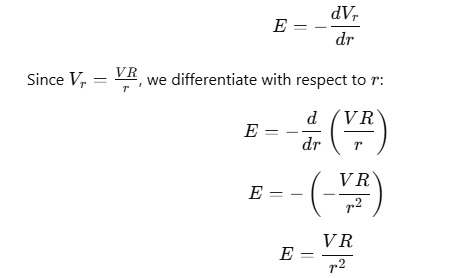
Q6: If 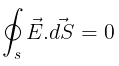 over a surface, then
over a surface, then
(a) the magnitude of the electric field on the surface is constant.
(b) all the charges must necessarily be inside the surface.
(c) the electric field inside the surface is necessarily uniform.
(d) the number of flux lines entering the surface must be equal to the number of flux lines leaving it,
Ans: (d)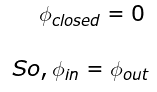

The number of field lines entering is equal to the number of field lines leaving.
Q7: An electric dipole is placed as shown in the figure.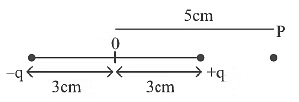 The electric potential (in 102 V) at point P due to the dipole is (ϵo - permittivity of free space and
The electric potential (in 102 V) at point P due to the dipole is (ϵo - permittivity of free space and 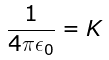
(a) (5/8) qK
(b) (8/5) qK
(c) (8/3) qK
(d) (3/8) qK
Ans: (d)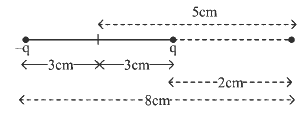
2022
Q1: Six charges +q, −q, +q, −q, +q, and −q are fixed at the corners of a hexagon of side d as shown in the figure. The work done in bringing a charge q0 to the centre of the hexagon from infinity is

(a) 
(b) Zero
(c) 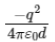
(d) 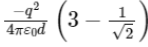
Ans: (b)
Since the charges are symmetrically arranged around the center of the hexagon, the net electric field at the center due to the six charges will be zero. This is because each positive charge is balanced by an opposite negative charge. However, we are concerned with the electric potential, not the electric field.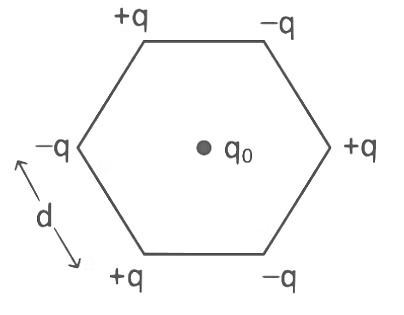
The electric potential at the center of the hexagon due to a point charge q located at a distance d is given by: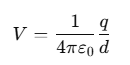
Since potential is a scalar quantity, we can add up the potentials due to each charge directly.
Potential due to each +q charge:

Potential due to each −q charge:
 Since there are three +q charges and three −q charges, the total potential at the center Vtotal is:
Since there are three +q charges and three −q charges, the total potential at the center Vtotal is: Thus, the net potential at the center of the hexagon is zero.
Thus, the net potential at the center of the hexagon is zero.
The work done W in bringing a charge q0 from infinity (where the potential is zero) to a point where the potential is Vtotal is given by:
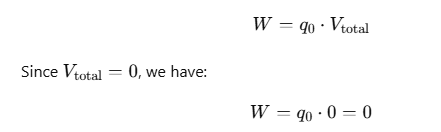
Q2: Two-point charges −q and +q is placed at a distance of L, as shown in the figure.
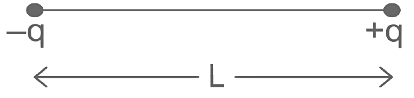
The magnitude of electric field intensity at a distance R(R >> L) varies as:
(a) 1/R2
(b) 1/R3
(c) 1/R4
(d) 1/R6
Ans: (b)
When two equal and opposite charges +q and −q are placed at a small separation L, they form an electric dipole with dipole moment: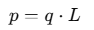
For an electric dipole, the electric field E at a point far away (where R≫L) from the dipole varies as: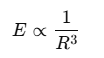
This result comes from the fact that at large distances, the field of a dipole decreases faster than that of a single point charge (which would vary as 1/R2). The dipole field specifically decreases as 1/R3.
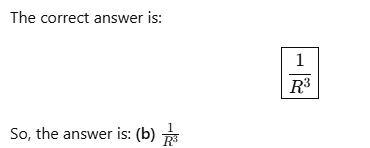
Q3: A capacitor of capacitance C = 900 pF is charged fully by 100 V battery B as shown in Figure (a). Then it is disconnected from the battery and connected to another uncharged capacitor of capacitance C = 900 pF as shown in Figure (b). The electrostatic energy stored by the system (b) is 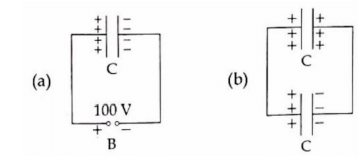
(a) 3.25 × 10–6 J
(b) 2.25 × 10–6 J
(c) 1.5 × 10–6 J
(d) 4.5 × 10–6 J
Ans: (b)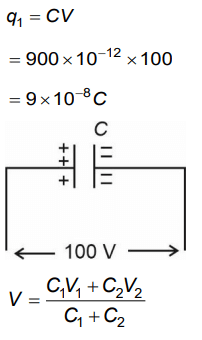
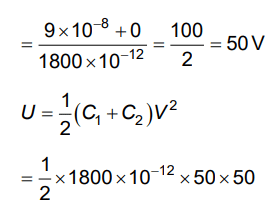
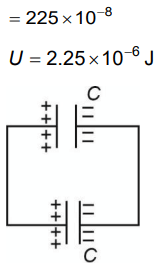
Q4: Two hollow conducting spheres of radii R1 and R2 (R1 >> R2) have equal charges. The potential would be
(a) More on the smaller sphere
(b) Equal in both the spheres
(c) Dependent on the material property of the sphere
(d) More on the bigger sphere
Ans: (a)
The potential of conducting hollow sphere = KQ/R
Now, Q = same
Q5: The angle between the electric lines of force and the equipotential surface is
(a) 45°
(b) 90°
(c) 180°
(d) 0°
Ans: (b)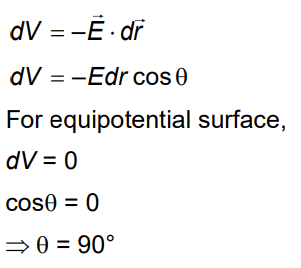
2021
Q1: A parallel plate capacitor has a uniform electric field E in the space between the plates. If the distance between the plates is d and the area of each plate is A , the energy stored in the capacitor is (ε0 = permittivity of free space).
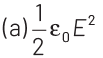
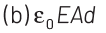
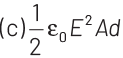
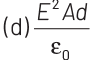
Ans: (c)

Q2: A parallel plate condenser has a uniform electric field E(V/m) in the space between the plates. If the distance between the plates is d(m) and the area of each plate is A(m2), the energy (joule) stored in the condenser is
(a) 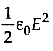
(b) 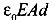
(c) 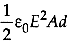
(d) 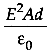
Ans: (c)
The capacitance of a parallel plate capacitor is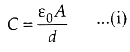
Potential difference between the plates is V = Ed ........ (ii)
The energy stored in the capacitor is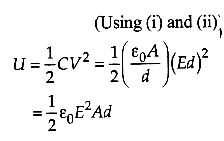
Q3: The equivalent capacitance of the combination shown in the figure is: 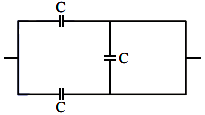 (a) C/2
(a) C/2
(b) 3C/2
(c) 3C
(d) 2C
Ans: (d)
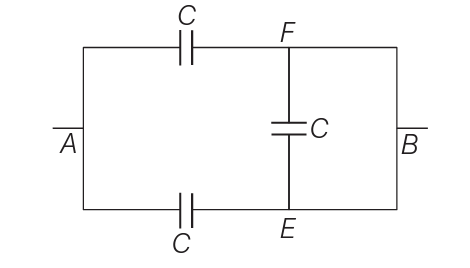
The voltage at node A matches the voltage at node B. Likewise, the voltage at node F is identical to the voltage at node E. Consequently, there is no voltage drop across the EF segment, leading to the absence of current (and therefore, no charge movement) within the circuit. Therefore, EF acts as if it were an open circuit. So the capacitor between the arms E and F gets short.
⇒ Ceq = C1 + C2
= C + C
= 2C
Q4: Two charged spherical conductors of radius R1 and R2 are connected by a wire. Then the ratio of surface charge densities of the spheres (σ1/σ2) is :
(a) 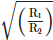
(b) 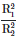
(c) 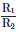
(d) 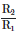
Ans: (d)
The surface charge density σ on a spherical conductor is given by: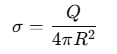
where Q is the total charge on the sphere, and R is the radius of the sphere.
Let the surface charge densities of the spheres with radii R1 and R2 be σ1 and σ2, respectively.
When the spheres are connected by a wire, they must have the same electric potential V.
The potential V on the surface of a spherical conductor with radius R and charge Q is given by: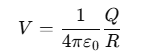
Since both spheres have the same potential: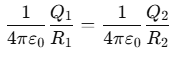
This simplifies to:
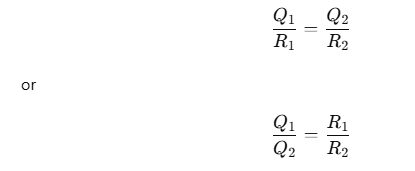
The surface charge density σ is related to Q by: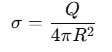

Q5: Twenty-seven drops of the same size are charged at 220 V each. They combine to form a bigger drop. Calculate the potential of the bigger drop.
(a) 1520 V
(b) 1980 V
(c) 660 V
(d) 1320 V
Ans: (b)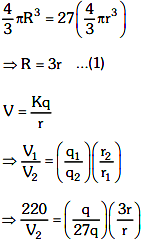
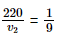 ⇒ V2 = 220 × 9
⇒ V2 = 220 × 9
= 1980 Volt
2020
Q1: The variation of electrostatic potential with radial distance r from the centre of a positively charged metallic thin shell of radius R is given by the graph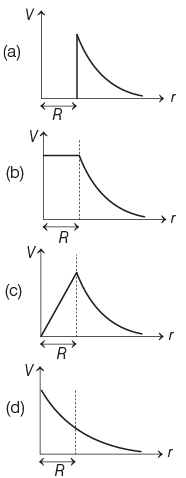
Ans: (b)
Since, electric potential remains constant inside the metallic spherical shell and same as the surface of spherical shell.
Outside the spherical shell, V ∝ 1/r
Hence, variation of potential (V ) with distance r is given as
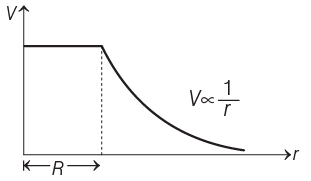
Q2: A short electric dipole has a dipole moment of 16 × 10−9 C-m. The electric potential due to the dipole at a point at a distance of 0.6 m from the centre of the dipole, situated on a line making an angle of 60° with the dipole axis is 
(a) 200 V
(b) 400 V
(c) zero
(d) 50 V
Ans: (a)
Given, electric dipole moment, p = 16 × 10−9 C-m
Distance, r = 0.6 m
Angle, θ = 60° ⇒ cos60° = 1/ 2
Electric potential at a point which is at a distance r at some angle θ from electric dipole is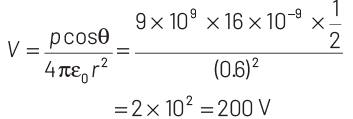
Hence, correct option is (a).
Q3: In a certain region of space with a volume of 0.2 m3, the electric potential is found to be 5 V throughout. The magnitude of the electric field in this region is:
(a) 1 N/C
(b) 5 N/C
(c) Zero
(d) 0.5 N/C
Ans: (c)
given V = const. (5 volts)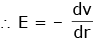
E = 0
Q4: The capacitance of a parallel plate capacitor with air as the medium is 6 μF. With the introduction of a dielectric medium, the capacitance becomes 30 μF. The permittivity of the medium is :
(ε0 = 8.85×10-12 C2 N-1 m-2)
(a) 0.44×10-10 C2 N-1 m-2
(b) 5.00 C2 N-1 m-2
(c) 0.44×10-13 C2 N-1 m-2
(d) 1.77×10-12 C2 N-1 m-2
Ans: (a)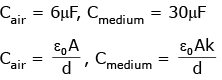
Cmed = KCair
30μF = K6μF
K = 5
∴ ε = ε0k = 8.85 × 10-12 × 5
ε = 44.25 × 10-12
ε = 0.4425 × 10-10
ε = 0.44 × 10-10 C2N-1m-2
Q5: A 40 μF capacitor is connected to a 200 V, 50 Hz AC supply. The RMS value of the current in the circuit is, nearly:
(a) 2.5 A
(b) 25.1 A
(c) 1.7 A
(d) 2.05 A
Ans: (a)
The capacitive reactance XC in an AC circuit is given by: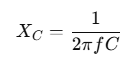
Substitute the values: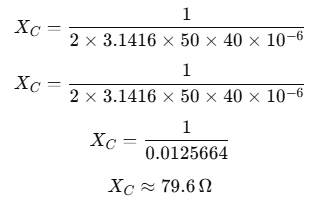
The RMS current IRMS in an AC circuit with a capacitor is given by: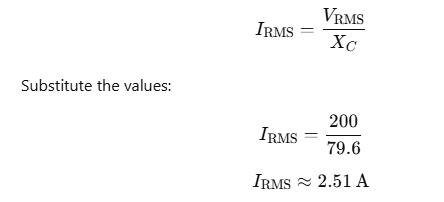
The RMS value of the current in the circuit is approximately: 2.5A
2019
Q1: Two metal spheres, one of radius R and the other of radius 2R respectively have the same surface charge density σ. They are brought in contact and separated. What will be the new surface charge densities on them?
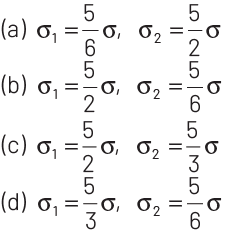
Ans: (d)
The surface charge density of a closed surface area having charge Q is given by
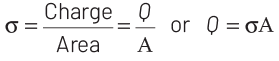
Thus, the charges on sphere P and Q having same charge density as shown in the figure below is given by
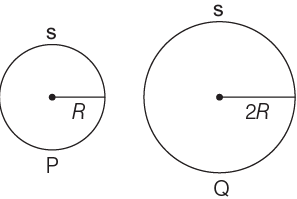
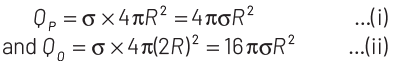
when they are brought in contact with each other, the total charge will be
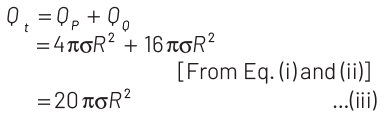
In connection of two charged conducting bodies, the potential will become same on both, i.e.
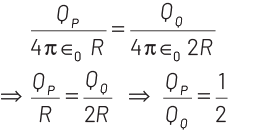
So, the charges on the sphere P and Q after separation will be distributed as
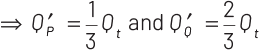
After separation, the new surface charge densities on P and Q will be
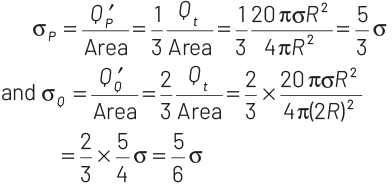
Q2: Two identical capacitors C1 and C2 of equal capacitance are connected as shown in the circuit.
Terminals a and b of the key k are connected to charge capacitor C1 using battery of emf V volt. Now, disconnecting a and b the terminals b and c are connected.
Due to this, what will be the percentage loss of energy?
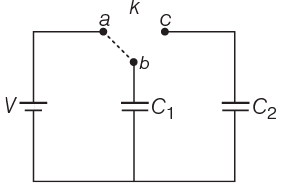
(a) 75%
(b) 0%
(c) 50%
(d) 25%
Ans: (c)
When C1 is connected to voltage source, it is charged to a potential V and this will be stored as a potential energy in the capacitor given by
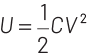

When key is disconnected from battery and b and c are connected, the charge will be transformed from the capacitor C1 to capacitor C2 , then

The loss of energy due to redistribution of charge is given by
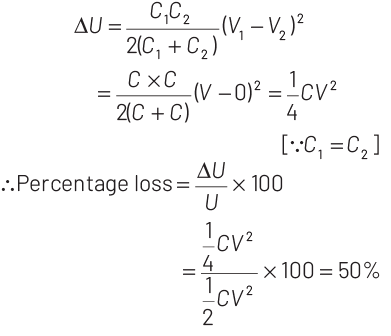
2018
Q1: The electrostatic force between the metal plates of an isolated parallel plate capacitor C having a charge Q and area A, is:
(a) independent of the distance between the plates.
(b) linearly proportional to the distance between the plates
(c) proportional to the square root of the distance between the plates.
(d) inversely proportional to the distance between the plates.
Ans: (a)
Solution:
F = QE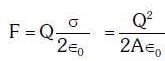
∴ The electrostatic force is independent of the distance between plates.
2017
Q1: A capacitor is charged by a battery. The battery is removed and another identical uncharged capacitor is connected in parallel. The total electrostatic energy of the resulting system:
(a) Decreases by a factor of 2
(b) Remains the same
(c) Increases by a factor of 2
(d) Increases by a factor of 4
Ans: (a)
Solution: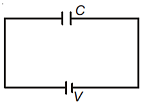
Charge on capacitor
q = CV
when it is connected to another uncharged capacitor.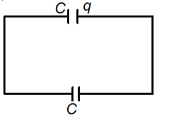
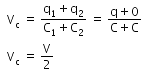
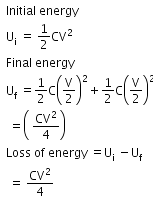
Q2: The diagrams below show regions of equipotentials: 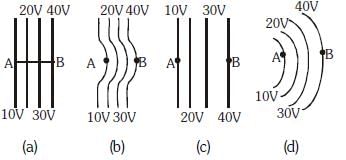 A positive charge is moved from A to B in each diagram.
A positive charge is moved from A to B in each diagram.
(a) Maximum work is required to move q in Figure (c)
(b) Minimum work is required to move q in Figure (a)
(c) Maximum work is required to move q in Figure (b)
(d) In all four cases the work done is the same
Ans: (d)
Solution:
W = qΔV
as ΔV is the same in all conditions, work will be the same.
2016
Q1: A parallel-plate capacitor of area A, plate separation d and capacitance C is filled with four dielectric materials having dielectric constants k1, k2, k3 and k4 as shown in the figure below. If a single dielectric material is to be used to have the same capacitance C in this capacitor, then its dielectric constant k is given by
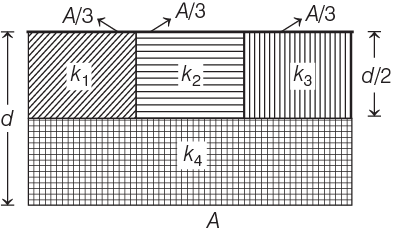
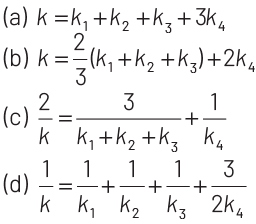
Ans: (c)
Step 1: Understanding the Arrangement
- The top three sections (with k1, k3) are connected in parallel because they share the same potential difference (as they are in the same horizontal plane).
- The bottom section (with k4) is in series with the combined capacitance of the top three sections.
Step 2: Capacitance of Each Section
The capacitance C of a parallel-plate capacitor with dielectric constant k, area A, and separation d is given by: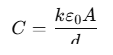

Step 3: Equivalent Capacitance
The top and bottom sections are in series, so the total capacitance C is given by:
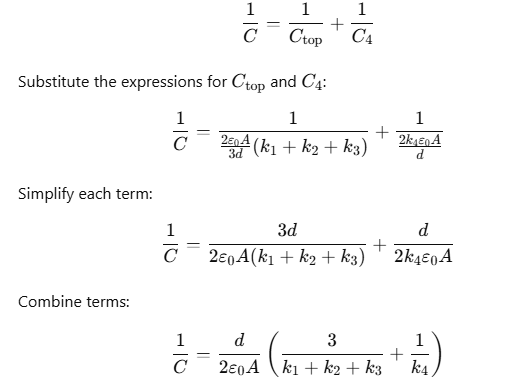
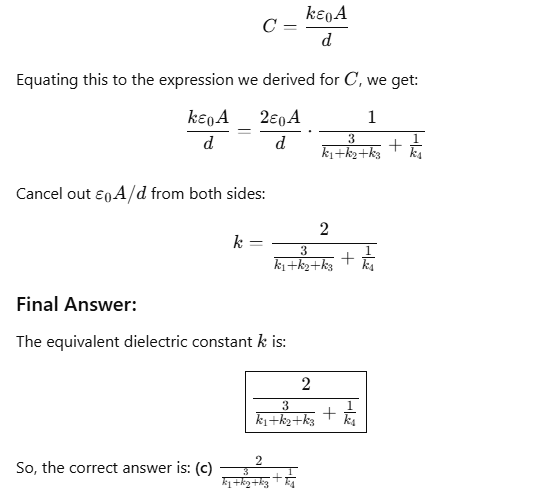
Step 4: Equivalent Dielectric Constant
We want the equivalent capacitance C to be the same as if the entire capacitor had a single dielectric constant k, so:
Q2: A capacitor of 2µF is charged as shown in the diagram. When the switch S is turned to position 2, the percentage of its stored energy dissipated is : 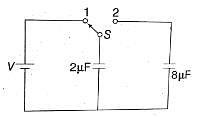
(a) 80%
(b) 0%
(c) 20%
(d) 75%
Ans: (a)
Solution:
Consider the figure given above.
When switch S is connected to point 1, the initial energy stored in the capacitor is given as,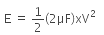
When the switch S is connected to point 2, energy dissipated on connection across 8μF will be,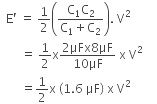 Therefore, the percentage loss of energy
Therefore, the percentage loss of energy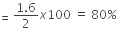
2015
Q1: If potential (in volts) in a region is expressed as V (x, y, z) = 6xy − y + 2yz, the electric field (in N/C) at point (1, 1, 0) is [CBSE AIPMT 2015] (a) 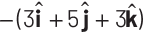
(b) 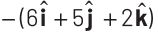
(c) 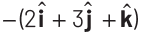
(d) 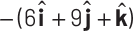
Ans: (b)
Given, potential in a region,
V = 6xy − y + 2yz.
Electric field in a region,
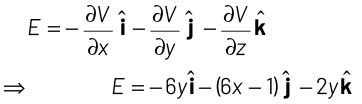
At, (1, 1, 0), electric field can be expressed,
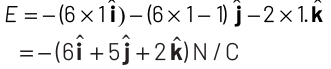
Q2: A parallel plate air capacitor of capacitance C is connected to a cell of emf V and then disconnected from it. A dielectric slab of dielectric constant K, which can just fill the air gap of the capacitor, is now inserted in it. Which of the following is incorrect?
(a) The charge on the capacitor is not conserved.
(b) The potential difference between the plates decreases K times
(c) The energy stored in the capacitor decreases K times
(d) the change in energy stored is 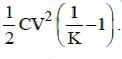 Ans: (a)
Ans: (a)
Solution:
A parallel plate air capacitor of capacitance C is connected to a cell of emf V and then disconnected from it.
The charge on the capacitor is given by
Q = CV
The energy stored in the capacitor is
E = 1/2 CV2
When a dielectric slab of dielectric constant K is inserted in it, the charge Q is conserved.
The capacitance becomes K times the original capacitance. (C' = KC)
The voltage becomes 1/K time the original voltage
V' = V/K
The change in energy stored is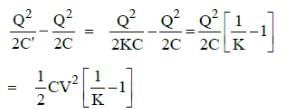
2014
Q1: In a region, the potential is represented by V(x, y, z) = 6x − 8xy − 8y + 6yz, where V is in volts and x, y, and z are in meters. The electric force experienced by a charge of 2 coulombs situated at point (1,1,1) is:
(a) 24N
(b)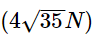
(c)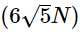
(d) 30N
Ans: (b)
Solution: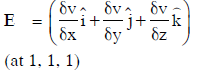
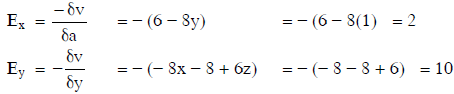
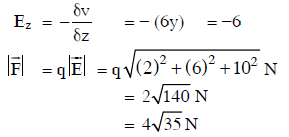 Q2: A conducting sphere of radius R is given a charge Q. The electric potential and the electric field at the center of the sphere respectively are :
Q2: A conducting sphere of radius R is given a charge Q. The electric potential and the electric field at the center of the sphere respectively are :
(a)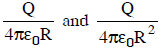
(b) Both are zero
(c)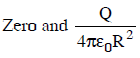
(d)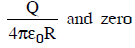
Ans: (d)
Solution: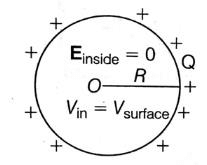
The electric field inside, Einside = 0
Potential, Vinside = Vsurface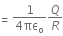
|
97 videos|336 docs|104 tests
|
FAQs on NEET Previous Year Questions (2014-2024): Electrostatics Potential & Capacitance - Physics Class 12
| 1. What is the formula for calculating the electric potential due to a point charge? |  |
| 2. How is the electric potential energy related to the electric potential in a system of charges? |  |
| 3. What is the difference between electric potential and electric potential energy? |  |
| 4. How does the capacitance of a capacitor affect its ability to store electric charge? |  |
| 5. How can the capacitance of a parallel plate capacitor be increased? |  |

|
Explore Courses for NEET exam
|

|
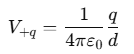
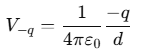 Since there are three +q charges and three −q charges, the total potential at the center Vtotal is:
Since there are three +q charges and three −q charges, the total potential at the center Vtotal is: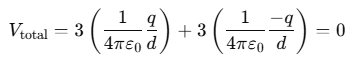 Thus, the net potential at the center of the hexagon is zero.
Thus, the net potential at the center of the hexagon is zero.

















