NEET Previous Year Questions (2014-2024): Electromagnetic Induction | Physics Class 12 PDF Download
2024
Q1: In the below diagram, a strong bar magnet is moving towards solenoid-2 from solenoid-1. The direction of induced current in solenoid-1 and that in solenoid-2, respectively, are through the directions: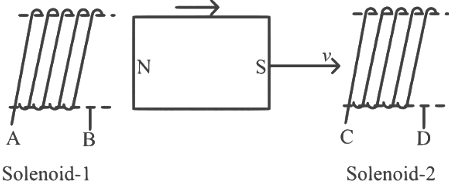 (a) AB and DC
(a) AB and DC
(b) BA and CD
(c) AB and CD
(d) BA and DC [2024]
Ans: (a)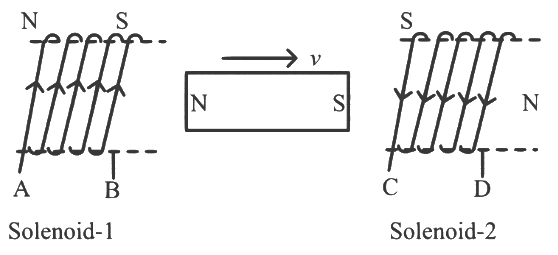 North of magnet is moving away from solenoid 1 so end B of solenoid 1 is South
North of magnet is moving away from solenoid 1 so end B of solenoid 1 is South
and as south of magnet is approaching solenoid 2 so end C of solenoid 2 is South.
2023
Q1: An ac source is connected in the given circuit. The value of 0 will be :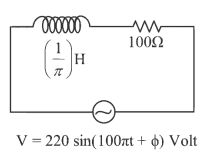 (a) 60o
(a) 60o
(b) 90o
(c) 30o
(d) 45o
Ans: (d)
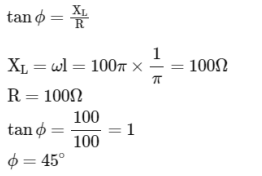
Q2: If Z1 and Z2 are the impedances of the given circuits (a) and (b) as shown in figures, then choose the correct option
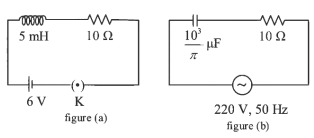
(a) Z1 < Z2
(b) Z1 + Z2 = 20 Ω
(c) Z1 = Z2
(d) Z1 >Z2
Ans: (a)
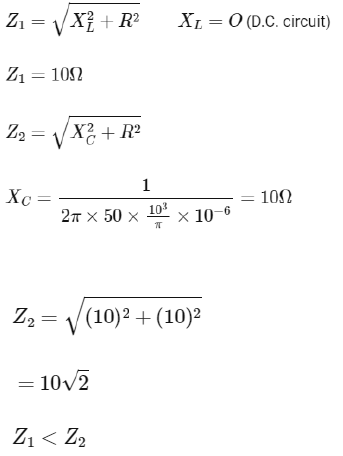
Q3: The maximum power is dissipated for an ac in a/an:
(a) resistive circuit
(b) LC circuit
(c) inductive circuit
(d) capacitive circuit
Ans: (a)
Power dissipated is maximum of purely resistive circuit.
Q4: An emf is generated by an ac generator having 100 turn coil, of loop area 1 m2. The coil rotates at a speed of one revolution per second and placed in a uniform magnetic field of 0.05 T perpendicular to the axis of rotation of the coil. The maximum value of emf is :-
(a) 3.14 V
(b) 31.4 V
(c) 62.8 V
(d) 6.28 V
Ans: (b)
Q5: For very high frequencies, the effective impedance of the circuit (shown in the figure) will be:-
 (a) 4 Ω
(a) 4 Ω
(b) 6 Ω
(c) 1 Ω
(d) 3 Ω
Ans: (d)
As frequency is very high
XC ≈ 0
XL → α
Effective circuit will be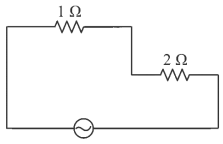
Effective impedance of circuit will be = 3Ω
Q6: In a series LCR circuit, the inductance L is 10 mH, capacitance C is 1 μF and resistance R is 100Ω. The frequency at which resonance occurs is
(a) 15.9 kHz
(b) 1.59 rad/s
(c) 1.59 kHz
(d) 15.9 rad/s
Ans: (c)
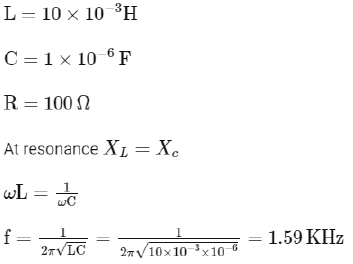
Q7: The net magnetic flux through any closed surface is :
(a) Positive
(b) Infinity
(c) Negative
(d) Zero
Ans: (d)
Magnetic field exist in Closed Loops (Monopoles do not exist)
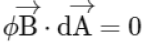
(Gauss law for magnetism)
Q8: A 12 V,60 W lamp is connected to the secondary of a step down transformer, whose primary is connected to ac mains of 220 V. Assuming the transformer to be ideal, what is the current in the primary winding ?
(a) 2.7 A
(b) 3.7 A
(c) 0.37 A
(d) 0.27 A
Ans: (d)
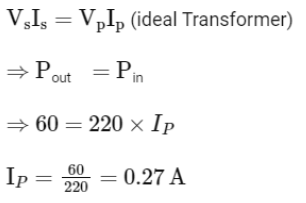
Q9: An ac source is connected to a capacitor C. Due to decrease in its operating frequency
(a) displacement current increases.
(b) displacement current decreases.
(c) capacitive reactance remains constant.
(d) capacitive reactance decreases.
Ans: (b)
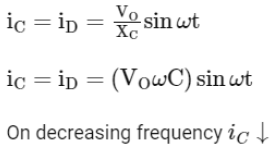
Q10: The magnetic energy stored in an inductor of inductance 4 μH carrying a current of 2 A is
(a) 4 μJ
(b) 4 mJ
(c) 8 mJ
(d) 8 μJ
Ans: (d)
Solution: Magnetic energy stored in an inductor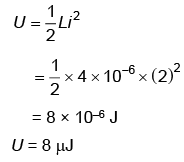
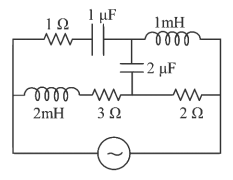
Q11: The net impedance of circuit (as shown in figure) will be:
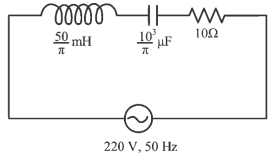
(a) 15 Ω
(b) 5√5 Ω
(c) 25 Ω
(d) 10√2 Ω
Ans: (b)
2022
Q1: A closely packed coil having 1000 turns has an average radius of 62.8 cm. If current carried by the wire of the coil is 1 A, the value of magnetic field produced at the centre of the coil will be (permeability of free space =4π×10−7 H/m) nearly
(a) 10-3T
(b) 10-1T
(c) 10-2T
(d) 102T
Ans: (a)
Magnetic field at the centre of coil
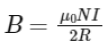
On substituting the given values
Q2: Given below are two statements
Statement I : In an a.c circuit, the current through a capacitor leads the voltage across it.
Statement II : In a.c circuit containing pure capacitance only, the phase difference between the current and voltage is π.
In the light of the above statements, choose the most appropriate answer from the options given below:
(a) Statement I is incorrect but Statement II is correct
(b) Both Statement I and Statement II are correct
(c) Both Statement I and Statement II are incorrect
(d) Statement I is correct but Statement II is incorrect
Ans: (d)
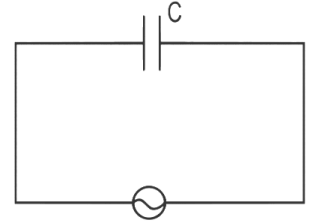
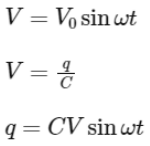
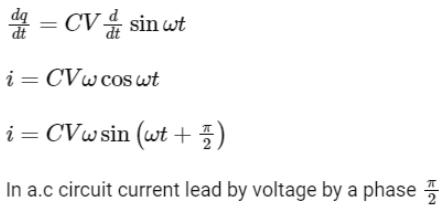
Thus statement I is correct while II is incorrect.
Q3: An inductor of inductance 2 mH is connected to a 220 V, 50 Hz ac source. Let the inductive reactance in the circuit is X1. If a 220 V dc source replace the ac source in the circuit, then the inductive reactance in the circuit is X2, X1 and X2 respectively are :
(a) 0.628 Ω, infinity
(b) 6.28 Ω, zero
(c) 6.28 Ω, infinity
(d) 0.628 Ω, zero
Ans: (d)
We know, for A.C. Source
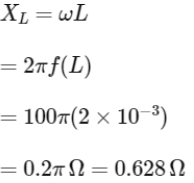
For D.C. Source
The inductor behaves as a closed circuit offering no resistance at all (at steady state) as w = 0 (For D.C.)
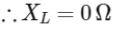
Q4: A standard filament lamp consumes 100 W when connected to 200 V ac mains supply. The peak current through the bulb will be :
(a) 2 A
(b) 0.707 A
(c) 1 A
(d) 1.414 A
Ans: (b)
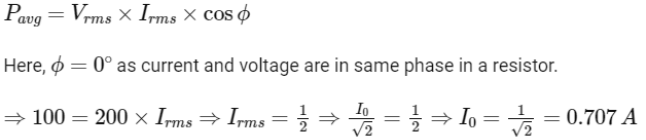
Q5: The magnetic flux linked to a circular coil of radius R is.
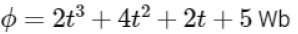
The magnitude of induced emf in the coil at t = 5 s is
(a) 192 V
(b) 108 V
(c)197 V
(d) 150 V
Ans: (a)
Given magnetic flux is
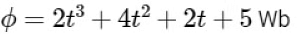
Induced emf is given by
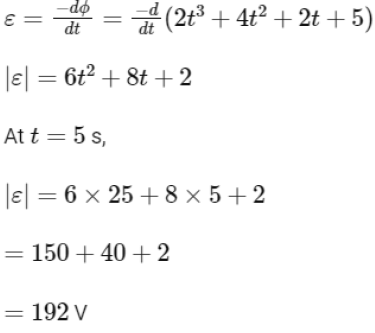
Q6: The peak voltage of the ac source is equal to
(a) The value of voltage supplied to the circuit
(b) The rms value of the ac source
(c) √2 times the rms value of the ac source
(d) 1/√2 times the rms value of the ac source
Ans: (c)
We know,
RMS value of A.C. 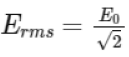
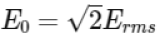
Q7: The energy that will be ideally radiated by a 100 kW transmitter in 1 hour is
(a) 36 x 107 J
(b) 36 x 104 J
(c) 36 x 105 J
(d) 1 x 105 J
Ans: (a)
Energy = Power x Time
E = 100 x 103 x 3600
36 x 107 J
Q8: A series LCR circuit with inductance 10 H, capacitance 10 μF, resistance 50 Ω is connected to an ac source of voltage, V = 200sin(100t) volt. If the resonant frequency of the LCR circuit is v0 and the frequency of the ac source is v, then
(a) 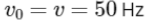
(b) 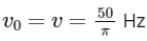
(c) 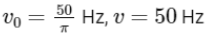
(d) 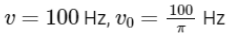
Ans: (b)
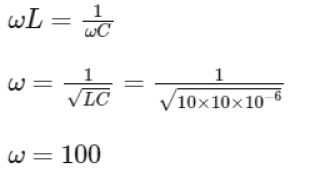
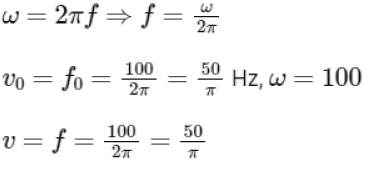
Q9: A big circular coil of 1000 turns and an average radius of 10 m is rotating about its horizontal diameter at 2 rad s–1 . If the vertical component of the earth’s magnetic field at that place is 2 × 10–5 T and the electrical resistance of the coil is 12.56 ohm, then the maximum induced current in the coil will be
(a) 1.5 A
(b) 1 A
(c) 2 A
(d) 0.25 A
Ans: (b)
Solution: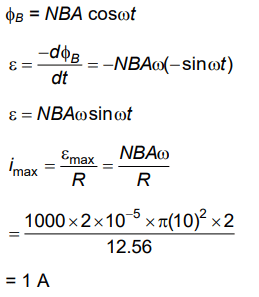
Q10: A square loop of side 1 m and resistance 1Ω is placed in a magnetic field of 0.5 T. If the plane of the loop is perpendicular to the direction of the magnetic field, the magnetic flux through the loop is
(a) 0.5 weber
(b) 1 Weber
(c) Zero Weber
(d) 2 Weber
Ans: (a)
Solution: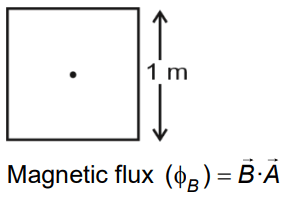
2021
Q1: Two conducting circular loops of radii R1 and R2 are placed in the same plane with their centres coinciding. If R1 >> R2, the mutual inductance M between them will be directly proportional to
(a) R1/R2
(b) R2/R1
(c) R12/R2
(d) R22/R1
Ans: (d)
Solution:
The magnetic field at the centre of the primary coil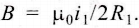 Considering it to be uniform, magnetic flux passing through the secondary coil is
Considering it to be uniform, magnetic flux passing through the secondary coil is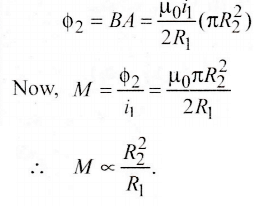
2020
Q1: The magnetic flux linked with a coil (in Wb) is given by the equation φ = 5t2 + 3t + 16 The magnitude of induced emf in the coil at the fourth second will be
(a) 33 V
(b) 43 V
(c) 108 V
(d) 10 V
Ans: (d)
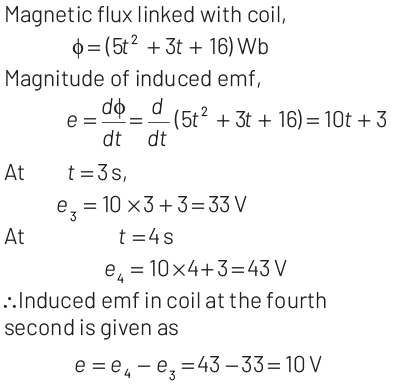
Q2: A wheel with 20 metallic spokes each 1 m long is rotated with a speed of 120 rpm in a plane perpendicular to a magnetic field of 0.4 G. The induced emf between the axle and rim of the wheel will be (1 G = 10−4 T)
(a) 2.51 × 10−4 V
(b) 2.51 × 10−5 V
(c) 4.0 × 10−5 V
(d) 2.51 V
Ans: (a)
Given, magnetic field,
B = 0.4 G = 0.4 × 10 − 4T
l = 1m
Frequency, f = 12 rpm = 120 / 60 rps = 2 Hz
Induced emf between the axle and rim of the wheel is given as
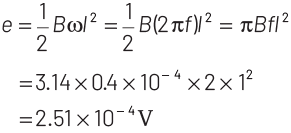
Q3: A light bulb and an inductor coil are connected to AC ac source through a key as shown in the figure below. The key is closed and after sometime an iron rod is inserted into the interior of the inductor. The glow of the light bulb
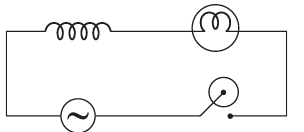 (a) decreases
(a) decreases
(b) remains unchanged
(c) will fluctuate
(d) increases
Ans: (a)
When an iron rod is inserted into the interior of the inductor, then inductance (L) of the coil increases.
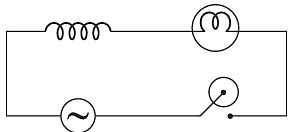
Hence, inductive reactance (XL = ωL)also increases.
∴ Current in the circuit is given as
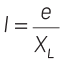
Hence, when XL increases, then current I decreases. Therefore, glow of the light bulb will decrease.
2019
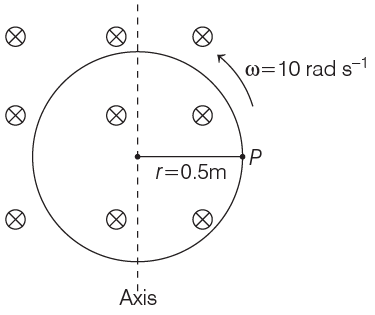
Q1: A cycle wheel of radius 0.5 m is rotated with constant angular velocity of 10 rad/s in a region of magnetic field of 0.1 T which is perpendicular to the plane of the wheel. The EMF generated between its centre and the rim is
(a) 0.25 V
(b) 0.125 V
(c) 0.5 V
(d) zero
Ans: (b)
When a conducting disc or wheel of radius r rotates with constant angular velocity of ω about its axis in a uniform magnetic field perpendicular to its plane and parallel to its axis of rotation, then,
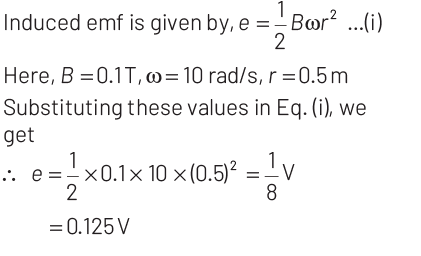
Q2: A coil of 800 turns effective area 0.05 m 2 is kept perpendicular to a magnetic field 5 × 10−5 T. When the plane of the coil is rotated by 90º around any of its co-planar axis in 0.1 s, the emf induced in the coil will be
(a) 0.2 V
(b) 2 ×10−3 V
(c) 0.02 V
(d) 2 V
Ans: (c)
Given,
area of coil, A = 0.05 m2
magnetic field, B = 5 × 10 −5 T and
number of turns, N = 800 .
The magnetic flux linked with the coil is
φ = N (B ⋅ A) = N BA cosθ … (i)
where, θ is the angle between B and A.
The emf induced when coil is rotated from θ1 = 0° to θ2 = 90° is
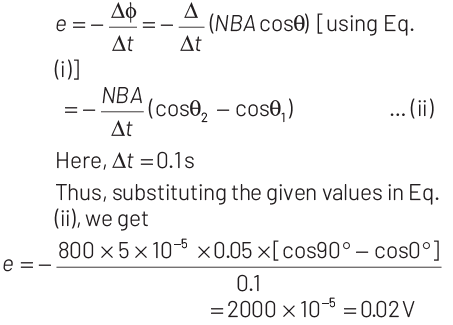
Q3: An 800 turn coil of effective area 0.05 m2 is kept perpendicular to a magnetic field 5 × 10–5 T. When the plane of the coil is rotated by 90° around any of its coplanar axes in 0.1 s, the emf-induced in the coil will be: (2019)
(a) 2 V
(b) 0.2 V
(c) 2 x 10-3 V
(d) 0.02 V
Ans: (d)
Solution:
Magnetic field B = 5 × 10–5 T
Number of turns in coil N = 800
Area of coil A = 0.05 m2
Time taken to rotate Δt = 0.1 s
Initial angle θ1 = 0°
Final angle θ2 = 90°
Change in magnetic flux Δφ
= N[BAcos90° – BAcos0°]
= – NBA
= – 800 × 5 × 10–5 × 0.05
= – 2 × 10–3 Weber
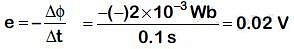
Q4: In which of the following devices, the eddy current effect is not used?
(a) Induction furnace
(b) Magnetic braking in train
(c) Electromagnet
(d) Electric heater
Ans: (d)
Solution:
A. Induction Furnace: Eddy currents are used in induction furnaces to heat metal for melting or heating purposes. The metal is placed inside a coil, and alternating current passes through the coil, inducing eddy currents in the metal, which heats it up due to its electrical resistance.
B. Magnetic Braking in Train: Eddy currents are used in magnetic braking systems in trains. When a train's metal wheels pass through a magnetic field, eddy currents are induced in the wheels, creating a force that opposes the motion of the train, slowing it down.
C. Electromagnet: Eddy currents can have an undesirable effect on electromagnets because they can cause energy loss and heating. However, in devices like transformers and electric motors, eddy currents can be minimized by using laminated cores or by using materials with high electrical resistivity.
D. Electric Heater: Electric heaters typically do not use the eddy current effect. Instead, they use the resistance of a material to convert electrical energy into heat. The electric current passes through a resistive element, such as a wire or a coil, which heats up and transfers heat to the surrounding area.
2018
Q1: The magnetic potential energy stored in a certain inductor is 25 mJ, when the current in the inductor is 60 mA.
This inductor is of inductance
(a) 1.389 H
(b) 138.88 H
(c) 0.138 H
(d) 13.89 H
Ans: (d)
Given, magnetic potential energy stored in an inductor,
U = 25 mJ = 25 × 10 −3 J
Current in an inductor, I0 = 60 mA = 60 × 10−3 A
As, the expression for energy stored in an inductor is given as
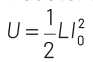
where, L is the inductance of the inductor.
Substituting the given values in above equation., we get
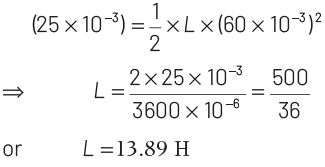
Q2: A metallic rod of mass per unit length 0.5 kg m–1 is lying horizontally on a smooth inclined plane which makes an angle of 30° with the horizontal. The rod is not allowed to slide down by flowing a current through it when a magnetic field of induction 0.25T is acting on it in the vertical direction. The current flowing in the rod to keep it stationary is
(a) 7.14 A
(b) 5.98 A
(c) 14.76 A
(d) 11.32 A
Ans: (d)
Solution:
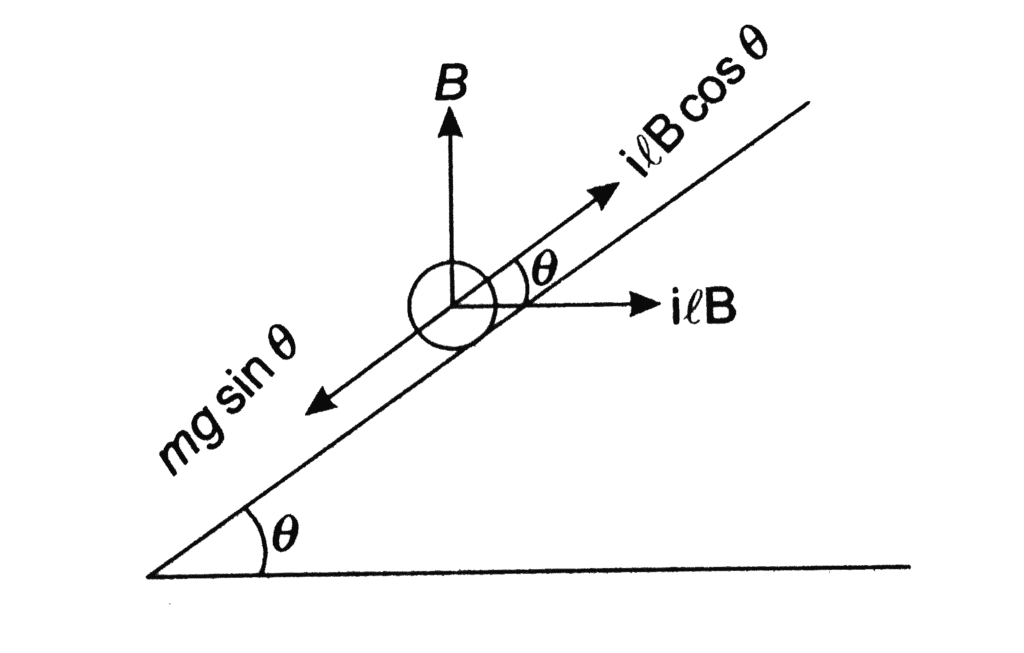
To keep the rod stationary on the inclined plane, the force due to the magnetic field acting upwards must balance the component of the gravitational force acting downwards along the inclined plane.
The gravitational force component acting down the incline is given by: Fgravity=mgsin(θ) where:
m is the mass per unit length of the rod,
g is the acceleration due to gravity, and
θ is the angle of inclination.
The magnetic force acting upwards is given by: Fmagnetic=IℓB cosθ where:
I is the current flowing through the rod,
ℓ is the length of the rod, and
B is the magnetic field induction.
For equilibrium, Fgravity=Fmagnetic: mg sinθ=IℓB cosθ
Given:
m=0.5 kg/m (mass per unit length),
θ=30∘,
B=0.25 T, and
g=9.81 m/s²,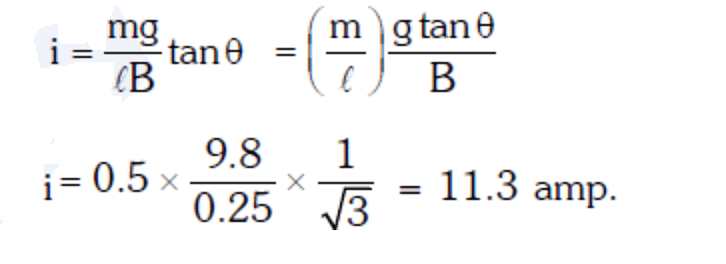 Q3: A thin diamagnetic rod is placed vertically between the poles of an electromagnet. When the current in the electro-magnet is switched on, then the diamagnetic rod is pushed up, out of the horizontal magnetic field. Hence the rod gains gravitational potential energy. The work required to do this comes from
Q3: A thin diamagnetic rod is placed vertically between the poles of an electromagnet. When the current in the electro-magnet is switched on, then the diamagnetic rod is pushed up, out of the horizontal magnetic field. Hence the rod gains gravitational potential energy. The work required to do this comes from
(a) the current source
(b) the magnetic field
(c) the lattice structure of the material of the rod
(d) the induced electric field due to the changing magnetic field
Ans: (a)
Solution:
When the current source is switched on, a magnetic field is set up between the poles on the electromagnet. Diamagnetic material, due to its tendency to move from a stronger to a weaker field, is thus repelled out
2017
Q1: A long solenoid of diameter 0.1 m has 2 × 104 turns per meter. At the centre of the solenoid, a coil of 100 turns and a radius of 0.01 m is placed with its axis coinciding with the solenoid axis. The current in the solenoid reduces at a constant rate to 0 A from 4 A in 0.05 s. If the resistance of the coil is 10π2Ω. The total charge flowing through the coil during this time is:(a) 16 μC
(b) 32 μC
(c) 16 π μC
(d) 32 π μC
Ans: (b)
Solution:
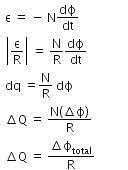
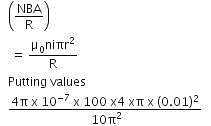
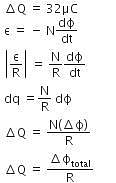

2016
Q1: A uniform magnetic field is restricted within a region of radius r. The magnetic field changes with time at a rate dB/dT. Loop 1 of radius R > r encloses the region r and loop 2 of radius R is outside the region of magnetic field as shown in the figure. Then, the emf generated is
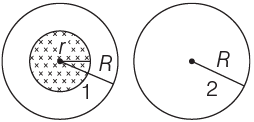

Ans: (c)
Induced emf in the region is given by
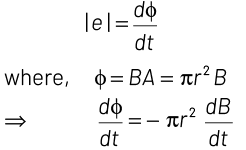
Rate of change of magnetic flux associated with loop 1
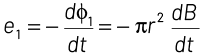
Similarly e2 = emf associated with loop 2

Q2: A long solenoid has 1000 turns. When a current of 4A flows through it, the magnetic flux linked with each turn of the solenoid is 4 x 10-3 Wb. The self-inductance of the solenoid is
(a) 1H
(b) 4H
(c) 3H
(d) 2H
Ans: (a)
Solution:
Given,
Number of turns in the solenoid, N = 1000
Current, I = 4 A
Magnetic flux, straight phi subscript straight B = 4 x 10-3 Wb
Self-inductance of the solenoid is given by,
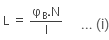
Putting the value of the equation in (i), we get
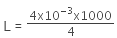
= 1H
2015
Q1: An electron moves on a straight line path XY as shown. The abcd is a coil adjacent in the path of electron. What will be the direction of current, if any induced in the coil?
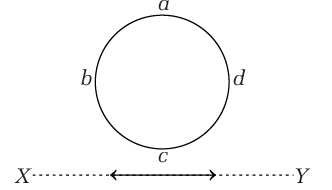
(a) abcd
(b) adcb
(c) The current will reverse its direction as the electron goes past the coil
(d) No current induced
Ans: (d)
First current develops in direction of abcd but when electron moves away then magnetic field inside loop decreases and current changes its direction.
Q2: A conducting square frame of side 'a‘ and a long straight wire carrying current I are located in the same plane as shown in the figure. The frame moves to the right with a constant velocity 'V‘. The emf induced in the frame will be proportional to :
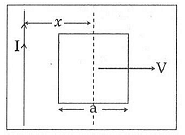
(a)
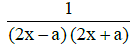
(b)
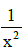
(c)
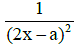
(d)
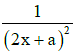
Ans: (a)
Solution:
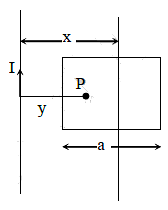
See figure alongside.
Let x be the distance of the centre of the frame from the long straight wire carrying current I.
Consider the point P at a distance y from the long straight wire carrying current I.
The strength of magnetic induction at point P is given by
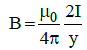
Integrating over y from y = (x - a/2) to y = (x + a/2)
We get
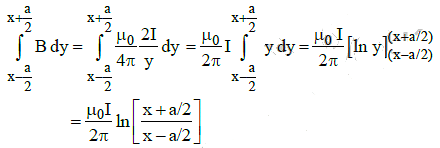
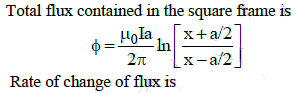
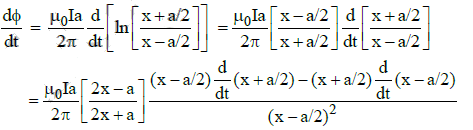
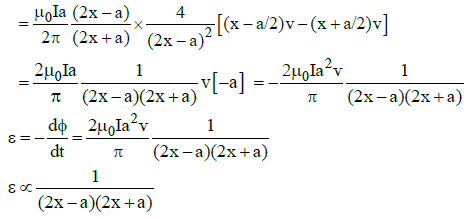
2014
Q1: A thin semicircular conducting ring (PQR) of radius ‘r’ is falling with its plane vertical in a horizontal magnetic field B, as shown in figure. The potential difference developed across the ring when its speed is v, is : 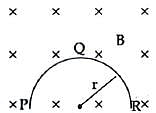
(a) πrBv and R is at higher potential
(b) 2rBv and R is at higher potential
(c) Zero
(d) Bvπr2/2 & P is at a higher potential
Ans: (b)
Solution:
Effective length = 2r
Potential developed = 2rBv
|
98 videos|334 docs|102 tests
|
FAQs on NEET Previous Year Questions (2014-2024): Electromagnetic Induction - Physics Class 12
| 1. What is Faraday's law of electromagnetic induction? |  |
| 2. How is Lenz's law related to electromagnetic induction? |  |
| 3. What is the difference between self-induction and mutual induction? |  |
| 4. How does the number of turns in a coil affect the induced emf in electromagnetic induction? |  |
| 5. Can electromagnetic induction be used to generate electricity? |  |




















