NEET Previous Year Questions (2014-2024): Mechanical Properties of Solids | Physics Class 11 PDF Download
2024
Q1: The maximum elongation of a steel wire of 1m length if the elastic limit of steel and its Young's modulus, respectively, are 8 × 108 Nm−2 and 2 × 1011 Nm−2, is: [2024]
(a) 4 mm
(b) 0.4 mm
(c) 40 mm
(d) 8 mm
Ans: (a)
First, we need to find the maximum force that can be applied to the steel wire within its elastic limit. This force can be calculated using the given area under stress and the stress limit provided by the elastic limit of steel.
Let's assume the area of cross-section of the wire is A. The force exerted can be given by: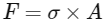
where:
σ
To calculate the elongation (ΔL) under this force, we use Hooke's Law, which relates force, elongation, cross-sectional area, original length, and Young's modulus as follows:
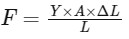
where:
Y = 2 x 1011 N / m2 (Young's modulus of steel),
L = 1 m (original length of the wire).
Substituting for F from the earlier expression and rearranging the formula, we get:
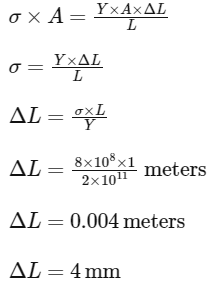
Thus, the maximum elongation of the wire within the elastic limit is
The answer is: Option A - 4 mm.
Q2: A metallic bar of Young's modulus, 0.5 × 1011 Nm−2 and coefficient of linear thermal expansion 10−5∘C−1, length 1 m and area of cross-section 10−3 m2 is heated from 0∘C to 100∘C without expansion or bending. The compressive force developed in it is :
(a) 5 x 103 N
(b) 50 x 103 N
(c) 100 x 103 N
(d) 2 x 103 N [2024]
Ans: (b)
Given the properties and conditions of the metallic bar, we are required to calculate the compressive force developed due to heating. Key inputs include the Young's modulus (E), coefficient of linear thermal expansion (α), change in temperature (ΔT), and the original dimensions of the bar.
First, compute the linear expansion of the bar if it were free to expand. The change in length (ΔL) due to thermal expansion can be computed through the formula: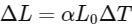
Given:
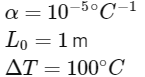
Thus:
This is the change in length that the bar would undergo if not constrained.
However, in this scenario, the bar is constrained and does not actually expand. This constraint induces a compressive stress (constrained thermal stress) in the bar, which can be calculated using the formula relating stress, Young's modulus, and strain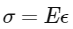
Where the strain (ε) under constrained conditions due to thermal expansion is:
Therefore:
This stress is the force per unit area. To find the compressive force, we need to multiply this stress by the cross-sectional area of the bar: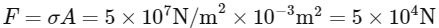
Thus, the compressive force developed in the bar is
Hence, the correct answer is Option B:
Q3: A thin flat circular disc of radius 4.5cm is placed gently over the surface of water. If surface tension of water is 0.07Nm-1, then the excess force required to take it away from the surface is
(a) 19.8 mN
(b) 198 N
(c) 1.98 mN
(d) 99 N
Ans: (a)
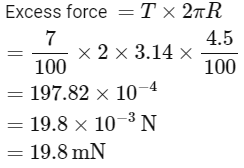
2023
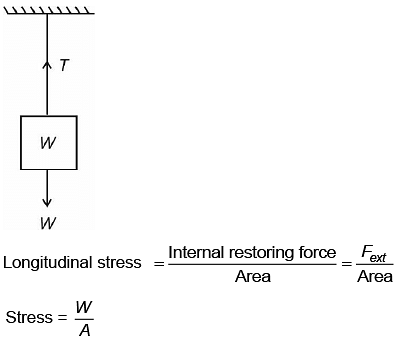
Q1: Let a wire be suspended from the ceiling (rigid support) and stretched by a weight W attached at its free end. The longitudinal stress at any point of cross-sectional area A of the wire is [2023]A: 2W/A
B: W/A
C: W/2A
D: Zero
Ans: B
2022
Q1: Given below are two statements: One is labelled as Assertion (A) and the other is labelled as Reason (R).
Assertion (A): The stretching of a spring is determined by the shear modulus of the material of the spring.
Reason (R): A coil spring of copper has more tensile strength than a steel spring of same dimensions. In the light of the above statements, choose the most appropriate answer from the options given below [2022]
A: Both (A) and (R) are true and (R) is not the correct explanation of (A)
B: (A) is true but (R) is false
C: (A) is false but (R) is true
D: Both (A) and (R) are true and (R) is the correct explanation of (A)
Ans: B
It is true that the stretching of spring is determined by shear modulus of the spring as when coil spring is stretched neither its length nor its volume changes, there is only change in its shape. The tensile strength of steel is more than that of copper. Hence Assertion is true and reason is false.
2020
Q1: Dimensions of stress are : [2020]
A: [ML0T–2]
B: [ML–1T–2]
C: [MLT–2]
D: [ML2T–2]
Ans: B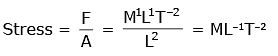
Q2: A wire of length L, area of cross-section A is hanging from a fixed support. The length of the wire changes to L1 when mass M is suspended from its free end. The expression for Young's modulus is : [2020]
A: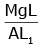
B: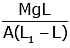
C: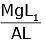
D: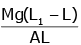
Ans: B
from young’s modulus formula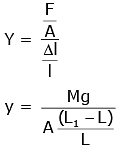
2019
Q1: When a block of mass M is suspended by a long wire of length L, the length of the wire becomes (L + l). The elastic potential energy stored in the extended wire is: [2019]
A: Mgl
B: MgL
C: 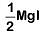
D: 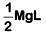
Ans: C
Solution:
Given:
- Original length of the wire
- Extended length L+l, so the extension is l.
- Mass of the block M, so the force exerted by the block due to gravity is F=Mg, where g is the acceleration due to gravity.
Step 1: Determine the Force Acting on the Wire
The force acting on the wire due to the suspended block is equal to the weight of the block: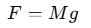
Step 2: Calculate the Elastic Potential Energy
The elastic potential energy U stored in a stretched wire (or spring) with an extension l is given by:
2018
Q1: Two wires are made of the same material and have the same volume. The first wire has cross-sectional area A and the second wire has cross-sectional area 3A. If the length of the first wire is increased by Δl on applying a force F, how much force is needed to stretch the second wire by the same amount ? [2018]
A: 9F
B: 6F
C: 4F
D: F
Ans: A
Solution: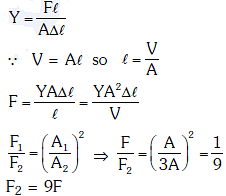
2017
Q1: The bulk modulus of a spherical object is 'B'. If it is subjected to uniform pressure 'p', the fractional decrease in radius is:- [2017]
A: 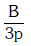
B: 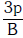
C: 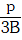
D: 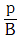
Ans: C
Solution:
2014
Q1: Copper of fixed volume ‘V’ is drawn into wire of length ‘l’. When this wire is subjected to a constant force ‘F’, the extension produced in the wire is ‘Δl’. Which of the following graphs is straight line? [2014]
A: Δl versus l/l2
B: Δl versus l
C: Δl versus l/l
D: Δl versus l2
Ans: D
Solution: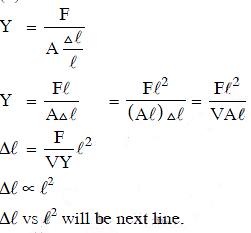
There is no Question for NEET 2021
|
97 videos|378 docs|103 tests
|
FAQs on NEET Previous Year Questions (2014-2024): Mechanical Properties of Solids - Physics Class 11
| 1. What are the different mechanical properties of solids? |  |
| 2. How are mechanical properties of solids important in material science? |  |
| 3. What is the difference between hardness and toughness in terms of mechanical properties of solids? |  |
| 4. How does temperature affect the mechanical properties of solids? |  |
| 5. Can you explain the concept of elasticity in terms of mechanical properties of solids? |  |

|
Explore Courses for NEET exam
|

|


















