NEET Previous Year Questions (2014-24): Thermal Properties of Matter | Physics Class 11 PDF Download
2024
Q1: The following graph represents the T-V curves of an ideal gas (where T is the temperature and V the volume) at three pressures P1,P2 and P3 compared with those of Charles's law represented as dotted lines. [2024]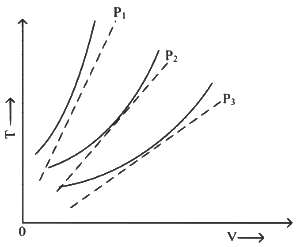 Then the correct relation is :
Then the correct relation is :(a) P3 > P2> P1
(b) P1 > P3 > P2
(c) P2 > P1 > P3
(d) P1 > P2 > P3
Ans: (d) P1 > P2 > P3
Explanation:
At same temperature, curve with higher volume corresponds to lower pressure.
(We draw a straight line parallel to volume axis to get this)
2022
Q1: The energy that will be ideally radiated by a 100 kW transmitter in 1 hour is
(a) 36 × 104 J
(b) 36 × 105 J
(c) 1 × 105 J
(d) 36 × 107 J [2022]
Ans: (d) 36 × 107 J
Explanation:
Given:
- Power of the transmitter, P = 100 kW = 100 × 10³ W
- Time, t = 1 hour = 3600 seconds
The energy radiated is calculated using the formula:
Energy (E) = Power (P) × Time (t)Substitute the given values:
E = (100 × 10³) × 3600Simplify:
E = 36 × 10⁷ JFinal Answer: (d) 36 × 10⁷ J
2021
Q1: A cup of coffee cools from 90°C to 80°C in t minutes, when the room temperature is 20°C. The time taken by a similar cup of coffee to cool from 80°C to 60°C at room temperature same at 20°C. [2021]
(a) 10/13t
(b) 5/13t
(c) 13/10t
(d) 13/5t
Ans: (d) 13/5 t
Explanation:
According to Newton's law of cooling:T1 - T2t = K (T1 + T2)2 - T0
For the 1st cup of coffee:90 - 80t = K (90 + 80)2 - 20 ....(1)
For the 2nd cup of coffee:80 - 60t' = K (80 + 60)2 - 20 ....(2)
Divide equation (1) by equation (2):t't = 6550
⇒ t' = 135 t
2020
Q1: The quantities of heat required to raise the temperature of two solid copper spheres of radii r1 and r2 (r1 = 1.5 r2) through 1 K are in the ratio: [2020]
(a) 3 : 2
(b) 5 : 3
(c) 27 : 8
(d) 9 : 4
Ans: (c) 27/8
Explanation:
We know that heat required,
Q = msΔT = 43 πr³ × ρ × sΔT
[∵ mass = density × volume]
For same material and for same temperature change:
Q ∝ r³ .......(1)
So, Q1Q2 = (r1)³(r2)³
Substituting the given data, we get:
Q1Q2 = (1.5 r2)³r2³ = 278
⇒ Q1 : Q2 = 27 : 8
2019
Q1: A copper rod of 88 cm and an aluminium rod of unknown length have their increase in length independent of increase in temperature. The length of aluminium rod is: [2019]
(αCu = 1.7 × 10-5 K-1 and αAl = 2.2 × 10-5 K-1)
(a) 6.8 cm
(b) 113.9 cm
(c) 88 cm
(d) 68 cm
Ans: (d) 68 cm
Explanation:
CONCEPT:
The change in the length of any rod is due to the thermal expansion, and it is written as:
α = 1T Δl / ΔT ....(1)
Here, Δl is the change in the length, ΔT the change in temperature, α is the thermal expansion, and L is the length of the rod.
CALCULATION:
Given:
- The thermal expansion of copper rod, αCu = 1.7 × 10-5 K-1
- The thermal expansion of aluminum rod, αAl = 2.2 × 10-5 K-1
- Length of copper rod, LAl = 88 cm
Here it is given that an aluminum rod of unknown length has an increase in length independent of an increase in temperature. Therefore, we can write from equation (1):
αCu × LCu = αAl × LAl
1.7 × 10-5 × 88 cm = 2.2 × 10-5 × LAl
⇒ 1.7 × 882.2 = LAl
⇒ LAl = 68 cm
2018
Q1: The power radiated by a black body is P and it radiates maximum energy at wavelength 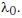 If the temperature of the black body is now changed so that it radiates maximum energy at wavelength
If the temperature of the black body is now changed so that it radiates maximum energy at wavelength 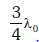 , the power radiated by it becomes nP. The value of n is:- [2018]
, the power radiated by it becomes nP. The value of n is:- [2018]
(a) 3/4
(b) 4/3
(c) 256/81
(d) 81/256
Ans: (c)
Explanation:
P = σAT⁴ ⇒ P ∝ T⁴
According to Wein's law, T ∝ 1λm
⇒ P ∝ ( 1λm)⁴
⇒ P2P1 = ( λm1λm2)⁴
⇒ P2P1 = ( λ034λ0)⁴
⇒ nPP = 25681 ⇒ n = 25681
2017
Q1: A spherical black body with a radius of 12 cm radiates 450 watt power at 500 K. If the radius were halved and the temperature doubled, the power radiated in watt would be:- [2017]
(a) 450
(b) 1000
(c) 1800
(d) 225
Ans: (d) 1800
Explanation:
The energy radiated per second by a black body is given by Stefan's Law as:
Et = σT⁴ × A
where A is the surface area of the black body.
For a sphere, A = 4πr²:
Et = σT⁴ × 4πr²
Case (i):
Given:
- E/t = 450
- T = 500K
- r = 0.12m
Substituting into the equation:
450 = 4πσ(500)⁴(0.12)² ....(i)Case (ii):
Given:
- E/t = ?
- T = 1000K
- r = 0.06m
Dividing (ii) by (i), we get:
E/t450 = (1000)⁴ × (0.06)²(500)⁴ × (0.12)²
Simplifying:
E/t450 = 2⁴1 = 4
⇒ E/t = 450 × 4 = 1800W
(d) is the correct option.
Q2: Two rods A and B of different materials are welded together as shown in figure. Their thermal conductivities are K1 and K2. The thermal conductivity of the composite rod will be:- [2017]
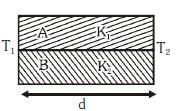
(a) 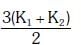
(b) K1 + K2
(c) 2(K1 + K2)
(d) 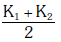
Ans: (d) 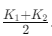
Explanation:
Concept:
When two rods with different thermal conductivities are placed in series (end-to-end), the equivalent thermal conductivity Keq of the composite rod can be calculated using the formula for thermal conductivity in series:
1Keq = d1K1 + d2K2
Where d1 and d2 are the lengths of the respective rods.
However, when the rods are placed side by side, as shown in the figure, the thermal conductivities act in parallel. The equivalent thermal conductivity for parallel conduction is:
Keq = K1 + K22
This formula applies since the rods are assumed to have the same cross-sectional area.
Solution
For the rods placed side by side as in the figure, the effective thermal conductivity is the average of the two conductivities:
Keq = K1 + K22
Thus, the correct answer is: (d) K1 + K22
2016
Q1: Coefficient of linear expansion of brass and steel rods are α1 and α2 . Lengths of brass and steel rods are ℓ1 and ℓ2 respectively. If (ℓ2 - ℓ1 ) is maintained same at all temperatures, which one of the following relations holds good ? [2016]
(a) α1ℓ1 = α2ℓ2
(b) α1ℓ2 = α2ℓ1
(c) α1ℓ22 = α2ℓ12
(d) α12ℓ2 = α22ℓ1
Ans: (a) α1ℓ1 = α2ℓ2
Explanation:
Coefficient of linear expansion of brass = α1
Coefficient of linear expansion = α2
Length of brass and steel rods are l1 and l2 respectively.
Given,
Increase in length (l2'-l1' ) is same for all temperature.
So,'l2 - l1' = l2 - l1
⇒ l2(1 + α2Δt) - l1(1 + α1Δt) = l2 - l1
⇒ l2α2 = l1α1
Q2: A piece of ice falls from a height h so that it melts completely. Only one-quarter of the heat produced is absorbed by the ice and all energy of ice gets converted in to heat during its fall. The value of h is : [Latent heat of ice is 3.4 x 105 J/Kg and g = 10 N/kg] [2016]
(a) 68 km
(b) 34 km
(c) 544 km
(d) 136 km
Ans: (d) 136 Km
Explanation:
Given:
- Latent heat of ice (L) = 3.4 × 10⁵ J/kg
- Gravitational acceleration (g) = 10 N/kg
- Only one-quarter of the heat produced is absorbed by the ice.
Let h be the height from which the ice falls.
The energy produced due to the fall is given by:
Potential energy = m × g × hOnly one-quarter of this energy is absorbed by the ice:
Energy absorbed by ice = (1/4) × m × g × hThe energy required to melt the ice completely is:
Q = m × LEquating the energy absorbed by the ice to the energy required to melt it:
(1/4) × m × g × h = m × LCanceling m from both sides:
(1/4) × g × h = LSubstitute the given values:
(1/4) × 10 × h = 3.4 × 10⁵Simplify:
2.5 × h = 3.4 × 10⁵Solve for h:
h = (3.4 × 10⁵) / 2.5
h = 1.36 × 10⁵ metersConvert meters to kilometers:
h = 136 kilometers
Q3: A block body is at a temperature of 5760 K. The energy of radiation emitted by the body at wavelength 250 nm is U1 at wavelength 500 nm is U2 and that at 1000 nm is U3. Wien's constant, b = 2.88 x 106 nmK. Which of the following is correct? [2016]
(a) U1 > U2
(b) U1 = 0
(c) U3 = 0
(d) U2 > U1
Ans: (d) U2 > U1
Explanation:
Given, temperature, T1 = 5760 K
Given that energy of radiation emitted by the body at wavelength 250 nm in U1, at wavelength 500 nm is U2 and that at 1000 nm is U3.
Now, according to Wein's law, we get
λm T = b
where, b = Wien's constant = 2.88 × 106 nmK
⇒ λm = bT
⇒ λm = 2.88 × 106 nmK5760 K
⇒ λm = 500 nmλm is the wavelength corresponding to maximum energy, so U2 > U1.
Q4: Two identical bodies are made of a material for which the heat capacity increases with temperature. One of these is at 100°C, while the other one is at 0°C. If the two bodies are brought into contact, then, assuming no heat loss, the final common temperature is [2016]
(a) 50°C
(b) more than 50°C
(c) less than 50°C but greater than 0°C
(d) 0°C
Ans: (b) more than 50°C
Explanation:
Since, heat capacity of material increases with increase in temperature so, body at 100°C has more heat capacity than body at 0°C. Hence, final common temperature of the system will be closer to 100°C.
∴ Tc > 50°C
Q5: A body cools from a temperature 3T to 2T in 10 minutes. The room temperature is T. Assume that Newton’s law of cooling is applicable. The temperature of the body at the end of next 10 minutes will be [2016]
(a) 7/4T
(b) 3/2T
(c) 4/3T
(d) T
Ans: (b) 3/2T
Explanation:
According to Newton’s law of cooling,dTdt = K(T - Ts)
For two cases:
dT1dt = K(T1 - Ts) and dT2dt = K(T2 - Ts)
Here, Ts = T,
T1 = 3T + 2T2 = 2.5T
dT1dt = 3T - 2T10 = T10
T2 = 2T + T'2 and dT2dt = 2T - T'10
So:
T10 = K(2.5T - T) ....(i)
2T - T'10 = K (2T + T')2 - T ....(ii)
Dividing eqn. (i) by eqn. (ii), we get:
T2T - T' = 2.5T - T2T + T'2 - T
or, 2T + T'2 = (2T - T') × 32
T' = 3(2T - T') or, 4T' = 6T; ∴ T' = 32T
2015
Q1: The two ends of a metal rod are maintained at temperatures 100oC and 110oC. the rate of heat flow in the rod is found to be 4.0 J/s. If the ends are maintained at temperatures 200oC and 210oC, the rate of heat flow will be: [2015]
(a) 4.0 J/s
(b) 44.0 J/s
(c) 16.8 J/s
(d) 8.0 J/s
Ans: (a) 4.0 J/s
Explanation:
Concept:
When there is a temperature difference between two points, heat flow occurs from higher temperatures to lower temperatures. This phenomenon is called heat transfer.dQdt = k A dTdx
Where:
- dQ/dt = rate of heat transfer
- k = constant
- A = area
- dT/dx = rate of temperature gradient
Explanation:
Given:
- Case 1: T1 = 100°C, T2 = 110°C, ΔT = 10°C, rate of heat flow = 4 J/s.
- Case 2: T1 = 200°C, T2 = 210°C, ΔT = 10°C.
As the temperature difference and length of the rod are constant, the heat flow will remain constant.
So, the value of heat flow in case 2 will also be equal to 4 J/s.
Q2: The value of coefficient of volume expansion of glycerin is 5 ×10–4 K–1. The fractional change in the density of glycerin for a rise of 40°C in its temperature, is [2015]
(a) 0.025
(b) 0.010
(c) 0.015
(d) 0.020
Ans: (d) 0.020
Explanation:
Let ρ0 and ρT be densities of glycerin at 0°C and T °C respectively. Then,
ρT = ρ0(1 - γΔT)where γ is the coefficient of volume expansion of glycerine and ΔT is the rise in temperature.
ρTρ0 = 1 - γΔT or γΔT = 1 - ρTρ0
Thus, ρ0 - ρTρ0 = γΔT
Here:
- γ = 5 × 10-4 K-1
- ΔT = 40°C = 40 K
∴ The fractional change in the density of glycerine:
ρ0 - ρTρ0 = γΔT = (5 × 10-4 K-1)(40 K) = 0.020
Q3: On observing light from three different stars P, Q and R, it was found that intensity of violet colour is maximum in the spectrum of P, the intensity of green colour is maximum in the spectrum of R and the intensity of red colour is maximum in the spectrum of Q. If TP, TQ and TR are the respective absolute temperatures of P, Q and R, then it can be concluded from the above observations that: [2015]
(a) TP < TQ < TR
(b) TP > TQ > TR
(c) TP > TR > TQ
(d) TP < TR < TQ
Ans: (b) TP > TQ > TR
Explanation:
According to Wien's law:
λ ∝ 1T and λV < λG < λR
∴ TP > TQ > TR
2014
Q1: Light with an energy flux of 25 x 104Wm−2 falls on a perfectly reflecting surface at normal incidence. If the surface area is 15 cm2, the average force exerted on the surface is [2014]
(a) 1.20 x 10−6 N
(b) 3.0 x 10−6 N
(c) 1.25 x 10−6 N
(d) 2.50 x 10−6 N
Ans: (d) 2.50 x 10−6 N
Explanation:
Step 1: Use the Formula for Radiation Pressure on a Perfectly Reflecting SurfaceFor a perfectly reflecting surface, the radiation pressure P is given by:
P = 2Ic
where:
- I is the energy flux
- c is the speed of light in vacuum, c = 3 × 108 m/s
Step 2: Find the Radiation Pressure
Substitute the given energy flux into the formula:
P = 2 × 25 × 1043 × 108
P = 50 × 1043 × 108
P = 503 × 10-4 N/m2
P = 16.67 × 10-4 N/m2
Step 3: Find the Force Exerted
The force F exerted on the surface is given by:
F = P × A
Substitute the values for P and A:
F = (16.67 × 10-4) × (15 × 10-4) N
F = 250.05 × 10-8 N
F = 2.50 × 10-6 N
Q2: Certain quantity of water cools from 70°C to 60°C in the first 5 minutes and to 54° C in the next 5 minutes. The temperature of the surroundings is [2014]
(a) 42°C
(b) 10°C
(c) 45°C
(d) 20°C
Ans: (c) 45°C
Explanation:
Newton's Law of Cooling:dTdt = -k(T - Tsurroundings)
Where:
- T is the temperature of the object
- Tsurroundings is the temperature of the surroundings
- k is a constant
- dTdt is the rate of change of temperature
The cooling of the water from 70°C to 60°C takes the same time as from 60°C to 54°C. We can use this information to estimate the temperature of the surroundings.
Step 1: Average temperature during each time interval
- From 70°C to 60°C:
- Average temperature T1 = 70 + 602 = 65°C
- From 60°C to 54°C:
- Average temperature T2 = 60 + 542 = 57°C
Step 2: Ratio of temperature drops
The temperature difference between the water and the surroundings governs the rate of cooling.
Let Ts be the temperature of the surroundings. According to Newton's Law of Cooling, the temperature drop is proportional to the difference in temperature between the water and the surroundings:
(70 - 60)(60 - 54) = (65 - Ts)(57 - Ts)
106 = 65 - Ts57 - Ts
Step 3: Solving the equation
Cross-multiply:
10(57 - Ts) = 6(65 - Ts)
Expand:
570 - 10Ts = 390 - 6Ts
Simplify:
570 - 390 = 10Ts - 6Ts
180 = 4Ts
Solve for Ts:
Ts = 1804 = 45°C
Q3: Steam at 100°C is passed into 20 g of water at 10°C. When water acquires a temperature of 80°C, the mass of water present will be:
[Take specific heat of water = 1 cal g−1 °C−1 and latent heat of steam = 540 cal g−1] [2014]
(a) 42.5 g
(b) 22.5 g
(c) 24 g
(d) 31.5 g
Ans: (b) 22.5 g
Explanation:
Step 1: Heat required to raise the temperature of water from 10°C to 80°CGiven:
- Mass of water = 20 g
- Initial temperature of water = 10°C
- Final temperature of water = 80°C
- Specific heat of water = 1 cal/g°C
The heat required to raise the temperature of water is:
Qwater = mwater × specific heat of water × ΔT
Qwater = 20 × 1 × (80 - 10) = 20 × 70 = 1400 cal
Step 2: Heat lost by the steam during condensation
The latent heat of steam is given as 540 cal/g. Let the mass of steam condensed be msteam.
The heat released by steam upon condensation is:
Qsteam = msteam × latent heat of steam
Qsteam = msteam × 540
Step 3: Heat released by condensed steam to cool down from 100°C to 80°C
The condensed steam (now water) will also release some heat as it cools down from 100°C to 80°C. This heat is given by:
Qcooling = msteam × specific heat of water × ΔT
Qcooling = msteam × 1 × (100 - 80) = msteam × 20
Step 4: Total heat lost by steam
The total heat lost by steam is:
Qtotal = Qsteam + Qcooling = msteam × 540 + msteam × 20 = msteam × 560
Step 5: Using the principle of conservation of energy
The heat gained by water is equal to the heat lost by the steam:
1400 = msteam × 560
Solve for msteam:
msteam = 1400560 = 2.5 g
Step 6: Total mass of water present
The mass of the water initially present was 20 g, and the steam condensed to form 2.5 g of water. Therefore, the total mass of water is:
Total mass of water = 20 g + 2.5 g = 22.5 g
|
97 videos|379 docs|103 tests
|
FAQs on NEET Previous Year Questions (2014-24): Thermal Properties of Matter - Physics Class 11
| 1. What are the key concepts of thermal properties of matter relevant for NEET? |  |
| 2. How does specific heat capacity affect temperature change in substances? |  |
| 3. What is the difference between conduction, convection, and radiation? |  |
| 4. How do you calculate the heat transfer in calorimetry experiments? |  |
| 5. What role does thermal expansion play in engineering applications? |  |




















