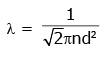NEET Previous Year Questions (2014-2025): Kinetic Theory | Physics Class 11 PDF Download
2025
Q1: A container has two chambers of volumes V1 = 2 litres and V2 = 3 litres separated by a partition made of a thermal insulator. The chambers contains n1 = 5 and n2 = 4 moles of ideal gas at pressures p1 = 1 atm p2 = 2 atm, respectively. When the partition is removed, the mixture attains an equilibrium pressure of: [2024]
(a) 1.4 atm
(b) 1.8 atm
(c) 1.3 atm
(d) 1.6 atm
Ans: (d)
Before partition
after partition removed
P1V1 + P2V2 = P(V1 + V2)
⇒ 1 × 2 + 2 × 3 = P × (2 + 3)
⇒ 8 / 5 = P
⇒ P = 1.6 atm
Q2: An oxygen cylinder of volume 30 litre has 18.20 moles of oxygen. After some oxygen is withdrawn from the cylinder, its gauge pressure drops to 11 atmospheric pressure at temperature 27°C. The mass of the oxygen withdrawn from the cylinder is nearly equal to:
[Given, R = 100/12 J mol-1 K-1, and molecular mass of O2 = 32, 1 atm pressure = 1.01 x 105 N/m] [2024]
(a) 0.116 kg
(b) 0.156 kg
(c) 0.125 kg
(d) 0.144 kg
Ans: (a)
Number of moles left
n = PV / RT = (12 × 1.01 × 105 N/m2 × 30 × 10−3 m3) / ((100/12) × 300)
n = (12 × 1.01 × 12) / 10 = 14.54 moles
Moles removed = 18.2 − 14.54
= 3.656 moles
Mass removed = 3.656 × 32 = 116.99 g = 0.116 kg
2024
Q1: The following graph represents the T - V curves of an ideal gas (where T is the temperature and V the volume) at three pressures P1, P2 and P3 compared with those of Charles's law represented as dotted lines. [2024]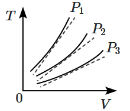 Then the correct relation is :
Then the correct relation is :
(a) P1 > P3 > P2
(b) P2 > P1 > P3
(c) P1 > P2 > P3
(d) P3 > P2 > P1
Ans: (c)
In the graph showing the T-V (temperature vs. volume) curves for an ideal gas at three different pressures P1, P2, and P3:
- According to Charles's Law, for an ideal gas, temperature is directly proportional to volume at constant pressure (T ∝ V).
- At higher pressure, the curve will be closer to the origin, meaning that for the same volume, the temperature is higher. This is because the gas is more compressed at higher pressure.
- At lower pressure, the curve will be further from the origin, meaning that for the same volume, the temperature is lower.
So, the pressure with the highest curve corresponds to the highest temperature, and the pressure with the lowest curve corresponds to the lowest temperature.
Conclusion:
The correct relation between the pressures is P1 > P2 > P3.Final Answer: (c) P1 > P2 > P3.
Q2: An ideal gas at 0∘C and atmospheric pressure P has volume V. The percentage increase in its temperature needed to expand it to 3V at constant pressure is: [2024]
(a) 100%
(b) 200%
(c) 300%
(d) 50%
Ans: (b)
Charles's Law states that the volume of an ideal gas is directly proportional to its temperature when pressure is constant.
The formula is:
(V1 / T1) = (V2 / T2)
Where:
- V1 is the initial volume,
- T1 is the initial temperature in Kelvin,
- V2 is the final volume,
- T2 is the final temperature in Kelvin.
Apply the given values
- Initial volume V1 = V,
- Initial temperature T1 = 273 K (0°C),
- Final volume V2 = 3V.
Using the formula:
V / 273 = 3V / T2
Solve for T2:
T2 = 3 × 273 = 819 K.
The temperature increase is:
ΔT = T2 - T1 = 819 K - 273 K = 546 K.
The percentage increase in temperature is:
Percentage increase = (ΔT / T1) × 100 = (546 / 273) × 100 = 200%.
Final Answer: (b) 200%.
Q3: The equilibrium state of a thermodynamic system is described by:
A. Pressure
B. Total heat
C. Temperature
D. Volume
E. Work done
Choose the most appropriate answer from the options given below: [2024]
(a) A, B and E only
(b) B, C and D only
(c) A, B and C only
(d) A, C and D only
Ans: (d)
The equilibrium state of a thermodynamic system is characterized by conditions that define its state. These conditions typically include parameters that describe the system's state at a given time and ensure that it is in equilibrium (no net change in state).
The correct parameters to describe the equilibrium state of a system are:
- Pressure (A): Pressure is a key factor in determining the equilibrium state, as it helps define the balance of forces within the system.
- Temperature (C): Temperature is also crucial in defining the equilibrium state, as it determines the energy distribution within the system.
- Volume (D): Volume is important in describing the spatial configuration of the system in equilibrium, as the system's volume directly impacts its state.
The other options like Total heat (B) and Work done (E) are not sufficient alone to describe the equilibrium state, as they depend on the path taken and are not state functions.
Final Answer: (d) A, C and D only.
Q4: According to the law of equipartition of energy, the number of vibrational modes of a polyatomic gas of constant γ = Cp / Cv is (where Cp and Cv are the specific heat capacities of the gas at constant pressure and constant volume, respectively): [2024]
(a) (4 + 3γ) / (γ − 1)
(b) (3 + 4γ) / (γ − 1)
(c) (4 - 3γ) / (γ − 1)
(d) (3 - 4γ) / (γ − 1)
Ans: (c)
For a polyatomic gas, the degrees of freedom include:
- 3 translational degrees of freedom (movement in x, y, and z directions),
- 3 rotational degrees of freedom (rotation about 3 axes),
- Vibrational modes, where each vibration contributes 2 degrees of freedom (1 for potential energy and 1 for kinetic energy).
- The specific heat at constant volume, Cv, is related to the number of degrees of freedom by the equation: Cv = (f / 2) R, where f is the total number of degrees of freedom and R is the gas constant.
- The specific heat ratio γ is defined as γ = Cp / Cv, where Cp is the specific heat at constant pressure.
- The total number of degrees of freedom, f, for a polyatomic gas is: f = 3 (translational) + 3 (rotational) + 2v (vibrational), where v is the number of vibrational modes.
- The relationship between γ and f is given by γ = (f + 2) / f.
- Solving this equation for f, we get f = 2 / (γ - 1).
- From the total degrees of freedom f = 6 + 2v, substitute f = 2 / (γ - 1) into this equation: 6 + 2v = 2 / (γ - 1).
- Solving for v, we get v = (4 - 3γ) / (γ - 1).
Final Answer: (c) (4 - 3γ) / (γ - 1).
2023
Q1: The temperature of a gas is –50°C. To what temperature the gas should be heated so that the rms speed is increased by 3 times? [2023]
(a) 669°C
(b) 3295°C
(c) 3097 K
(d) 223 K
Ans: (b) 3295°C
Explanation:
The root mean square (RMS) speed vrms of a gas is given by the equation:
vrms = √ 3RTm
vrms ∝ √T
T1 = 273 - 50 = 223 K
vrms is increased by 3 times
T2 = ?So, final RMS speed = v + 3v = 4v
v4v = √ T1T2
√ 116 = √ 223T2
T2 = 3568 K
T2 = 3568 - 273 = 3295°C
Q2: A container of volume 200 cm3 contains 0.2 mole of hydrogen gas and 0.3 mole of argon gas. The pressure of the system at temperature 200 K ( R = 8.3 JK–1 mol–1) will be: [2023]
(a) 6.15 × 105 Pa
(b) 6.15 × 104 Pa
(c) 4.15 × 105 Pa
(d) 4.15 × 106 Pa
Ans: (d)
Given the volume is 200 cm³, we need to convert it to cubic meters:
1 cm³ = 1 × 10⁻⁶ m³, so: 200 cm³ = 200 × 10⁻⁶ m³ = 2 × 10⁻⁴ m³.The total number of moles in the container is the sum of the moles of hydrogen gas and argon gas:
- Moles of hydrogen gas = 0.2 moles,
- Moles of argon gas = 0.3 moles.
Total number of moles = 0.2 + 0.3 = 0.5 moles.
Now, we can substitute the values into the ideal gas law:P × V = n × R × T
Substitute the values:
- P = pressure (which we need to find),
- V = 2 × 10⁻⁴ m³,
- n = 0.5 moles,
- R = 8.3 J/K·mol,
- T = 200 K.
So, the equation becomes:
P × 2 × 10⁻⁴ = 0.5 × 8.3 × 200
Solve for P:
P = (0.5 × 8.3 × 200) / (2 × 10⁻⁴)
P = (830) / (2 × 10⁻⁴)
P = 4.15 × 10⁶ Pa
Final Answer: (d) 4.15 × 10⁶ Pa.
2021
Q1: Match column - I and column - II and choose the correct match from the given choices. [2021]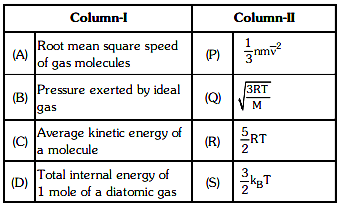
(a) (A) - (Q), (B) - (P), (C) - (S), (D) - (R)
(b) (A) - (R), (B) - (Q), (C) - (P), (D) - (S)
(c) (A) - (R), (B) - (P), (C) - (S), (D) - (Q)
(d) (A) - (Q), (B) - (R), (C) - (S), (D) - (P)
Ans: (a) (A) - (Q), (B) - (P), (C) - (S), (D) - (R)
Explanation:
(A) Root mean square speed of gas molecules:Root mean square (RMS) speed of gas molecules is given by the formula:
vrms = √ 3RTMHence, it matches with (Q).
(B) Pressure exerted by an ideal gas:The pressure exerted by an ideal gas can be represented using:
P = 13 mv2Hence, it matches with (P).
(C) Average kinetic energy of a molecule:The average kinetic energy per molecule is given by:
E = 32 kBTHence, it matches with (S).
(D) Total internal energy of 1 mole of a diatomic gas:The total internal energy for one mole of a diatomic gas is:
U = 52 RTHence, it matches with (R).
2020
Q1: A cylinder contains hydrogen gas at pressure of 249 kPa and temperature 27°C.
Its density is : (R = 8.3 J mol-1 K-1) [2020]
(a) 0.1 kg/m3
(b) 0.02 kg/m3
(c) 0.5 kg/m3
(d) 0.2 kg/m3
Ans: (d) 0.2 kg/m3
The ideal gas equation represents the state of a gas and provides a good approximation of its behavior under certain conditions. It is expressed as:
PV = nRT
Where:
- P is the pressure,
- V is the volume,
- n is the number of moles of the gas,
- R is the universal gas constant, and
- T is the temperature.
Using the ideal gas equation, we have:
PV = mM RT ⟹ ρV = m ⟹ m = ρV
PV = (ρV)RTM
ρ = PMRT
Substituting the values:
ρ = 249 × 103 × 2 × 10–38.3 × 300 = 0.2 kg/m3
Q2: The mean free path for a gas, with molecular diameter d and number density n can be expressed as : [2020]
(a)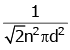
(b) 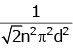
(c)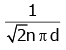
(d)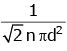
Ans: (d) 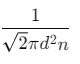
Explanation:
The mean free path for gas is given by
Q3: The average thermal energy for a mono-atomic gas is (kB is Boltzmann constant and T, absolute temperature) [2020]
(a) 1/2kBT
(b) 3/2kBT
(c) 5/2kBT
(d) 7/2kBT
Ans: (b) 3/2kBT
Thermal energy refers to the energy present within a system that is responsible for its temperature.
Thermal energy is given by the relation:
ΔET = μk F d
Where:
- μk – Coefficient of friction
- F – Force
- d – Distance
For mono-atomic gas, the total degree of freedom = 3 (translational degrees of freedom), i.e., rotational, vibrational, and translational.
The average thermal energy for a mono-atomic gas (U) is given as:
U = (total degree of freedom) × 12 KBT
By putting the value of the degree of freedom, we get:
U = 32 KBT
Hence, the average thermal energy for a mono-atomic gas is:
U = 32 KBT
2019
Q1: Increase in temperature of a gas filled in a container would lead to: [2019]
(a) Increase in its mass
(b) Increase in its kinetic energy
(c) Decrease in its pressure
(d) Decrease in intermolecular distance
Ans: (b) Increase in its kinetic energy
(a) Increase in its mass: The mass of the gas remains constant as temperature changes; it is not affected by temperature.
(b) Increase in its kinetic energy: As the temperature of the gas increases, the kinetic energy of the gas molecules increases because the molecules move faster at higher temperatures.
(c) Decrease in its pressure: An increase in temperature would actually lead to an increase in pressure (if the volume is constant), not a decrease.
(d) Decrease in intermolecular distance: The intermolecular distance usually increases when the temperature rises because gas molecules move faster and spread out more.
2018
Q1: At what temperature will the rms speed of oxygen molecules become just sufficient for escaping from the Earth's atmosphere ? (Given: Mass of oxygen molecule (m) = 2.76 × 10–26 kg Boltzmann's constant kB = 1.38 × 10–23 J K–1):- [2018]
(a) 2.508 × 104 K
(b) 8.360 × 104 K
(c) 5.016 × 104 K
(d) 1.254 × 104 K
Ans: (b) 8.360 × 104 K
Explanation:
Mass of oxygen molecule (m) = 2.76 × 10-26 kg
Boltzmann's constant (kB) = 1.38 × 10-23 J·K-1
Escape velocity (Vescape) = 11200 m/s
Say at temperature T, it attains Vescape.
√ 3kBTmO2 = 11200 m/s
On solving,
T = 8.360 × 104 K
2017
Q1: A gas mixture consists of 2 moles of O2 and 4 moles of Ar at temperature T. Neglecting all vibrational modes, the total internal energy of the system is:- [2017]
(a) 15 RT
(b) 9 RT
(c) 11 RT
(d) 4 RT
Ans: (c)
Explanation:
For O2 (diatomic gas):
- Oxygen (O2) is a diatomic gas. For diatomic gases, the internal energy per mole is given by:
UO2 = 52 RT per mole
- For 2 moles of O2:
UO2 = 2 × 52 RT = 5RT
For Ar (monatomic gas):
- Argon (Ar) is a monatomic gas. For monatomic gases, the internal energy per mole is given by:
UAr = 32 RT per mole
- For 4 moles of Ar:
UAr = 4 × 32 RT = 6RT
Total Internal Energy of the System:
The total internal energy is the sum of the internal energy of O2 and Ar:
Utotal = UO2 + UAr = 5RT + 6RT = 11RT
Thus, the total internal energy of the system is 11RT.
2016
Q1: The molecules of a given mass of a gas have r.m.s. velocity of 200 ms-1 at 27°C and 1.0 x 10-5 Nm-2 pressure. When the temperature and pressure of the gas are respectively, 127°C and 0.05 x 105Nm2, the r.m.s. velocity of velocity of its molecules in ms-1 is; [2016]
(a) 100 / 3
(b) 100 √2
(c) 400 / √3
(d) 100√2 / 3
Ans: (c)
Explanation:The root mean square (r.m.s.) velocity (vrms) of a gas is given by:
vrms ∝ √T
This means that the r.m.s. velocity is proportional to the square root of the absolute temperature of the gas.
Given that the initial r.m.s. velocity vrms,i = 200 m/s at an initial temperature T1 = 27°C = 300 K, we want to find the r.m.s. velocity at the new temperature T2 = 127°C = 400 K.
Using the relation:
vrms,2vrms,i = √ T2T1
Substitute the given values:
vrms,2200 = √ 400300 = √ 43
Thus:
vrms,2 = 200 × √ 43 = 200 × 2√3 = 400√3 m/s
Q2: A given sample of an ideal gas occupies a volume V at a pressure P and absolute temperature T. The mass of each molecule of the gas is m. Which of the following gives the density of the gas ? [2016]
(a) P/(kT)
(b) Pm/(kT)
(c) P/(kTV)
(d) mkT
Ans: (b) Pm/(kT)
Explanation:
We know that ideal gas equation is
PV = NkT
Where, P is the pressure
V is the volume
N is the number of molecules
k is the Boltzmann constant
T is the temperatureNow, the mass of the gas sample is given by:
M = N × m
Where m is the mass of one molecule.
The density (ρ) of the gas is:
ρ = MV = N × mV
From the ideal gas law PV = NkT, we can solve for NV (the number density):
NV = PkT
Substituting this into the density equation:
ρ = m × PkT
Thus, the density of the gas is:
ρ = PmkT
2015
Q1: The ratio of the specific heats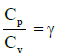 in terms of degrees of freedom (n) is given by: [2015]
in terms of degrees of freedom (n) is given by: [2015](a)
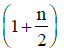
(b)
(c)
(d)
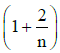
Ans: (d)
Explanation:
The ratio of the specific heats γ = CPCV is related to the degrees of freedom (n) of the gas molecules.
For a gas:
- CV(specific heat at constant volume) is given by:
CV = n2 R
- CP (specific heat at constant pressure) is related to CVas:
CP = CV + R = n2 R + R = (n + 2)2 R
Now, the ratio:
γ = CPCV = (n + 2)2 Rn2 R = n + 2n
Thus, the correct expression for γ is:
γ = 1 + 2n
Q2: Two vessels separately contain two ideal gases A and B at the same temperature, the pressure of A being twice that of B. Under such conditions, the density of A is found to be 1.5 times the density of B. The ratio of molecular weight of A and B is [2015]
(a) 2
(b) 1/2
(c) 2/3
(d) 3/4
Ans: (d) 3/4
Explanation:
According to an ideal gas equation, the molecular weight of an ideal gas is
M = ρRT / PAs:
P = ρRTM
where P, T, and ρ are the pressure, temperature, and density of the gas respectively, and R is the universal gas constant.
∴ The molecular weight of A is:
MA = ρARTAPA
and that of B is:
MB = ρBRTBPB
Hence, their corresponding ratio is:
MAMB = ρAρB × TATB × PBPA1
Here:
- ρA/ρB = 1.5 = 32
- TA/TB = 1
- PA/PB = 2
∴ MAMB = 32 × 1 × 12 = 34
2014
Q1: The mean free path of molecules of a gas,(radius ‘r’) is inversely proportional to: [2014]
(a) r
(b) √r
(c) r3
(d) r2
Ans: (d) r2
Explanation:
The mean free path (λ) of a gas molecule is the average distance a molecule travels between collisions. It is given by the formula:λ = 1√2 nπd2
Where:
- n is the number density (number of molecules per unit volume).
- d is the diameter of the gas molecule.
Since the diameter d is directly proportional to the radius r of the molecule (d = 2r), the mean free path is inversely proportional to the square of the radius (r2).
Thus, the mean free path is inversely proportional to r2.
|
96 videos|367 docs|98 tests
|
FAQs on NEET Previous Year Questions (2014-2025): Kinetic Theory - Physics Class 11
| 1. What is the Kinetic Theory of Gases? |  |
| 2. How does temperature affect the kinetic energy of gas molecules? |  |
| 3. What is the relationship between pressure and volume in gases according to the Kinetic Theory? |  |
| 4. Can the Kinetic Theory explain the behavior of real gases? |  |
| 5. How are effusion and diffusion explained by the Kinetic Theory? |  |