NEET Previous Year Questions (2014-2025): Oscillations | Physics Class 11 PDF Download
2025
Q1: In an oscillating spring mass system, a spring is connected to a box filled with the sand. As the box oscillates, sand leaks slowly out of the box vertically so that the average frequency ω (t) and average amplitude A (t) of the system changes with time t. Which of the following options systemically depicts these changes correctly? [2025]
(a) 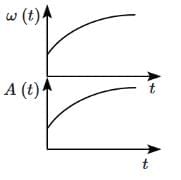
(b) 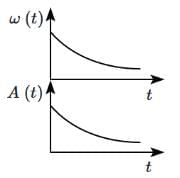
(c) 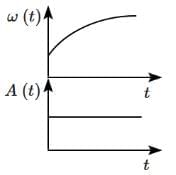
(d) 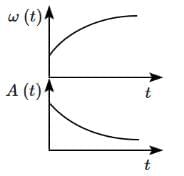
Ans: (d)
At any point of time, time period is given by
T = 2π √(m / k)
Here m is decreasing, so time period T will be decreasing
Since ω = 2π / T
Hence as mass leaks, ω will increase
Now, at any instant
mg = kx0
So, equilibrium length x0 = mg / k, where m is decreasing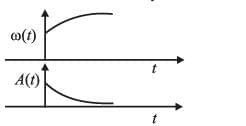
So, equilibrium length will decrease.
So, amplitude also go on decreasing.
Q2: Two identical point masses P and Q, suspended from two separate massless springs of spring constant k1 and k2, respectively, oscillate vertically. If their maximum speeds are the same, the ratio (AQ/AP) of the amplitude AQ of mass Q to the amplitude AP of mass P is: [2025]
(a) 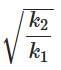
(b) 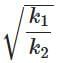
(c) 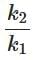
(d) 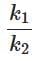
Ans: (b)
Maximum speed in simple harmonic motion is given by:
vmax = A × ω
Since the masses are identical, angular frequency ω is given by:
ω = √(k / m)
Let AP and AQ be amplitudes and ω1 and ω2 be angular frequencies of P and Q respectively.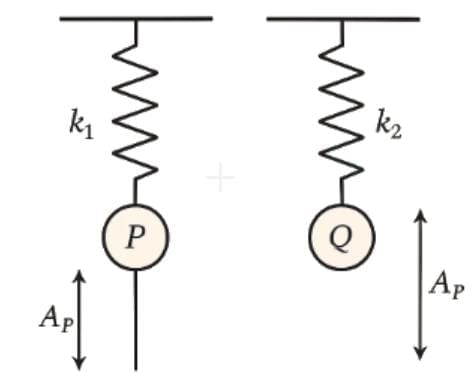
Given: vmax(P) = vmax(Q)
⇒ AP × ω1 = AQ × ω2
⇒ AQ / AP = ω1 / ω2
⇒ AQ / AP = √(k1) / √(k2)
⇒ AQ / AP = √(k1 / k2)
Therefore, the correct answer is Option B: √(k1 / k2)
2024
Q1: If the mass of the bob in a simple pendulum is increased to thrice its original mass and its length is made half its original length, then the new time period of oscillation is x / 2 times its original time period. Then the value of x is: [2024]
(a) √3
(b) √2
(c) √2
(d) 4
Ans: (b)
The period of oscillation, T, of a simple pendulum is determined by the formula: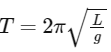
where:
- L is the length of the pendulum
- g is the acceleration due to gravity
The mass of the bob does not factor into the equation for the period.
Let's first denote the original length of the pendulum as L and the original period of oscillation as T1. Hence,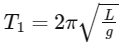
When the length of the pendulum is halved, the new length L' would be L / 2. Thus, the new period T2 can be calculated as:
We are given that the new period T2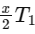 . Therefore, we can set up the equation:
. Therefore, we can set up the equation: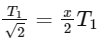
To find the value of x, we solve for x: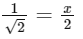
Multiplying both sides by 2: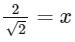
Simplify to:
Hence, the correct answer is:
Option B:
(a) 5 cm, 2 s
(b) 5 m, 2 s
(c) 5 cm, 1 s
(d) 5 m, 1 s
Ans: (b)
In the equation for simple harmonic motion (SHM), 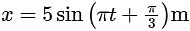 , the general form
, the general form 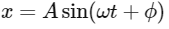 can be used to identify the parameters of SHM, where:
can be used to identify the parameters of SHM, where:
- A is the amplitude.
- ω (omega) is the angular frequency.
- φ (phi) is the phase constant.
- t is the time.
Comparing the given equation with the standard form:
- The amplitude A is 5 m, as that is the coefficient of sine in the equation.
- The angular frequency ω isπ rad/s.
The angular frequency ω is related to the time period T of the motion through the formula: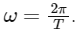
Given that ω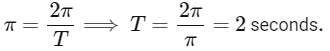
Hence, the amplitude of the motion is 5 m and the time period is 2 s. Thus, the correct answer is:
Option B: 5 m, 2 s
2023
Q1: The x-t graph of a particle performing simple harmonic motion is shown in the figure. The acceleration of the particle at t = 2 s is [2023]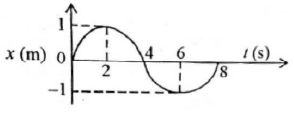 (a)
(a) 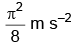
(b) 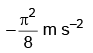
(c) 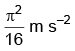
(d) 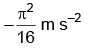
Ans: (d)
Solution: Position of particle as function of time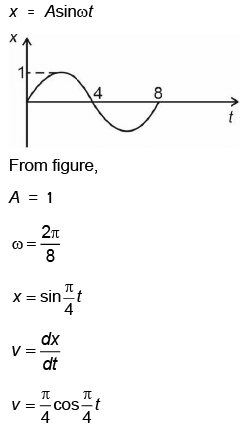
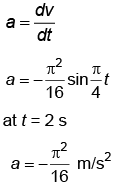
2022
Q1: Match List-I with List-II [2022]
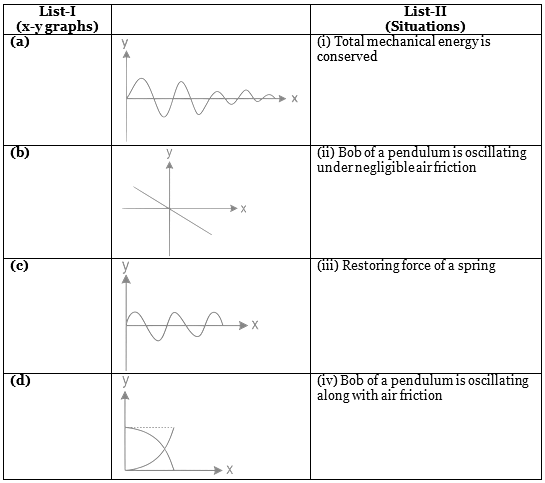
Choose the correct answer from the options given below
(a) (a) - (iii), (b) - (ii), (c) - (i), (d) - (iv)
(b) (a) - (iv), (b) - (ii), (c) - (iii), (d) - (i)
(c) (a) - (iv), (b) - (iii), (c) - (ii), (d) - (i)
(d) (a) - (i), (b) - (iv), (c) - (iii), (d) - (ii)
Ans: (c)
(a) Amplitude of oscillation is continuously decreasing. It means bob of pendulum oscillate with air friction.
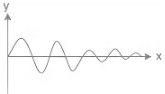
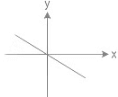
(b) F = -kx (restoring force of a spring)
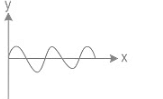
(c) Amplitude of oscillation is remains same. It means bob of pendulum is oscillating under negligible air resistance.
(d) 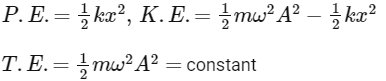
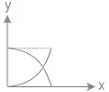
Q2: Identify the function which represents a non-periodic motion. [2022]
(a) 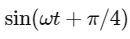
(b) e-ωt
(c) sinωt
(d) sinωt + cosωt
Ans: (b)
Here, 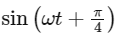
And 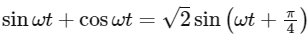
While,
Q3: Two pendulums of length 121 cm and 100 cm start vibrating in phase. At some instant, the two are at their mean position in the same phase. The minimum number of vibrations of the shorter pendulum after which the two are again in phase at the mean position is: [2022]
(a) 9
(b) 10
(c) 8
(d) 11
Ans: (d)
Solution:

2021
Q1: A body is executing simple harmonic motion with frequency 'n', the frequency of its potential energy is: [2021]
(a) 3n
(b) 4n
(c) n
(d) 2n
Ans: (d)
Solution: Displacement equation of SHM of frequency 'n' x = Asin(ωt) = Asin(2πnt) Now,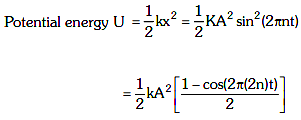
So frequency of potential energy = 2n
Q2: A spring is stretched by 5 cm by a force 10 N. The time period of the oscillations when a mass of 2 kg is suspended by it is: [2021]
(a) 3.14 s
(b) 0.628 s
(c) 0.0628 s
(d) 6.28 s
Ans:
Solution:
F = kx
10 = k(5 × 10–2)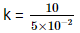
= 2 x 102
= 200 N/m
Now,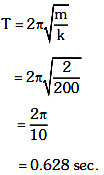
2020
Q1: The phase difference between displacement and acceleration of a particle in a simple harmonic motion is :
(a) 3π/2 rad
(b) π/2 rad
(c) Zero
(d) π rad [2020]
Ans: (d)
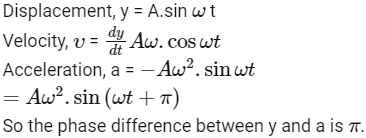
2019
Q1: Average velocity of a particle executing SHM in one complete vibration is: [2019]
(a) Aω/2
(b) Aω
(c) 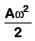
(d) Zero
Ans: (d)
Solution:
In one complete vibration, displacement is zero. So, average velocity in one complete vibration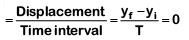
Q2: The displacement of a particle executing simple harmonic motion is given by y = A0+ Asinωt + Bcosωt
Then the amplitude of its oscillation is given by : [2019]
(a) 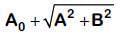
(b) 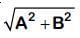
(c)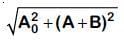
(d) A + B
Ans: (b)
Solution: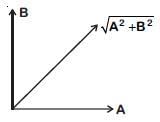
y = A0+ Asinωt + Bsinωt
Equate SHM
y' = y – A0 = Asinωt + Bcosωt
Resultant amplitude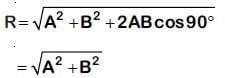
Q3: The radius of circle, the period of revolution, initial position and sense of revolution are indicated in the fig.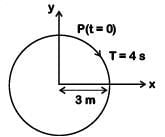
y - projection of the radius vector of rotating particle P is: [2019]
(a) y(t) = –3 cos2πt, where y in m
(b) 
(c) 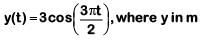
(d) 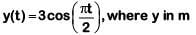
Ans: (d)
Solution:
At t = 0, y displacement is maximum, so equation will be cosine function.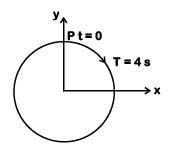
T = 4s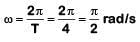
y = a cosωt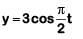
2018
Q1: A pendulum is hung from the roof of a sufficiently high building and is moving freely to and fro like a simple harmonic oscillator. The acceleration of the bob of the pendulum is 20 m/s2 at a distance of 5 m from the mean position. The time period of oscillation is:- [2018]
(a) 2πs
(b) πs
(c) 2s
(d) 1s
Ans: (b)
Solution: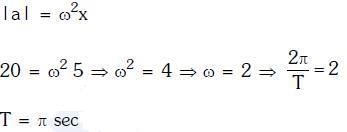
2017
Q1: A particle executes linear simple harmonic motion with an amplitude of 3 cm. When the particle is at 2 cm from the mean position, the magnitude of its velocity is equal to that of its acceleration. Then its time period in seconds is:- [2017]
(a) 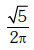
(b) 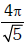
(c) 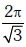
(d) 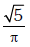
Ans: (b)
Solution:
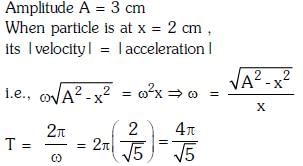
Q2: A spring of force constant k is cut into lengths of ratio 1 : 2 : 3. They are connected in series and the new force constant is K'. Then they are connected in parallel and force constant is k''. Then k' : k'' is [2017]
(a) 1 : 9
(b) 1 : 11
(c) 1 : 14
(d) 1 : 6
Ans: (b)
Let us assume, the length of spring be l.
When we cut the spring into ratio of length 1 : 2 : 3, we get three springs of lengths 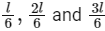 with force constant,
with force constant,
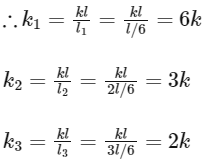
When connected in series,
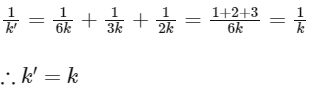
When connected in parallel,
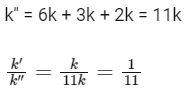
2016
(a) 3/4
(b) 4/3
(c) 16/9
(d) 9/16
Ans: (d)
The time period of oscillation is given by
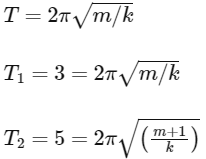
On dividing :
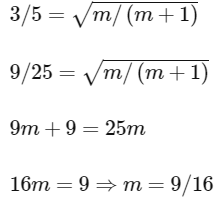
2015
Q1: A particle is executing SHM along a straight line. Its velocities at distances x1 and x2 from the mean position are V1 and V2, respectively. Its time period is: [NEET /AIPMT Cancelled Paper 2015]
(a) 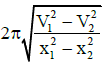
(b) 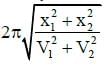
(c) 
(d) 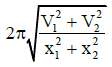
Ans: (c)
Solution:
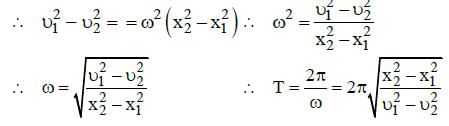
Q2: When two displacements represented by y1 = a sin(ωt) and y2 = b cos(ωt) are superimposed the motion is: [NEET /AIPMT Cancelled Paper 2015]
(a) simple harmonic with amplitude (a+b)/2
(b) not a simple harmonic
(c) simple harmonic with amplitude a/b
(d) simple harmonic with amplitude 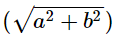
Ans: (d)
Solution: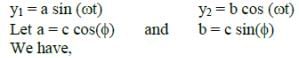
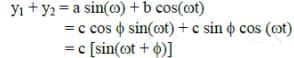
where c2 = a2 + b2 [since a2 + b2 = c2 cos (φ) + c2 sin (φ) = c2 ]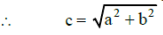
The superimposed motion is simple harmonic with amplitude 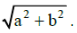
Q3: A particle is executing a simple harmonic motion. Its maximum acceleration is α and maximum velocity is β. Them, its time period of vibration will be [NEET / AIPMT 2015]
(a) β2/ α
(b) 2πβ / α
(c) β2/ α2
(d) α / β
Ans: (b)
As, we know, in SHM
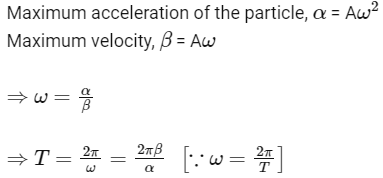
2014
Q1: The oscillation of a body on a smooth horizontal surface is represented by the equation,
X = A cos (ωt)
Where X = displacement at time t
ω = frequency of oscillation
Which one of the following graphs shows correctly the variation ‘a’ with ‘t’? [2014]
(a) 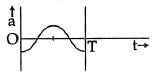
(b) 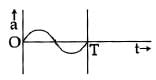
(c) 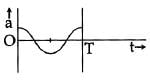
(d) 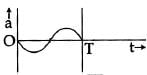
Here, a = acceleration at time ‘t’ and T = time period
Ans: (a)
Solution: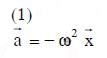
|
96 videos|367 docs|98 tests
|
FAQs on NEET Previous Year Questions (2014-2025): Oscillations - Physics Class 11
| 1. What is the formula for the time period of an oscillating spring-mass system? |  |
| 2. How does the amplitude of oscillation affect the energy of a system? |  |
| 3. What is the relationship between the frequency and the time period of an oscillating system? |  |
| 4. How does damping affect the motion of an oscillating system? |  |
| 5. What is the difference between free oscillations and forced oscillations? |  |






















