JEE Main Previous Year Questions (2016- 2024): Heat & Thermodynamics- 1 | Physics for Airmen Group X - Airforce X Y / Indian Navy SSR PDF Download
Q.1. Two moles of an ideal gas with CP/CV = 5/3 are mixed with 3 moles of another ideal gas with CP/CV = 4/3. The value of CP/CV for the mixture is (2020)
(1) 1.45
(2) 1.50
(3) 1.47
(4) 1.42
Ans. (4)
Solution.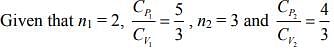
We know that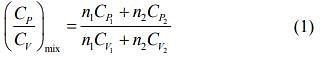
And CP - CV = nR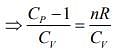
Rearranging the Eq.(1), we get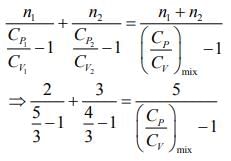
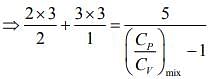
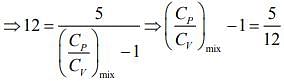
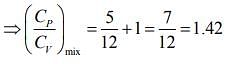
Q.2. Under an adiabatic process, the volume of an ideal gas gets doubled. Consequently, the mean collision time between the gas molecules changes from τ1 to τ2. If Cp/CV = γ for this gas, then a good estimate for τ2/τ1 is given by:
(1) 2
(2) 1/2
(3) (1/2)γ
(4) (1/2)γ+1/2
Ans. None
Solution.
We know that, adiabatic process is given by
TVγ-1 = constant
and relaxation time is given by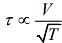
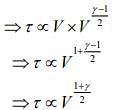
Given that, volume gets doubled under adiabatic process.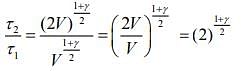
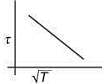
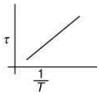
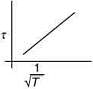
Q.3. The plot that depicts the behavior of the mean free time τ (time between two successive collisions) for the molecules of an ideal gas, as function of temperature (T), qualitatively, is (Graphs are schematic and not drawn to scale)
(1) 
(2)
(3) 
(4) 
Ans. (3)
Solution.
We know that
Mean free (λ) = Mean free time(τ) × Average speed (Vavg)
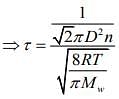
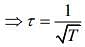
So, plot of option (3) depict the correct relation between mean free time and temperature.
Q.4. Consider a mixture of n moles of helium gas and 2n moles of oxygen gas (molecules taken to be rigid) as an ideal gas. Its CP/CV value will be:
(1) 19/13
(2) 67/45
(3) 40/27
(4) 23/15
Ans. (1)
Solution.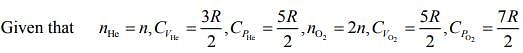
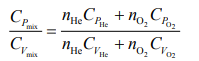
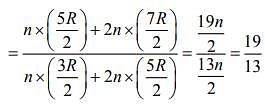
Q.5. Consider two ideal diatomic gases A and B at some temperature T. Molecules of the gas A are rigid, and have a mass m. Molecules of the gas B have an additional vibrational mode, and have a mass m/4. The ratio of the specific heats of gas A and B, respectively is
of gas A and B, respectively is
(1) 7 : 9
(2) 5 : 9
(3) 3 : 5
(4) 5 : 7
Ans. (4)
Solution.
Degree of freedom of a diatomic molecule if vibration is absent = 5
Degree of freedom of a diatomic molecule if vibration is present = 7
So, specific heat of gas A is given by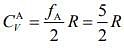 ....(1)
....(1)
So, specific heat of gas B is given by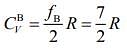 .....(2)
.....(2)
From Eqs. (1) and (2), we get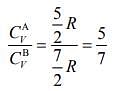
Q.6. Two gases – argon (atomic radius 0.07 nm, atomic weight 40) and xenon (atomic radius 0.1 nm, atomic weight 140) have the same number density and are at the same temperature. The rate of their respective mean free times is closest to
(1) 3.67
(2) 1.83
(3) 2.3
(4) 4.67
Ans. None
Solution.
Given that MAg = 40,rAg = 0.07 nm, MXe = 140,rXe = 0.1nm
Mean free time of a gas molecules is given by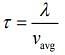
Mean free path of a gas molecules is given by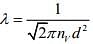
Average velocity of a gas molecule is given by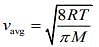
So,
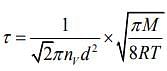

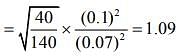
Q.7. A litre of dry air at STP expands adiabatically to a volume of 3 L. If γ = 1.40, the work done by air is (31.4 = 4.6555) [Take air to be an ideal gas]
(1) 60.7 J
(2) 90.5 J
(3) 100.8 J
(4) 48 J
Ans. (2)
Solution.
Given that V1 = 1L, V2 = 3L, P1 = 1 atm, γ = 1.40
For adiabatic process, we know that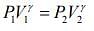 ....(1)
....(1)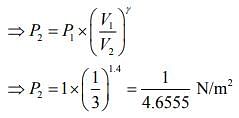
and work done is given by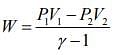 ....(2)
....(2)
Q.8. A Carnot engine operates between two reservoirs of temperatures 900 K and 300 K. The engine performs 1200 J of work per cycle. The heat energy (in J) delivered by the engine to the low temperature reservoir, in a cycle, is ____.
Ans. 600
Solution.
Given that T1 = 900 K, T2 = 300 K and W = 1200J
We know that for Carnot’s engine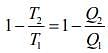
Where T1 is temperature of source, T2 is temperature of sink, Q1 is heat extracted from source and Q2 is heat released to sink.
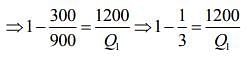
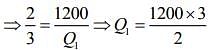
⇒ Q1 = 1800 J
We have W = Q1 – Q2 = 1200 J
⇒ Q2 = Q1 - 1200 J = 1800 J - 1200 J
⇒ Q2 = 600 J
So heat energy delivered by engine to the low temperature reservoir (sink) is 600 J.
Q.9. Two ideal Carnot engines operate in cascade (all heat given up by one engine is used by the other engine to produce work) between temperatures, T1 and T2. The temperature of the hot reservoir of the first engine is T1 and the temperature of the cold reservoir of the second engine is T2. T is temperature of the sink of first engine which is also the source for the second engine. How is T related to T1 and T2, if both the engines perform equal amount of work?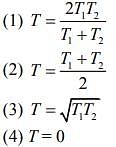
Ans. (2)
Solution.
Given that, two ideal Carnot engines in cascade between temperatures T1 and T2
Where T1 is temperature of hot reservoir of first engine, T2 is temperature of cold reservoir of second engine and T is temperature of sink of first engine and source of second engine.
We know,
work done by first engine = work done by second engine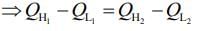
Here, 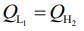
So, 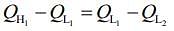
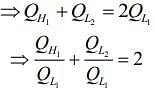
We have 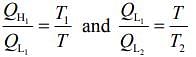
Then 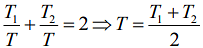
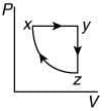
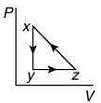
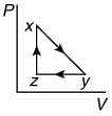
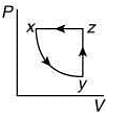
Q.10. A thermodynamic cycle xyzx is shown on a V-T diagram.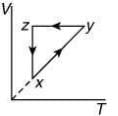
The P-V diagram that best describes this cycle is (Diagrams are schematic and not to scale)
(1) 
(2) 
(3) 
(4) 
Ans. (1)
Solution.
the V-T graph shows three process in cycle xyzx.
xy shows isobaric process
yz shows isochoric process
zx shows isothermal process
The correct P-V graph shows these three processes in cycle xyzx is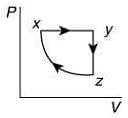
Q.11. A Carnot engine having an efficiency of 1/10 is being used as a refrigerator. If the work done on the refrigerator is 10 J, the amount of heat absorbed from the reservoir at lower temperature is
(1) 99 J
(2) 100 J
(3) 1 J
(4) 90 J
Ans. (4)
Solution.
Given that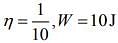
Work done by the Carnot engine as a refrigerator is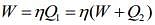
Where Q1 is heat given by the source and Q2 is heat absorbed by the reservoir.
So, 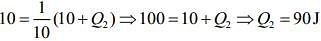
Q.12. Which of the following is an equivalent cyclic process corresponding to the thermodynamic cycle given in the figure? Where, 1 → 2 is adiabatic.
(Graphs are schematic and are not to scale)
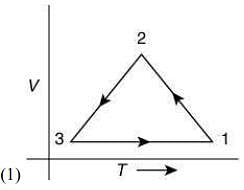
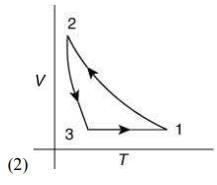
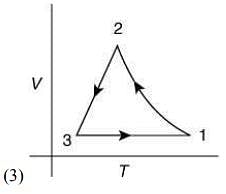
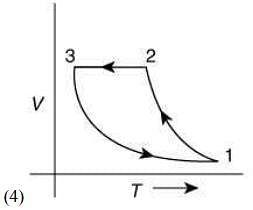
Ans. (3)
Solution.
Given graph shows that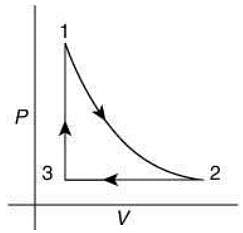
Path 1 → 2 is adiabatic process (Heat is constant)
Path 2 → 3 is isobaric process (Pressure is constant)
Path 3 → 1 is isochoric process (Volume is constant)
Only graphs in option (1) and (3) shows path 2 → 3 is isobaric process and path 3 → 1 is isochoric process.
But only graph in option (3) shows path 1 → 2 is adiabatic process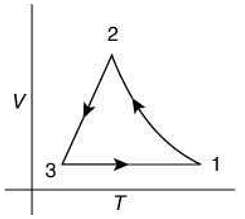
Q.13. Starting at temperature 300 K, one mole of an ideal diatomic gas (γ = 1.4) is first compressed adiabatically from volume V1 to V2 = V1/16. It is then allowed to expand isobarically to volume 2V2. If all the processes are the quasi-static then the final temperature of the gas (in °K) is (to the nearest integer) _________.
Ans. 1819
Solution.
Given that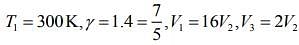
For first thermodynamic process, that is, adiabatically compression, we have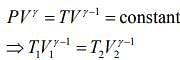
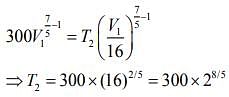
For second thermodynamic process, that is, Isobaric expansion, we have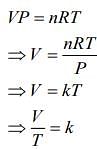
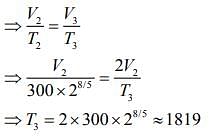
Q.14. A non-isotropic solid metal cube has coefficients of linear expansion as 5 × 10-5 /ºC along the x-axis and 6 × 10-6 /ºC along the y and z-axis. If the coefficient of volume expansion of the solid is C × 10-6 /ºC then the value of C is _______.
Ans. 60
Solution.
Given that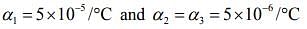
The coefficient of volume expansion of solid is given by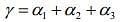
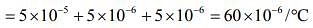
Therefore, C = 60
Q.15. M grams of steam at 100°C is mixed with 200 g of ice at its melting point in a thermally insulated container. If it produces liquid water at 40°C [heat of vaporization of water is 540 cal/g and heat of fusion of ice is 80 cal/g], the value of M(in gm.) is _________.
Ans. 40
Given that, steam is mixed with ice to produce to water
mass of steam = M
mass of ice Mi = 200 g
Temperature of steam, Ts = 100°C
Temperature of water, Tw = 40°C
Heat of vaporization, Lv = 540 cal/g
Heat of fusion, Lf = 80 cal/g
We know that,
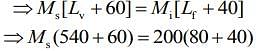
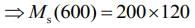
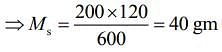
Q.16. A leak proof cylinder of length 1 m, made of a metal which has very low coefficient of expansion is floating vertically in water at 0°C such that its height above the water surface is 20 cm. When the temperature of water is increased to 4°C, the height of the cylinder above the water surface becomes 21 cm. The density of water at T = 4°C, relative to the density at T = 0°C is close to
(1) 1.26
(2) 1.04
(3) 1.01
(4) 1.03
Ans. (3)
Solution.
Given that
L = 1 m, l0 = 20 cm, l4 = 21 cm
We know that mass of merge body is equal to mass of the liquid. So,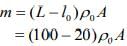
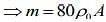 ....(1)
....(1)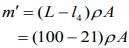
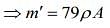 ...(2)
...(2)
Since, mass of the merge body is same in both cases. So,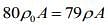
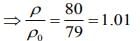
Q.17. Three containers C1, C2 and C3 have water at different temperatures. The table below shows the final temperature T when different amounts of water (given in liters) are taken from each container and mixed (assume no loss of heat during the process)
The value of θ (in ºC to the nearest integer) is ____.
Ans. 50
Solution.
Let temperatures of the three containers be T1, T2, T3.
From law of calorimetry in mixture (when mixing same liquid of different temperatures), we know that 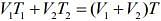
So, given table can be written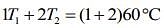
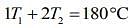 ....(1)
....(1)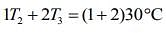
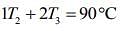 ....(2)
....(2)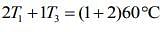
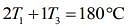 ....(3)
....(3)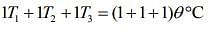
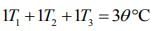 ....(4)
....(4)
Add Eqs (1), (2) and (3), we get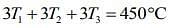
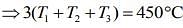
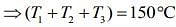 ....(5)
....(5)
From Eqs. (4) and (5), we get
Q.18. Temperature difference of 120°C is maintained between two ends of a uniform rod AB of length 2L. Another bent rod PQ, of same cross-sections as AB and length 3L / 2, is connected across AB (see figure). In steady-state, temperature difference between P and Q will be close to (2019)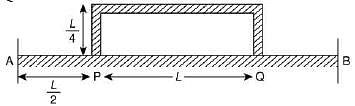
(1) 45°C
(2) 75°C
(3) 60°C
(4) 35°C
Ans. (1)
Solution.
Suppose the thermal conductivity is uniform for all rods.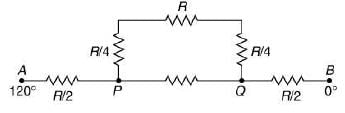
Now, total resistance = 8R/5
Thus,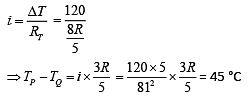
Q.19. An unknown metal of mass 192 g heated to a temperature of 100°C was immersed into a brass calorimeter of mass 128 g containing 240 g of water at a temperature of 8.4°C. Calculate the specific heat of the unknown metal if water temperature stabilizes at 21.5°C (specific heat of brass is 394 J kg−1 K−1). (2019)
(1) 458 J kg−1 K−1
(2) 1232 J kg−1 K−1
(3) 916 J kg−1 K−1
(4) 654 J kg−1 K−1
Ans. (3)
Solution.
Let s be the specific heat of unknown metal.
We have stabilized temperature is 21.5 °C
192 × s × (100 – 21.5) = 128 × 392 × (21.5 – 8.1) + 240 × 42
⇒ 15072 × s = 657305.6 – 132048 (21.5 – 8.4)
⇒ s = 916 J kg−1 K−1
Q 20. Ice at −20°C is added to 50 g of water at 40°C. When the temperature of the mixture reaches 0°C, it is found that 20 g of ice is still unmelted. The amount of ice added to the water was close to (specific heat of water = 4.2 J/g/°C; specific heat of ice = 2.1 J/g/°C; heat of fusion of water at 0°C = 334 J/g) (2019)
(1) 50 g
(2) 60 g
(3) 40 g
(4) 100 g
Ans. (3)
Solution.
Let amount of ice is m.
According to principal of calorimeter,
Heat taken by ice = Heat given by water
⇒ 20 × 2.1 × m + (m – 2) × 334 = 50 × 4.2 × 40
⇒ 376m – 6680 = 8400
⇒ 367m = 8400 + 6680
⇒ 367m = 15080
⇒ m = 41.08 ≈ 40 g
Q.21. A thermometer graduated according to a linear scale reads a value x0 when in contact with boiling water, and x0/3 when in contact with ice. What is the temperature of an object in °C, if this thermometer in the contact with the object reads x0/2? (2019)
(1) 25
(2) 60
(3) 40
(4) 35
Ans. (1)
Solution.
We have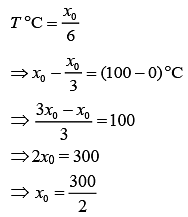
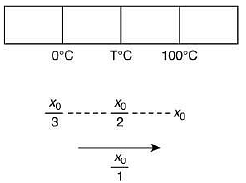
Therefore, 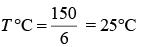
Q.22. A metal ball of mass 0.1 kg is heated up to 500°C and dropped into a vessel of heat capacity 800 J/K and containing 0.5 kg water. The initial temperature of water and vessel is 30°C. What is the approximate percentage increment in the temperature of the water? (Specific heat capacities of water and metal are, respectively, 4200 J kg−1 K−1 and 400 J kg−1 K−1) (2019)
(1) 15%
(2) 30%
(3) 25%
(4) 20%
Ans. (4)
Solution.
We have,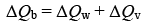
⇒ 0.1 × 400 × (500 – T) = 0.5 × 4200 (T – 30) + 800 (T – 30)
⇒ 40(500 – T) = (T – 30) (2100 + 800)
⇒ 20000 – 40T = 2900T – 30 × 2900
⇒ 2940T = 30 × 2900 + 20,000
⇒ 2940T = 1,07,000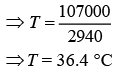
Therefore, percentage rise in temperature 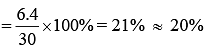
Q.23. Two rods A and B of identical dimensions are at temperature 30°C. If A is heated up to 180°C and B up to T°C, then the new lengths are the same. If the ratio of the coefficients of linear expansion of A and B is 4 : 3, then the value of T is (2019)
(1) 230°C
(2) 270°C
(3) 200°C
(4) 250°C
Ans. (1)
Solution.
Let Δl1 and Δl2 are change in length.
The length of both the rods are same.
Thus, Δl1 = Δl2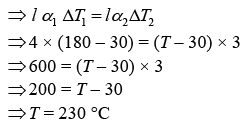
Q.24. When 100 g of a liquid A at 100°C is added to 50 g of a liquid B at temperature 75°C, the temperature of the mixture becomes 90°C. The temperature of the mixture, if 100 g of liquid A at 100°C is added to 50 g of liquid B at 50°C, will be (2019)
(1) 85°C
(2) 60°C
(3) 80°C
(4) 70°C
Ans. (3)
Solution.
Energy lost by liquid = Energy given by liquid
mass × specific heat × temperature = mass × specific heat × temperature
⇒ 100 × CA × [100 – 90] = 50 × CB × [90 – 75]
⇒ 100 × 10 × CA = 50 × CB × 15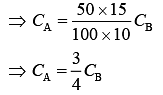
Now,
100 × CA × [100 – T] = 50 × CB × (T – 50)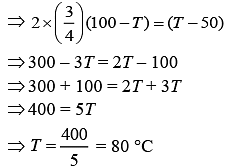
Q.25. A cylinder of radius R is surrounded by a cylindrical shell of inner radius R and outer radius 2 R . The thermal conductivity of the material of the inner cylinder is K1 and that of the outer cylinder is K2. Assuming no loss of heat, the effective thermal conductivity of the system for heat flowing along the length of the cylinder is (2019)
(1) 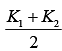
(2) K1 + K2
(3) 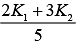
(4) 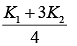
Ans. (4)
Solution.
Thermal Resistance,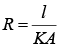 (K = thermal conductivity)
(K = thermal conductivity)
Thermal Resistance of inner cylinder of Radius R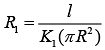 (1)
(1)
Thermal Resistance of outer cylinder of radius 2R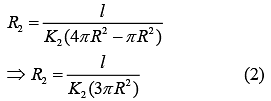
Now, equivalent thermal Resistance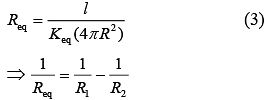
Q.26. A gas can be taken from A to B via two different processes ACB and ADB. When path ACB is used 60 J of heat flows into the system and 30 J of work is done by the system. If path ADB is used work done by the system is 10 J. The heat flow into the system in path ADB is (2019)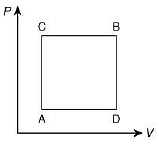
(1) 40 J
(2) 80 J
(3) 100 J
(4) 20 J
Ans. (1)
Solution.
Heat flow in path ACB, ΔQ = 60 J
Work done by system ACB, ΔW = 30 J
So,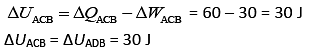
Now, work done by path ADB, ΔW = 10 J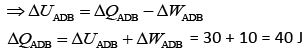
Q.27. Two Carnot engines A and B are operated in series. The first one, A, receives heat at T1 (= 600 K) and rejects to a reservoir at temperature T2. The second engine B receives heat rejected by the first engine and, in turn, rejects to a heat reservoir at T3 (= 400 K). Calculate the temperature T2 if the work outputs of the two engines are equal. (2019)
(1) 600 K
(2) 400 K
(3) 300 K
(4) 500 K
Ans. (4)
Solution.
Let E1 and E2 be the two engines.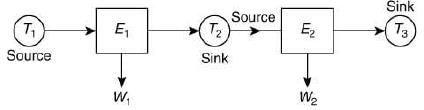
E1 engine absorb the T1 heat from source and exhausts it to sink at T2. Sink of Engine E1 is source for engine E2 at T2.
Let W1 and W2 be the work of Engine E1 and E2 Thus, W1 = W2
⇒ ΔV1 = ΔV2
⇒ T1 – T2 = T2 – T3
⇒ T1 + T3 = 2T2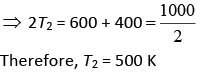
Q.28. A heat source at T = 103 K is connected to another heat reservoir at T = 102 K by a copper slab which is 1 m thick. Given that the thermal conductivity of copper is 0.1 WK−1 m−1, the energy flux through it in the steady state is (2019)
(1) 90 Wm−2
(2) 120 Wm−2
(3) 65 Wm−2
(4) 200 Wm−2
Ans. (1)
Solution.
Heat current is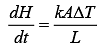
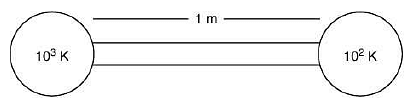
Heat flux is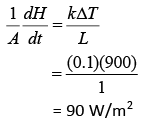
Q.29. Three Carnot engines operate in series between a heat source at a temperature T1 and a heat sink at temperature T4 (see figure). There are two other reservoirs at temperature T2 and T3, as shown, with T1 > T2 > T3 > T4. The three engines are equally efficient if (2019)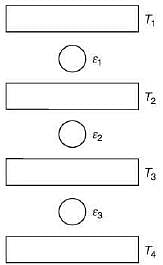
(1)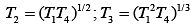
(2)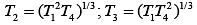
(3) 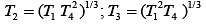
(4) 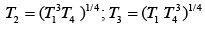
Ans. (2)
Solution.
Efficiency of Carnot engine is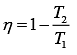
Let η1, η2 and η3 are efficiency of three Carnot engines.
Thus,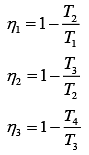
According to the question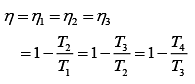
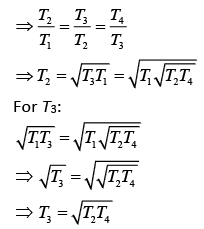
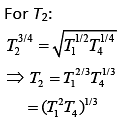
Q.30. Half mode of an ideal monoatomic gas is heated at constant pressure of 1 atm from 20°C to 90°C. Work done by gas is close to (gas constant R = 8.31 J/mol.K) (2019)
(1) 581 J
(2) 291 J
(3) 146 J
(4) 73 J
Ans. (2)
Solution.
We have,
R = 1 atm, n = 0.5
T1 = 20 °C, T2 = 90 °C
Therefore, work done = PΔV = nRΔT
= nR(T2 – T1)
= 0.5 × 8.31 × (90 – 20)
= 0.5 × 8.31 × 70 = 291 J
Q.31. A rigid diatomic ideal gas undergoes an adiabatic process at room temperature. The relation between temperature and volume for this process is TVx = constant, then x is (2019)
(1) 2/5
(2) 5/3
(3) 2/3
(4) 3/5
Ans. (1)
Solution.
For adiabatic process,
⇒ x = 2/5
Q.32. In a process, temperature and volume of one mole of an ideal monoatomic gas are varied according to the relation VT = K, where K is a constant. In this process, the temperature of the gas is increased by ∆T. The amount of heat absorbed by gas is (R is gas constant) (2019)
(1) 1/2RΔT
(2) 1/2KRΔT
(3) 3/2RΔT
(4) 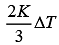
Ans. (1)
Solution.
We have,
VT = K (1)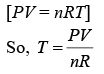
Put this value in Eq. (1), we get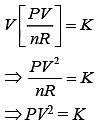
For polytropic process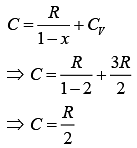
Therefore, amount of heat absorbed is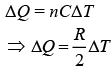
Q.33. For the given cyclic process CAB as shown for a gas, the work done is (2019)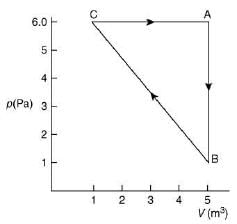
(1) 30 J
(2) 10 J
(3) 1 J
(4) 5 J
Ans. (2)
Solution.
Work done by a gas is area under cyclic diagram.
Therefore, work done by gas 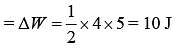
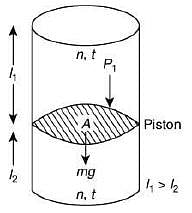
Q.34. A vertical closed cylinder is separated into two parts by a frictionless piston of mass m and of negligible thickness. The piston is free to move along the length of the cylinder. The length of the cylinder above the piston is l1, and that below the piston is l2, such that l1 > l2. Each part of the cylinder contains n moles of an ideal gas at equal temperature T. If the piston is stationary, its mass, m, will be given by (R is universal gas constant and g is the acceleration due to gravity) (2019)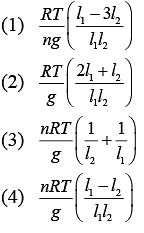
Ans. (4)
Solution.
Let A be the area of the piston.
Since, the cylinder exert more pressure (P2) on the lower part of the cylinder,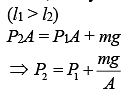
We know that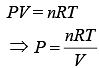
Thus,
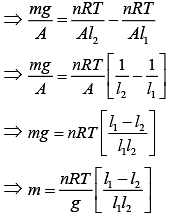
Q.35. A mixture of 2 moles of helium gas (atomic mass = 4u), and 1 mole of argon gas (atomic mass = 40 u) is kept at 300 K in a container. The ratio of their rms speeds 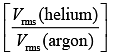 is close to (2019)
is close to (2019)
(1) 3.16
(2) 0.32
(3) 0.45
(4) 2.24
Ans: (1)
Solution:
rms velocity is given by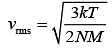 (1)
(1)
Since, both the gases are at same temperature,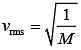
where M is molar mass of the gas.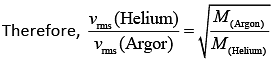
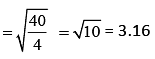
Q.36. A 15 g mass of nitrogen gas is enclosed in a vessel at a temperature 27°C. Amount of heat transferred to the gas, so that rms velocity of molecules is doubled, is about [take R = 83 J/K mole) (2019)
(1) 0.9 kJ
(2) 6 kJ
(3) 10 kJ
(4) 14 kJ
Ans. (3)
Solution.
Molar heat is given by Q = n CVΔT
Nitrogen is diatomic gas 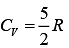
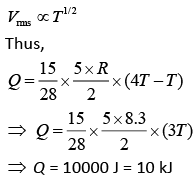
Q.37. Two kg of a monoatomic gas is at a pressure of 4 × 104 N/m2. The density of the gas is 8 kg/m3. What is the order of energy of the gas due to its thermal motion? (2019)
(1) 103 J
(2) 105 J
(3) 104 J
(4) 106 J
Ans. (3)
Solution.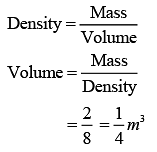
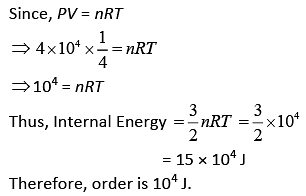
Q.38. A gas mixture consists of 3 moles of oxygen and 5 moles of argon at temperature T. Considering only translational and rotational modes, the total internal energy of the system is (2019)
(1) 15RT
(2) 20RT
(3) 4RT
(4) 12RT
Ans. (1)
Solution.
we have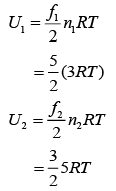
Therefore, total energy, U = U1 + U2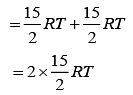
⇒ U = 15 RT
Q.39. An ideal gas occupies a volume of 2 m3 at a pressure of 3 × 106 Pa. The energy of the gas is (2019)
(1) 9 × 106 J
(2) 6 × 104J
(3) 108 J
(4) 3 × 102 J
Ans. (1)
Solution.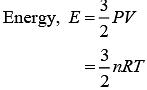
Where, R = Universal gas constant
T = Temperature of gas
Given, P = 3 × 106 Pa
V = 2 m3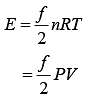
Let gas is monoatomic f = 3
therefore, 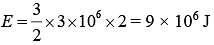
Q.40. An ideal gas is enclosed in a cylinder at pressure of 2 atm and temperature, 300 K. The mean time between two successive collisions is 6 × 10−8 s. If the pressure is doubled and temperature is increased to 500 K, the mean time between two successive collisions will be close to (2019)
(1) 2 × 10−7 s
(2) 4 × 10−8 s
(3) 0.5 × 10−8 s
(4) 3 × 10−6 s
Ans. (2)
Solution.
Mean free path of a gas molecule is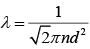 (1)
(1)
where n = number of molecules per unit volume
n = N/V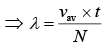 (2)
(2)
From Eq. (1) and Eq. (2), we get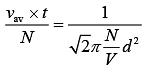
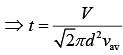 (3)
(3)
As we know that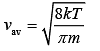
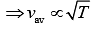 (4)
(4)
From Eq. (3) and Eq. (4), we get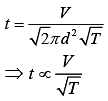
Equation of ideal gas is
PV = nRT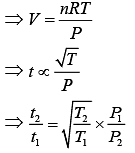
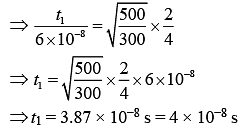
Q.41. Two moles of an ideal monoatomic gas occupies a volume V at 270C. The gas expands adiabatically to a volume 2 V. Calculate (a) the final temperature of the gas and (b) change in its internal energy. (2018)
(1) (a) 189 K (b) 2.7 kJ
(2) (a) 195 K (b) -2.7 kJ
(3) (a) 189 K (b) -2.7 kJ
(4) (a) 195 K (b) 2.7 kJ
Ans. (3)
Solution.
Initially n = 2, v, T= 300k
Finally Vd = 2v
Gas is monoatomic, So, r = 5/3
So,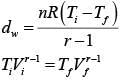
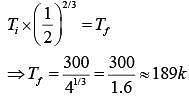
Since gas undergoes expensed.
Q.42. The mass of a hydrogen molecule is 3.32 x 10-27 kg. If 1023 hydrogen molecules strike, per second, a fixed wall of area 2 cm2 at an angle of 450 to the normal, and rebound elastically with a speed of 103 m/s, then the pressure on the wall is nearly: (2018)
(1) 2.35 x 103 N /m2
(2) 4.70 x 103 N /m2
(3) 2.35 x 102 N /m2
(4) 4.70 x 102 N /m2
Ans. (1)
Solution.
Change in momentum normal to the wall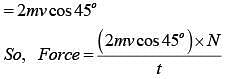
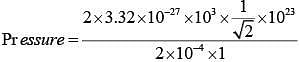
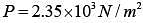
|
199 videos|422 docs|281 tests
|



















