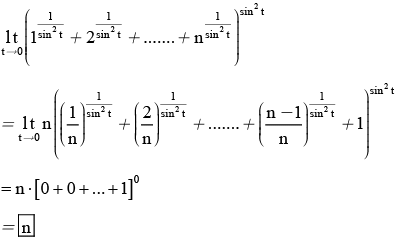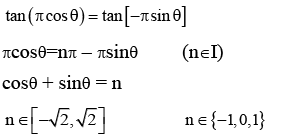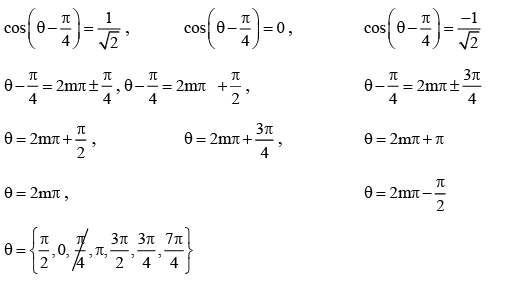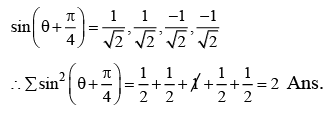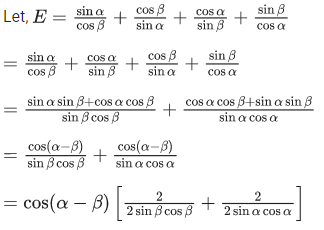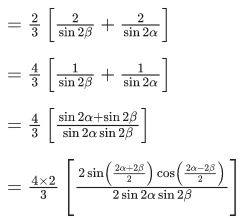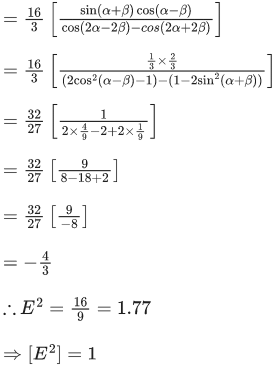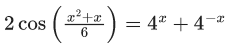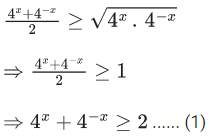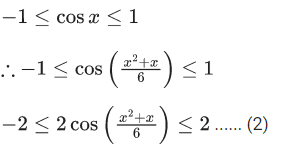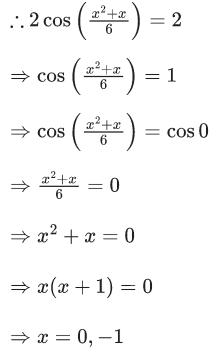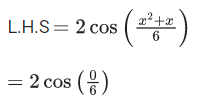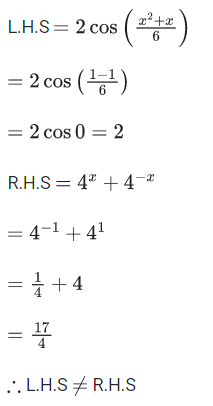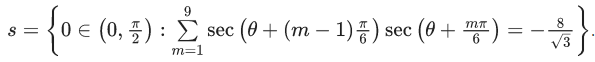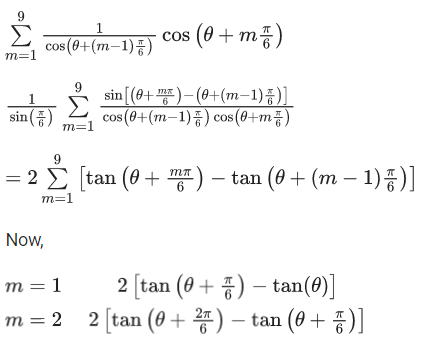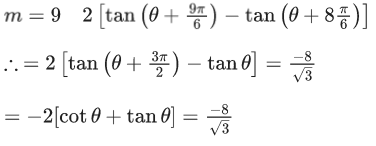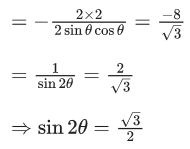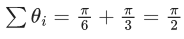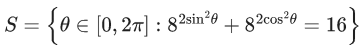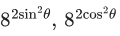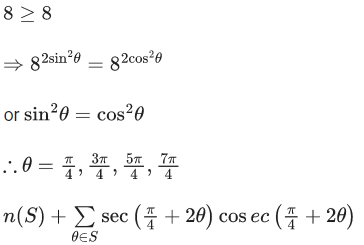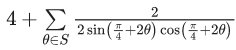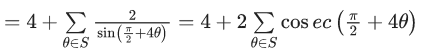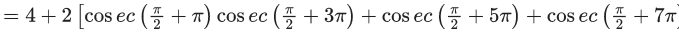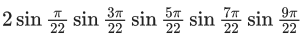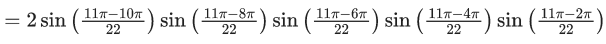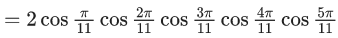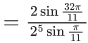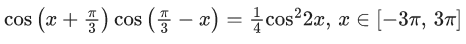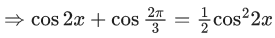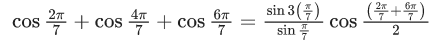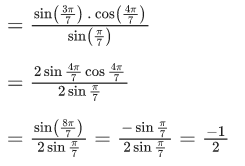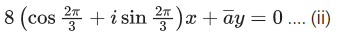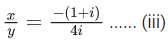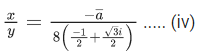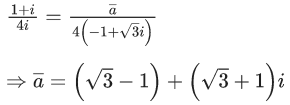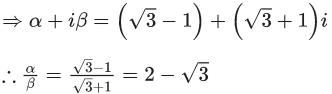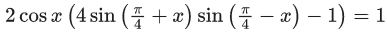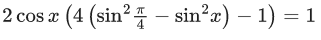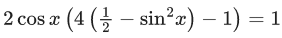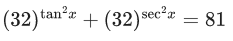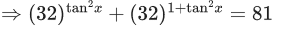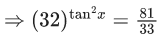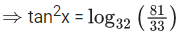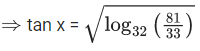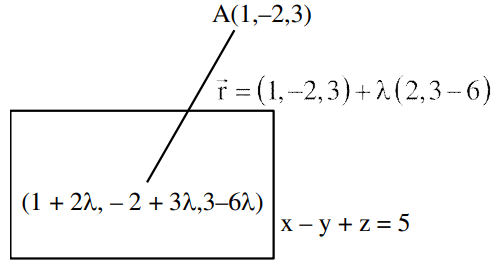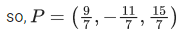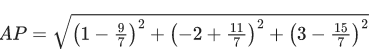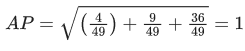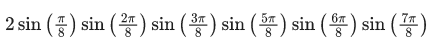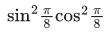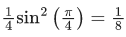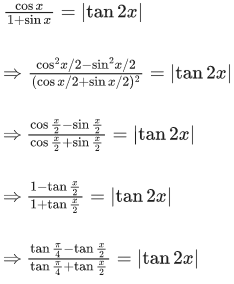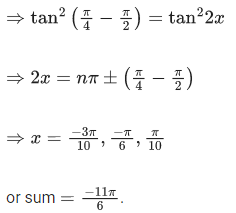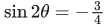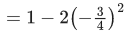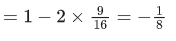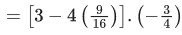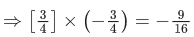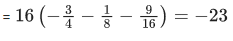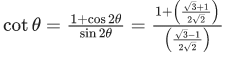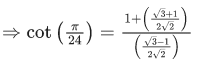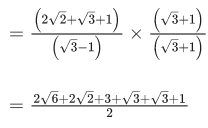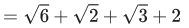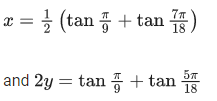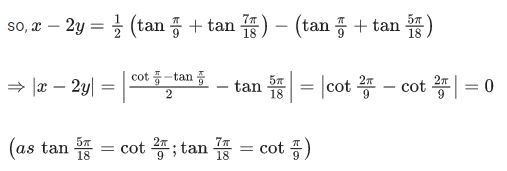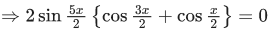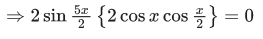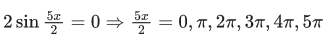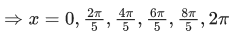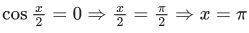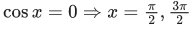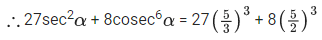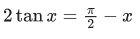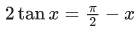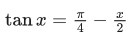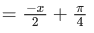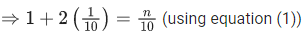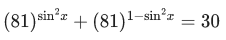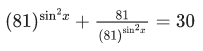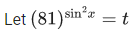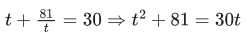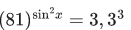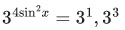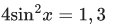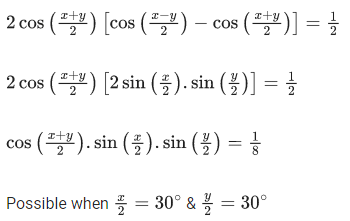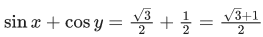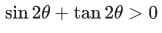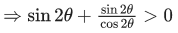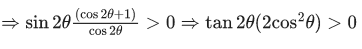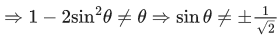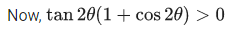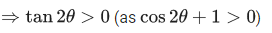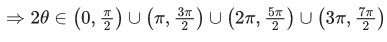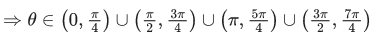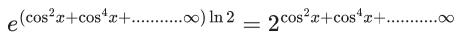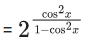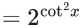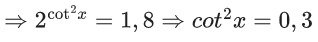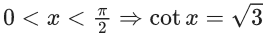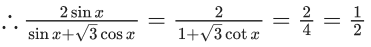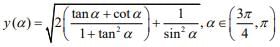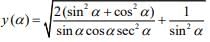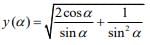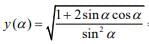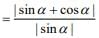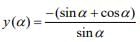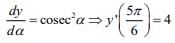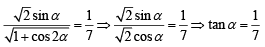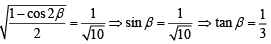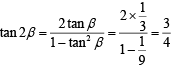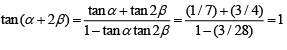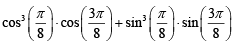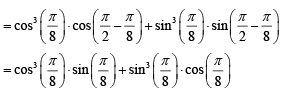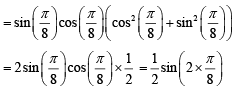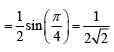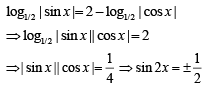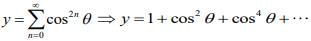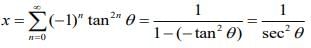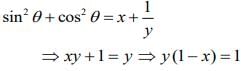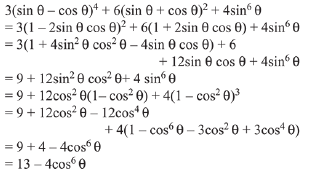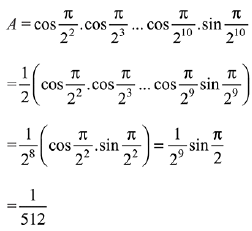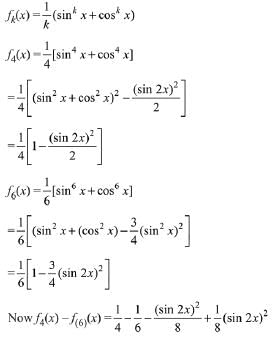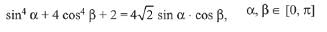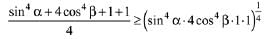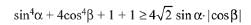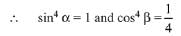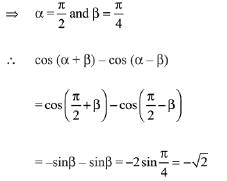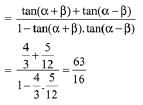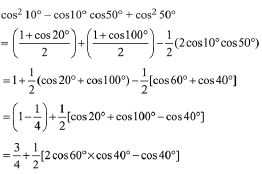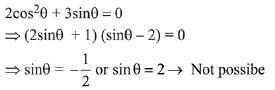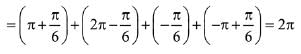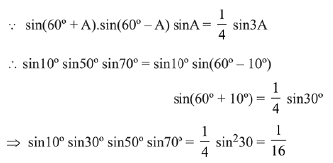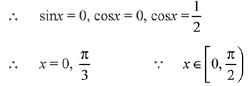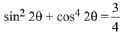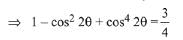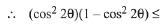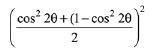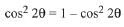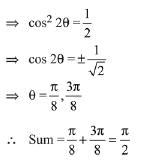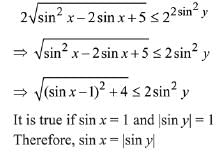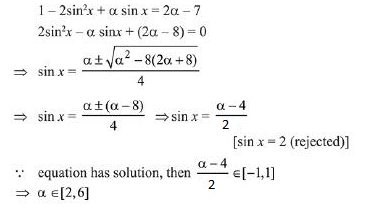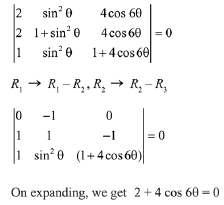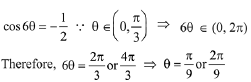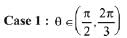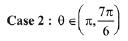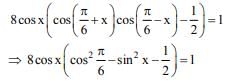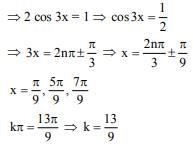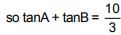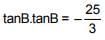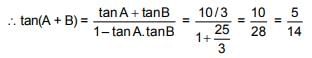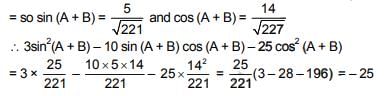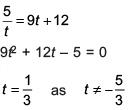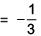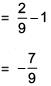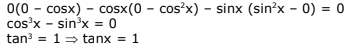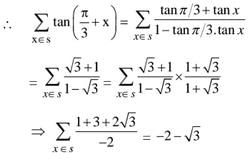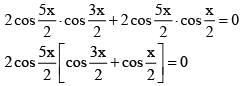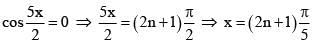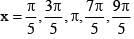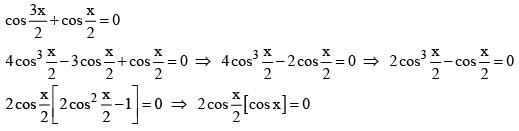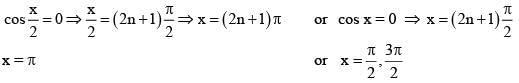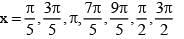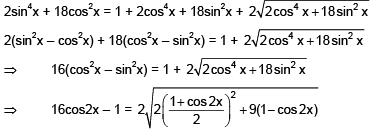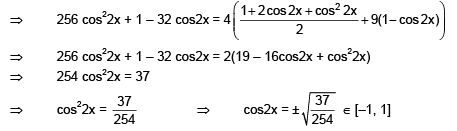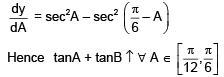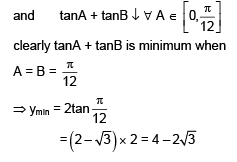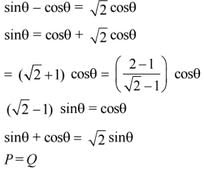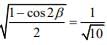JEE Main Previous Year Questions (2016- 2024): Trigonometric Functions & Equations | 35 Years Chapter wise Previous Year Solved Papers for JEE PDF Download

Q.1. 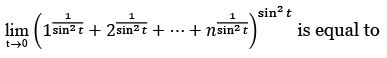                        (JEE Main 2023)
(a) n2
(b)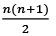
(c) n
(d) n² + n

Ans. c

Q.2. Let S = {θ ∈ [0,2π): tan⁡(πcos⁡θ) + tan⁡( πsin⁡θ) = 0}.                     (JEE Main 2023)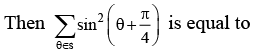

Ans. 2

Q.3. Let α and β be real numbers such that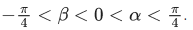
If sin⁡(α + β) = 13 and cos⁡(α − β) = 2/3, then the greatest integer less than or equal to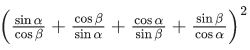
 is              (JEE Advanced 2022)

Ans. 1
Given, sin⁡(α + β) = 1/3
and cos⁡(α − β) = 2/3

Q.4. The number of elements in the set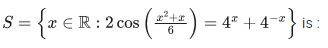
                     (JEE Main 2022)
(a) 1
(b) 3
(c) 0
(d) infinite

Ans. a
Given,

We know,
A.M ≥ G.M
∴ for 4x and 4^−x     

And we know,

(1) and (2) both satisfies only when both equal to 2.

When x = 0,

= 2 cos ⁡0
= 2.1
= 2
R.H.S = 4^x + 4^−x
= 4⁰ + 4⁰
= 2
∴ x = 0 is accepted.
Now, when x = −1,

∴ x = −1 is not a solution.
∴ Only one solution possible which is x = 0.

Q.5.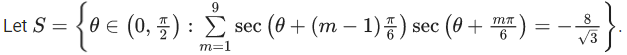
 
Then                            (JEE Main 2022)
(a)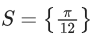
(b)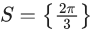
(c)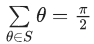
(d)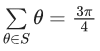

Ans. c




2θ = π/3
2θ = 2π/3
θ = π/6
θ = π/3

Q.6.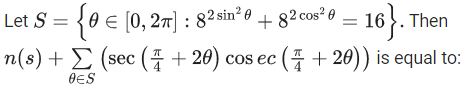
                  (JEE Main 2022)
(a) 0
(b) -2
(c) -4
(d) 12

Ans. c

Now apply AM ≥ GM for






= 4 - 2(4)
= 4 - 8
= -4

Q.7. 2 sin (π/22) sin (3π/22) sin (5π/22) sin (7π/22) sin (9π/22) is equal to :                    (JEE Main 2022)
(a) 3/16
(b) 1/16
(c) 1/32
(d) 9/32

Ans. b




= 1/16

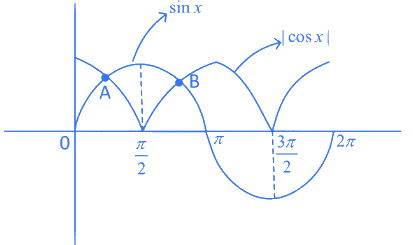
Q.8. The number of solutions of |cos⁡ x|= sin⁡ x, such that − 4π ≤ x ≤ 4π is :                    (JEE Main 2022)
(a) 4
(b) 6
(c) 8
(d) 12

Ans. c
Period of |cos⁡x| = π
And period of sin⁡x = 2π

Graph of sin x and |cos ⁡x| cuts each other at two points A and B in [0, 2π]
So, in [−4π, 4π], total 4 similar graph will be present and graph of sin ⁡x and |cos⁡ x| will cut 4 × 2 = 8 times.
∴ Total possible solutions = 8.

Q.9. Let S = {θ ∈ [-π, π] - {±  π/2}  : sinθ tanθ + tanθ = sin 2θ}
If 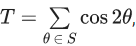 then T + n(S) is equal to:                    (JEE Main 2022)
(a) 7 + √3
(b) 9
(c) 8 +√3
(d) 10

Ans. b

Q.10. The number of solutions of the equation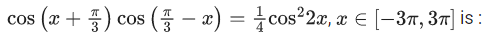
                    (JEE Main 2022)
(a) 8
(b) 5
(c) 6
(d) 7

Ans. d


⇒ cos²2x − 2cos⁡2x − 1 = 0
⇒ cos⁡ 2x = 1
∴ x = −3π, −2π, −π, 0, π, 2π, 3π
∴ Number of solutions = 7

Q.11. The value of 2sin (12^∘) − sin (72^∘) is :                    (JEE Main 2022)
(a)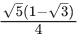
(b)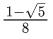
(c)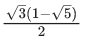
(d)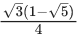

Ans. d
2 sin⁡ 12^∘ − sin⁡ 72^∘
= sin⁡ 12^∘ + (−2cos ⁡42^∘. sin⁡ 30^∘)
= sin⁡ 12^∘ − cos⁡ 42^∘
= sin⁡ 12^∘ − sin⁡ 48^∘
=  sin⁡ 18^∘ . cos 30^∘

Q.12. 16 sin⁡(20^∘)sin⁡(40^∘)sin⁡(80^∘) is equal to:       (JEE Main 2022)
(a) √3
(b) 2√3
(c) 3
(d) 4√3

Ans. b
16 sin⁡ 20^∘ . sin⁡ 40^∘ . sin ⁡80^∘
= 4 sin ⁡60^∘ {∵ 4 sin⁡θ . sin⁡(60^∘ − θ) . sin⁡(60^∘ + θ) = sin⁡ 3θ}
= 2√3

Q.13. The value of cos⁡(2π/7) + cos⁡(4π/7) + cos⁡(6π/7) is equal to :        (JEE Main 2022)
(a) -1
(b)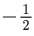
(c)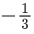
(d)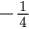

Ans. b

Q.14. α = sin⁡36^∘ is a root of which of the following equation?      (JEE Main 2022)
(a) 16x⁴ − 10x² − 5 = 0
(b) 16x⁴ + 20x² − 5 = 0
(c) 16x⁴ − 20x² + 5 = 0
(d) 16x⁴ − 10x² + 5 = 0

Ans. c
α = sin⁡36^∘ = x (say)

⇒16x² = 10 − 2√5
⇒ (8x² − 5)² = 5
⇒ 16x⁴ − 80x² + 20 = 0
∴ 4x⁴ - 20x² + 5 = 0

Q.15. Let for some real numbers α and β, a = α − iβ. If the system of equations 4i x + (1 + i)y = 0 and 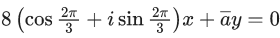 has more than one solution, then α/β is equal to      (JEE Main 2022)
(a) -2√3
(b) 2 - √3
(c) 2 + √3
(d) - 2 - √3

Ans. b
Given a = α − iβ and
4i x + (1 + i)y = 0 ...... (i)

By

By (ii)

Now by (iii) and (iv)

Q.16. If cot α = 1 and sec β = 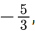 where π < α < 3π/2 and π/2 < β < π, then the value of tan⁡(α + β) and the quadrant in which α + β lies, respectively are :       (JEE Main 2022)
(a) 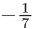 and IV^th quadrant
(b) 7 and I^st quadrant
(c) −7 and IV^th quadrant
(d) 1/7 and I^st quadrant

Ans. a

Q.17. If n is the number of solutions of the equation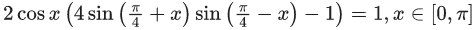
 and S is the sum of all these solutions, then the ordered pair (n, S) is:            (JEE Main 2021)
(a) (3, 13π / 9)
(b) (2, 2π / 3)
(c) (2, 8π / 9)
(d) (3, 5π / 3)

Ans. a



2 cos⁡ x(2 − 4sin²x − 1) = 1
2cos⁡x(1 − 4sin²x) = 1
2cos ⁡x(4cos²x − 3) = 1
4 cos³x − 3cos⁡ x = 1/2
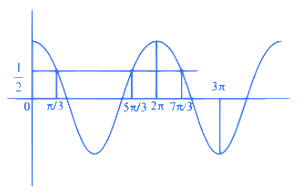
cos⁡ 3x = 1/2
x∈[0, π] ∴ 3x ∈[0, 3π]

Q.18. The number of solutions of the equation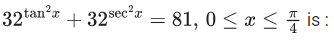
            (JEE Main 2021)
(a) 3
(b) 1
(c) 0
(d) 2

Ans. b



taking log of base 32 both side,


As value of  belongs to (0, 1).
In interval 0 ≤ x ≤ π/4 only one solution.

Q.19. The distance of the point (1, −2, 3) from the plane x − y + z = 5 measured parallel to a line, whose direction ratios are 2, 3, −6 is :            (JEE Main 2021)
(a) 3
(b) 5
(c) 2
(d) 1

Ans. d

(1 + 2λ) + 2 − 3λ + 3 − 6λ = 5
⇒ 6 − 7λ = 5 ⇒ λ = 17

Q.20. 2 sin⁡(π/8) sin⁡(2π/8) sin⁡(3π/8) sin⁡(5π/8) sin⁡(6π/8) sin⁡(7π/8) is :            (JEE Main 2021)
(a) 1/4√2
(b) 1/4
(c) 1/8
(d) 1/8√2

Ans. c

Q.21. The sum of solutions of the equation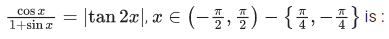
            (JEE Main 2021)
(a)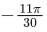
(b) π/10
(c)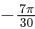
(d)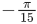

Ans. a

Q.22. If sin ⁡θ + cos⁡θ = 1/2, then 16(sin(2θ) + cos(4θ) + sin(6θ)) is equal to:            (JEE Main 2021)
(a) 23
(b) -27
(c) -23
(d) 27

Ans. c
sin⁡ θ + cos ⁡θ = 1/2
sin²θ + cos²θ + 2sin⁡θ cos⁡θ = 14

Now :
cos⁡4θ = 1 − 2sin²2θ


sin⁡6θ = 3sin⁡ 2θ − 4sin³2θ
= (3 − 4sin²2θ).sin⁡²θ


16[sin⁡ 2θ + cos⁡ 4θ + sin ⁡6θ]

Q.23. The value of cot ⁡π/24 is :           (JEE Main 2021)
(a) √2 + √3 + √2 − √6
(b) √2 + √3 + 2 + √6
(c) √2 − √3 − 2 + √6
(d)  3√2 − √3 − √6

Ans. b

θ = π/24

Q.24. If tan⁡(π/9), x , tan⁡(7π/18) are in arithmetic progression and tan⁡(π/9), y, tan⁡(5π/18) are also in arithmetic progression, then |x − 2y| is equal to:            (JEE Main 2021)
(a) 4
(b) 3
(c) 0
(d) 1

Ans. c

Q.25. The sum of all values of x in [0, 2π], for which sin x + sin 2x + sin 3x + sin 4x = 0, is equal to :            (JEE Main 2021)
(a) 8π
(b) 11π
(c) 12π
(d) 9π

Ans. d
(sin ⁡x + sin ⁡4x) + (sin ⁡2x + sin ⁡3x) = 0






So, sum = 6π + π +2π = 9π

Q.26. If 15 sin⁴α + 10 cos⁴α = 6, for some α ∈ R, then the value of 27 sec⁶α + 8 cosec⁶α is equal to :            (JEE Main 2021)
(a) 500
(b) 400
(c) 250
(d) 350

Ans. c
15 sin²α + 10(1 − sin²α)2 = 6
⇒ 25sin²α − 20sin²α + 4 = 0
⇒ 25sin²α − 10 sin²α − 10 sin²α + 4 = 0
⇒ (5 sin²α − 2)² = 0 ⇒ sin²α = 2/5
∴ cos²α = 3/5

= 125 + 125 = 250

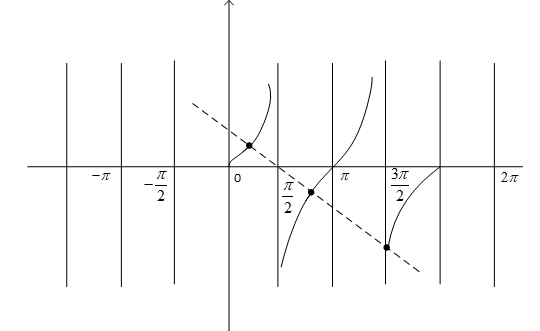
Q.27. The number of solutions of the equation x + 2 tan x = π/2 in the interval [0, 2π] is :            (JEE Main 2021)
(a) 4
(b) 3
(c) 2
(d) 5

Ans. b

x + 2 tan⁡ x = π/2 in [0, 2π]



y = tan⁡ x and y

3 intersection points on the graph.
∴ 3 solutions.

Q.28. If for x ∈ (0, π/2), log₁₀ sin x + log₁₀ cos x = −1 and log₁₀(sin x + cos x) = 1/2(log₁₀ n − 1), n > 0, then the value of n is equal to :            (JEE Main 2021)
(a) 16
(b) 9
(c) 12
(d) 20

Ans. c
log₁₀(sin ⁡x) + log₁₀(cos ⁡x) = −1
sin ⁡x cos ⁡x = 1/10 .... (1)
and log₁₀(sin ⁡x + cos ⁡x) = 1/2(log₁₀n − 1)
⇒ sin⁡x + cos⁡x = (n/10)^1/2
⇒ sin²x + cos²x + 2 sin⁡ x cos⁡ x = n/10 (squaring)

⇒ n/10 = 12/10
⇒ n = 12

Q.29. The number of roots of the equation, 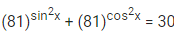 in the interval [0, π] is equal to :            (JEE Main 2021)
(a) 2
(b) 3
(c) 4
(d) 8

Ans. c




t² − 30t + 81 = 0
t² − 27t − 3t + 81 = 0
(t − 3)(t − 27) = 0
t = 3, 27




in [0, π ] sin x > 0


Number of solution = 4

Q.30. If 0 < x, y < π and cosx + cosy − cos(x + y) = 3/2, then sinx + cosy is equal to :            (JEE Main 2021)
(a)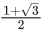
(b) 1/2
(c)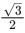
(d)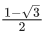

Ans. a


x = y = 60^∘ 

Q.31. All possible values of θ ∈ [0, 2π] for which sin 2θ + tan 2θ > 0 lie in :            (JEE Main 2021)
(a)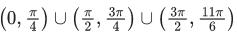
(b)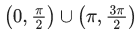
(c)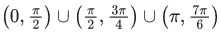
(d)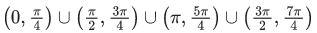

Ans. d

Q.32. If 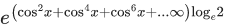satisfies the equation t² - 9t + 8 = 0, then the value of  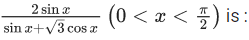           (JEE Main 2021)
(a) √3
(b) 3/2
(c) 2√3
(d) 1/2

Ans. d



Given, t² − 9t + 8 = 0 ⇒ t = 1, 8

Q.33. If y(α) = 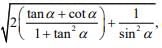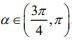then dy/dα at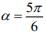is:    (2020)
(a) 4
(b) 4/3
(c) -4
(d) -1/4

Ans. a
We have


(since 1 + tan²α = sec²α)




y(α) = -1 - cotα
Now,

Q.34. If 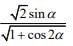= 1/7 and 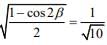, α, β ∈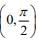, then tan (α + 2β) is equal to ___________.    (2020)

Ans. 1.00
We have
and

Q.35. The value of 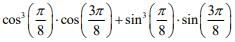is:    (2020)
(a) 1/(√2)
(b) 1/(2√2)
(c) 1/2
(d) 1/4

Ans. b
Given

Q.36. The number of distinct solutions of the equation,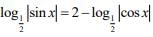in the interval [0, 2π] is_________.    (2020)

Ans. 8.00
Given,
Now,
Hence, there are 8 solutions of the given equation in the interval (0, 2π).

Q.37. If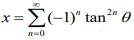 and 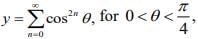then:    (2020)
(a) x(1+y) = 1 
(b) y(1-x) = 1
(c) y(1+x) = 1
(d) x(1-y) = 1

Ans. b
We have
................. (1)

Similarly,
x = cos²θ ..............(2)
From Eqs. (1) and (2), we get

Q.38. For any 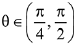 the expression
3(sinθ - cosθ)⁴ + 6(sinθ + cosθ)² + 4sin⁶θ equals:    (2019)
(a) 13 - 4cos²θ + 6sin²θcos²θ
(b) 13 - 4cos⁶θ
(c) 13 - 4cos²θ + 6cos⁴θ
(d) 13 - 4cos⁴θ + 2sin²θcos²θ

Ans. b

Q.39. The value of 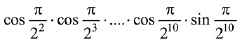   is: (2019)
(a) 1/512
(b) 1/1024
(c) 1/256
(d) 1/2

Ans. a

Q.40. Let 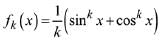 for k = 1, 2, 3,... Then for all x ∈ R, the value of f₄(x)-f₆(x) is equal to:    (2019)
(a) 1/12
(b) 1/4
(c) -1/12
(d) 5/12

Ans. a

= 1/12

Q.41. If sin⁴α + 4 cos⁴β + 2 = 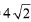 sin α cos β; α, β ∈ [0,π], then cos(α + β) - cos(α - β) is equal to:    (2019)
(a) 0    
(b) -1
(c) √2    
(d) -√2

Ans. d
∵ The given equation is

Then, by A.M., G.M. inequality;
A.M. ≥ G.M.


Inequality still holds when cosβ < 0 but L.H.S. is positive as cosβ > 0, then
L.H.S. = R.H.S

Q.42. 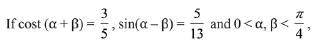 then tan(2α) is equal to:    (2019)
(a) 63/52
(b) 63/16
(c) 21/16
(d) 33/52

Ans. b
∵ α + β and α - β both are acute angles.

⇒ tan (α - β) = 5/12
Now, tan 2α = tan ((α + β) + (α - β))

Q.43. The value of cos²10° - cos10° cos50° + cos²50° is:    (2019)
(a) 3/4 + cos20°
(b) 3/4
(c) 3/2 (1 + cos20°)
(d) 3/2

Ans. b

=3/4

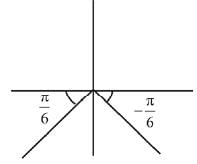
Q.44. Let S = {θ∈[-2 π, 2π] : 2 cos²θ + 3 sinθ = 0}. Then the sum of the elements of S is:    (2019)
(a) 13π/6
(b) 5π/3
(c) 2π
(d) π

Ans. c


The required sum of all solutions in [-2π, 2π] is

Q.45. The value of sin 10° sin 30° sin 50° sin 70° is:    (2019)
(a) 1/16
(b) 1/32
(c) 1/18
(d) 1/36

Ans. a

Q.46. 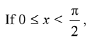 then the number of values of x for which sin x - sin 2x + sin 3x = 0, is:    (2019)
(a) 3    
(b) 1
(c) 4    
(d) 2

Ans. d
sinx - sin2x + sin3x = 0
⇒ sinx - 2 sinx.cosx + 3 sinx - 4 sin³x = 0
⇒ 4 sinx - 4 sin³x - 2 sinx.cosx = 0
⇒ 2 sinx(1-sin²x) - sinx.cosx = 0
⇒ 2 sinx.cos²x - sinx.cosx = 0
⇒ sinx.cosx(2 cosx - 1) = 0

Q.47. The sum of all values of 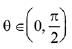 satisfying sin² 2θ + cos⁴ 2θ = 3/4 is:    (2019)
(a) π
(b) 5π/4
(c) π/2
(d) 3π/8

Ans. c


   ...(1)
∵ G.M. ≤ A.M.


= 1/4   ...(2)
So, from eq. (1) & (2), we get
G.M. = A.M.
It is possible only if,

Q.48. All the pairs (x,y) that satisfy the inequality 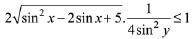 also satisfy the equation:    (2019)
(a) 2|sinx| = 3 sin y    
(b) 2 sin x = sin y
(c) sin x = 2 sin y    
(d) sin x = |sin y|

Ans. d
Given inequality is,

Q.49. The number of solutions of the equation 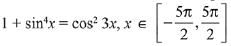 is:    (2019)
(a) 3    
(b) 5    
(c) 7    
(d) 4

Ans. b
Consider equation, 1 + sin⁴x = cos²3x
L.H.S. = 1 + sin⁴x and R.H.S. = cos²3x
∵ L.H.S. ≥ 1 and R.H.S. ≤ 1 ⇒ L.H.S. = R.H.S. = 1
sin⁴x = 0, and cos²3x = 1
⇒ sin x = 0 and (4cos²x - 3)² cos²x = 1
⇒ sin x = 0 and cos²x = 1 ⇒ x = 0, ±π, ±2π
Hence, total number of solutions is 5.

Q.50. Let S be the set of all α ∈ R such that the equation, cos 2x + α sin x = 2α -7 has a solution. Then S is equal to:    (2019)
(a) R
(b) [1,4]    
(c) [3,7]    
(d) [2,6]

Ans. d
Given equation is, cos 2x + α sin x = 2α - 7

Q.51. A value of θ ∈ (0, π/3), for which 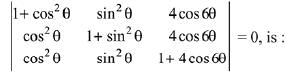    (2019)
(a) π/9
(b) π/18
(c) 7π/24
(d) 7π/36

Ans. a
c₁→ c₁ + c₂ 

Q.52. If [x] denotes the greatest integer ≤ x, then the system of linear equations
[sin θ] x + [-cos θ] y = 0
[cot θ] x + y = 0    (2019)
(a) Have infinitely many solutions if 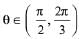 and has a unique solution if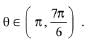 
(b) Has a unique solution if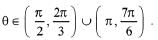
(c) Has a unique solution if 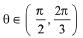 and have infinitely many solutions if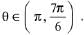
(d) Have infinitely many solutions if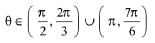

Ans. a
According to the question, there are two cases.

In this interval, [sin θ] = 0, [-cos θ] = 0 and [cot θ] = -1
Then the system of equations will be;
0 · x + 0 · y = 0 and -x + y = 0
Which have infinitely many solutions.

In this interval, [sin θ] = -1 and [-cos θ] = 0,
Then the system of equations will be;
-x + 0 · y = 0 and [cot θ] x + y = 0
Clearly, x = 0 and y = 0 which has unique solution.

Q.53. If sum of all the solution of equation 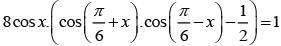 in [0,π ] is kπ,then k is equal to:    (2018)
(a) 2/3
(b) 13/9
(c) 8/9
(d) 20/9

Ans. b

⇒ 6 cos x - 8 cos x sin² x - 4 cos x = 1
⇒ 2 cos x - 8 cos x (1 - cos² x) = 1

Q.54. If tanA and tanB are the roots of the quadratic equation, 3x² - 10x - 25 = 0, then the value of 3 sin²(A +B) - 10 sin(A +B).cos(A+B) - 25 cos²(A + B)    (2018)
(a) -25
(b) 10
(c) -10
(d) 25

Ans. a
Since tanA and tanB are roots of the equation 3x² - 10x - 25 = 0

Q.55. If an angle A of a ΔABC satisfies  5 cosA + 3 = 0, then the roots of the quadratic equaiton, 9x² + 27x + 20 = 0 are:    (2018)
(a) secA, cotA
(b) secA, tanA
(c) tanA, cosA
(d) sinA, secA

Ans. b
5cosA + 3 = 0 ⇒ cosA = -3/5 clearly A ∈ (90º, 180º)
Now roots of equation  9x² + 27x + 20 = 0 are -5/3 and -4/3
⇒ Roots secA and tanA

Q.56. If 5 (tan²x – cos²x) = 2cos 2x + 9, then the value of cos 4x is:    (2017)
(a) -7/9
(b) -3/5
(c) 1/3
(d) 2/9

Ans. a
5 tan²x = 9 cos²x + 7
5 sec²x – 5 = 9 cos²x + 7
Let cos²x = t



cos4x = 2 cos² 2x – 1

Q.57. If 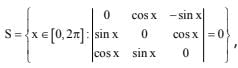 Then 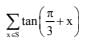    (2017)
(a)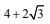
(b)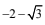
(c)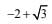
(d)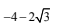

Ans. b

Q.58. If 0 ≤ x < 2π, then the number of real values of x, which satisfy the equation cos x + cos 2x = cos 3x + cos 4x = 0, is    (2016)
(a) 3
(b) 5
(c) 7
(d) 9

Ans. c
We have, cosx + cos2x + cos 3x + cos 4x = 0
(cos x + cos 4x)+ (cos 2x+ cos 3x)= 0



Or


Solutions are

…  (0 ≤ x < 2π)

Q.59. The number of x ∈ [0, 2π] for which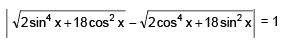 is:    (2016)
(a) 6
(b) 4
(c) 8
(d) 2

Ans. c


Clearly 8 solutions.

Q.60. If A > 0, B > 0 and A + B = π/2 then the minimum value of tanA + tanB is:    (2016)
(a) 2 - √3
(b) 2/√3
(c) √3 - √2
(d) 4 - 2 √3

Ans. d
A, B > 0 and A + B = π/2
Let y = tanA + tanB

Q.61. Let P = {θ : sinθ - cosθ = √2 cos θ} and Q = {θ : sinθ + cos θ = √2 sinθ} be two sets. Then:    (2016)
(a) Q ⊄ P
(b) P ⊄ Q
(c) P ⊂ Q and Q - P ≠ ϕ
(d) P = Q

Ans. d