JEE Main Previous Year Questions (2016- 2024): Probability | Mathematics for EmSAT Achieve PDF Download
Q.1. An unbiased coin is tossed 5 times. Suppose that a variable X is assigned the value k when k consecutive heads are obtained for k = 3, 4, 5, otherwise X takes the value -1. Then the expected value of X, is (2020)
(1) 3/16
(2) 1/8
(3) -3/16
(4) -1/8
Ans. (2)
We have
The expected value of X = ∑ Xp(k)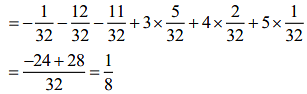
Q.2. In a workshop, there are five machines and the probability of any one of them to be out of service on a day is 1/4. If the probability that at most two machines will be out of service on the same day is (3/4)3 k, then k is equal to (2020)
(1) 17/8
(2) 17/4
(3) 17/2
(4) 4
Ans. (1)
The probability of machine being faulty = 1/4
The probability of machine not being faulty 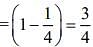
Hence, the probability that at most two machines will be out of service on the same day is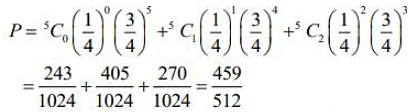
Thus, 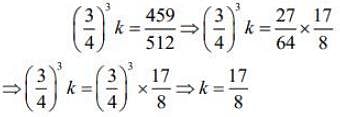
Q.3. Let A and B be two independent events such that P(A) = 1/3 and P(B) = 1/6. Then, which of the following is TRUE? (2020)
(1) P (A/B) = 2/3
(2) P(A/B') = 1/3
(3) P(A'/B') = 1/3
(4) P(A/A ∪ B) = 1/4
Ans. (2)
Given, A and B are two independent events, then
P(A/B) = P(A) = 1/3
P(A/B') = P(A)= 1/3
P(A'/B') = P(A') = 1 - P(A)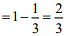
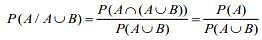
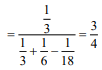
Q.4. If 10 different balls are to be placed in 4 distinct boxes at random, then the probability that two of these boxes contain exactly 2 and 3 balls is (2020)
(1) 965/211
(2) 965/210
(3) 945/210
(4) 945/211
Ans. (3)
Q.5. A random variable X has the following probability distribution:
Then, P (X > 2) is equal to (2020)
(1) 7/12
(2) 1/36
(3) 1/6
(4) 23/36
Ans. (4)
We have 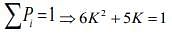
⇒ 6K2 + 5K - 1 = 0 ⇒ (6K - 1)(K + 1)= 0
⇒ K = 1/6 or K = -1(rejected)
Now, P (X > 2) = K + 2K + 5K2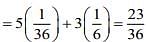
Q.6. Let A and B be two events such that the probability that exactly one of them occurs is 2/5 and the probability that A or B occurs is 1/2, then the probability of both of them occur together is (2020)
(1) 0.02
(2) 0.20
(3) 0.01
(4) 0.10
Ans. (4)
Given,
P(A) + P(B) - 2P(A∩B) = 2/5 ...(1)
and P(A∪B) = 1/2
⇒ P(A) + P(B) - P(A∩B) = 1/2 ...(2)
From Eqs. (1) and (2), we get 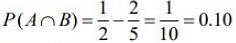
Hence, the probability of both events occur together is 0.10.
Q.7. In a box, there are 20 cards, out of which 10 are labeled as A and the remaining 10 are labeled as B. Cards are drawn at random, one after the other and with replacement, till a second A-card is obtained. The probability that the second A-card appears before the third B-card is (2020)
(1) 9/16
(2) 11/16
(3) 13/16
(4) 15/16
Ans. (2)
The required probability is
Q.8. Ail urn contains 5 red and 2 green balls. A ball is drawn at random from the urn. If the drawn ball is green, then a red ball is added to the urn and if the drawn ball is red, then a green ball is added to the urn; the original ball is not returned to the urn. Now, a second ball is drawn at random from it. The probability that the second ball is red is: (2019)
(1) 21/49
(2) 27/49
(3) 26/49
(4) 32/49
Ans. (4)
Let G represents drawing a green ball and R represents drawing a red ball
So, the probability that second drawn ball is red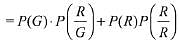
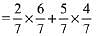
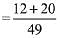
= 32/49
Q.9. An unbiased coin is tossed. If the outcome is a head then a pair of unbiased dice is rolled and the sum of the numbers obtained on them is noted. If the toss of the coin results in tail then a card from a well-shuffled pack of nine cards numbered 1, 2, 3, ..., 9 is randomly picked and the number on the card is noted. The probability that the noted number is either 7 or 8 is: (2019)
(1) 13/36
(2) 15/72
(3) 19/72
(4) 19/36
Ans. (3)
p(Outcome is head) = 1/2
P(Outcome is tail) = 1/2
P( 7 or 8 is the sum of two dice) = 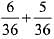 = 11/36
= 11/36
P(7 or 8 is the number of card) 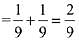
Required probability =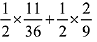
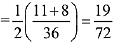
Q.10. If the probability of hitting a target by a shooter, in any shot, is 1/3, then the minimum number of independent shots at the target required by him so that the probability of hitting the target at least once is greater than 5/6, is: (2019)
(1) 3
(2) 6
(3) 5
(4) 4
Ans. (3)
Let the number of independent shots required to hit the target at least once be n, then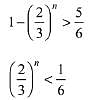
Hence, the above inequality holds when least value of n is 5.
Q.11. Two integers are selected at random from the set {1,2, ...., 11}. Given that the sum of selected numbers is even, the conditional probability that both the numbers are even is: (2019)
(1) 7/10
(2) 1/2
(3) 2/5
(4) 3/5
Ans. (3)
Probability of getting sum of selected two numbers is even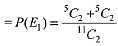
Probability of getting sum is even and selected numbers are also even 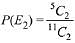
Hence, 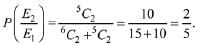
Q.12. Let S = {1, 2, ...., 20}. A subset B of S is said to be “nice”, if the sum of the elements of B is 203. Than the probability that a randomly chosen subset of S is “nice” is: (2019)
(1) 7/220
(2) 5/220
(3) 4/220
(4) 6/220
Ans. (2)
Since total number of subsets of the set S = 220
Now, the sum of all number from 1 to 20 = 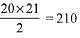
Then, find the sets which has sum 7.
(1) {7}
(2) {1,6}
(3) {2,5}
(4) {3,4}
(5) {1,2,4}
Then, there is only 5 sets which has sum 203
Hence required probability = 5/220
Q.13. In a random experiment, a fair die is rolled until two fours are obtained in succession. The probability that the experiment will end in the fifth throw of the die is equal to: (2019)
(1) 200/65
(2) 150/65
(3) 225/65
(4) 175/65
Ans. (4)
Since, the experiment will end in the fifth throw.
Hence, the possibilities are 4**4 4, *4*4 4, ***4 4
(where * is any number except 4)
Required Probability 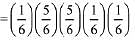
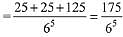
Q.14. In a game, a man wins ₹ 100 if he gets 5 or 6 on a throw of a fair die and loses ₹ 50 for getting any other number on the die. If he decides to throw the die either till he gets a five or a six or to a maximum of three throws, then his expected gain/loss (in rupees) is: (2019)
(1) 400/9 loss
(2) 0
(3) 400/3 gain
(4) 400/3 loss
Ans. (2)
Probability of getting 5 or 6 = P(E) = 2/6 = 1/3
Probability of not getting 5 or 6 = P(E) = 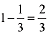
E will consider as success.
His expected gain/loss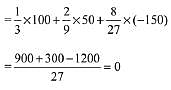
Q.15. In a class of 60 students, 40 opted for NCC, 30 opted for NSS and 20 opted for both NCC and NSS. If one of these students is selected at random, then the probability that the student selected has opted neither for NCC nor for NSS is: (2019)
(1) 1/6
(2) 1/3
(3) 2/3
(4) 5/6
Ans. (1)
P = Set of students who opted for NCC
Q = Set of Students who opted for NSS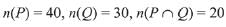
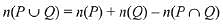
= 40 + 30-20 = 50
∴ Hence, required probability = 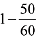 = 1/6
= 1/6
Q.16. Let A and B be two non-null events such that A ⊂ B. Then, which of the following statements is always correct? (2019)
(1) P(A|B) = P(B) - P(A)
(2) P(A|B) ≥ P(A)
(3) P(A|B) ≤ P(A)
(4) P(A|B) = 1
Ans. (2)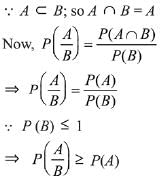
Q.17. The minimum number of times one has to toss a fair coin so that the probability of observing at least one head is at least 90% is: (2019)
(1) 5
(2) 3
(3) 4
(4) 2
Ans. (3)
Let, p is probability for getting head and is probability for getting tail.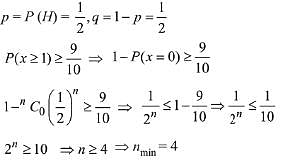
Q.18. Four persons can hit a target correctly with probabilities 1/2, 1/3, 1/4 and 1/8 respectively. If all hit at the target independently, then the probability that the target would be hit, is: (2019)
(1) 25/192
(2) 7/32
(3) 1/192
(4) 25/32
Ans. (4)
P (at least one hit the target) = 1 - P (none of them hit the target)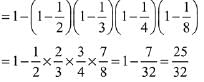
Q.19. Assume that each born child is equally likely to be a boy or a girl. If two families have two children each, then the conditional probability that all children are girls given that at least two are girls is: (2019)
(1) 1/11
(2) 1/10
(3) 1/12
(4) 1/17
Ans. (1)
Let, A = At least two girls
B = All girls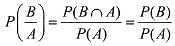
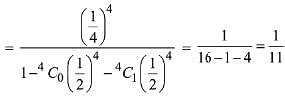
Q.20. Minimum number of times a fair coin must be tossed so that the probability of getting at least one head is more than 99% is: (2019)
(1) 5
(2) 6
(3) 8
(4) 7
Ans. (4)
According to the question,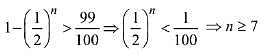
Hence, minimum value is 7.
Q.21. If three of the six vertices of a regular hexazon are chosen at random, then the probability that the triangle formed with these chosen vertices is equilateral is: (2019)
(1) 1/10
(2) 1/5
(3) 3/10
(4) 3/20
Ans. (1)
Total no. of triangles = 6C3
Favorable no. of triangle i.e, equilateral triangles (ΔAEC and ΔBDF) = 2.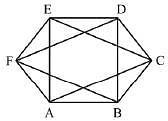
Hence, required probability = 1/10
Q.22. Let a random variable X have a binomial distribution with mean 8 and variance 4. If 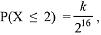 then k is equal to: (2019)
then k is equal to: (2019)
(1) 17
(2) 121
(3) 1
(4) 137
Ans. (4)
Given mean μ = 8 and variance σ2 = 4
⇒ μ = np = 8 and σ2 = npq = 4.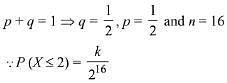
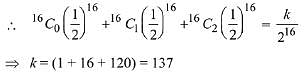
Q.23. For an initial screening of an admission test, a candidate is given fifty problems to solve. If the probability that the candidate can solve any problem is 4/5, then the probability that he is unable to solve less than two problems is: (2019)
(1) 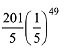
(2) 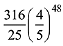
(3) 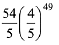
(4) 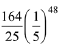
Ans. (3)
Let p is the probability that candidate can solve a problem and q is the probability that candidate can not not solve a problem.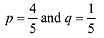 (∵ p + q = 1)
(∵ p + q = 1)
Probability of solving either 50 or 49 problem by the candidate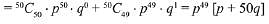
Q.24. A person throws two fair dice. He wins Rs. 15 for throwing a doublet (same numbers on the two dice), wins Rs. 12 when the throw results in the sum of 9, and loses Rs. 6 for any other outcome on the throw. Then the expected gain/loss (in Rs.) of the person is: (2019)
(1) 1/2 gain
(2) 1/4 loss
(3) 1/2 loss
(4) 2 gain
Ans. (3)
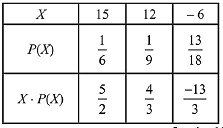
Let X be the random variable which denotes the Rs gained by the person.
Total cases = 6 x 6 = 36.
Favorable cases for the person on winning ₹ 15 are (1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6) i.e., 6 cases.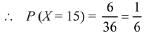
Favorable cases for the person on winning ₹ 12 are (6, 3), (5, 4), (4, 5), (3, 6) i.e., 4.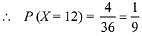
Remaining cases = 36 - 6 - 4 = 26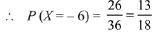
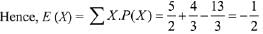
Q.25. A bag contains 4 red and 6 black balls. A ball is drawn at random from the bag, its colour is observed and this ball along with two addit ional balls of the same colour is returned to the bag. If now a ball is drawn at random from the bag, then probability that this drawn ball is red, is: (2018)
(1) 3/10
(2) 2/5
(3) 1/5
(4) 3/4
Ans. (2)
Initially 4 Red balls and 6-Black balls
Required probability = 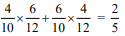
Q.26. A box 'A' contains 2 white, 3 red and 2 black balls. Another box 'B' contains 4 white, 2 red and 3 black balls. If two balls are drawn at random, without replacement, from a randomly selected box and one ball turns out to be white while the other ball turns out to be red, then the probability that both balls are drawn from box 'B' is: (2018)
(1) 9/16
(2) 9/32
(3) 7/8
(4) 7/16
Ans. (4)
Probability that box A is selected P(A) = 1/2
Probability that box B is selected P(B) = 1/2
E be event that one ball is white while the other is red
P(E) = P(A) . P(E/A) + P(B) P(E/B)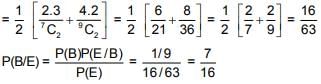
Q.27. Two different families A and B are blessed with equal number of children. There are 3 tickests to be distributed amongst the children of these families so that no child gets more than one ticket. If the probability that all the tickets go to the children of the family B is 1/12, then the number of children in each family is: (2018)
(1) 6
(2) 5
(3) 3
(4) 4
Ans. (2)
Let the number of children in each family be x. Thus the total number of children in both the families are 2x.
Now, it is given that 3 tickets are distributed amongst the children of these two families.
Thus, the probability that all the three tickets go to the children in family B.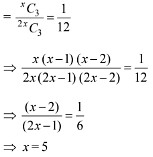
Thus, the number of children in each family is 5.
Q.28. Let A, B and C be three events, which are pair-wise independent and  denotes the complement of an event E. If P(A∩B∩C) = 0 and P(C) > 0, then
denotes the complement of an event E. If P(A∩B∩C) = 0 and P(C) > 0, then 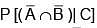 is equal to: (2018)
is equal to: (2018)
(1) 
(2) 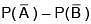
(3) 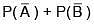
(4) 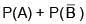
Ans. (1)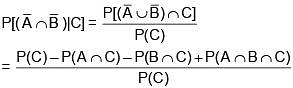
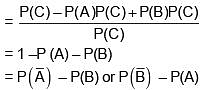
Q.29. A box contains 15 green and 10 yellow balls. If 10 balls are randomly drawn, one-by-one, with replacement, then the variance of the number of green balls drawn is (2017)
(1) 6/25
(2) 12/5
(3) 6
(4) 4
Ans. (2)
n = 10
p(Probability of drawing a green ball) = 15/25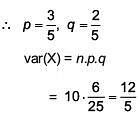
Q.30. If two different numbers are taken from the set {0, 1, 2, 3, ......, 10}; then the probability that their sum as well as absolute difference are both multiple of 4, is (2017)
(1) 7/55
(2) 6/55
(3) 12/55
(4) 14/55
Ans. (2)
Total number of ways = 11C2 = 55
Favourable ways are
(0, 4), (0, 8), (4, 8), (2, 6), (2, 10), (6, 10)
Probability = 6/55
Q.31. For three events A, B and C, P (Exactly one of A or B occurs) = P(Exactly one of B or C occurs) = P (Exactly one of C or A occurs) = 1/4 and P(All the three events occur simultaneously) = 1/16 Then the probability that at least one of the events occurs, is (2017)
(1) 3/16
(2) 7/32
(3) 7/16
(4) 7/64
Ans. (3)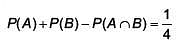
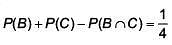
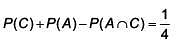
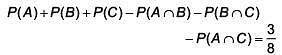
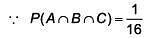
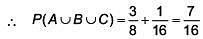
Q.32. Three persong P, Q and R independently try to hit a target. If the probabilities of their hitting the target are 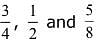 respectively, then the probability that the target is hit by P or Q but not by R is: (2017)
respectively, then the probability that the target is hit by P or Q but not by R is: (2017)
(1) 39/64
(2) 21/64
(3) 9/64
(4) 15/64
Ans. (2)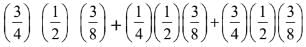
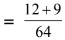
= 27/64
Q.33. An unbiased coin is tossed eight times. The probabiity of obtaining at least one head and at least one tail is: (2017)
(1) 127/128
(2) 63/64
(3) 255/256
(4) 1/2
Ans. (1)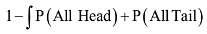
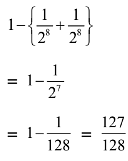
Q.34. From a group of 10 men and 5 women, four member committees are to be formed each of which must contain at least one women. Then the probability for these committees to have more women than men, is: (2017)
(1) 3/11
(2) 2/23
(3) 1/11
(4) 21/220
Ans. (3)
Probability of 4 member committee which contain atleast one woman.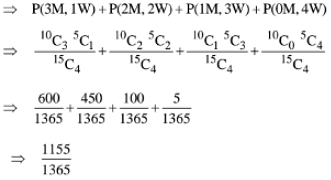
Probability of committees to have more women than men.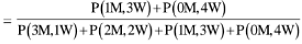
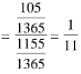
Q.35. Let E and F be two independent events. The probability that both E and F happen is 1/12 and the probability that neither E nor F happens is 1/2, then a value of P(E)/P(F) is: (2017)
(1) 4/3
(2) 1/3
(3) 3/2
(4) 5/12
Ans. (1)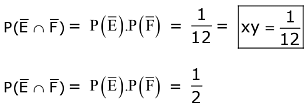
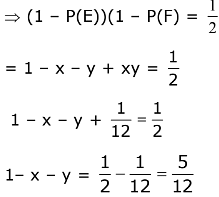
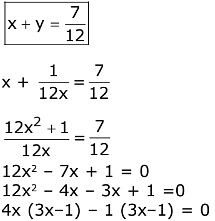
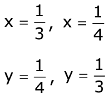
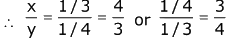
Q.36. Let two fair six-faced dice A and B be thrown simultaneously. If E1 is the event that die A shows up four, E2 is the event that die B shows up two and E3 is the event that the sum of numbers on both dice is odd, then which of the following statements is NOT true? (2016)
(1) E1 and E2 are independent
(2) E2 and E3 are independent
(3) E1 and E3 are independent
(4) E1, E2 and E3 are independent
Ans. (4)
P(E1) = 1/6
P(E2) = 1/6
P(E3) = 1/2
P(E1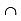 E2) = 1/36
E2) = 1/36
P(E2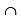 E3) = 1/12
E3) = 1/12
P(E3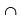 E1) = 1/12
E1) = 1/12
P(E1 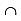 E2
E2 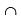 E3) = 0
E3) = 0
∴ E1, E2, E3 are not independent
Q.37. If A and B are any two events such that P(A) =2/5 and P(A ∩ B) = 3/20, then the conditional probability, P(A/(A' ∪ B')), where A' denotes the complement of A, is equal to: (2016)
(1) 8/17
(2) 1/4
(3) 5/17
(4) 11/20
Ans. (3)
P(A) = 2/5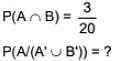

Q.38. An experiment succeeds twice as often as it fails. The probability of at least 5 successes in the six trials of this experiment is (2016)
(1) 192/729
(2) 256/729
(3) 240/729
(4) 496/729
Ans. (2)
Given = p = 2q & we know that p+q = 1
⇒ P = 2/3, q = 1/3
The problem of at least 5 successes
= 6C5 P5 q + 6C6 P6 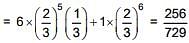
|
141 videos|213 docs|254 tests
|


















