JEE Main Previous Year Questions (2016- 2025): Vector Algebra and Three Dimensional Geometry | Mathematics for NDA PDF Download
Q.1. A vector 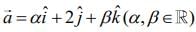 lies in the plane of the vectors
lies in the plane of the vectors 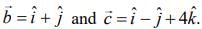 If
If 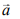 bisects the angle between
bisects the angle between  then (2020)
then (2020)
(1) 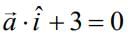
(2) 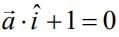
(3) 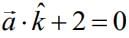
(4) 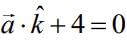
Ans. (3)
We have,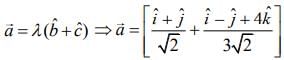
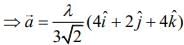
On comparing with 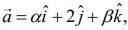
We get α = 4 and β = 4
Therefore, 
Now, again consider 
On comparing with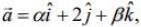 we get
we get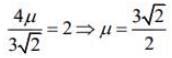
Therefore, 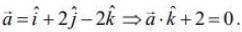
Q.2. Let 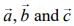 be three unit vectors such that
be three unit vectors such that 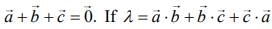 and
and 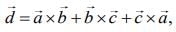 then the ordered pair,
then the ordered pair, 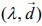 is equal to (2020)
is equal to (2020)
(1) 
(2) 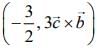
(3) 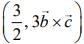
(4) 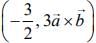
Ans. (4)
Given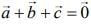 ...(1)
...(1)
Taking square of both sides, we get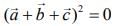
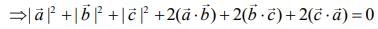
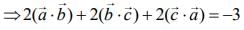 (since
(since 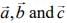 are unit vectors)
are unit vectors)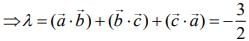
Now,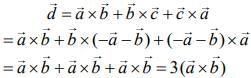
Q.3. Let 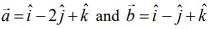 be two vectors. If
be two vectors. If 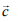 is a vector such that
is a vector such that 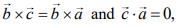 then
then 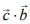 is equal to (2020)
is equal to (2020)
(1) -3/2
(2) 1/2
(3) -1/2
(4) -1
Ans. (3)
Given 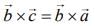
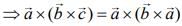
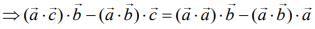 ...(1)
...(1)
Now, 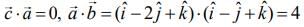
and 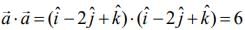
Substituting these values in Eq. (1), we get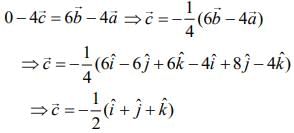
Hence, 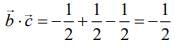
Q.4. The projection of the line segment joining the points (1, −1, 3) and (2, −4, 11) on the line joining the points (−1, 2, 3) and (3, −2, 10) is _____. (2020)
Ans. (8.00)
We have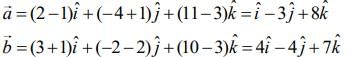
Hence, the required projection is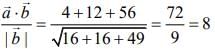
Q.5. If the vectors 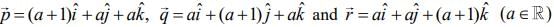 are coplanar and
are coplanar and 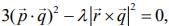 then the value of λ is _____. (2020)
then the value of λ is _____. (2020)
Ans. (1.00)
The vectors 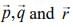 are coplanar vectors, then
are coplanar vectors, then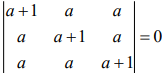
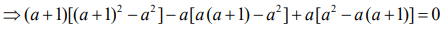
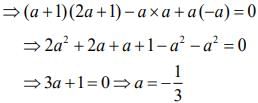
Therefore, 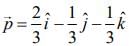 ...(1)
...(1)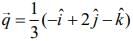 ...(2)
...(2)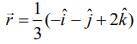 ...(3)
...(3)
Now, 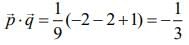 ...(4)
...(4)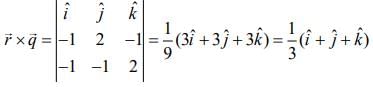
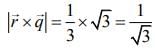 ...(5)
...(5)
Hence, 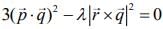
Q.6. Let 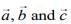 be three vectors such that
be three vectors such that 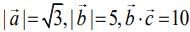 and the angle between
and the angle between 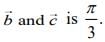 If
If 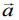 is perpendicular to the vector
is perpendicular to the vector 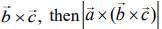 is equal to ____. (2020)
is equal to ____. (2020)
Ans. (30.00)
Given, 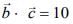
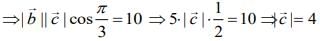
Now, 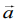 is perpendicular to the vector
is perpendicular to the vector 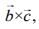 then
then 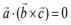
Hence,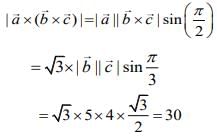
Q.7. If the distance between the plane 23x - 10y - 2z + 48 =0 and the plane containing the lines 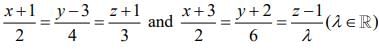 is equal to
is equal to 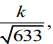 then k is equal to _____. (2020)
then k is equal to _____. (2020)
Ans. (3.00)
The given lines must be intersecting
Therefore,
(2s - 1, 3s + 3, 8s - 1) = (2t - 3t, t - 2, λt + 1)
Now, 2s - 1 = 2t - 3 ...(1)
3s + 3 = t - 2 ...(2)
8s - 1 = λt + 1 ...(3)
On solving above equations, we get
t = -1, s = -2 and λ = 18
Distance of plane contains given lines from given plane is same as distance between point (–3, –2, 1) from given plane. So,
Q.8. Let P be a plane passing through the points (2, 1, 0), (4, 1, 1) and (5, 0, 1) and R be any point (2, 1, 6). Then, the image of R in the plane P is (2020)
(1) (6, 5, 2)
(2) (6, 5, −2)
(3) (4, 3, 2)
(4) (3, 4, −2)
Ans. (2)
The equation of the plane passing through the points (2, 1, 0), (4, 1, 1) and (5, 0, 1) is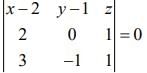
⇒ (x - 2)(1) - (y - 1)(2 - 3) + z(-2) = 0
⇒ x + y - 2z = 3
Let I and F are respectively image and foot of perpendicular of point R in the plane. So, the equation of RI is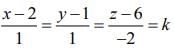 (say)
(say)
⇒ x = k + 2, y = k + 1 and z = -2k + 6
Hence, the coordinates of point F is 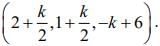
Point F lies in the plane, then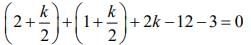
⇒ 3k = 12 ⇒ k = 4
Hence, the image I is (6, 5, -2).
Q.9. If the foot of the perpendicular drawn from the point (1, 0, 3) on a line passing through (α, 7, 1) is 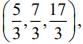 then α is equal to _____.
then α is equal to _____.
Ans. (4.00)
We have,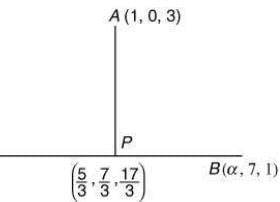
Direction ratio of BP 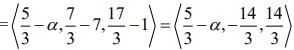
Direction ratio of AP =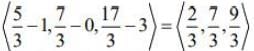
Since AP and BP are perpendicular, then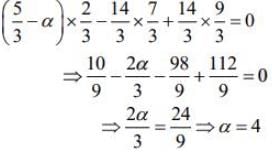
Q.10. The shortest distance between the lines 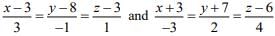 is (2020)
is (2020)
(1) 2√30
(2) 7/2 (√30)
(3) 3√30
(4) 3
Ans. (3)
The equations of the lines are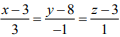 ...(1)
...(1)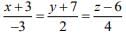 ...(2)
...(2)
The distance between the lines is given by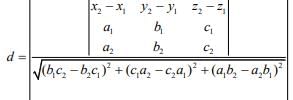
Now,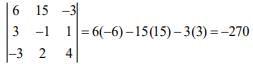
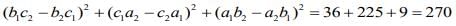
Hence,
Q.11. Let the volume of a parallelepiped whose coterminous edges are given by 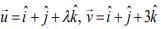 and
and 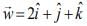 be 1 cu. unit. If θ be the angle between the edges
be 1 cu. unit. If θ be the angle between the edges  then cos θ can be (2020)
then cos θ can be (2020)
(1) 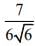
(2) 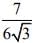
(3) 5/7
(4) 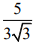
Ans. (2)
The volume of parallelepiped is 1 cu. unit. Therefore,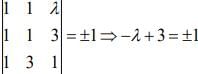
⇒ λ = 2, 4
Now, 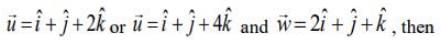
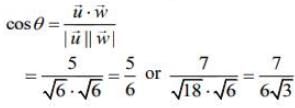
Q.12. The mirror image of the point (1, 2, 3) in a plane is 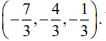 Which of the following points lies on this plane? (2020)
Which of the following points lies on this plane? (2020)
(1) (1, 1, 1)
(2) (1, -1, 1)
(3) (-1, -1, 1)
(4) (-1, -1, -1)
Ans. (2)
Direction ratios of normal to the plane is
<1 + (7/3), 2 + (4/3),3 + (1/3)> = <1, 1, 1>
The coordinates of mid- point of image and point is 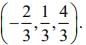
The equation of plane is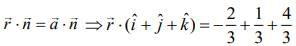
⇒ x + y + z = 1
Hence, the point (1, −1, 1) lies on the plane.
Q.13. If for some α and β in 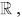 the intersection of the following three planes
the intersection of the following three planes
x + 4y - 2z =1
x + 7y - 5z = β
x + 5y - αz = 5
is a line in 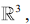 then α + β is equal to (2020)
then α + β is equal to (2020)
(1) 0
(2) 10
(3) 2
(4) −10
Ans. (2)
We have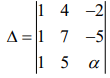 =0
=0
⇒ (7α + 25) - (4α + 10) + (-20 + 14) = 0
⇒ 3α + 9 = 0 ⇒ α = -3
and 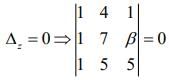
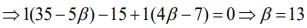
Hence, α + β = -3 + 13 = 10
Q.14. Let 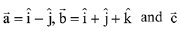 be a vector such that
be a vector such that 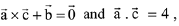 then
then 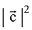 is equal to: (2019)
is equal to: (2019)
(1) 19/2
(2) 9
(3) 8
(4) 17/2
Ans. (1)
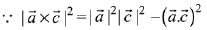

Q.15. Let 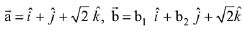 and
and 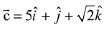 be three vectors such that the projection vector of
be three vectors such that the projection vector of 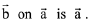
If 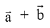 is perpendicular to
is perpendicular to  is equal to: (2019)
is equal to: (2019)
(1) √32
(2) 6
(3) √22
(4) 4
Ans. (2)
Projection of 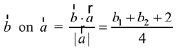
According to question 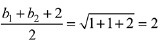
⇒ b1 + b2 = 2 ...(1)
Since, 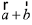 is perpendicular to
is perpendicular to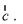
Hence 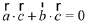
⇒ 8 + 5b1 + b2 + 2 = 0 ...(2)
From (1) and (2),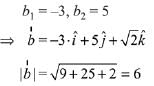
Q.16. Let 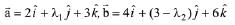 and
and 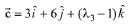 be three vectors such that
be three vectors such that 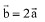 and
and 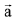 is perpendicular to
is perpendicular to 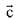 Then a possible value of (λ1, λ2, λ3) is: (2019)
Then a possible value of (λ1, λ2, λ3) is: (2019)
(1) (1, 3, 1)
(2) (-1/2, 4, 0)
(3) (1/2, 4, -2)
(4) (1, 5, 1)
Ans. (2)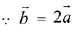
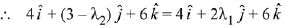
∴ 3 - λ2 = 2λ1 ...(1)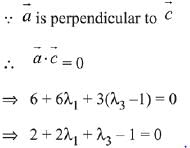
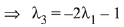 ...(2)
...(2)
Since, (-1/2, 4, 0) satisfies equation (1) and (2). Hence, one of possible value of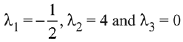
Q.17. Let 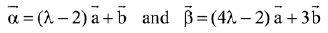 be two given vectors where vectors
be two given vectors where vectors 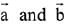 are non-collinear. The value of λ for which vectors
are non-collinear. The value of λ for which vectors 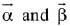 are collinear, is: (2019)
are collinear, is: (2019)
(1) -4
(2) -3
(3) 4
(4) 3
Ans. (1)
Let 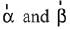 are collinear for same k
are collinear for same k
i.e., 
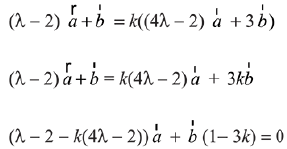
But 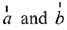 are non-collinear, then
are non-collinear, then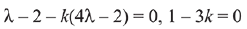
⇒ 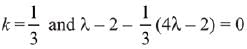
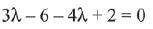
λ = -4
Q.18. Let 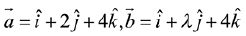 and
and 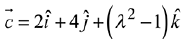 be coplanar vectors. Then the non-zero vector
be coplanar vectors. Then the non-zero vector 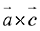 is: (2019)
is: (2019)
(1) 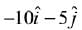
(2) 
(3) 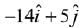
(4) 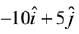
Ans. (4)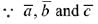 are coplanar
are coplanar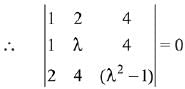
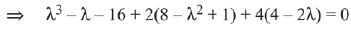
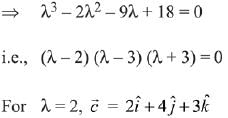

For 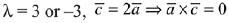 (Rejected)
(Rejected)
Q.19. Let 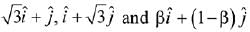 respectively be the position vectors of the points A, B and C with respect to the origin O. If the distance of C from the bisector of the acute angle between OA and OB is 3/√2, then the sum of all possible values of β is: (2019)
respectively be the position vectors of the points A, B and C with respect to the origin O. If the distance of C from the bisector of the acute angle between OA and OB is 3/√2, then the sum of all possible values of β is: (2019)
(1) 4
(2) 3
(3) 2
(4) 1
Ans. (4)
Since, the angle bisector of acute angle between OA and OB would be y = x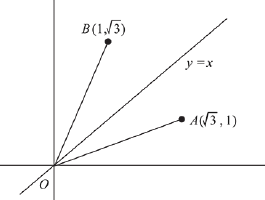
Since, the distance of C from bisector = 3/√2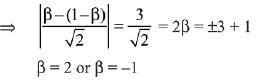
Hence, the sum of all possible value of β = 2 + (-1) = 1
Q.20. The sum of the distinct real values of μ, for which the vectors, 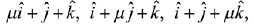 are co-planar, is: (2019)
are co-planar, is: (2019)
(1) -1
(2) 0
(3) 1
(4) 2
Ans. (1)
∵ Three vectors 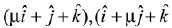 and
and 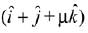 are copalnar.
are copalnar.
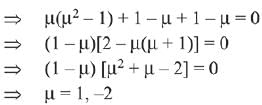
Therefore, sum of all real values = 1 - 2 = -1
Q.21. Let  be three unit vectors, out of which vectors
be three unit vectors, out of which vectors  are non-parallel. If α and β are the angles which vector
are non-parallel. If α and β are the angles which vector 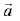 makes with vectors
makes with vectors 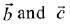 respectively and
respectively and 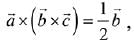 then
then 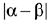 is equal to: (2019)
is equal to: (2019)
(1) 30°
(2) 90°
(3) 60°
(4) 45°
Ans. (1)
Since,  are three unit vectors
are three unit vectors
∴ 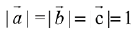
Then, 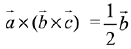
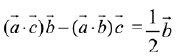
∴ 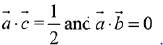
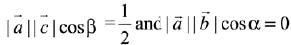
⇒ β = 60° and α = 90°
Hence, 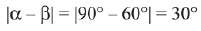
Q.22. The magnitude of the projection of the vector 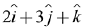 on the vector perpendicular to the plane containing the vectors
on the vector perpendicular to the plane containing the vectors 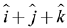 and
and 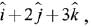 is: (2019)
is: (2019)
(1) √3/2
(2) √6
(3) 3√6
(4) 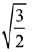
Ans. (4)
Let 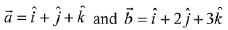
∴ Vector perpendicular to 
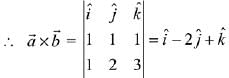
Now, projection of vector 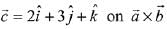 is
is 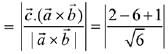
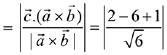
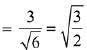
Q.23. Let 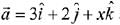 and
and 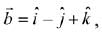 for some real x. Then
for some real x. Then 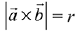 is possible if: (2019)
is possible if: (2019)
(1) 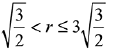
(2) 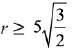
(3) 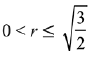
(4) 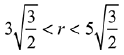
Ans. (2)
Given 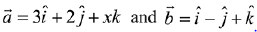
Now, 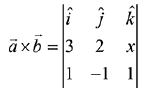
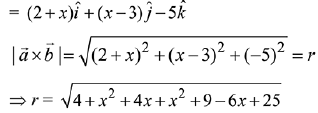
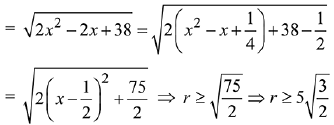
Q.24. Let  where
where  is parallel to
is parallel to 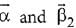 is perpendicular to
is perpendicular to 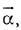 then
then 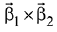 is equal to: (2019)
is equal to: (2019)
(1) 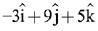
(2) 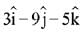
(3) 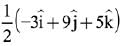
(4) 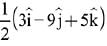
Ans. (3)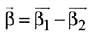 ...(1)
...(1)
Since, 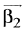 is perpendicular to
is perpendicular to 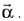
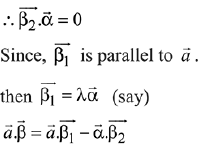
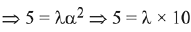
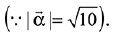
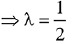
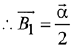
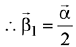
Cross product with 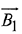 in equation (1)
in equation (1)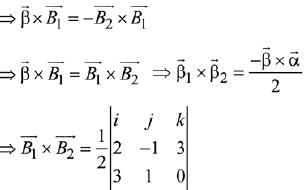
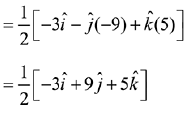
Q.25. If a unit vector 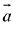 makes angles π/3 with
makes angles π/3 with 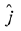 and θ ∈ (0, π) with
and θ ∈ (0, π) with 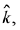 then a value of 0 is: (2019)
then a value of 0 is: (2019)
(1) 5π/6
(2) π/4
(3) 5π/12
(4) 2π/3
Ans. (4)
Let cos α, cos β, cos γ be direction cosines of a.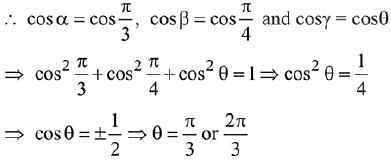
Q.26. The distance of the point having position vector 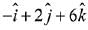 from the straight line passing through the point (2, 3, -4) and parallel to the vector,
from the straight line passing through the point (2, 3, -4) and parallel to the vector, 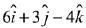 is: (2019)
is: (2019)
(1) 7
(2) 4√3
(3) 6
(4) 2√13
Ans. (1)
Equation of the line is 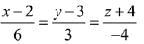
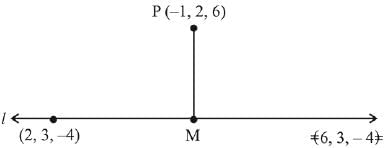
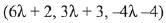
Let the point M on the line l is (6λ + 2, 3λ + 3, -4λ - 4)
Direction ratio's of PM is (6λ + 3, 3λ + 1, - 4λ- 10)
⇒ (6λ + 3) (6) + (3λ + 1) (3) + (-4λ.- 10) (- 4) = 0
⇒ λ = - 1 ⇒ M = (- 4, 0, 0)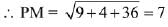
Q.27. Let a = 3i + 2j + 2k and b = i + 2j - 2k be two vectors. If a vector perpendicular to both the vectors  has the magnitude 12 then one such vector is: (2019)
has the magnitude 12 then one such vector is: (2019)
(1) 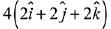
(2) 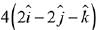
(3) 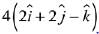
(4) 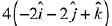
Ans. (2)
Let vector be 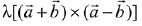
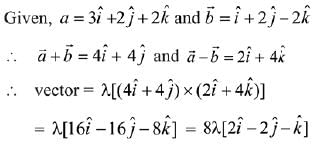
Given that magnitude of the vector is 12.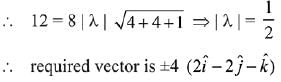
Q.28. Let α ∈ R and the three vectors 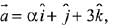
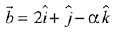 and
and 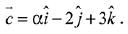 Then the set
Then the set 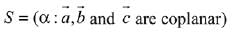 (2019)
(2019)
(1) is singleton
(2) is empty
(3) contains exactly two positive numbers
(4) contains exactly two numbers only one of which is positive
Ans. (2)
Let, three vectors 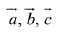 are coplanar, then
are coplanar, then 
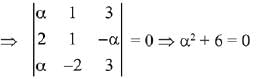
∵ no real value of ‘α’ exist,
∴ set S is an empty set.
Q.29. The equation of the line passing through (-4, 3, 1), parallel to the plane x + 2y - z - 5 = 0 and intersecting the line 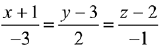 is: (2019)
is: (2019)
(1) 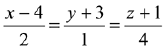
(2) 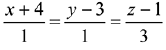
(3) 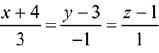
(4) 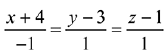
Ans. (3)
Let any point on the intersecting line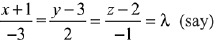
is (-3λ - 1, 2λ + 3, -λ + 2)
Since, the above point lies on a line which passes through the point (-4, 3, 1)
Then, direction ratio of the required line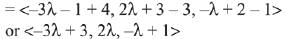
Since, line is parallel to the plane
x + 2y - z - 5 = 0
Then, perpendicular vector to the line is 
Now (-3λ + 3)(1) + (2λ)(2) + (-λ + 1)(-1) = 0
⇒ λ = - 1
Now direction ratio of the required line = <6, - 2, 2 > or <3,-1, 1>
Hence required equation of the line is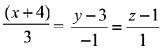
Q.30. The plane through the intersection of the planes x + y + z = 1 and 2x + 3y-z + 4 = 0 and parallel to j-axis also passes through the point: (2019)
(1) (-3, 0, -1)
(2) (-3, 1, 1)
(3) (3, 3, -1)
(4) (3, 2, 1)
Ans. (4)
Since, equation of plane through intersection of planes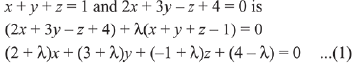
But, the above plane is parallel to y-axis then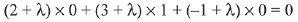
⇒ λ = -3
Hence, the equation of required plane is
-x - 4z + 7 = 0
⇒ x + 4z - 7 = 0
Therefore, (3, 2, 1) the passes through the point.
Q.31. The equation of the plane containing the straight line 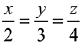 and perpendicular to the plane containing the straight lines
and perpendicular to the plane containing the straight lines 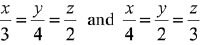 is: (2019)
is: (2019)
(1) x - 2y + z = 0
(2) 3x + 2y - 3z = 0
(3) x + 2y - 2z = 0
(4) 5x + 2y - 4z = 0
Ans. (1)
Let the direction ratios of the plane containing lines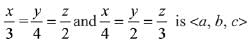
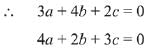
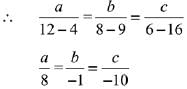
∴ Direction ratio of plane = <-8, 1, 10>.
Let the direction ratio of required plane is <l, m, n>
Then-81 + m + 10n = 0 ...(1)
and 2l + 3m + 4n = 0 ...(2)
From (1) and (2),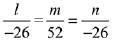
∴ D.R.s are <1, -2, 1>
∴ Equation of plane: x - 2y + z = 0
Q.32. The plane passing through the point (4, -1, 2) and parallel to the lines  also passes through the point: (2019)
also passes through the point: (2019)
(1) (1, 1, -1)
(2) (1, 1, 1)
(3) (-1, -1,-1)
(4) (-1, -1, 1)
Ans. (2)
Equation of required plane is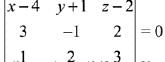
(x - 4)(-3 -4) - (y + 1)(9 - 2) + (z - 2) (6 + 1) = 0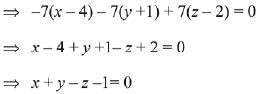
∵ point (1, 1, 1) satisfies this equation
∴ point (1, 1, 1) lies on the plane
Q.33. Let A be a point on the line  and B(3, 2, 6) be a point in the space. Then the value of μ for which the vector
and B(3, 2, 6) be a point in the space. Then the value of μ for which the vector 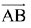 is parallel to the plane x - 4y + 3z = 1 is: (2019)
is parallel to the plane x - 4y + 3z = 1 is: (2019)
(1) 1/4
(2) 1/8
(3) 1/2
(4) -1/4
Ans. (1)
∵ A be a point on given line.
∴ Position vector of A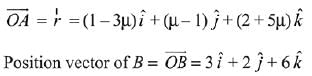
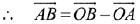
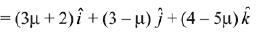
Equation of plane is: x - 4y + 3z = 1
∵ 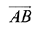 is parallel to this plane.
is parallel to this plane.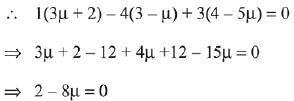
⇒ μ = 1/4
Q.34. The plane which bisects the line segment joining the points (- 3, - 3, 4) and (3, 7, 6) at right angles, passes through which one of the following points? (2019)
(1) (-2, 3, 5)
(2) (4, -1, 7)
(3) (2, 1, 3)
(4) (4, 1, -2)
Ans. (4)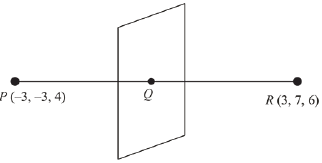
Q(0, 2, 5)
Since, direction ratios of normal to the plane is
Then, equation of the plane is
(x - 0)6 + (y - 2)10 + (z - 5)2 = 0
3x + 5y - 10 + z - 5 = 0
3x + 5y + z = 15 ...(1)
Since, plane (1) satisfies the point (4, 1, -2)
Hence, required point is (4, 1, -2)
Q.35. On which of the following lines lies the point of inter-section of the line, 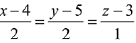 and the plane, x + y + z = 2? (2019)
and the plane, x + y + z = 2? (2019)
(1) 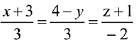
(2) 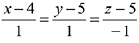
(3) 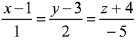
(4) 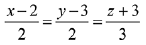
Ans. (3)
Let any point on the line 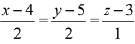 be A(2λ + 4, 2λ + 5, λ, + 3) which lies on the plane x +y + z = 2
be A(2λ + 4, 2λ + 5, λ, + 3) which lies on the plane x +y + z = 2
⇒ 2λ + 4 + 2λ + 5 + λ + 3 = 2
⇒ 5λ = -10 ⇒ λ = - 2
Then, the point of intersection is (0, 1, 1)
which lies on the line 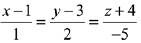
Q.36. The plane containing the line 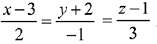 and also containing its projection on the plane 2x + 3y- z = 5, contains which one of the following points? (2019)
and also containing its projection on the plane 2x + 3y- z = 5, contains which one of the following points? (2019)
(1) (2, 2, 0)
(2) (-2, 2, 2)
(3) (0, -2, 2)
(4) (2, 0, -2)
Ans. (4)
Let normal to the required plane is 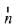
⇒ 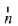 is perpendicular to both vector
is perpendicular to both vector 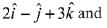
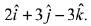
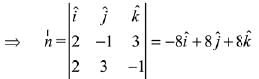
⇒ Equation of the required plane is
⇒ (x - 3)(-8) + (y + 2) x 8 + (z - 1) x 8 = 0
⇒ (x - 3) (-1) + (y + 2) x 1 + (z - 1) x 1 = 0
⇒ x - 3 - y - 2 - z + 1 =0
∵ x - y - z = 4 passes through (2, 0, -2)
∴ plane contains (2, 0, -2).
Q.37. The direction ratios of normal to the plane through the points (0, -1, 0) and (0,0, 1) and making an angle π/4 with the plane y - z + 5 = 0 are: (2019)
(1) 2, -1, 1
(2) 2, √2, -√2
(3) √2, 1, -1
(4) 2√3, 1, -1
Ans. (2, 3)
Let the d.r’s of the normal be (a, b, c)
Equation of the plane is
a(x - 0) + b(y + 1) + c(z - 0) = 0
∵ It passes through (0, 0, 1)
∴ b + c
Also 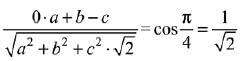
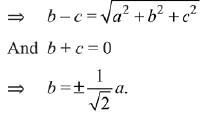
∴ The d.r’s are √2, 1, -1 or 2, √2, -√2
Q.38. Two lines 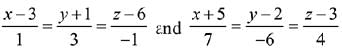 intersect at the point R. The reflection of R in the xy-plane has coordinates: (2019)
intersect at the point R. The reflection of R in the xy-plane has coordinates: (2019)
(1) (2, -4, -7)
(2) (2, 4, 7)
(3) (2, -4, 7)
(4) (-2, 4, 7)
Ans. (1)
Let the coordinate of P with respect to line
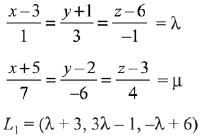
and coordinate of P w.r.t.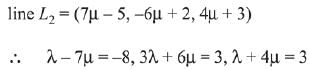
From above equation : λ = -1, μ = 1 .
∴ Coordinate of point of intersection R = (2, -4, 1).
Image of R w.r.t. xy plane = (2, -4, -7).
Q.39. If the point (2, α, β) lies on the plane which passes through the points (3,4, 2) and (7, 0, 6) and is perpendicular to the plane 2x-5y = 15, then 2α - 3β is equal to: (2019)
(1) 12
(2) 7
(3) 5
(4) 17
Ans. (2)
Let the normal to the required plane is n, then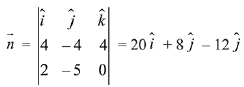
∴ Equation of the plane
(x - 3) x 20 + (y - 4) x 8 + (z - 2) x (-12) = 0
5x - 15 + 2y - 8 - 3z + 6 = 0
5x + 2y - 3z - 17 = 0 ...(1)
Since, equation of plane (1) passes through (2, α, β), then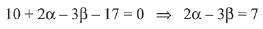
Q.40. The perpendicular distance from the origin to the plane containing the two lines, 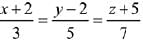 and
and 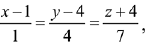 is: (2019)
is: (2019)
(1) 11√6
(2) 11/√6
(3) 11
(4) 6/√11
Ans. (2)
∵ plane containing both lines.
∴ D.R. of plane 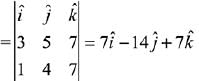
Now, equation of plane is,
7(x - 1) - 14(y - 4) + 7 (z + 4) = 0
⇒ x - 1 - 2y + 8 + z + 4 = 0
⇒ x - 2y + z + 11 = 0
Hence, distance from (0, 0, 0) to the plane,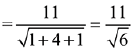
Q.41. If an angle between the line, 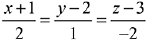 and the plane, x - 2y - kx = 3 is
and the plane, x - 2y - kx = 3 is 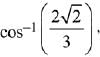 then a value of k is (2019)
then a value of k is (2019)
(1) 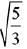
(2) 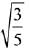
(3) -3/5
(4) -5/3
Ans. (1)
Let angle between line and plane is θ, then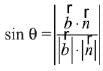
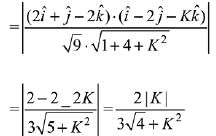
Since, 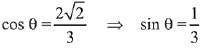
Then, 
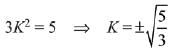
Q.42. Let S be the set of all real values of λ such that a plane passing through the points {-λ2, 1, 1), (1, -λ2, 1) and (1, 1, -λ2) also passes through the point-(-1,-1, 1). Then S is equal to: (2019)
(1) {√3}
(2) {√3, -√3}
(3) {1, -1}
(4) {3, -3}
Ans. (2)
Let 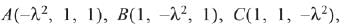 D(-1, -1, 1) lie on same plane, then
D(-1, -1, 1) lie on same plane, then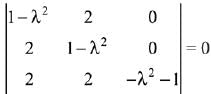
⇒ (λ2 + 1)((1 -λ2)2 -4) = 0
⇒ (3 - λ2)(λ2 + 1) = 0 ⇒ λ2 = 3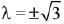
Hence, S = {-√3, √3}
Q.43. The equation of a plane containing the line of intersection of the planes 2x - y - 4 = 0 and y + 2z - 4 = 0 and passing through the point (1, 1, 0) is: (2019)
(1) x- 3y- 2z = -2
(2) 2x - z = 2
(3) x - y - z = 0
(4) x + 3y + z = 4
Ans. (3)
Let the equation of required plane be;
(2x - y - 4) + λ(y + 2z - 4) = 0
∴ This plane passes through the point (1, 1, 0) then (2 - 1 - 4) + λ(1 + 0 - 4) = 0
⇒ λ = -1
Then, equation of required plane is,
(2x - y - 4) - (y + 2z - 4) = 0
⇒ 2x - 2y — 2z = 0 ⇒ x - y - z = 0
Q.44. The length of the perpendicular from the point (2, -1, 4) on the straight line, 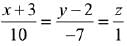 is: (2019)
is: (2019)
(1) greater than 3 but less than 4
(2) less than 2
(3) greater than 2 but less than 3
(4) greater than 4
Ans. (1)
Let P be the foot of perpendicular from point T (2, -1, 4) on the given line. So P can be assumed as P(10λ - 3, -7λ + 2, λ)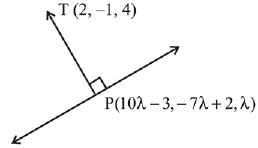
DR's of TP is proportional to 10λ - 5, - 7λ + 3, λ - 4
∵ TP and given line are perpendicular, so
10(10λ - 5) -7 (- 7λ + 3)+ 1(λ - 4) = 0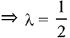
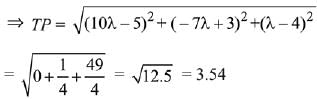
Hence, the length of perpendicular is greater than 3 but less than 4.
Q.45. The vector equation of the plane through the line of intersection of the planes x + y + z = 1 and 2x + 3y + 4z = 5 which is perpendicular to the plane x - y + z = 0 is: (2019)
(1) 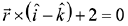
(2) 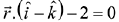
(3) 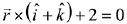
(4) 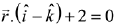
Ans. (4)
Equation of the plane passing through the line of intersection of x + y + z = 1 and 2x + 3y + 4z = 5 is (2x + 3y + 4z - 5) + λ (x + y + z - 1) = 0
∵ plane (i) is perpendicular to the plane x-y + z = 0
∴ (2 + λ)(1) + (3 + λ)(- 1) + (4 + λ)(1) = 0
2 + λ - 3 - λ + 4 + λ = 0
⇒ λ = -3
Hence, equation of required plane is -x + z- 2 = 0 or x - z + 2 = 0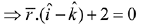
Q.46. If a point R(4, y, z) lies on the line segment joining the points P(2, -3, 4) and Q(8, 0, 10), then distance of R from the origin is: (2019)
(1) 2√14
(2) 2√21
(3) 6
(4) √53
Ans. (1)
Here, P, Q, R are collinear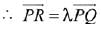
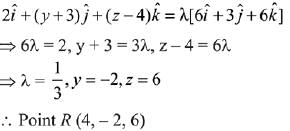
Now, or = 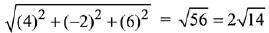
Q.47. If the line, 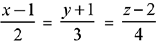 meets the plane, x + 2y + 3z = 15 at a point P, then the distance of P from the origin is: (2019)
meets the plane, x + 2y + 3z = 15 at a point P, then the distance of P from the origin is: (2019)
(1) √5 / 2
(2) 2 / √5
(3) 9/2
(4) 7/2
Ans. (3)
Let point on line be P (2k + 1, 3k - 1, 4k + 2)
Since, point P lies on the plane x + 2y + 3z = 15
∴ 2k + 1 + 6k - 2 + 12k + 6= 15
⇒ k = 1/2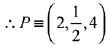
Then the distance of the point P from the origin is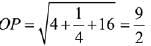
Q.48. A plane passing through the points (0, -1, 0) and (0, 0, 1) and making an angle π/4 with the plane y - z + 5 = 0, also passes through the point: (2019)
(1) (-√2, 1, -4)
(2) (-√2, -1, 4)
(3) (-√2, -1, -4)
(4) (√2, 1, 4)
Ans. (4)
Let the required plane passing through the points (0,-1, 0) and (0, 0, 1) be 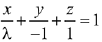 and the given plane is y - z + 5 = 0
and the given plane is y - z + 5 = 0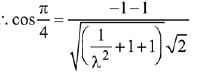
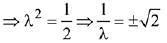
Then, the equation of plane is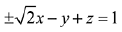
Then the point (√2, 1, 4) satisfies the equation of plane -√2x - y + z = 1
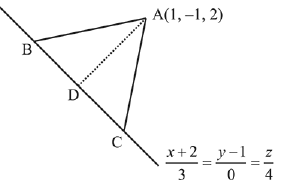
Q.49. The vertices B and C of a ΔABC lie on the line, 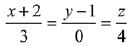 such that BC = 5 units. Then the area (in sq. units) of this triangle, given that the point A (1, -1, 2), is: (2019)
such that BC = 5 units. Then the area (in sq. units) of this triangle, given that the point A (1, -1, 2), is: (2019)
(1) 5√17
(2) 2√34
(3) 6
(4) √34
Ans. (4)
Let a point D on BC = (3λ - 2, 1, 4λ)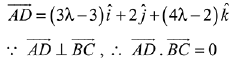
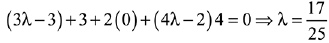
Hence, 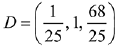
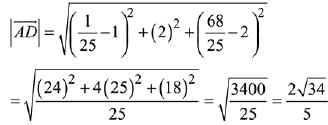
Area of triangle 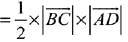
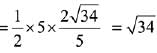
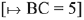
Q.50. Let P be the plane, which contains the line of intersection of the planes, x + y + z - 6 = 0 and 2x + 3y + z + 5 = 0 and it is perpendicular to the xy-plane. Then the distance of the point (0, 0, 256) from P is equal to: (2019)
(1) 17/√5
(2) 63√5
(3) 205√5
(4) 11/√5
Ans. (4)
Let the plane be
P = (2x + 3y + z + 5) + λ(x: +y + z- 6) = 0
∵ above plane is perpendicular to xy plane.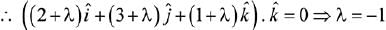
Hence, the equation of the plane is,
P = x + 2y+ 11 = 0
Distance of the plane P from (0, 0, 256)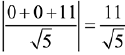
Q.51. If Q (0, -1, -3) is the image of the point P in the plane 3x - y + 4z = 2 and R is the point (3, -1, -2), then the area (in sq. units) of ΔPQR is: (2019)
(1) 2√13
(2) √91/4
(3) √91/2
(4) √65/2
Ans. (3)
Image of Q (0, -1, -3) in plane is,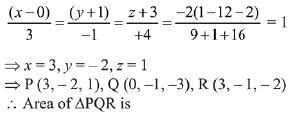
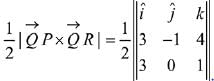
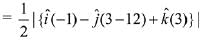
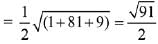
Q.52. Let A(3, 0, -1), B(2, 10, 6) and C (1, 2, 1) be the vertices of a triangle and M be the midpoint of AC. If G divides BM in the ratio, 2 : 1, then cos (∠GOA)(O being the origin) is equal to: (2019)
(1) 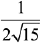
(2) 1/√15
(3) 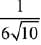
(4) 1/√30
Ans. (2)
G is the centroid of ΔABC.
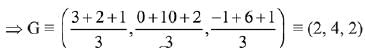

Q.53. If the length of the perpendicular from the point (β, 0, β) (β ≠ 0) to the line, 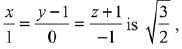 then β is equal to: (2019)
then β is equal to: (2019)
(1) 1
(2) 2
(3) -1
(4) -2
Ans. (3)
Given, 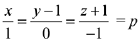 (let) and point P (β, 0, β)
(let) and point P (β, 0, β)
Any point on line A = (p, 1, -p -1)
Now, DR of AP ≡ <p - β, 1 - 0 - p - 1 - β>
Which is perpendicular to line.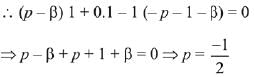
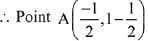
Given that distance AP 
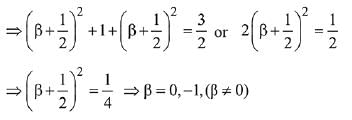
∴ β = -1
Q.54. A perpendicular is drawn from a point on the line 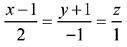 to the plane x + y + z = 3 such that the foot of the perpendicular Q also lies on the plane x - y + z = 3. Then the co-ordinates of Q are: (2019)
to the plane x + y + z = 3 such that the foot of the perpendicular Q also lies on the plane x - y + z = 3. Then the co-ordinates of Q are: (2019)
(1) (1, 0, 2)
(2) (2, 0, 1)
(3) (-1, 0, 4)
(4) (4, 0, -1)
Ans. (2)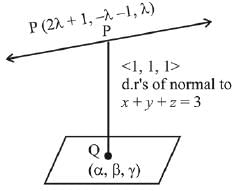
Let co-ordinates of Q be (α, β, γ), then
α + β + γ = 3 ...(i)
α - β + γ = 3 ...(ii)
⇒ α + γ = 3 and β = 0
Equating direction ratio's of PQ, we get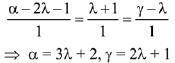
Substituting the values of a and y in equation (i), we get
⇒ 5λ + 3 = 3 ⇒ λ = 0
Hence, point is Q (2, 0, 1)
Q.55. If the plane 2x - y + 2z + 3 =0 has the distances 1/2 and 2/3 units from the planes 4x - 2y + 4z + λ = 0 and 2x - y + 2z + μ = 0, respectively, then the maximum value of λ + μ is equal to: (2019)
(1) 9
(2) 15
(3) 5
(4) 13
Ans. (4)
Let,
Given, distance between P1 and P2 is 1/3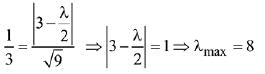
And distance between P1 and P3 is 2/3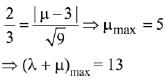
Q.56. If the line 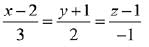 intersects the plane 2x + 3y - z + 13 = 0 at a point P and the plane 3x + y + 4z = 16 at a point Q, then PQ is equal to: (2019)
intersects the plane 2x + 3y - z + 13 = 0 at a point P and the plane 3x + y + 4z = 16 at a point Q, then PQ is equal to: (2019)
(1) 14
(2) √14
(3) 2√7
(4) 2√14
Ans. (4)
Let points P (3λ + 2, 2λ - 1, - λ + 1) and Q(3μ + 2, 2μ - 1, - μ + 1)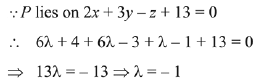
Hence, P (- 1, -3, 2)
Similarly, Q lies on 3x + y + 4z = 16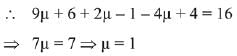
Hence, Q is (5, 1, 0)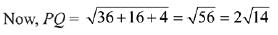
Q.57. A plane which bisects the angle between the two given planes 2x - y + 2z -4 = 0 and x + 2y + 2z - 2 = 0, passes through the point: (2019)
(1) (-1, -4, 1)
(2) (1, 4, -1)
(3) (2, 4, 1)
(4) (2, -4, 1)
Ans. (4)
The equations of angle bisectors are,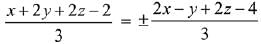
⇒ x - 3y - 2 = 0
or 3x + y + 4z - 6 = 0
(2, -4, 1) lies on the second plane.
Q.58. The length of the perpendicular drawn from the point (2, 1,4) to the plane containing the lines 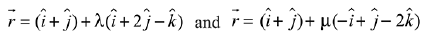 is: (2019)
is: (2019)
(1) 3
(2) 1/3
(3) √3
(4) 1/√3
Ans. (3)
The equation of plane containing two given lines is,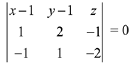
On expanding, we get x - y - z = 0
Now, the length of perpendicular from (2, 1, 4) to this plane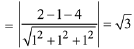
Q.59. Let 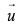 be a vector coplanar with the vectors
be a vector coplanar with the vectors 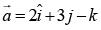 and
and 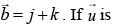 perpendicular to
perpendicular to 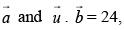 then,
then, 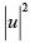 is equal to: (2018)
is equal to: (2018)
(1) 336
(2) 315
(3) 256
(4) 84
Ans. (1)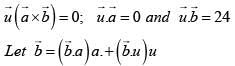

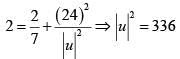
Q.60. If L1 is the line of intersect ion of the planes 2x - 2y + 3z = 0, x - y + z = 0 and L2 is the line of intersection of the planes x + 2y - z - 3 = 0, 3x - y + 2z = 0 then the distance of the origin fro m the plane, containing the lane L1 and L2 , is: (2018)
(1) 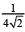
(2) 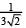
(3) 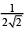
(4) 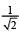
Ans. (2)
Vectors along the given lines L1, L2 are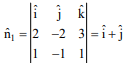
and 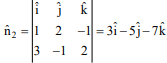
Putting y = 0 in 1st two equation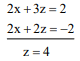
Point on the plane is (–5, 0, 4) and normal vector of required plane is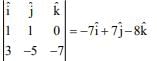
Hence, equation of plane is - 7x + 7y - 8z - 3 = 0
Perpendicular distance is 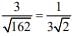
Q.61. The length of the project ion of the line segment joining the points (5, -1, 4) and (4, -1, 3) on the plane, x + y + z = 7 is: (2018)
(1) 2/√3
(2) 2/3
(3) 1/3
(4) 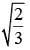
Ans. (4)
D.R’s of AB = (1, 0, 1)
D.R’s of normal to plane = (1, 1, 1)
AB = √2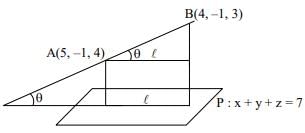
Length of projection = 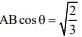
Q.62. Let 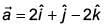 and
and 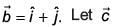 be a vector such that
be a vector such that 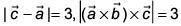 and the angle between
and the angle between  be 30°. Then
be 30°. Then 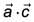 is equal to (2017)
is equal to (2017)
(1) 1/8
(2) 25/8
(3) 2
(4) 5
Ans. (3)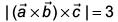
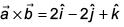
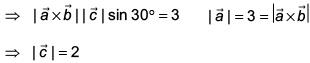
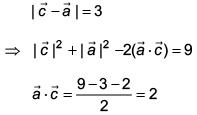
Q.63. If the image of the point P(1, –2, 3) in the plane, 2x + 3y – 4z + 22 = 0 measured parallel to the line, x/1 = y/4 = z/5 is Q, then PQ is equal to (2017)
(1) 6√5
(2) 3√5
(3) 2√42
(4) √42
Ans. (3)
Equation of PQ,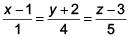
Let M be (λ+1, 4λ- 2, 5λ+ 3)
As it lies on 2x + 3y – 4z + 22 = 0
λ = 1
For Q, λ = 2
Distance PQ
= 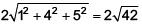
Q.64. The distance of the point (1, 3, –7) from the plane passing through the point (1, –1, –1), having normal perpendicular to both the lines 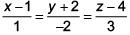 and
and 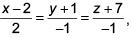 is (2017)
is (2017)
(1) 10/√74
(2) 20/√74
(3) 10/√83
(4) 5/√83
Ans. (3)
Let the plane be
a(x - 1)+ b( y + 1) + c(z +1) = 0
It is perpendicular to the given lines
a – 2b + 3c = 0
Solving, a : b : c = 5 : 7 : 3
∴ The plane is 5x + 7y + 3z + 5 = 0
Distance of (1, 3, –7) from this plane = 10/√83
Q.65. The coodinates of the foot of the perpendicular from the point (1, -2,1) on the plane containing the lines, 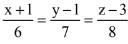 and
and 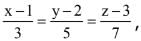 is: (2017)
is: (2017)
(1) (2, -4, 2)
(2) (1, 1, 1)
(3) (0, 0, 0)
(4) (-1, 2, -`= 1)
Ans. (3)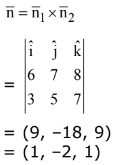
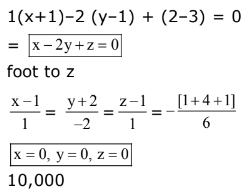
Q.66. The line of intersection of the planes 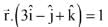 and
and 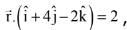 is: (2017)
is: (2017)
(1) 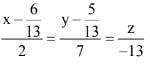
(2) 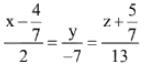
(3) 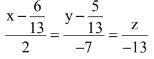
(4) 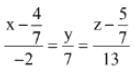
Ans. (3)
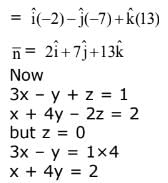
13 x = 6
x = 6/13y
y = 5/13
.... is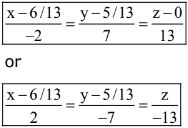
Q.67. The area (in sq. units) of the parallelogram whosed diagonals are along the vectors 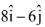 and
and 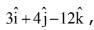 is: (2017)
is: (2017)
(1) 20
(2) 65
(3) 52
(4) 26
Ans. (2)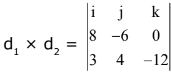
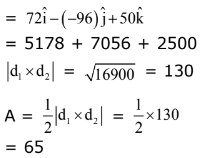
Q.68. If the line, 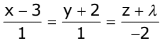 lies in the plane, 2x - 4y + 3z = 2, then the shortest distance between this line and the line,
lies in the plane, 2x - 4y + 3z = 2, then the shortest distance between this line and the line, 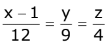 is: (2017)
is: (2017)
(1) 1
(2) 2
(3) 3
(4) 0
Ans. (4)
pt (3, -2, λ) on pline 2x - 4y +3z - 2 = 0
= 6 + 8 - 3λ - 2 = 0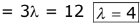
Now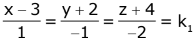 ...(1)
...(1)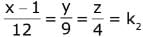 ...(2)
...(2)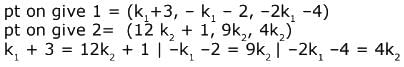
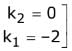
p (1, 0, 0)
gives are ditersech - thortest distance = 0
Q.69. If x = a, y = b, z = c is a solution of the system of linear equations
x + 8y + 7z = 0
9x + 2y +3z = 0
y + y + z = 0
such that the point (a, b, c) lies on the plane x + 2y + z = 6, then 2a + b + c equals: (2017)
(1) 2
(2) -1
(3) 1
(4) 0
Ans. (1)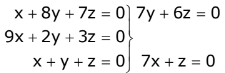
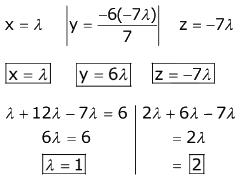
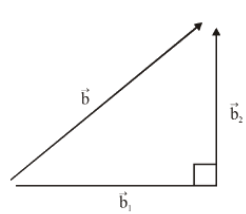
Q.70. If the vector 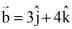 is written as the sum of a vector
is written as the sum of a vector 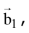 parallel to
parallel to 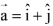 and a vector
and a vector 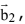 perpendicular to
perpendicular to  is equal to: (2017)
is equal to: (2017)
(1) 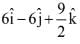
(2) 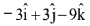
(3)
(4)
Ans. (1)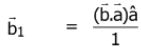
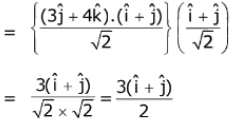
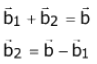
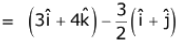
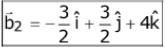
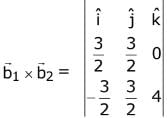
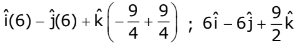
Q.71. If a variable plane, at a distance of 3 units from the origin, intersects the coordinate axes at A, B and C, then the locus of the centroid of ΔABC is. (2017)
(1) 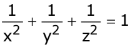
(2) 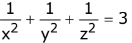
(3) 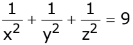
(4) 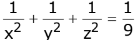
Ans. (1)
Let Centroid be (h, k, l)
∴ x - intp = 3h Y - intp = 3k, 3 - int = 3l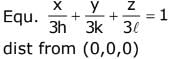

Q.72. The distance of the point (1, -5, 9) from the plane x - y + z = 5 measured along the line x = y = z is: (2016)
(1) 3√10
(2) 10√3
(3) 10/√3
(4) 20/3
Ans. (2)
Let Q(1, -5, 9)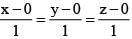
Line is 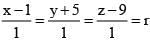 (say)
(say)
Any pt on line we can take P(r + 1, r - 5, r + 9)
So, Pt satisfy Plane
=>(r + 1) - (r - 5) + (r + 9) = 5 r = -10 So, Point P = (-9, -15, -1)
Distance is PQ = 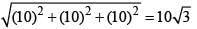
Q.73. If the line, 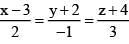 lies in the plane, lx + my - z = 9, then l2 + m2 is equal to: (2016)
lies in the plane, lx + my - z = 9, then l2 + m2 is equal to: (2016)
(1) 26
(2) 18
(3) 5
(4) 24
Ans. (4)
Point on line is P = (3, -2, -4)
'P’ lies on lx + my - z = 9
=> 3l - 2m + 4 = 9
3l - 2m = 5 ....(1)
As line lies on plane
=> 2 x l + m x (-1) + 3 x (-1) = 0
2l - m = 3 .....(3)
Solving l = 1, m = -1
So, l2 + m2 = 2
Q.74. Let 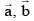 and
and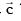 be three unit vectors such that
be three unit vectors such that 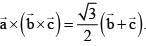 If
If 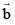 is not parallel to c , then the angle between
is not parallel to c , then the angle between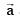 and
and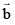 is: (2016)
is: (2016)
(1) 3π/4
(2) π/2
(3) 2π/3
(4) 5π/6
Ans. (4)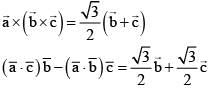
Equate,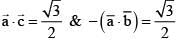
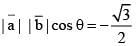
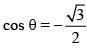 as
as 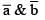 unit vectors
unit vectors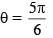
Q.75. The shortest distance between the lines 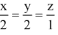 and
and 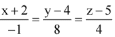 lies in the interval: (2016)
lies in the interval: (2016)
(1) (2, 3]
(2) [0, 1)
(3) (3, 4]
(4) [1, 2)
Ans. (1)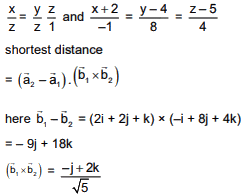
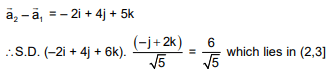
Q.76. The distance of the point (1, -2, 4) from the plane passing through the point (1, 2, 2) and perpendicular to the planes x - y + 2z = 3 and 2x - 2y + z + 12 = 0, is (2016)
(1) 1/√2
(2) 2
(3) √2
(4) 2√2
Ans. (4)
Equation of plane ⊥ to the planes.
x - y + 2z = 3 & 2x - 2y + z + 12 = 0
and passes through (1, 2, 2) is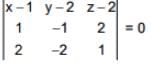
3(x - 1) + 3(y - 2) = 0
x + y = 3 ..... (1)
distance of plane x + y - 3 = 0 from (1, - 2, 4) is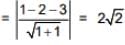
Q.77. In a triangle ABC, right angled at the vertex A, if the position vectors of A, B and C are respectively 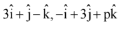 and
and 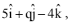 then the point (p, q) lies on a line (2016)
then the point (p, q) lies on a line (2016)
(1) parallel to y-axis
(2) making an acute angle with the positive direction of x-axis
(3) parallel to x-axis
(4) making an obtuse angle with the position direction of x-axis.
Ans. (2)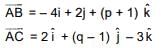
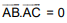 ⇒ - 8 + 2(9 - 1) - 3 (p + 1) = 0 ⇒ - 3p + 2q - 13 = 0
⇒ - 8 + 2(9 - 1) - 3 (p + 1) = 0 ⇒ - 3p + 2q - 13 = 0
⇒ (p, q) lies on line
3x - 2y + 13 = 0
slope = 3/2
Q.78. ABC is a triangle in a plane with vertices A(2, 3, 5), B(-1, 3, 2) and C(λ, 5, µ). If the median through A is equally inclined to the coordinate axes, then the value of (λ3 + µ3 + 5) is (2016)
(1) 676
(2) 1130
(3) 1348
(4) 1077
Ans. (3)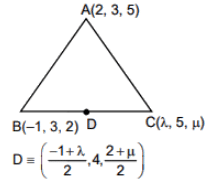
direction cosine of AD = 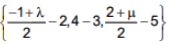
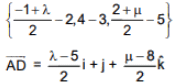
⇒ 
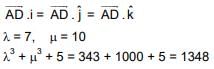
Q.79. Let ABC be a triangle whose circumcentre is at P. If the position vectors of A, B, C and P are 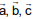 and
and 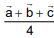 respectively, then the position vector of the orthocentre of this triangle, is (2016)
respectively, then the position vector of the orthocentre of this triangle, is (2016)
(1) 
(2) 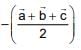
(3) 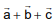
(4) 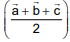
Ans. (4)
Position vector of the centroid of 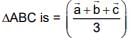
Now we known that centroid divides the line joining orthocentre to circum centre divided by centriod divided by centroid in the ratio in 2 : 1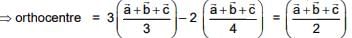
Q.80. The number of distinct real values of λ for which the lines  are coplanar is (2016)
are coplanar is (2016)
(1) 3
(2) 2
(3) 1
(4) 4
Ans. (1)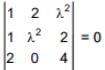
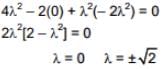
|
276 videos|265 docs|221 tests
|

















