JEE Main Previous Year Questions (2016- 2024): Heat & Thermodynamics- 2 | Physics for Airmen Group X - Airforce X Y / Indian Navy SSR PDF Download
Q.43. One mole of an ideal monatomic gas is compressed isothermally in a rigid vessel to double its pressure at room temperature, 27°C. The work done on the gas will be: (2018)
(1) 300 R ln 7
(2) 300 R ln 6
(3) 300 R ln 2
(4) 300 R
Ans. (3)
Solution.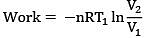
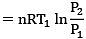
= 300R ln 2
Q.44. A Carnot's engine works as a refrigerator between 250 K and 300 K. It receives 500 cal heat from the reservoir at the lower temperature. The amount of work done in each cycle to operate the refrigerator is: (2018)
(1) 772 J
(2) 2520 J
(3) 2100 J
(4) 420 J
Ans. (4)
Solution.
Given,
Q2 = 500 cal.
ηCarnot = 1 - T2/T1
= 1/6
and (COP)HP = 1/ηCarnot = 6
(Cop)HP − (Cop)Ref = 1
So, (cop)Ref = 5 = Q2/w
so w = 100 cal
Or w = 420 J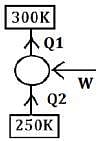
Q.45. Two moles of helium are mixed with an moles of hydrogen. If Cp/Cv = 3/2 for the mixture then the value of n is
(1) 1
(2) 3
(3) 2
(4) 3/2
Ans. (3)
Solution.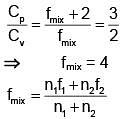
⇒ 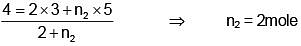
Q.46. A heating element has a resistance of 100Ω at room temperature. When it is connected to a supply of 220V a steady current of 2A passes in it and temperature is 500°C more than room temperature. What is the temperature coefficient of resistance of the heating element? (2018)
(1) 5 × 10-4 °C-1
(2) 2 × 10-4 °C-1
(3) 1 × 10-4 °C-1
(4) 0.5 × 10-4 °C-1
Ans. (2)
Solution.
Resistance after temperature increases by 500°C = 220/2 = 110Ω
110 = 100 (1 + α500)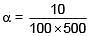
a = 2 × 10-4 °C-1
Q.47. One mole of an ideal monatomic gas is taken along the path ABCA as shown in the PV diagram. The maximum temperature attained by the gas along the path BC is given by :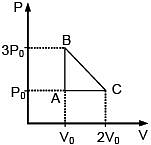
(1) 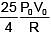
(2) 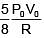
(3) 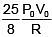
(4) 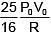
Ans. (3)
Solution.
Equation of line BC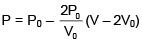
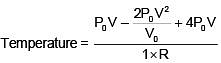
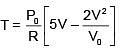
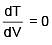
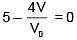
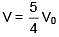
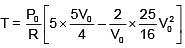
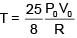
Q.48. A copper ball of mass 100 gm is at a temperature T. It is dropped in a copper calorimeter of mass 100 gm, filled with 170 gm of water at room temperature. Subsequently, the temperature of the system is found to be 75°C. T is given by :
(Given : room temperature = 30°C, specific heat of copper = 0.1 cal/gm°C) (2017)
(1) 1250°C
(2) 825°C
(3) 800°C
(4) 885°C
Ans. D
Solution.
100 × 0.1 × (t – 75) = 100 × 0.1 × 45 + 170 × 1 × 45
10t – 750 = 450 + 7650
10t = 1200 + 7650
10t = 8850
t = 885°C
Q.49. An external pressure P is applied on a cube at 0°C so that it is equally compressed from all sides. K is the bulk modulus of the material of the cube and a is its coefficient of linear expansion. Suppose we want to bring the cube to its original size by heating. The temperature should be raised by: (2017)
(1) 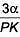
(2) 3PKα
(3) 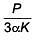
(4) 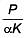
Ans. C
Solution.
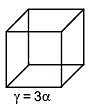
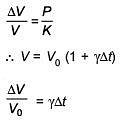
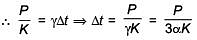
Q.50. The temperature of an open room of volume 30 m3 increases from 17°C to 27°C due to the sunshine. The atmospheric pressure in the room remains 1 × 105 Pa. If ni and nf are the number of molecules in the room before and after heating, then nf – ni will be (2017)
(1) 2.5 × 1025
(2) –2.5 × 1025
(3) –1.61 × 1023
(4) 1.38 × 1023
Ans. (2)
Solution.
n1 = initial number of moles;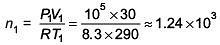
n2 = final number of moles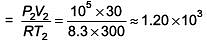
Change of number of molecules
nf – ni = (n2 – n1) × 6.023 × 1023
≈ – 2.5 × 1025
Q.51. Cp and Cv are specific heats at constant pressure and constant volume respectively. It is observed that
Cp – Cv = a for hydrogen gas
Cp – Cv = b for nitrogen gas
The correct relation between a and b is: (2017)
(1) a = 14b
(2) a = 28b
(3) 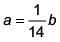
(4) a = b
Ans. (1)
Solution.
Let molar heat capacity at constant pressure = Xp and molar heat capacity at constant volume = Xv
Xp – Xv =R
MCp – MCv = R
Cp – Cv = R/M
For hydrogen; a = R/2
For N2; b = R/28
a/b = 14
a = 14b
Q.52. In an experiment a sphere of aluminium of mass 0.20 kg is heated upto 150°C. Immediately, it is put into water of volume 150 cc at 27°C kept in a calorimeter of water equivalent to 0.025 kg. Final temperature of the system is 40°C. The specific heat of aluminium is -(take 4.2 Joule = 1 calorie)
(1) 434J/kg-°C
(2) 378J/kg-°C
(3) 315J/kg-°C
(4) 476J/kg-°C
Ans. (1)
Solution.
Q given = Q used
0.2 × S× (150 – 40) = 150 × 1 × (40 – 27) + 25 × (40 – 27)
0.2 × S × 110 = 150 × 13 + 25 × 13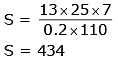
Q.53. An engine operates by taking n moles of an ideal gas through the cycle ABCDA shown in figure. The thermal efficiency of the engine is - (Take Cv = 1.5 R, where R is gas constant)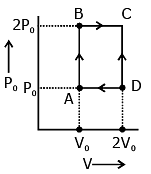
(1) 0.24
(2) 0.15
(3) 0.32
(4) 0.08
Ans. (2)
Solution.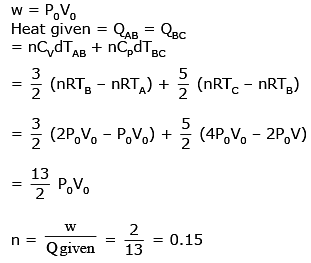
Q.54. An ideal gas has molecules with 5 degrees of freedom. The ratio of specific heats at constant pressure (CP) and at constant volume (CV) is
(1) 7/5
(2) 6
(3) 7/2
(4) 5/2
Ans. (1)
Solution.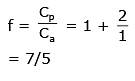
Q.55. A steel rail of length 5 m and area of cross section 40 cm2 is prevented from expanding along its length while the temperature rises by 10°C. If coefficient of linear expansion and Young's modulus of steel are 1.2 × 10-5 K-1 and 2 × 1011 Nm-2 respectively, the force developed in the rail is approximately : (2017)
(1) 2 × 107 N
(2) 2 × 109 N
(3) 3 × 10-5 N
(4) 1 × 105 N
Ans. 4
Solution.
F = yA ∝ Dt
= 2 × 1011 × 40 × 10-4 × 1.2 × 10-5 × 10
= 9.6 × 104 = 1 × 105 N
Q.56. Imagine that a reactor converts all given mass into energy and that it operates at a power level of 109 watt. The mass of the fuel consumed per hour in the reactor will be : (velocity of light, c is 3 × 108 m/s) (2017)
(1) 6.6 × 10–5 gm
(2) 0.96 gm
(3) 4 × 10–2 gm
(4) 0.8 gm
Ans. (3)
Solution.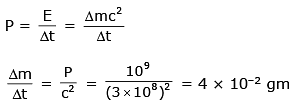
Q.57. In a physical balance working on the principle of moments, when 5 mg weight is placed on the left pan, the beam becomes horizontal. Both the empty pans of the balance are of equal mass. Which of the following statements is correct ?
(1) Every object that is weighted using this balance appears lighter than its actual weight
(2) Left arm is shorter than the right arm
(3) Both the arms are of same length
(4) Left arm is longer than the right arm
Ans. (2)
Q.58. A potentiometer PQ is set up to compare two resistances as shown in the figure. The ammeter A in the circuit reads 1.0 A when two way key K3 is open. The balance point is at a length l1 cm from P when two way key K3 is plugged in between 2 and 1, while the balance point is at a length l2 cm from P when key K3 is plugged in between 3 and 1. The ratio of the two resistance R1/R2 is found to be -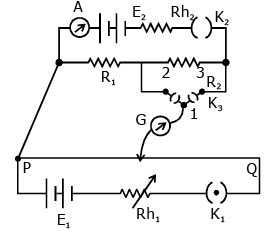
Ans. (1)
Solution.
When key is at point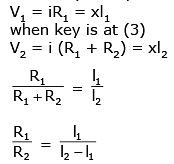
Q.59. A pendulum clock loses 12 s a day if the temperature is 40°C and gains 4s a day if the temperature is 20°C. The temperature at which the clock will show correct time, and the co-efficient of linear expansion (α) of the metal of the pendulum shaft are respectively: (2016)
(1) 25°C; α = 1.85 x 10-5/°C
(2) 60°C; α = 1.85 x 10-4/°C
(3) 30°C; α = 1.85 x 10-3/°C
(4) 55°C; α = 1.85 x 10-2/°C
Ans. (1)
Solution.
Time period of pendulum,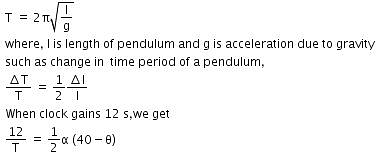
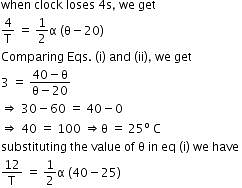
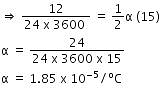
Thus, the coefficient of linear expansion in pendulum clock = 1.85 x 10-5/C
Q.60. An ideal gas undergoes a quasi static, reversible process in which its molar heat capacity Cremains constant. If during this process the relation of pressure P and volume V is given by PVn = constant, then n is given by (Here CP and CV are molar specific heat at constant pressure and constant volume, respectively): (2016)
(1) 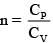
(2) 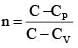
(3) 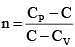
(4) 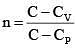
Ans (2)
Solution: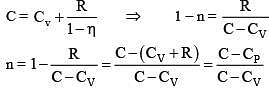
Q.61. ‘n’ moles of an ideal gas undergoes a process A → B as shown in the figure. The maximum temperature of the gas during the process will be: (2016)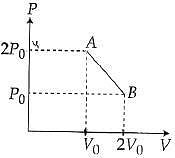
(1) 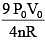
(2) 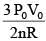
(3) 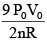
(4) 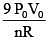
Ans. (1)
Solution.
Equation of line AB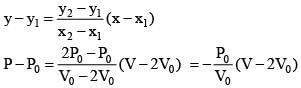
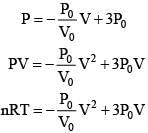
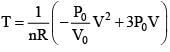
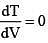
(For maximum temperature)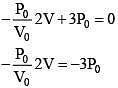
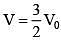
(Condition for maximum temperature)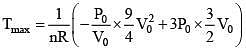
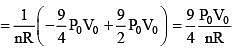
Q.62. The temperature dependence of resistances of Cu and undoped Si in the temperature range 300-400 K, is best described by:
(1) Linear increase for Cu, linear increase for Si
(2) Liner increase for Cu, exponential increase for Si
(3) Linear increase for Cu, exponential decrease for Si
(4) Linear decrease for Cu, linear decrease for Si (2016)
Ans. (3)
Solution.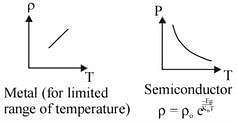
Q.63. 200 g water is heated from 40°C to 60°C. Ignoring the slight expansion of water, the change in its internal energy is closed to (Given specific heat of water = 4184 J/kg/K): (2016)
(1) 16.7 kJ
(2) 167.4kJ
(3) 4.2 kJ
(4) 8.4 kJ
Ans. (1)
Solution.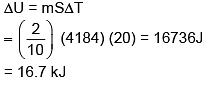
Q.64. A simple pendulum made of a bob of mass m and a metallic wire of negligible mass has time period 2s at T = 0°C. If the temperature of the wire is increased and the corresponding charge in its time period is plotted against its temperature, the resulting graph is a line of slop S. If the coefficient of linear expansion of metal is a then the value of S is: (2016)
(1) 1/α
(2) 2α
(3) α/2
(4) α
Ans. (4)
Solution.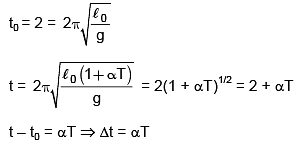
Q.65. A carnot freezer takes heat from water at 0°C inside it and rejects it to the room at a temperature of 27°C. The latent heat of ice is 336 × 103 J kg–1. If 5 kg of water at 0°C is converted into ice at 0°C by the freezer, then the energy consumed by the freezer is close to:
(1) 1.68 × 106 J
(2) 1.71 × 107 J
(3) 1.51 × 105 J
(4) 1.67 × 105 J
Ans. (4)
Solution.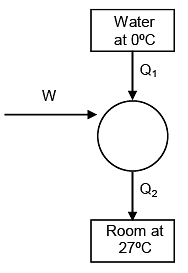
heat required to freeze 5 kg water
= 5 × 336 × 103
= 1680 × 103 Joule
⇒ Q1 = 1680 KJ
for carnot's cycle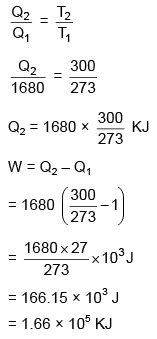
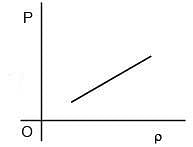
Q.66. Which of the following shown the correct relationship between the pressure 'P' and density r of an ideal gas at constant temperature ?
(1)
(2)
(3)
(4)
Ans. (1)
Solution.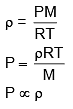
|
199 videos|422 docs|281 tests
|


















