NCERT Exemplar: Motion in a Straight Line - 2 | NCERT Exemplar & Revision Notes for NEET PDF Download
SHORT ANSWER TYPE QUESTIONS
Q.1. A ball is dropped and its displacement vs time graph is as shown Fig. (displacement x is from ground and all quantities are +ve upwards).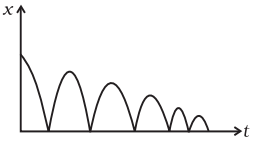 (a) Plot qualitatively velocity vs time graph.
(a) Plot qualitatively velocity vs time graph.
(b) Plot qualitatively acceleration vs time graph.
Ans. Key concept: To calculate velocity we will find slope which is calculated by dx/dt for displacement-time curve and to find acceleration we will find slope dv/dt of velocity-time curve.
Sign convention: We are taking downward as negative and upward as positive.
Ball is bouncing on the ground and it is clear from the graph that displacement x is positive throughout. Ball is dropped from a height and its velocity increases in downward direction due to gravity pull. In this condition v is negative but acceleration of the ball is equal to acceleration due to gravity i.e., a = -g. When ball rebounds in upward direction its velocity is positive but acceleration is a = -g.
(a) The velocity-time graph of the ball is shown in fig. (i).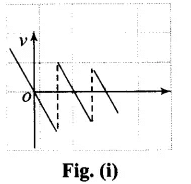 (b) The acceleration-time graph of the ball is shown in fig. (ii).
(b) The acceleration-time graph of the ball is shown in fig. (ii).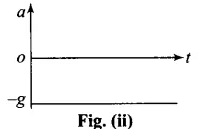
Q.2. A particle executes the motion described by x(t) = x0(1 - e-γt); t ≥ 0, x0 > 0.
(a) Where does the particle start and with what velocity?
(b) Find maximum and minimum values of x (t), v (t), a (t). Show that x (t) and a (t) increase with time and v (t) decreases with time.
Ans. Initially, we have to calculate velocity and acceleration and then we can determine the maximum or minimum value accordingly.
We have displacement as a function of time,
x(t) = x0(1 - e-γt)
By differentiating this equation w.r.t. time we get velocity of the particle as a function of time.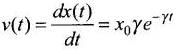
If we again differentiate this equation w.r.t. time we will get acceleration of the particle as a function of time.
(a) When t = 0; x(t) = x0(1 - e-0) = x0(1 - 1) = 0
x(t = 0) = x0 γe-0 = x0γ(1) = γxo
(b) x(t) is maximum when t = ∞[x(t)]max = x0 
Q.3. A bird is tossing (flying to and fro) between two cars moving towards each other on a straight road. One car has a speed of 18 m/h while the other has the speed of 27km/h. The bird starts moving from first car towards the other and is moving with the speed of 36km/h and when the two cars were separted by 36 km. What is the total distance covered by the bird? What is the total displacement of the bird?
Ans. Concept of relative velocity (for 1-D): If two objects are moving along the same straight line and we are observing the motion from the frame of one object. Then for the relative velocity, it will be subtracted for velocities in same direction and added for velocities in opposite directions. (Remember: add or subtract them with proper sign conventions).
In this problem we have to use the concept of relative velocity. According to the problem, Speed of first car = 18 km/h
According to the problem, Speed of first car = 18 km/h
Speed of second car = 27 km/h
∴ Relative speed of each car w.r.t. each other
= 18 + 27 = 45 km/h
Distance between the cars = 36 km
∴ Time of meeting the cars (t)
Speed of the bird (vb) = 36 km/h
Distance covered by the bird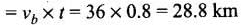
Q.4. A man runs across the roof-top of a tall building and jumps horizontally with the hope of landing on the roof of the next building which is of a lower height than the first. If his speed is 9 m/s, the (horizontal) distance between the two buildings is 10 m and the height difference is 9 m, will he be able to land on the next building ? (take g = 10 m/s2)
Ans. Key concept: Horizontal Projectile:
When a body is projected horizontally from a certain height ‘y’ vertically above the ground with initial velocity u. If friction is considered to be absent, then there is no other horizontal force which can affect the horizontal motion. The horizontal velocity therefore remains constant and so the object covers equal distance in horizontal direction in equal intervals of time.
Time of flight: If a body is projected horizontally from a height h with velocity u and time taken by the body to reach the ground is T, then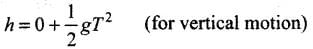
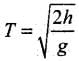
Horizontal range: Let R be the horizontal distance travelled by the body
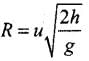
We will apply kinematic one by one along downward and along horizontal. We first consider motion along horizontal and there is no horizontal force which can affect the horizontal motion. The horizontal velocity therefore remains constant and so the object covers equal distance in horizontal direction in equal intervals of time.
According the problem, horizontal speed of the man (u x) = 9 m/s Horizontal distance between the two buildings = 10 m
Height difference between the two buildings = 9 m and g =10 m/s2
Let the man jumps from point A and land on the roof of the next building at point B.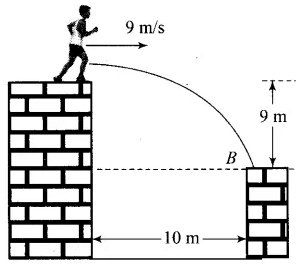 Taking motion in vertical direction,
Taking motion in vertical direction,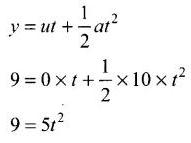
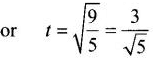
∴ Horizontal distance travelled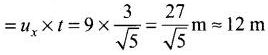
Horizontal distance travelled by the man is greater than 10 m, therefore, he will land on the next building.
Q.5. A ball is dropped from a building of height 45 m. Simultaneously another ball is thrown up with a speed 40 m/s. Calculate the relative speed of the balls as a function of time.
Ans. In motion under gravity, if the ball is released or dropped that means its initial velocity is zero. In this problem as ball is dropped, so its initial velocity will be taken as zero. We will apply kinematic equations.
According to the problem, for the ball dropped from the building, u1 = 0, u2 = 40 m/s
Velocity of the ball after time t,
v1 = u1 - gt
v1 = -gt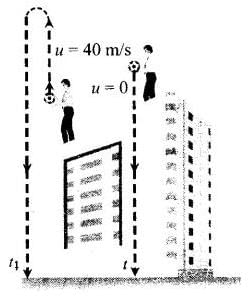 And for another ball which is thrown upward, u2 = 40 m/s
And for another ball which is thrown upward, u2 = 40 m/s
Velocity of the ball after time t,
v2 = u2 - gt = (40 - gt)
∴ Relative velocity of one ball w.r.t. another ball is
v12 = v1 - v2 = - gt - [-40 -gt]
v12 = v1 - v2 = - gt + 40 + gt = 40 m/s
Important point: Sign Convention:
Any vector quantity directed upward will be taken as positive and directed downward will be taken as negative. According to this sign convention: (i) Displacement will be taken as positive if final position lies above initial position and negative if final position lies below initial position.
(i) Displacement will be taken as positive if final position lies above initial position and negative if final position lies below initial position.
(ii) Velocity(initial or final) will be taken as positive if it is upward and negative if it is downward.
(iii) Acceleration a is always taken to be -g.
In equations of motions we replace a by -g (minus sign, because acceleration is always directed downward)
Q.6. The velocity-displacement graph of a particle is shown in Fig.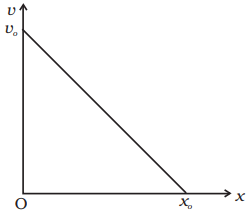
(a) Write the relation between v and x.
(b) Obtain the relation between acceleration and displacement and plot it.
Ans. In this problem, we will use equation of straight line graph (linear equation), y = mx + c.
In this equation, m is the slope of the graph and c is the interception on y-axis.
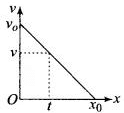 Now according to the problem, initial velocity = v0
Now according to the problem, initial velocity = v0
Let the distance travelled in time t = x0.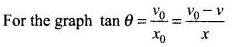 ....(i)
....(i)
where, v is velocity and x is displacement at any instant of time t.
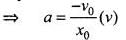
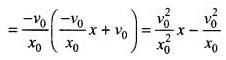
Graph of a versus x is given below.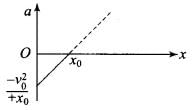
LONG ANSWER TYPE QUESTIONS
Q.1. It is a common observation that rain clouds can be at about a kilometre altitude above the ground.
(a) If a rain drop falls from such a height freely under gravity, what will be its speed? Also calculate in km/h. (g = 10m/s2)
(b) A typical rain drop is about 4mm diameter. Momentum is mass x speed in magnitude. Estimate its momentum when it hits ground.
(c) Estimate the time required to flatten the drop.
(d) Rate of change of momentum is force. Estimate how much force such a drop would exert on you.
(e) Estimate the order of magnitude force on umbrella. Typical lateral separation between two rain drops is 5 cm.
(Assume that umbrella is circular and has a diameter of 1m and cloth is not pierced through !!)
Ans. Key concept: This problem can be solved by kinematic equations of motion and Newton’s second law that Fext = dp/dt will be used, where dp is change in momentum over time dt.
(a) According to the problem (h) = 1 km = 1000 m and we know that the initial velocity of the ball is zero. And displacement covered by rain drop in downward direction, so we will taking h as negative. (We are neglecting the air resistance.)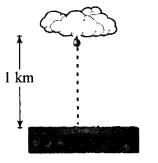 Velocity attained by the rain drop in freely falling through a height h is
Velocity attained by the rain drop in freely falling through a height h is
v2 = u2 - 2g(-h)
As u = 0
So,
(b) Diameter of the drop (d) = 2r = 4 mm
Radius of the drop (r) = 2 mm = 2 x 10-3 m
Mass of a rain drop (w) = V x ρ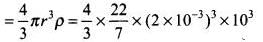
(∵ Density of water = 103 kg/m3)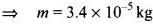
Momentum of the rain drop (p) = mv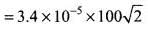
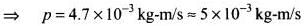
(c) Time required to flatten the drop = Time taken by the drop to travel the distance equal to the diameter of the drop near the ground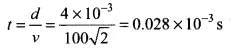

(d) Force exerted by a rain drop is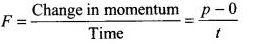
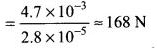
(e) Radius of the umbrella (R) = 1/2 m
∴ Area of the umbrella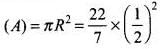
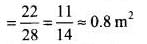
Number of drops striking the umbrella simultaneously with average separation of 5 cm (5 x 102 m)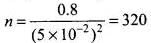
∴ Net force exerted on umbrella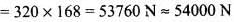
Q.2. A motor car moving at a speed of 72km/h can not come to a stop in less than 3.0 s while for a truck this time interval is 5.0 s. On a highway the car is behind the truck both moving at 72km/h. The truck gives a signal that it is going to stop at emergency. At what distance the car should be from the truck so that it does not bump onto (collide with) the truck. Human response time is 0.5s.
Ans. According to the problem, speed of car as well as truck = 72 km/h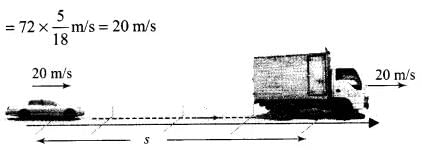
Time required to stop the truck = 5 s
Finally the truck comes to rest, so Final velocity of truck will be zero.
Retardation produced by truck: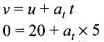
or at = -4 m/s2
Time required to stop the car = 3 s
Finally the car comes to rest just behind the truck in the same time to avoid collision, so final velocity of car will also be zero.
Retardation produced by car is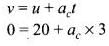
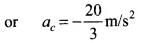
Let car be at a distance s from the truck, when truck gives the signal and t be the time taken to cover this distance.
As human response time is 0.5 s, in this time car will cover some distance with uniform velocity. Therefore, time of retarded motion of car is (t - 0.5) s. Velocity of car after time t,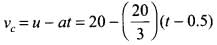
Velocity of truck after time r,
vt = 20 - 4t
To avoid the car bump onto the truck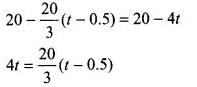
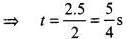
Distance travelled by the truck in time t,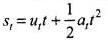
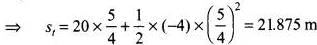
Distance travelled by car in time t = Distance travelled by car in 0.5 s (without retardation) + Distance travelled by car in (t - 0.5) s (with retardation)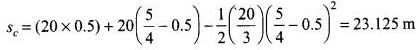
∴ sc - st = 23.125 - 21.875 = 1.250 m
Therefore, to avoid the collision with the truck, the car must maintain a distance from the truck more than 1.250 m.
Q.3. A monkey climbs up a slippery pole for 3 seconds and subsequently slips for 3 seconds. Its velocity at time t is given by v(t) = 2t (3 - t); 0< t < 3 and v (t)=– (t – 3)(6 – t) for 3 < t < 6 s in m/s. It repeats this cycle till it reaches the height of 20 m.
(a) At what time is its velocity maximum?
(b) At what time is its average velocity maximum?
(c) At what time is its acceleration maximum in magnitude?
(d) How many cycles (counting fractions) are required to reach the top?
Ans. We have to calculate time corresponding to maximum velocity. So we first need to find the maximum velocity in this problem. To calculate maximum dv velocity we will use dv/dt = 0
Given
v(t) = 2t(3 - t) = 6t - 2t2 ....(i)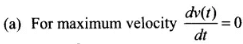
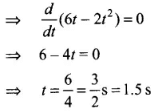
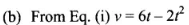
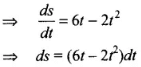
where, s is displacement
∴ Distance travelled in time interval 0 to 3 s,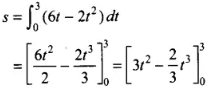
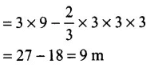
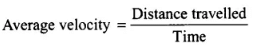
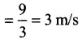
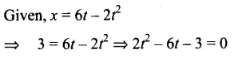
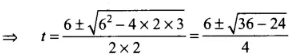
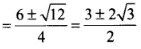
Considering positive sign only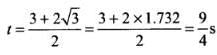
(c) In a periodic motion when Velocity is zero acceleration will be maximum putting v = 0 in Eq. (i).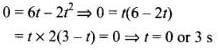
(d) Distance covered in 0 to 3 s = 9 m
Distance covered in 3 to 6 s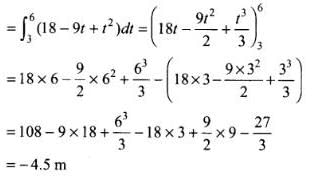
∴ Total distance travelled in one cycle
= s1 + s2 = 9 - 4.5 = 4.5 m
Number of cycles to be covered in total distance = 20/4.5 ≈ 4.44 ≈ 5
Q.4. A man is standing on top of a building 100 m high. He throws two balls vertically, one at t = 0 and other after a time interval (less than 2 seconds). The later ball is thrown at a velocity of half the first. The vertical gap between first and second ball is +15 m at t = 2 s. The gap is found to remain constant. Calculate the velocity with which the balls were thrown and the exact time interval between their throw.
Ans. We solve this problem by using kinematic equations with proper sign convention and to calculate time interval we will take We solve this problem by using kinematic equations with proper sign convention and to calculate time interval we will take difference of displacements.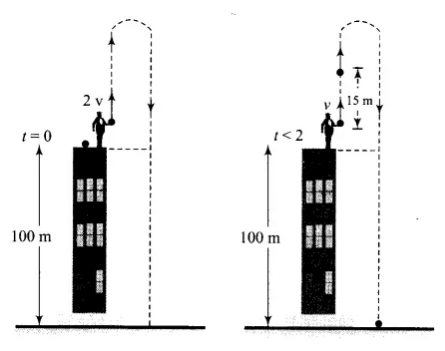 Let the speeds of the two balls (1 and 2) be v1 and v2 where: if v1 = 2v, v2 = v
Let the speeds of the two balls (1 and 2) be v1 and v2 where: if v1 = 2v, v2 = v
if y1 and y2 and the displacement covered by the balls 1 and 2, respectively, before coming to rest, then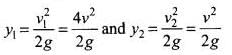
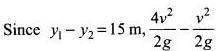

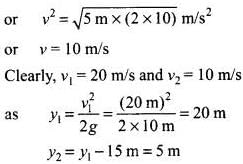
If t2 is the time taken by the ball 2 to cover a displacement of 5 m, then from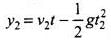
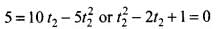
where t2 = 1 s
Since t1 (time taken by ball 1 to cover distance of 20 m) is 2 s, time interval between the two throws = t1 - t2 = 2s - 1s = 1s
Important note: We should be very careful when we are applying the equation of rectilinear motion. These equations are applicable only in case of constant acceleration.
Some important observations for motion under gravity:
- The motion is independent of the mass of the body, as in any equation of motion, mass is not involved. That is why a heavy and light body when released from the same height, reach the ground simultaneously and with same velocity, i.e., t = √(2h/g) and v = √2gh.
- In case of motion under gravity time taken to go up is equal to the time taken to fall down through the same distance.
Time of descent (t1) = time of ascent (t2) = u/g
Total time of flight T = tx + t2 = 2u/g
- In case of motion under gravity, the speed with which a body is projected up is equal to the speed with which it comes back to the point of projection.
As well as the magnitude of velocity at any point on the path is same whether the body is moving in upwards or downward direction. - A body is thrown vertically upwards. If air resistance is to be taken into account, then the time of ascent is less than the time of descent t2 > t1
Let u be the initial velocity of body, then time of ascent 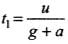 and
and 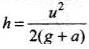
where g is acceleration due to gravity and a is retardation by air resistance and for upward motion both will act vertically downward.
For downward ‘motion a and g will act in opposite direction because a always act in direction opposite to motion and g always act vertically downward.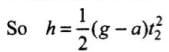
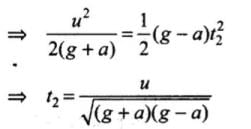
Comparing t1 and t2 we can say that t2 > t1, since (g + a) > (g - a)
FAQs on NCERT Exemplar: Motion in a Straight Line - 2 - NCERT Exemplar & Revision Notes for NEET
| 1. What is motion in a straight line? |  |
| 2. What are the different types of motion in a straight line? |  |
| 3. How is velocity related to motion in a straight line? |  |
| 4. What is the difference between speed and velocity in motion in a straight line? |  |
| 5. How is acceleration calculated in motion in a straight line? |  |





















