NCERT Exemplar: Thermodynamics | Physics Class 11 - NEET PDF Download
| Table of contents |

|
| Multiple Choice Questions I |

|
| Multiple Choice Questions II |

|
| Very Short Answer Type Questions |

|
| Short Answer Type Questions |

|
| Long Answer Type Questions |

|
Multiple Choice Questions I
Q.1. An ideal gas undergoes four different processes from the same initial state (Figure). Four processes are adiabatic, isothermal, isobaric and isochoric. Out of 1, 2, 3 and 4 which one is adiabatic.
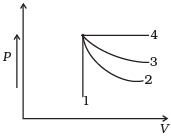
(a) 4
(b) 3
(c) 2
(d) 1
Ans. (c)
Solution.
4 is isobaric process, 1 is isochoric. Out of 3 and 2, 3 has the smaller slope (magnitude) hence is isothermal. Remaining process 2 is adiabatic.
Q.2. If an average person jogs, hse produces 14.5 × 103 cal/min. This is removed by the evaporation of sweat. The amount of sweat evaporated per minute (assuming 1 kg requires 580 × 103 cal for evaporation) is
(a) 0.25 kg
(b) 2.25 kg
(c) 0.05 kg
(d) 0.20 kg
Ans. (a)
Solution.
580 x 103 calories are needed to convert 1 kg H2O into steam
1 cal will produce sweat = 1/580 x 103
14.5 x 103 cal will produce sweat = 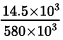
= 145/5800 kg per minute = 0.025 kg per min
Q.3. Consider P-V diagram for an ideal gas shown in Fig
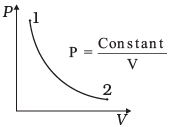
Out of the following diagrams (Figures), which represents the T-P diagram?
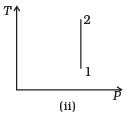
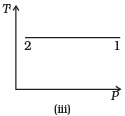
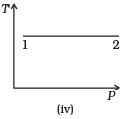
(a) (iv)
(b) (ii)
(c) (iii)
(d) (i)
Ans. (c)
Solution.
According to P-V diagram at constant temperature, P increases as V decreases. So, it is Boyle’s law in options (iii) and (iv). If P increases at constant temperature, volume V decreases. As in (iii) T-P diagram, P is smaller at 2 and larger at 1, which tallies with option (c).
Q.4. An ideal gas undergoes cyclic process ABCDA as shown in given P-V diagram (Fig.).
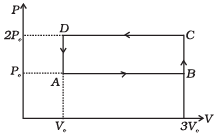
The amount of work done by the gas is
(a) 6PoVo
(b) -2 PoVo
(c) +2 PoVo
(d) +4 PoVo
Ans. (b)
Solution.
Work (∆W): Work can be defined as the energy that is transferred from one body to the other owing to a force that acts between them.
If P be the pressure of the gas in the cylinder, then force exerted by the gas on the piston of the cylinder F= PA.
In a small displacement of piston through dx, work done by the gas dW = F.dx = PA dx = PdV
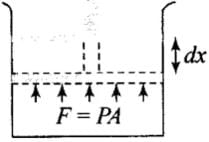
∴ Total amount of work done 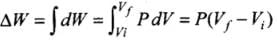
In P-V diagram or indicator diagram, the area under P-V curve represents work done.
W = area under P-V diagram
According to the P-V diagram given in the question,
Work done in the process ABCD = Area of rectangle ABCDA
= AB x BC = (3V0 - V0) x (2P0 - P0)
= 2V0 x P0 = 2P0V0
Since, the cyclic process is anti-clockwise, work done by the gas is negative, i.e., - 2P0V0. Hence there is a net compression in the gas.
Important point: In a cyclic process work dine is
1. positive if the cycle is clockwise.
2. negative if the cycle is anticlockwise.
Q.5. Consider two containers A and B containing identical gases at the same pressure, volume and temperature. The gas in container A is compressed to half of its original volume isothermally while the gas in container B is compressed to half of its original value adiabatically. The ratio of final pressure of gas in B to that of gas in A is
(a) 2γ-1
(b) (1/2)γ-1
(c) 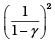
(d) 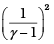
Ans. (a)
Solution.
According to the P-V diagram shown for the container A (which is going through isothermal process) and for container B (which is going through adiabatic process).
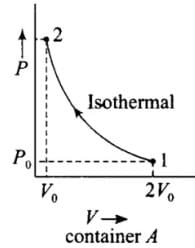
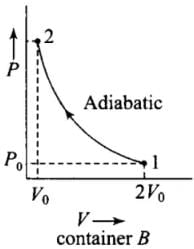
Both the process involves compression of the gas.
(i) Isothermal compression (gas A) during 1 → 2)
P1V1 = P2V2
⇒ P0(2V0)γ = P2(V0)γ
⇒ P0(2V0) = P2(V0)
(ii) Adiabatic compression, (gas B) (during 1 → 2)
P1V1γ = P2V2γ
⇒ P0(2V0)γ = P2(V0)γ
⇒ 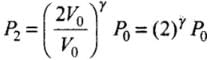
Hence 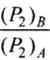 = Ratio of final pressure =
= Ratio of final pressure = 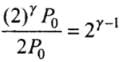
where, γ is ratio of specific heat capacities for the gas.
Q.6. Three copper blocks of masses M1, M2 and M3 kg respectively are brought into thermal contact till they reach equilibrium. Before contact, they were at T1, T2, T3 (T1 > T2 > T3 ). Assuming there is no heat loss to the surroundings, the equilibrium temprature T is (s is specific heat of copper)
(a) 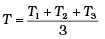
(b) 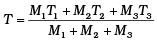
(c) 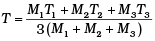
(d) 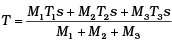
Ans. (b)
Solution.
According to question, since there is no net loss to the surroundings and the equilibrium temperature of the system is T.
Let us assume that T1,T2< T< T3.
Heat lost by M3 = Heat gained by M1+ Heat gained by M2
⇒ M3s(T3-T) = M1s(T-T1) + M2s(T-T2)
(where s is the specific heat of the copper material)
⇒ T[M1 + M2 + M3] = M3T3 + M1T1 + M2T2
⇒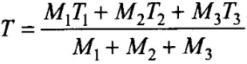
Multiple Choice Questions II
Q.7. Which of the processes described below are irreversible?
(a) The increase in temperature of an iron rod by hammering it.
(b) A gas in a small container at a temperature T1 is brought in contact with a big reservoir at a higher temperature T2 which increases the temperature of the gas.
(c) A quasi-static isothermal expansion of an ideal gas in cylinder fitted with a frictionless piston.
(d) An ideal gas is enclosed in a piston cylinder arrangement with adiabatic walls. A weight W is added to the piston, resulting in compression of gas.
Ans. (a, b, d)
Solution.
Reversible process: A reversible process is one which can be reversed in such a way that all changes occurring in the direct process are exactly repeated in the opposite order and inverse sense and no change is left in any of the bodies taking part in the process or in the surroundings.
The conditions for reversibility are:
- There must be complete absence of dissipative forces such as friction, viscosity, electric resistance etc.
- The direct and reverse processes must take place infinitely slowly.
- The temperature of the system must not differ appreciably from its surroundings.
Irreversible process: Any process which is not reversible exactly is an irreversible process. All natural processes such as conduction, radiation, radioactive decay etc. are irreversible. All practical processes such as free expansion, Joule-Thomson expansion, electrical heating of a wire are also irreversible.
(a) In this case internal energy of the rod is increased from external work done by hammer which in turn increases its temperature. So, the process cannot be retraced itself.
(b) In this process energy in the form of heat is transferred to the gas in the small container by big reservoir at temperature T2.
(c) In a quasi-static isothermal expansion, the gas is ideal, this process is reversible because the cylinder is fitted with frictionless piston.
(d) As the weight is added to the cylinder arrangement in the form of external pressure hence, it cannot be reversed back itself.
Q.8. An ideal gas undergoes isothermal process from some initial state i to final state f. Choose the correct alternatives.
(a) DU = 0
(b) DQ= 0
(c) DQ = DU
(d) DQ = DW
Ans.(a, d)
Solution.
First Law of Thermodynamics: It is a statement of conservation of energy in thermodynamical process.
According to it heat given to a system (∆Q) is equal to the sum of increase in its internal energy (AIT) and the work done (AW) by the system against the surroundings.
∆Q = ∆U + ∆W
According to the first law of thermodynamics. ∆AQ = ∆U + ∆Wbut
∆U ∝ ∆T
∆U = 0 [As ∆T = 0]
∆Q = ∆W, i.e., heat supplied in an isothermal change is used to do work against external surrounding.
Or
If the work is done on the system then equal amount of heat energy will be liberated by the system.
Q.9. Figure shows the P-V diagram of an ideal gas undergoing a change of state from A to B. Four different parts I, II, III and IV as shown in the figure may lead to the same change of state.
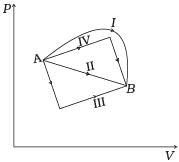
(a) Change in internal energy is same in IV and III cases, but not in I and II.
(b) Change in internal energy is same in all the four cases.
(c) Work done is maximum in case I
(d) Work done is minimum in case II.
Ans. (b, c)
Solution.

Internal energy (U): Internal energy of a system is the energy possessed by the system due to molecular motion and molecular configuration.
The energy due to molecular motion is called internal kinetic energy UK and that due to molecular configuration is called internal potential energyUp.
i.e., Total internal energy U= UK+ UP
(i) For an ideal gas, as there is no molecular attraction UP= 0
i.e., internal energy of an ideal gas is totally kinetic and is given by
U = UK= 3/2 RT
and change in internal energy ΔU = 3/2 μR
(ii) In case of gases whatever be the process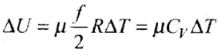
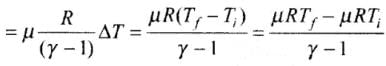
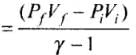
(iii) Change in internal energy in a cyclic process is always zero as for cyclic process Uf = Ui
So ΔU = Uf - Ui = 0
Change in internal energy does not depend on the path of the process. So it is called a point function, i.e., it depends only on the initial and final states (A and B) of the system, i.e., ΔU = Uf - Ui
Hence internal energy is same for all four paths I, II, III and IV.
The work done by an ideal gas is equal to the area bounded between P-V curve.
Work done from A to B, ΔWA→B = Area under the P-V curve which is maximum for the path I.
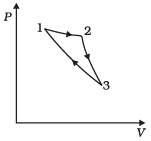
Q.10. Consider a cycle followed by an engine (Fig.)
1 to 2 is isothermal
2 to 3 is adiabatic
3 to 1 is adiabatic
Such a process does not exist because
(a) Heat is completely converted to mechanical energy in such a process, which is not possible.
(b) Mechanical energy is completely converted to heat in this process,which is not possible.
(c) Curves representing two adiabatic processes don’t intersect.
(d) Curves representing an adiabatic process and an isothermal process don’t intersect.
Ans. (a, c)
Solution.
(a) The given process is a cyclic process, i.e. it returns to the original state 1. And change in internal energy in a cyclic process is always zero as for cyclic process Uf = Ui So, ∆U = Uf – Ui = 0
Hence, total heat is completely converted to mechanical energy. Such a process is not possible by second law of thermodynamics.
(c) Here, two curves are intersecting, when the gas expands adiabatically from 2 to 3. It is not possible to return to the same state without being heat supplied, hence the process 3 to 1 cannot be adiabatic. So, we conclude that such a process does not exist because curves representing two adiabatic processes do not intersect.
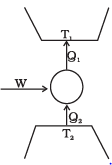
Q.11. Consider a heat engine as shown in Figure, Q1 and Q2 are heat added to heat bath T1 and heat taken from T2 in one cycle of engine. W is the mechanical work done on the engine.
If W > 0, then possibilities are:
(a) Q1 > Q2 > 0
(b) Q2 > Q1 > 0
(c) Q2 < Q1 < 0
(d) Q1 < 0, Q2 > 0
Ans.(a, c)
Solution.
Refrigerator or Heat Pump:
A refrigerator or heat pump is basically a heat engine run in reverse direction. It essentially consists of three parts:
Source:At higher temperature T1
Working substance: It is called refrigerant liquid ammonia and freon works as a working substance.
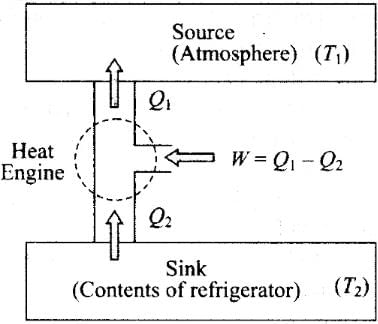
Sink: At lower temperature T2.
The working substance takes heat Q2 from a sink (contents of refrigerator) at lower temperature, has a net amount of work done W on it by an external agent (usually compressor of refrigerator) and gives out a larger amount of heat Q1, to a hot body at temperature T1 (usually atmosphere). Thus, it transfers heat from a cold body to a hot body at the expense of mechanical energy supplied to it by an external agent. The cold body is thus cooled more and more.
We know that the diagram represents the working of a refrigerator. So, we can write
Q1 = W + Q2
According to the problem, W > 0, then
⇒ W = Q1 - Q2 > 0
So there are two possibilities:
(a) If both Q1 and Q2 are positive,
⇒ Q1 > Q2 > 0
(c) If both Q1 and Q2 are negative,
Q2 < Q1 < 0
Very Short Answer Type Questions
Q.12. Can a system be heated and its temperature remains constant?
Ans.If the system does work against the surroundings so that it compensates for the heat supplied, the temperature can remain constant.
It is given that ΔT = 0 ⇒ ΔU = 0
∴ ΔQ = ΔU + ΔW
⇒ ΔQ = ΔW So heat supplied to the system is utilized in expansion system is isothermal.
Q.13. A system goes from P to Q by two different paths in the P-V diagram as shown in Figure. Heat given to the system in path 1 is 1000 J. The work done by the system along path 1 is more than path 2 by 100 J. What is the heat exchanged by the system in path 2?
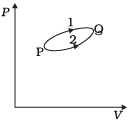
Ans. According to the first law of thermodynamics,
∆Q = AU + ∆W. Let us apply this for each path.
For path 1: Heat given Q1= +1000 J
Let work done for path 1 = W1 .
For path 2:
Work done (W2) = (WI –100)J
Heat given Q2– ?
As change in internal energy between two states for different path is same.
∆ U = Qi - W1= Q2 - W2
1000 – W! = Q2 - (W1– 100)
⇒Q2 = 1000 - 100 = 900 J
Q.14. If a refrigerator’s door is kept open, will the room become cool or hot? Explain.
Ans. A refrigerator is a heat engine it extracts heat from low temperature reservoir and transfer it to high temperature. If a refrigerator’s door is kept open, then room will become hot, because then refrigerator exhaust more heat into the room than earlier. In this way, temperature of the room increases and room becomes hot. No refrigerator is efficient. Thus it exhaust more heat into the room than it extract from it. Thus, a room cannot be cooled by keeping the door of a refrigerator open.
Q.15. Is it possible to increase the temperature of a gas without adding heat to it? Explain.
Ans. Yes. When the gas undergoes adiabatic compression, its temperature increases.
dQ = dU + dW
As dQ = 0 (adiabatic process)
so dU = -dW
In compression, work is done on the system So, dW = -ve
⇒ dU = + ve
So internal energy of the gas increases, i.e. its temperature increases.
Q.16. Air pressure in a car tyre increases during driving. Explain.
Ans. Volume of a car tyre is fixed. During driving, temperature of the gas increases while its volume remains constant. So, according to Charle’s law, at constant volume (V),
Pressure (P) ∝Temperature (T). Therefore, pressure of gas increases.
Short Answer Type Questions
Q.17. Consider a Carnot’s cycle operating between T1 = 500 K and T2 = 300K producing 1 k J of mechanical work per cycle. Find the heat transferred to the engine by the reservoirs.
Ans. EfficiencyofCarnot’sengine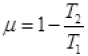
Temperature of source or reservoir = T1 = 500K
Temperature of sink = T2 = 300K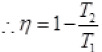
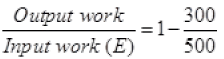
1000J/x = 1 - 0.6
1000/x = 0.4
x = 1000/0.4 = 2500 J.
Q.18. A person of mass 60 kg wants to lose 5 kg by going up and down a 10m high stairs. Assume he burns twice as much fat while going up than coming down. If 1 kg of fat is burnt on expending 7000 kilo calories, how many times must he go up and down to reduce his weight by 5 kg?
Ans. Gravitational potential energy (PE) of an object at height (h) is mgh. The energy losses by person in the form of fat will be utilised to increase PE of the person. As it is given that he burns twice as much fat while going up than coming down. Thus, the calorie consumed by the person in going up is mgh, and calorie consumed by the person in comming down is 1/2 mgh
According to the problem, height of the stairs = h = 10 m
Work done to burn 5 kg of fat
= (5 kg)(7000 x 103 cal) (4.2J/cal)
= 147 x 106 J
Work done towards burning of fat in one trip (up and down the stairs)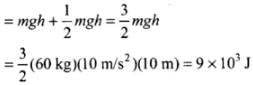
(as only half the work done while coming down is useful in burning fat)
∴ Number of times, the person has to go up and down the stairs (no. of trips required)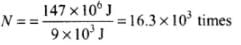
Q.19. Consider a cycle tyre being filled with air by a pump. Let V be the volume of the tyre (fixed) and at each stroke of the pump ∆V (V) of air is transferred to the tube adiabatically. What is the work done when the pressure in the tube is increased from P1 to P2?
Ans. Since the process is adiabatic, there is no exchange of heat in the process, Let, pressure is increased by AP and volume is increased by AV at each stroke.
For just before and after an stroke, we can write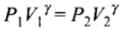
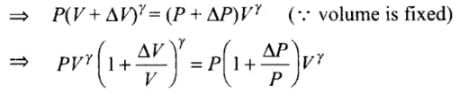
As ΔV << V, so by using binomial approximation we get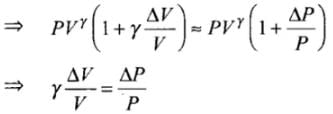
⇒ 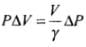
Hence, work done is increasing the pressure from P1 to P2 is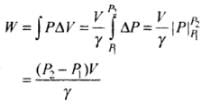
Important note: As ΔV is very small so we can also write this as dV, then the work done will be same as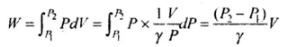
Q.20. In a refrigerator one removes heat from a lower temperature and deposits to the surroundings at a higher temperature. In this process, mechanical work has to be done, which is provided by an electric motor. If the motor is of 1kW power, and heat is transferred from –3°C to 27°C, find the heat taken out of the refrigerator per second assuming its efficiency is 50% of a perfect engine.
Ans. Carton’s engine is perfect heat engine operating between two temperature T1 and T2 (source and sink). Refrigerator is also carnot’s engine working in reverse order its efficiency in η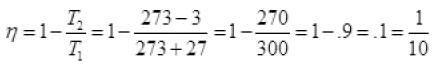
Efficiency of refrigerator’s 50% of perfect engine
∴ Efficiencyofrefrigerator = 50% of 1 = .5
Net efficiency = η' = 0.5 x 0.1 = 0.05
∴ Coefficient of performance 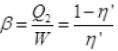
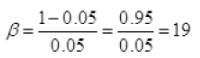
Q2 = 19% W.D. by motor on refrigerator
= 19 x 1 kW = 19 kJ/s
Q.21. If the co-efficient of performance of a refrigerator is 5 and operates at the room temperature (27 °C), find the temperature inside the refrigerator.
Ans.The performance of a refrigerator is expressed by means of “coefficient of performance” β which is defined as the ratio of the heat extracted from the cold body to the work needed to transfer it to the hot body.
i.e., 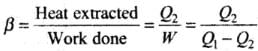
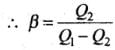
A perfect refrigerator is the one which transfers heat from cold to hot body without doing work.
i.e., W = 0 so that Q1 = Q2 and hence β =∞
According to the problem, coefficient of performance (ω) = 5
T1 = (27 + 273)K = 300K
Coefficient of performance (ω) = 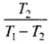
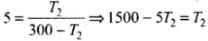
Q.22. The initial state of a certain gas is (Pi, Vi, Ti). It undergoes expansion till its volume becoms Vf. Consider the following two cases:
(a) the expansion takes place at constant temperature.
(b) the expansion takes place at constant pressure.
Plot the P-V diagram for each case. In which of the two cases, is the work done by the gas more?
Ans. The P-V diagram for each case is shown in the figure.
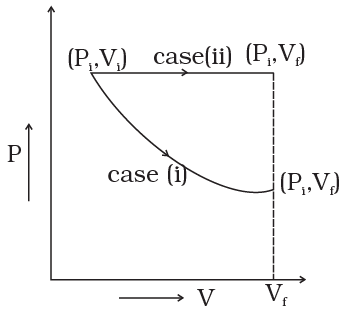
In case (i) Pi Vi = Pf Vf ; therefore process is isothermal. Work done = area under the PV curve so work done is more when the gas expands at constant pressure.
Long Answer Type Questions
Q.23. Consider a P-V diagram in which the path followed by one mole of perfect gas in a cylindrical container is shown in Figure.
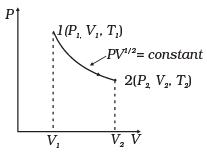
(a) Find the work done when the gas is taken from state 1 to state 2.
(b) What is the ratio of temperature T1/T2, if V2 = 2V1?
(c) Given the internal energy for one mole of gas at temperature T is (3/2) RT, find the heat supplied to the gas when it is taken from state 1 to 2, with V2 = 2V1.
Ans.(a)
Solution.
(a)
Work done by the gas (Let PV1/2 = A)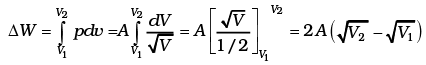
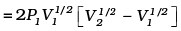
(b)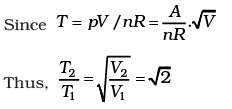
(c)
Then, the change in internal energy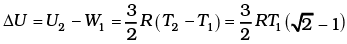
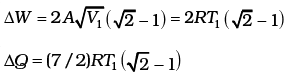
Q.24. A cycle followed by an engine (made of one mole of perfect gas in a cylinder with a piston) is shown in Fig.
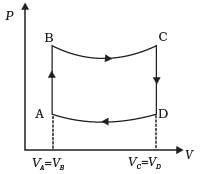
A to B : volume constant
B to C : adiabatic
C to D : volume constant
D to A : adiabatic
VC = VD = 2VA = 2VB
(a) In which part of the cycle heat is supplied to the engine from outside?
(b) In which part of the cycle heat is being given to the surrounding by the engine?
(c) What is the work done by the engine in one cycle? Write your answer in term of PA, PB, VA.
(d) What is the efficiency of the engine?
[γ = 5/3 for the gas], (Cv = 3/2 R for one mole)
Ans.
(a) A to B
(b) C to D
(c) 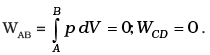
Similarly. 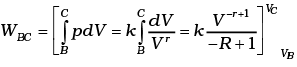
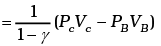
Similarly, 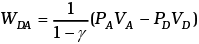
Now 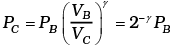
Similarly, PD = PA 2-γ
Total work done = WBC +WDA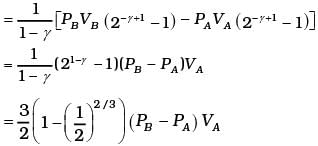
(d) Heat supplied during process A, B
dQAB = dUAB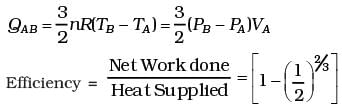
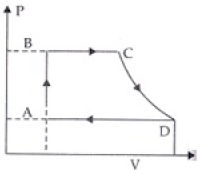
Q.25. A cycle followed by an engine (made of one mole of an ideal gas in a cylinder with a piston) is shown in Figure. Find heat exchanged by the engine, with the surroundings for each section of the cycle. (Cv = (3/2) R)
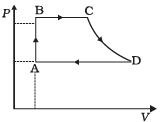
AB : constant volume
BC : constant pressure
CD : adiabatic
DA : constant pressure
Ans.
(a):For A → B, dV = 0
So, 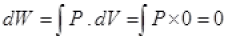
dW = 0
By 1st law of thermodynamics
dQ = dU + dW = dU + 0
∴ dQ = dU
(∵ dQ = nCvdT)
n = 1; Cv = 3/2 R
So, 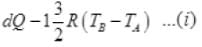
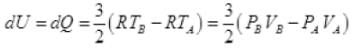
∴ Heat exchange [to system]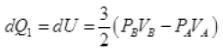
(b) For B to C, ΔP = 0 n = 1
dQ = dU + dW = Cv(dT) + PBdV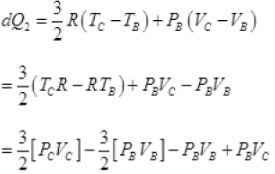
VA = VB and PB = PC
∴ 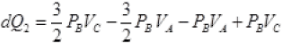
= 5/2 PBVC - 5/2PBVA
dQ2 = 5/2PB[VC - VA]
(c) For diagram C → D, adiabatic change
∴ dQ3 = 0 (No exchange of heat)
(d) For diagram D → A, ΔP = 0 Compression of gas from volume VD to VA at constant pressure hence heat exchange similar to part (b) i.e. Heat exchange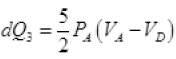
Q.26. Consider that an ideal gas (n moles) is expanding in a process given by P = f (V), which passes through a point (V0, P0). Show that the gas is absorbing heat at (P0, V0) if the slope of the curve P = f (V) is larger than the slope of the adiabat passing through (P0, V0).
Ans.Slope of P = f (V), curve at (Vo, Po) = f (Vo)
Slope of adiabat at (Vo, Po)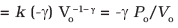
Now heat absorbed in the process P = f (V)
dQ = dV + dW
= nCvdT + P dV
Since T = (1/nR ) PV = (1/ nR ) V f (V)
dT = (1/nR ) [f (V) + V f′ (V)] dV
Thus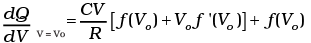
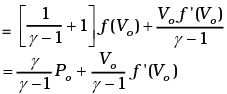
Heat is absorbed when dQ/dV > 0 when gas expands, that is when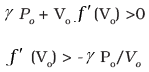
Q.27. Consider one mole of perfect gas in a cylinder of unit cross section with a piston attached (Fig.). A spring (spring constant k) is attached (unstretched length L) to the piston and to the bottom of the cylinder. Initially the spring is unstretched and the gas is in equilibrium. A certain amount of heat Q is supplied to the gas causing an increase of volume from Vo to V1.
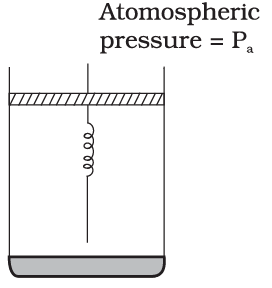
(a) What is the initial pressure of the system?
(b) What is the final pressure of the system?
(c) Using the first law of thermodynamics, write down a relation between Q, Pa, V, Vo and k.
Ans. (a): It is considered that piston is mass less and piston is balanced by atmospheric pressure (Pa). So the initial pressure of system inside the cylinder = Pa,
(b) On supply heat Q. Volume of gas increases from V0 to V1 and spring stretched also.
So increase in volume = V1 - V0
If displacement of piston is x then volume increase in cylinder)
= Area of base x height = A x x
A x x = V1 - V0 (A = area of cross section of cylinder)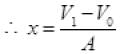
Force exerted by spring 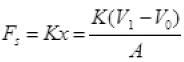
As the piston is of unit area of cross-section ∴ A = 1
Force due to spring = K(V1 - V0) on unit area can be say press due to spring = K(V1 - V0)
Final total pressure on gas Pf = Pa + K(V1 - V0)
(c) By Ist law of thermodynamics dQ = dU + dW
dU = CV(T - T0)
T = final temperature of gas
T0 = initial temperature of gas
n = 1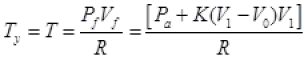
W.D. by gas = p. dV + increase in PE of spring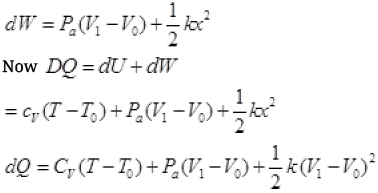
It is required relation.
|
96 videos|367 docs|98 tests
|
FAQs on NCERT Exemplar: Thermodynamics - Physics Class 11 - NEET
| 1. What is thermodynamics? |  |
| 2. What are the laws of thermodynamics? |  |
| 3. What is the difference between heat and work in thermodynamics? |  |
| 4. What is an ideal gas in thermodynamics? |  |
| 5. How is thermodynamics applied in engineering? |  |




















