NCERT Exemplar: Nuclei - 2 | Physics Class 12 - NEET PDF Download

SHORT ANSWER TYPE QUESTIONS

Q.16. Why do stable nuclei never have more protons than neutrons?
Ans. The reason is that protons, being charged particles, repel each other. This repulsion becomes so great in nuclei with more than 10 protons or so, that an excess of neutrons which produce only attractive forces, is required for stability.
Important point: As you get to heavier elements, with each new proton you add, there is a larger repulsive force. The nuclear force is attractive and stronger than the electrostatic force, but it has a finite range. So you need to add extra neutrons, which do not repel each other, to add extra attractive force. You eventually reach a point where the nucleus is just too big, and tends to decay via alpha decay or spontaneous fission.
To view this in quantum mechanical terms, the proton potential well is not as deep as the neutron well due to the electrostatic repulsion. [Due to the Pauli exclusion principle, you only get two particles per level (spin up and spin down)]. If one well is filled higher than the other, you tend to get a beta decay to even them out. As the nuclei get larger, the neutron well gels deeper as compared to the proton well and you get more neutrons than protons.

Q.17. Consider a radioactive nucleus A which decays to a stable nucleus C through the following sequence:
A → B → C
Here B is an intermediate nuclei which is also radioactive.
Considering that there are N₀ atoms of A initially, plot the graph showing the variation of number of atoms of A and B versus time.
Ans. Consider radioactive nucleus A have N₀ atoms of A initially; or at t = 0, N_A = N₀ (maximum) whole N_B = 0. As time increases, N_A decreases exponentially and the number of atoms of B increases. After some time N_B becomes maximum. As B is an intermediate nuclei which is also radioactive, it also start decaying and finally drop to zero exponentially by radioactive decay law. We can represent the situation as shown in the graph.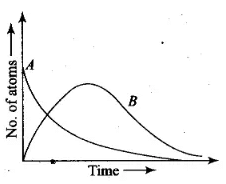

Q.18. A piece of wood from the ruins of an ancient building was found to have a ¹⁴C activity of 12 disintegrations per minute per gram of its carbon content. The ¹⁴C activity of the living wood is 16 disintegrations per minute per gram. How long ago did the tree, from which the wooden sample came, die? Given half-life of ¹⁴C is 5760 years.
Ans. Rate of disintegration in old wood sample of C-14 radioactive atoms is 12 atoms per min gm. Initially rate of disintegration of C-14 when the tree was live=16 atoms per min per gm.
T_1/2 of C-14 nuclei=5760 years
According to radioactive decay law,
N=N₀e^-λt or R=R₀e^-λt
12=16e^-λt

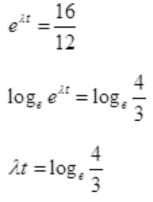
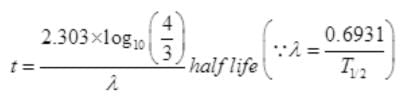
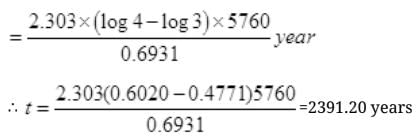
Q.19. Are the nucleons fundamental particles, or do they consist of still smaller parts? One way to find out is to probe a nucleon just as Rutherford probed an atom. What should be the kinetic energy of an electron for it to be able to probe a nucleon? Assume the diameter of a nucleon to be approximately 10^–15 m.
Ans. To detect the properties of nucleons inside the nucleus the wavelength of particle which may detect nucleons that must be of size of nucleons (10^-15 m). So the wavelength of particle which can detect the nucleons must be equal to or less than 10^-15
λ = 10^-15 m
λ = h/p
∵ E = hv = hc/λ    [∵c = vλ]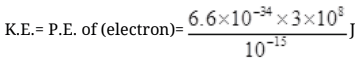


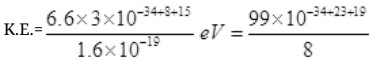
=12.4×10^-34+42=1.24×10¹×10⁺⁸
K.E. = 1.24×10⁹eV
So the K.E. of particle which may detect nucleon inside the nucleus must be of 1.24×10⁹ eV per particle.

Q.20. A nuclide 1 is said to be the mirror isobar of nuclide 2 if Z₁ =N₂ and Z₂ =N₁ .
(a) What nuclide is a mirror isobar of ²³₁₁Na ?
(b) Which nuclide out of the two mirror isobars have greater binding energy and why?
Ans.
Here Z is atomic number and N is no. of neutron in ₁₁Na²³
Z₁=11
N₁=23-11=12
Mirror isobar of ₁₁Na²³ is
Z₂ = N₁ = 12
So Mg is isobar of ₁₁Na²³
So ₁₂Mg²³ is the mirror isobar of ₁₁Na²³
(b) As the neutrons in ₁₂Mg²³ are ‘11’ and in ₁₁Na²³ are ‘12’ so, the number of neutrons in Na is larger than Mg and hence nuclear short range attractive forces in Na will be larger than repulsive electrostatic forces between proton-proton.
So, ₁₁Na²³ has more binding energy than ₁₂Mg²³

LONG ANSWER TYPE QUESTIONS

Q.21. Sometimes a radioactive nucleus decays into a nucleus which itself is radioactive. An example is: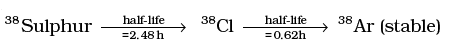
Assume that we start with 1000 ³⁸S nuclei at time t = 0. The number of ³⁸Cl is of count zero at t = 0 and will again be zero at t =∞ . At what value of t, would the number of counts be a maximum?
Ans.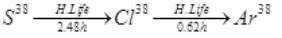

Initially at t=0, number of radioactive atoms of S³⁸ = N₁ and of Cl³⁸ are zero.
At any time t,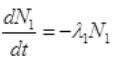
and N₁=N₀e^-λ1^t
It is the rate of formation of Cl³⁸ from S³⁸. Let N₂ is the number of of Cl³⁸ atoms (radioactive):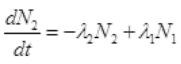

=λ₁N₀e^-λ1^t-λ₂N₂    ...(I)
Multiplying both sides by e^+λ2^t dt


Integrating both sides

∴ Cl³⁸ atom is formed after disintegration of S³⁸, so initially number of Cl³⁸ atoms are N₂=0.
at t=0, N₂=0,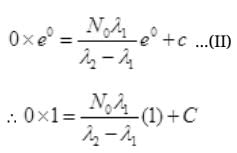



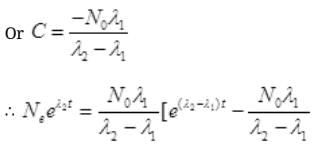
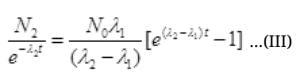
Multiplying E^-λ2^t to both sides we get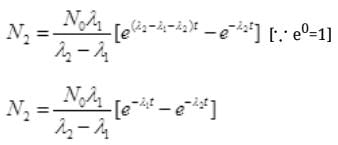


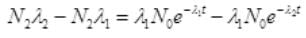
N₀ are the number of S₃₈ atoms
No. Are Cl³⁸ atoms after time ti will be N₂=N₀e^-λ2^t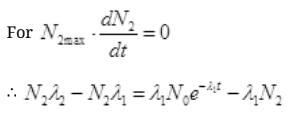


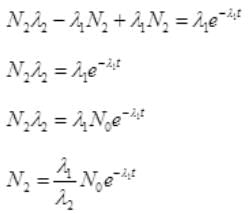
Put the value of N₂ in (III)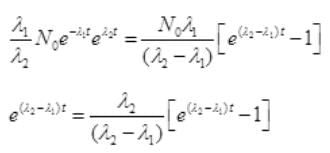

By cross multiplication and multiplying both sides by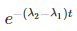








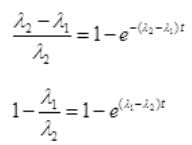
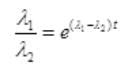
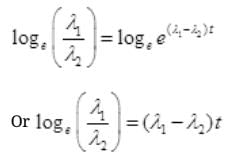
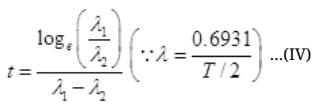
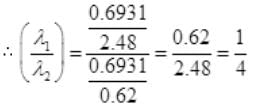
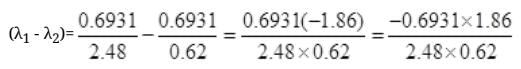
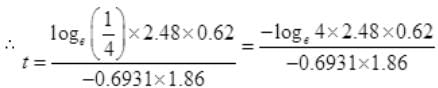
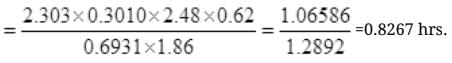
Number Cl³⁸ radioactive atoms will be maximum at N₂ = 0.8267 hrs.

Q.22. Deuteron is a bound state of a neutron and a proton with a binding energy B = 2.2 MeV. A γ -ray of energy E is aimed at a deuteron nucleus to try to break it into a (neutron + proton) such that the n and p move in the direction of the incident γ-ray.
If E = B, show that this cannot happen. Hence calculate how much bigger than B must E be for such a process to happen.
Ans. Binding energy (B) of deuteron = 2.2 MeV
Some part of energy of γ-ray is used up against binding energy B = 2.2 MeV and the rest part will impart K.E. to neutron and proton.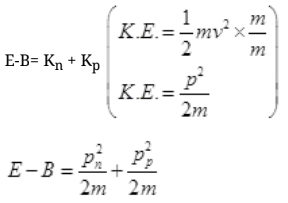

By law of conservation of momentum,
∴ P_n + p_p= momentum of γ-ray of Energy E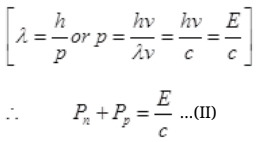

Case I: If E=B then from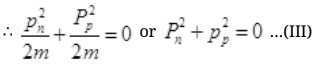

It can be possible if p_n= p_p=0 because square of non zero number can never zero.
If p_n=p_p=0 then equation IInd cannot be satisfied and the process cannot take place. From II,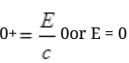 but energy E of γ ray cannot be zero.
Case II: if E>B or E=B+λ where λ will be very small than B then from (I),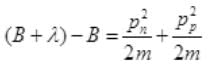




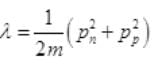
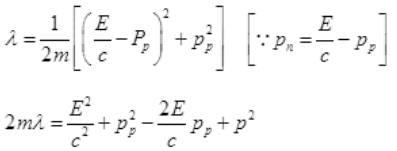
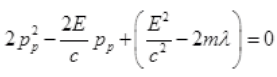
It is a quadratic equation so its solution by quadratic formula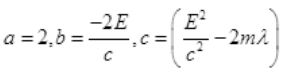


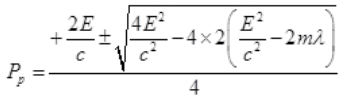
For a real and equal value of P_p discriminant must be zero as the value of p_p must be one.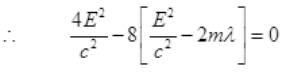



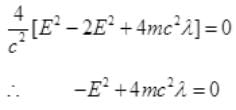
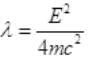
∵ λ is very small
So E=B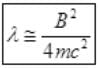


Q.23. The deuteron is bound by nuclear forces just as H-atom is made up of p and e bound by electrostatic forces. If we consider the force between neutron and proton in deuteron as given in the form of a Coulomb potential but with an effective charge e′ 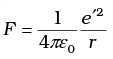 estimate the value of (e’/e) given that the binding energy of a deuteron is 2.2 MeV.
Ans. The binding energy of H atom in ground state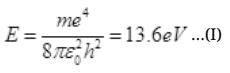

If proton and neutron had charge e’ each and governed by the same electrostatic force, then in the above equation we would need to replace electronic mass m by the reduced mass m’ of proton-neutron (as some mass of proton and neutron is used by binding energy) and electronic charge e is replaced by e’.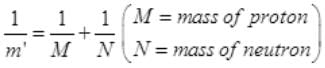


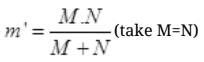
=M/2 ( if m = mass of electron)
m' = 1836m/2 = 918 m
∴ Binding Energy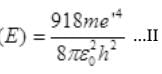
Dividing (II) by (i) we get,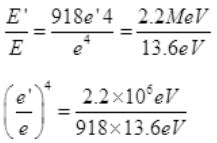

e'/e = 2200000/1248.48 = (176.21)^1/4
Required ratio e'/e = 3.64

Q.24. Before the neutrino hypothesis, the beta decay process was throught to be the transition,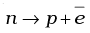

If this was true, show that if the neutron was at rest, the proton and electron would emerge with fixed energies and calculate them.Experimentally, the electron energy was found to have a large range.
Ans.  Neutron was at rest before β decay from neutron. Hence energy of neutron=E_n=m_nc² and momentum of neutron p_n=0 as its velocity is zero.
By the law of conservation of momentum,
P_n=p_p+ p_e (Beta)
O= p_p+ p_e
Let p_e=p_p then
⇒ |p_p|=|p_e|=p(eV)
Energy of proton = E_p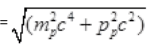 
Energy of electron
From conservation,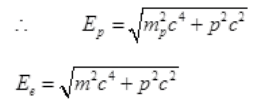

∴ By the law of conservation of energy,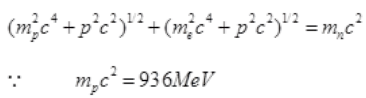

and m_nc² =938 MeV
and m_ec²= 0.5 meV
As the energy difference in neutron and proton is very small, pc will be small pc<<m_pc² while pc may be greater than m_ec² so by neglecting (m_ec²)²= (0.5)² (given)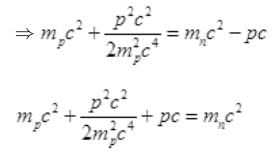

Again pc<<m_pc² so neglecting 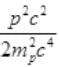 we get
Pc = m_nc²-m_pc² =938 MeV-936 MeV
Pc=2 MeV is the momentum
E=mc²
∵ E² = m²c⁴
E is the energy of either proton or neutron then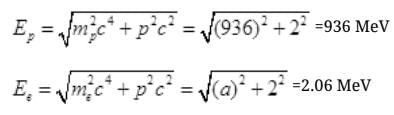


Q.25. The activity R of an unknown radioactive nuclide is measured at hourly intervals. The results found are tabulated as follows:

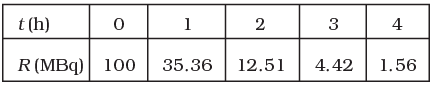
(i) Plot the graph of R versus t and calculate half-life from the graph.
(ii) Plot the graph of 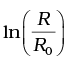 versus t and obtain the value of half-life from the graph.
Ans.
(i) Graph between R versus t is exponential curve. From the graph at slightly more 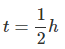 the R should be 50% so at R =50% the  t(h)=0.7h
=0.7×60 min
=42 min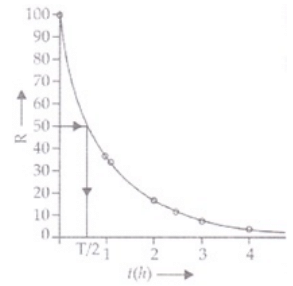

(ii) For Graph between 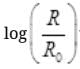 versus t(h)


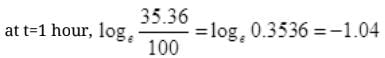
=2.302 log₁₀ 0.3536=1.04
at t=2 hours,
= 2.303log₁₀ 0.125 = -2.08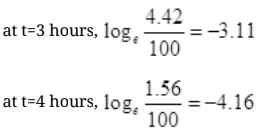

t (hours)	1	2	3	4
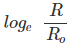	-1.04	-2.08	-311	-4.16

The graph showing the variation of 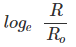 versus t(h) as follows:
We know that disintegration constant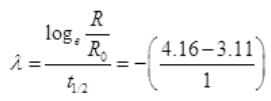

λ = -1.05 per hour
t_1/2 = 0.6931/λ = 0.6931/1.05
t_1/2 =  42 min


Q.26. Nuclei with magic no. of proton Z = 2, 8, 20, 28, 50, 52 and magic no. of neutrons N = 2, 8, 20, 28, 50, 82 and 126 are found to be very stable.
(i) Verify this by calculating the proton separation energy Sp for ¹²⁰Sn (Z = 50) and ¹²¹Sb = (Z = 51).
The proton separation energy for a nuclide is the minimum energy required to separate the least tightly bound proton from a nucleus of that nuclide. It is given by
S_p = (M_{Z–1, N} + M_H – M_Z,N )c².
Given ¹¹⁹In = 118.9058u, ¹²⁰Sn = 119.902199u, ¹²¹Sb = 120.903824u, ¹H = 1.0078252u.
(ii) What does the existence of magic number indicate?
Ans.
(i) S_p = (M_{Z–1, N} + M_H – M_Z,N )c²
Here in this formula M_Z-1 is the mass of atom of Z-1 atomic number.
M_Z is the mass of atom of mass number Z.
∴ M_Z-1= Mass of atom whose atomic number is 50-1=49.
It is ₄₉In¹¹⁹ in this case M_Z-1 = ₄₉In¹¹⁹ = 118.9058 and N=119 - 49 = 70.
S_p for ₅₀Sn¹²⁰=c²[118.9058+1.0078252-199.902199]
S_p for ₅₀Sn¹²⁰=0.0114362c²
Now for S_p of ₅₁Sb¹²¹
S_p= [M_z-1, _N+M_H-M_z,N]c²
Z=51, Z-1=50 for S_n
M_Z-1=mass of ₅₀Sn=199.902199 u
∴ S_p for ₅₁Sb¹²¹= [199.902199+1.0078252-120.903824]c²
= 0.0059912c²
∴ S_p(₅₀Sn¹²⁰)>S_p(₅₁Sb¹²¹)
(ii) The existence of magic numbers indicates that the shell structure of nucleus is similar to the shell structure of atom. This also explains the peaks in binding energy per nucleon curve.