NCERT Exemplar: Magnetism & Matter | NCERTs at Fingertips: Textbooks, Tests & Solutions - NEET PDF Download
MULTIPLE CHOICE QUESTIONS - I
Q.1. A toroid of n turns, mean radius R and cross-sectional radius a carries current I. It is placed on a horizontal table taken as x-y plane. Its magnetic moment m
(a) Is non-zero and points in the z-direction by symmetry.
(b) Points along the axis of the tortoid (m = mΦ)
(c) Is zero, otherwise there would be a field falling as 1/r3 at large distances outside the toroid.
(d) Is pointing radially outwards.
Ans. (c)
Solution.
Key concept: Toroid’. A toroid can be considered as a ring shaped closed solenoid. Hence it is like an endless cylindrical solenoid.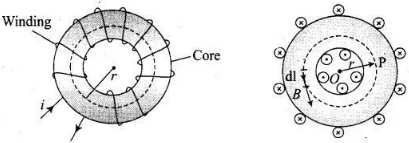 The magnetic field is only confined inside the body of a toroid in the form of concentric magnetic lines of force. For any point inside the empty space surrounded by toroid and outside the toroid, the magnetic field B is zero because the net current enclosed in these spaces is zero. Thus, the magnetic moment of toroid is zero.
The magnetic field is only confined inside the body of a toroid in the form of concentric magnetic lines of force. For any point inside the empty space surrounded by toroid and outside the toroid, the magnetic field B is zero because the net current enclosed in these spaces is zero. Thus, the magnetic moment of toroid is zero.
In general, if we take r as a large distance outside the toroid, then 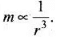 But this case is not possible here.
But this case is not possible here.
Q.2. The magnetic field of Earth can be modelled by that of a point dipole placed at the centre of the Earth. The dipole axis makes an angle of 11.3° with the axis of Earth. At Mumbai, declination is nearly zero. Then,
(a) The declination varies between 11.3° W to 11.3° E.
(b) The least declination is 0°.
(c) The plane defined by dipole axis and Earth axis passes through Greenwich. (d) Declination averaged over Earth must be always negative.
Ans. (a)
Solution.
The magnetic field lines of the earth resemble that of a hypothetical magnetic dipole located at the centre of the earth.
The axis of the dipole does not coincide with the axis of rotation of the earth and it is tilted at some angle (angle of declination). Here in this situation the angle of declination is approximately 11.3° with respect to the later. Here two possibilities arises as shown in the figure below.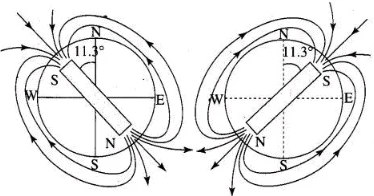
Hence, the declination varies between 11.3° W to 11.3° E.
Q.3. In a permanent magnet at room temperature
(a) Magnetic moment of each molecule is zero.
(b) The individual molecules have non-zero magnetic moment which are all perfectly aligned.
(c) Domains are partially aligned.
(d) Domains are all perfectly aligned
Ans. (d)
Solution.
Key concept: At room temperature permanent magnet behaves as a ferromagnetic substance for a long period of time.
At room temperature, the permanent magnet retains ferromagnetic property for a long period of time.
The individual atoms in a ferromagnetic material possess a dipole moment as in a paramagnetic material.
However, they interact with one another in such a way that they spontaneously align themselves in a common direction over a macroscopic volume called domain. Thus, we can say that in a permanent magnet at room temperature, domains are all perfectly aligned.
Q.4. Consider the two idealized systems: (i) a parallel plate capacitor with large plates and small separation and (ii) a long solenoid of length L >> R, radius of cross-section. In (i) E is ideally treated as a constant between plates and zero outside. In (ii) magnetic field is constant inside the solenoid and zero outside. These idealised assumptions, however, contradict fundamental laws as below:
(a) Case (i) contradicts Gauss’s law for electrostatic fields.
(b) Case (ii) contradicts Gauss’s law for magnetic fields.
(c) Case (i) agrees with 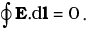
(d) Case (ii) contradicts 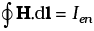
Ans. (b)
Solution.
Key concept: The electrostatic field lines, do not form a continuous closed path (this follows from the conservative nature of electric field) while the magnetic field lines form the closed paths.
According to the Gauss' law, 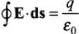 for electrostatic field. It does not contradict for electrostatic fields as the electric field lines do not form a continuous closed path.
for electrostatic field. It does not contradict for electrostatic fields as the electric field lines do not form a continuous closed path.
According to Gauss' law in magnetism,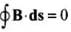
Which implies that number of magnetic field lines entering the Gaussian surface is equal to the number of magnetic field lines leaving it. Therefore case (ii) is not possible.
Q.5. A paramagnetic sample shows a net magnetisation of 8 Am–1 when placed in an external magnetic field of 0.6T at a temperature of 4K. When the same sample is placed in an external magnetic field of 0.2 T at a temperature of 16 K, the magnetisation will be
(a) 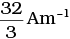
(b) 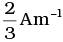
(c) 6 Am–1
(d) 2.4 Am–1 .
Ans. (b)
Solution.
Key concept: The magnetic susceptibility of paramagnetic substances is inversely proportional to its absolute temperature, i.e.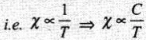
where C = 35 Curie constant, T= absolute temperature.
On increasing temperature, the magnetic susceptibility of paramagnetic materials decreases and vice versa. The magnetic susceptibility of ferromagnetic substances does not change according to Curie law and according to Curie law, magnetisation I or M = 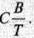
According to Curie law, we can deduce a formula for the relation between magnetic field induction, temperature and magnetisation.
Let us suppose, here I1 = 8 Am-1
B1 = 0.6 T, t1 = 4 K
B2 = 0.2 T, t2 = 16 K
I2 = ?
⇒ 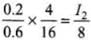
⇒ 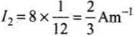
MULTIPLE CHOICE QUESTIONS - II
Q.6. S is the surface of a lump of magnetic material.
(a) Lines of B are necessarily continuous across S.
(b) Some lines of B must be discontinuous across S.
(c) Lines of H are necessarily continuous across S.
(d) Lines of H cannot all be continuous across S.
Ans. (a, d)
Solution.
Key concept: Here we are introducing properties of magnetic field lines (B), for any magnet, it forms continuous closed loops. This is unlike the electric dipole where these field lines begin from a positive charge and end on the negative charge or escape to infinity.
Also, magnetic intensity (H) outside any magnet is H = B/μ0 nd for inside the magnet H = B/μoμr, μr is the relative permeability o f material (magnetic).
Magnetic field lines for magnetic field 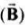 is continuous upon a transition through the interface.
is continuous upon a transition through the interface.
Also, magnetic intensity 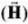 varies for inside and outside the lump. So, lines of
varies for inside and outside the lump. So, lines of  cannot all be continuous across S.
cannot all be continuous across S.
Q.7. The primary origin (s) of magnetism lies in
(a) Atomic currents.
(b) Pauli exclusion principle.
(c) Polar nature of molecules.
(d) Intrinsic spin of electron.
Ans. (a, d)
Solution.
The primary origin of magnetism lies in the fact that the electrons are revolving and spinning about the nucleus of an atom, and we know that an moving charge carries current along with it. We meant this current here as atomic current and which is responsible to produce an orbital magnetic moment. This atomic current gives rise to magnetism. The revolving and spinning about nucleus of an atom is called intrinsic spin of electron, which gives rise to spin magnetic moment. So, total magnetic moment is the sum of orbital magnetic moment and spin magnetic moment.
Q.8. A long solenoid has 1000 turns per metre and carries a current of 1 A. It has a soft iron core of µr = 1000 . The core is heated beyond the Curie temperature, Tc.
(a) The H field in the solenoid is (nearly) unchanged but the B field decreases drastically.
(b) The H and B fields in the solenoid are nearly unchanged.
(c) The magnetisation in the core reverses direction.
(d) The magnetisation in the core diminishes by a factor of about 108.
Ans. (a, d)
Solution.
Key concept: The magnetic field intensity H = nl, where n = number of turns per metre of a solenoid and I = current and B =μ0μrI.
Also, at normal temperature, a solenoid behaves as a ferromagnetic substance and at the temperature beyond the Curie temperature, it behaves as a paramagnetic substance.
We Know, for solenoid H = nI.
⇒ H= 1000 x 1 = 1000 Am
Thus, H is a constant, so it is nearly unchanged because on heating n and I remain constant.
But B = μ0 μr nI
= μ0n I μr
= k (constant) μr
but there is a large decrease in the susceptibility of the core on heating it beyond critical temperature, hence magnetic field will decrease drastically. Now, for magnetisation in the core, when temperature of the iron core of a solenoid is raised beyond Curie temperature, then it behaves as a paramagnetic material, where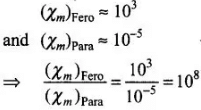
Q.9. Essential difference between electrostatic shielding by a conducting shell and magnetostatic shielding is due to
(a) Electrostatic field lines can end on charges and conductors have free charges.
(b) Lines of B can also end but conductors cannot end them.
(c) Lines of B cannot end on any material and perfect shielding is not possible.
(d) Shells of high permeability materials can be used to divert lines of B from the interior region.
Ans. (a, c, d)
Solution.
Electrostatic shielding is the phenomenon to block the effects of an electric field. The conducting shell can block the effects of an external field on its internal content or the effect of an internal field on the outside environment. For protecting a sensitive equipment from the external magnetic field it should be placed inside an iron cane (magnetic shielding). Magnetostatic shielding is done by using an enclosure made of a high permeability magnetic material to prevent a static magnetic field outside the enclosure from reaching objects inside it or to confine a magnetic field within the enclosure.
Q.10. Let the magnetic field on earth be modelled by that of a point magnetic dipole at the centre of earth. The angle of dip at a point on the geographical equator
(a) Is always zero.
(b) Can be zero at specific points.
(c) Can be positive or negative.
(d) Is bounded.
Ans. (b,c,d)
Solution.
Key concept: Angle of inclination or dip is the angle between the direction of intensity of total magnetic field of the earth and a horizontal line in the magnetic meridian.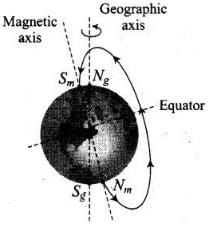
If the total magnetic field of the earth is modelled by a point magnetic dipole at the centre, then it is in the same plane of geographical equator, thus the angle of dip at a point on the geographical equator is bounded in a range from positive to negative value.
VERY SHORT ANSWER TYPE QUESTIONS
Q.11. A proton has spin and magnetic moment just like an electron. Why then its effect is neglected in magnetism of materials?
Ans. Spinning of a proton is negligible as compared to that of electron spin because its mass is very larger than the mass of an electron.
The comparison between the spinning of a proton and an electron can be done by comparing their magnetic dipole moment which can be given by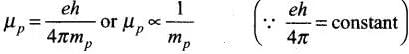
and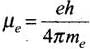
∴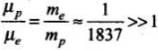
As we known proton is massive as compared to electron (mp>>me).
⇒ μp << μe
This shows the effect of magnetic moment of proton is neglected as compared to that of electron.
Q.12. A permanent magnet in the shape of a thin cylinder of length 10 cm has M = 106 A/m. Calculate the magnetisation current IM.
Ans. According to the problem, M (intensity o f magnetisation) = 106 A/m.
l(length) = 10 cm = 10 x 10-2 m= 0.1 m
and IM = magnetisation current
Here we know that 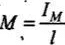
⇒ IM = M x l
= 106 x 0.1 = 105 A
Important point: Here, M = Intensity of magnetisation as its units are given as A/m.
Q.13. Explain quantitatively the order of magnitude difference between the diamagnetic susceptibility of N2 (~5 × 10–9) (at STP) and Cu (~10–5).
Ans. Key concept: Magnetic susceptibility: It is the property of the substance which shows how easily a substance can be magnetised. It can also be defined as the ratio of intensity of magnetisation (I) in a substance to the magnetic intensity (H) applied to the substance, i.e., XM =I/H.
According to the problem, we have
Density of nitrogen 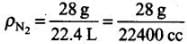
Also, density of copper 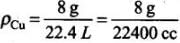
So, ratio of both densities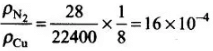
Also given 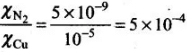
We know that, 
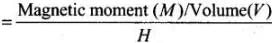
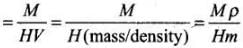

Therefore, we can say that magnitude difference or major difference between the diamagnetic susceptibility of N2 and Cu is 1.6 x 10-4.
Q.14. From molecular view point, discuss the temperature dependence of susceptibility for diamagnetism, paramagnetism and ferromagnetism.
Ans. Diamagnetism is due to the orbital motion of electrons in an atom developing magnetic moments opposite to applied field. Thus, the resultant magnetic moment of the diamagnetic material is zero, and hence the susceptibility x of diamagnetic material is not much affected by temperature.
Paramagnetism and ferromagnetism is due to alignments of atomic magnetic moments in the direction of the applied field. As temperature is raised, the alignment is disturbed, resulting decrease in susceptibility of both with increase in temperature.
Q.15. A ball of superconducting material is dipped in liquid nitrogen and placed near a bar magnet. (i) In which direction will it move? (ii) What will be the direction of it’s magnetic moment?
Ans. Key concept: A superconducting material and nitrogen both are diamagnetic in nature.
When a diamagnetic material is dipped in liquid nitrogen, it again behaves as a diamagnetic material. Thus, superconducting material will again behave as a diamagnetic material. When this diamagnetic material is placed near a bar magnet, it will be feebly magnetised opposite to the direction of magnetising field. (i) So it will move away from the magnet.
(i) So it will move away from the magnet.
(ii) Magnetic moment is from left to right and it is opposite to the direction of magnetic field.
SHORT ANSWER TYPE QUESTIONS
Q.16. Verify the Gauss’s law for magnetic field of a point dipole of dipole moment m at the origin for the surface which is a sphere of radius R .
Ans: Let us draw the figure for given situation,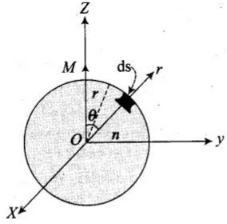 We have to prove that
We have to prove that 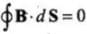 . This is called Gauss’s law in magnetism.Now, magnetic moment of dipole at origin O is along z-axis.
. This is called Gauss’s law in magnetism.Now, magnetic moment of dipole at origin O is along z-axis.
Let P be a point at distance r from O and OP makes an angle 9 with z-axis. Component of M along OP = M cos θ.
Now, the magnetic field induction at P due to dipole of moment M cos θ is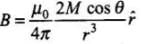
From the diagram, r is the radius of sphere with centre at O lying in yz-plane. Take an elementary area dS of the surface at P. Then,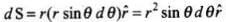
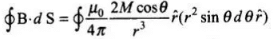
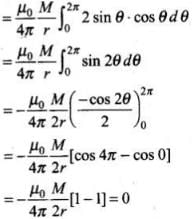
Q.17. Three identical bar magnets are riveted together at centre in the same plane as shown in Fig. 5.1. This system is placed at rest in a slowly varying magnetic field. It is found that the system of magnets does not show any motion. The north-south poles of one magnet is shown in the Fig. 5.1. Determine the poles of the remaining two.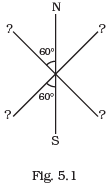 Ans. If the net force on the system is zero and net torque on the system is also zero, then the system will be in stable equilibrium. This is possible only when the poles of the remaining two magnets are as shown as below.
Ans. If the net force on the system is zero and net torque on the system is also zero, then the system will be in stable equilibrium. This is possible only when the poles of the remaining two magnets are as shown as below.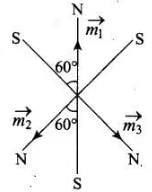
Q.18. Suppose we want to verify the analogy between electrostatic and magnetostatic by an explicit experiment. Consider the motion of (i) electric dipole p in an electrostatic field E and (ii) magnetic dipole m in a magnetic field B. Write down a set of conditions on E, B, p, m so that the two motions are verified to be identical. (Assume identical initial conditions.)
Ans. Electric field 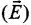 and magnetic field
and magnetic field 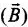 are related as
are related as
Key concept: Suppose the angle between  and
and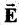 is θ . Torque on electric dipole of moment p in an electric field
is θ . Torque on electric dipole of moment p in an electric field 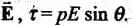
Let us assume that the angle between 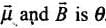
Torque on magnetic dipole moment 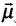 in magnetic field
in magnetic field
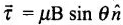
If these two motions are identical, then
pE sin θ = μB sin θ
⇒ pE = μB ...(i)
But, E = cB
∴ Putting this value in Eq. (i),
pcB = μB
⇒ 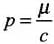
Putting this value in Eq. (i),
Q.19. A bar magnet of magnetic moment m and moment of inertia I (about centre, perpendicular to length) is cut into two equal pieces, perpendicular to length. Let T be the period of oscillations of the original magnet about an axis through the mid point, perpendicular to length, in a magnetic field B. What would be the similar period T′ for each piece?
Ans. Key concept: Time period in this type of S.H.M is T -2π 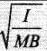
where,
T = time period
I = moment of inertia
m = mass of magnet
B = magnetic field
According to the problem, a magnet is oscillating in a uniform magnetic field, so we get the time period of oscillation as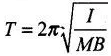
Here, 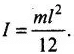
When magnet is cut into two equal pieces, perpendicular to length, then moment of inertia of each piece of magnet about an axis perpendicular to the length passing through its centre is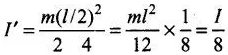
Magnetic dipole moment M' = M/2
Its time period of oscillation is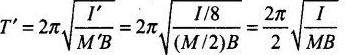
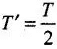
Q.20. Use (i) the Ampere’s law for H and (ii) continuity of lines of B , to conclude that inside a bar magnet, (a) lines of H run from the N pole to S pole, while (b) lines of B must run from the S pole to N pole.
Ans. Let C be the amperian loop. Then,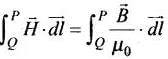
We know that the angle between B and dl is less than 90° inside the bar magnet. So, it is positive.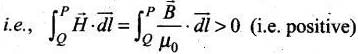
Hence, the lines of B must run from south pole (S) to north pole (N) inside the bar magnet. According to Ampere’s law,
∴ 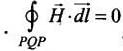
∴ 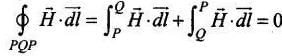
As 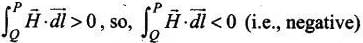
If angle between 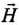 and
and  is more than 90°, so that cos θ is negative (it means the line of
is more than 90°, so that cos θ is negative (it means the line of 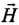 must run from N pole to S pole inside the bar magnet.)
must run from N pole to S pole inside the bar magnet.)
LONG ASNWER TYPE QUESTIONS
Q.21. Verify the Ampere’s law for magnetic field of a point dipole of dipole moment 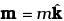 . Take C as the closed curve running clockwise along
. Take C as the closed curve running clockwise along
(i) the z-axis from z = a > 0 to z = R;
(ii) along the quarter circle of radius R and centre at the origin, in the first quadrant of x-z plane;
(iii) along the x-axis from x = R to x = a, and
(iv) along the quarter circle of radius a and centre at the origin in the first quadrant of x-z plane.
Ans. Consider a plane on x-z plane on which there are two loops (of radius R and a)and a point dipole on origin of dipole moment M(as shown in the figure). From P to Q, every point on the z-axis lies at the axial line of magnetic dipole of moment M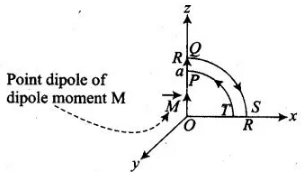 Magnetic field induction at a point distance r from the magnetic dipole of moment is
Magnetic field induction at a point distance r from the magnetic dipole of moment is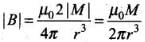
(i) Along z-axis from P to Q,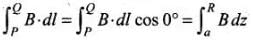
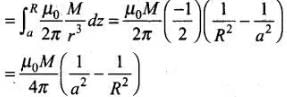
(ii) Along the quarter circle QS of radius R is given in the figure below: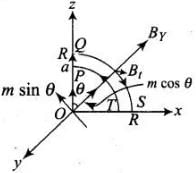 The point A lies on the equatorial line of the magnetic dipole of moment M sin 6. Magnetic field at point A on the circular arc is
The point A lies on the equatorial line of the magnetic dipole of moment M sin 6. Magnetic field at point A on the circular arc is
∴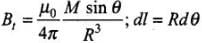
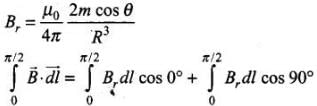
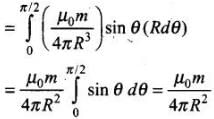
(iii) Along x-axis over the path ST, consider the figure given ahead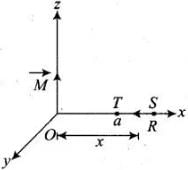 From figure, every point lies on the equatorial line of magnetic dipole. Magnetic field induction at a point distance x from the dipole is
From figure, every point lies on the equatorial line of magnetic dipole. Magnetic field induction at a point distance x from the dipole is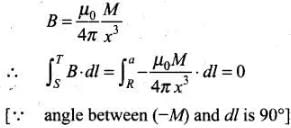
(iv) Along the quarter circle TP of radius a. Consider the figure given below: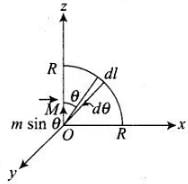 From case (ii), we get line integral of B along the quarter circle TP of radius a is circular arc TP.
From case (ii), we get line integral of B along the quarter circle TP of radius a is circular arc TP.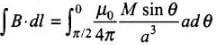
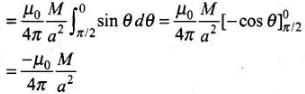
∴ 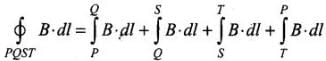
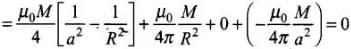
Q.22. What are the dimensions of χ, the magnetic susceptibility? Consider an H-atom. Guess an expression for χ, upto a constant by constructing a quantity of dimensions of χ, out of parameters of the atom: e, m , v, R and µ0 . Here, m is the electronic mass, v is electronic velocity, R is Bohr radius. Estimate the number so obtained and compare with the value of 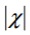 ~ 10–5 for many solid materials.
~ 10–5 for many solid materials.
Ans. Key concept: Magnetic susceptibility. It is the property of the substance which shows how easily a substance can be magnetised. It can also be defined as the ratio of intensity of magnetisation (I) in a substance to the magnetic intensity (H) applied to the substance, i.e. 
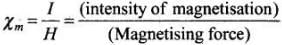
As I and H both have same units and dimensions, hence χ has no dimensions. In this problem, x is related with e, m, v, R and μo. We know that dimensions of 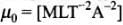
From Biot-Savart’s law,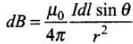
⇒ 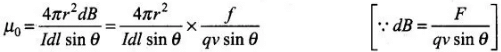
∴ Dimensions of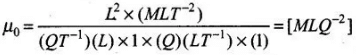
where Q is the dimension of charge.
As χ is dimensionless, it should have no involvement of charge Q in its dimensional formula. It will be so if μo and e together should have the value μ0e2, as e has the dimensions of charge.
Let χ = μ0e2mavbRc
where a, b, c are the power of m, v and R respectively, such that relation (i) is satisfied.
Dimensional equation of (i) is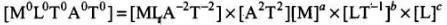
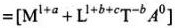
Equating the powers of M, L and T, we get
0 = 1 + a ⇒ a = - 1,0 = 1 + + c ...(ii)
0 = -b ⇒ b = 0, 0 = 1 + 0 + c or c = -1
Putting values in Eq. (i), we get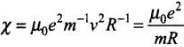
Here,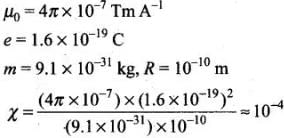
Q.23. Assume the dipole model for earth’s magnetic field B which is given by BV = vertical component of magnetic field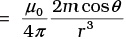 Bv = Horizontal component of magnetic field =
Bv = Horizontal component of magnetic field = 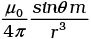 θ = 90° – latitude as measured from magnetic equator.
θ = 90° – latitude as measured from magnetic equator.
Find loci of points for which (i)  is minimum; (ii) dip angle is zero; and (iii) dip angle is ± 45°.
is minimum; (ii) dip angle is zero; and (iii) dip angle is ± 45°.
Ans. (a)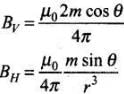
These are the components of B to net magnetic field will be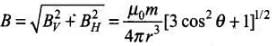
From above equation, the value o f B is minimum, if cos θ = π/2. θ = π/2 Thus, B is minimum at the magnetic equator.
(b) Angle of dip,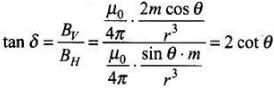 ...(i)
...(i)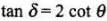
For dip angle is zero i.e., 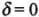
cot θ = 0
θ = π/2
For this value of θ angle of dip is vanished. It means that locus is again magnetic equator.
(c) 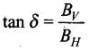
Angle of dip i.e., 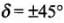

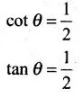
⇒ θ = tan -1 (2)
Thus θ = tan-1 (2) is the locus.
Q.24. Consider the plane S formed by the dipole axis and the axis of earth. Let P be point on the magnetic equator and in S. Let Q be the point of intersection of the geographical and magnetic equators. Obtain the declination and dip angles at P and Q.
Ans. Let point P is in the plane, S needle is in north, so the declination is zero.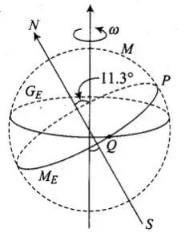
From figure,
For point P : Since point P lies in plane S formed by the dipole axis and the axis of the Earth, declination is zero,
For point Q : Since point Q lies on the magnetic equator, angle of dip is zero. Thus the angle of declination is 11.3°
Q.25. There are two current carrying planar coils made each from identical wires of length L. C1 is circular (radius R ) and C2 is square (side a).
They are so constructed that they have same frequency of oscillation when they are placed in the same uniform B and carry the same current. Find a in terms of R.
Ans. According to the problem C1 circular coil of radius R, length L, number of turns per unit length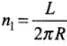
C2 = square of side a and perimeter L, number of turns per unit length n2 =L/4a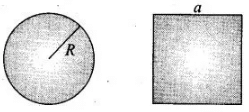
Magnetic moment of C1
⇒ m1 = n1iA1 (where i is the current in the coil)
Magnetic moment of C2
⇒ m2 = n2iA2 (where i is the current in the coil)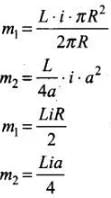
Moment of inertia of  ...(i)
...(i)
Moment of inertia of 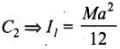 ...(ii) (where M is the mass of coil)
...(ii) (where M is the mass of coil)
Frequency of 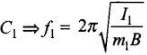 ...(iii)
...(iii)
Frequency of 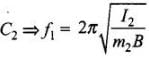 ...(iv)
...(iv)
According to problem, f1 = f2
Substituting the values from Eqs. (i), (ii), (iii) and (iv) (and also substitute the values of m1 and m2 in equation (iii) and (iv))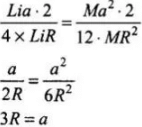
Thus, the value of a is 3R.
|
237 docs|243 tests
|
FAQs on NCERT Exemplar: Magnetism & Matter - NCERTs at Fingertips: Textbooks, Tests & Solutions - NEET
| 1. What is magnetism and how does it relate to matter? |  |
| 2. How is a magnet different from a magnetic material? |  |
| 3. What are the different types of magnets? |  |
| 4. How does magnetism play a role in everyday life? |  |
| 5. What is the relationship between magnetism and electricity? |  |
















