NCERT Exemplar: Electromagnetic Induction | Physics Class 12 - NEET PDF Download
MULTIPLE CHOICE QUESTIONS
Q.1. A square of side L meters lies in the x-y plane in a region, where the magnetic field is given by 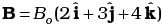 where Bo is constant. The magnitude of flux passing through the square is
where Bo is constant. The magnitude of flux passing through the square is
(a) 2 Bo L2 Wb.
(b) 3 Bo L2 Wb.
(c) 4 Bo L2 Wb.
(d) 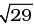 Bo L2 Wb.
Bo L2 Wb.
Ans. (c)
Solution.
Magnetic flux is defined as the total number of magnetic lines of force passing normally through an area placed in a magnetic field and is equal to the magnetic flux linked with that area.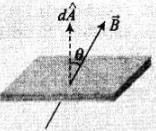 For elementary area dA of a surface flux linked dΦ= BdA cos 6 or
For elementary area dA of a surface flux linked dΦ= BdA cos 6 or 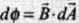
So, Net flux through the surface 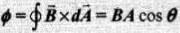
In this problem,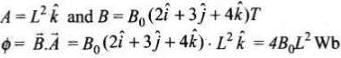
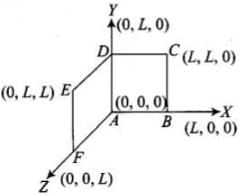
Q.2. A loop, made of straight edges has six corners at A(0,0,0), B(L,O,0) C(L ,L ,0) , D (0,L,0) E (0,L,L ) a n d F (0,0,L). A magnetic field 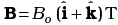 is present in the region. The flux passing through the loop ABCDEFA (in that order) is
is present in the region. The flux passing through the loop ABCDEFA (in that order) is
(a) Bo L2 Wb.
(b) 2 Bo L2 Wb.
(c) √2 Bo L2 Wb.
(d) 4 Bo L2 Wb.
Ans. (b)
In this problem first we have to analyse area vector, loop ABCDA lies in x - y plane whose area vector 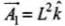 whereas loop ADEFA lies in y - z plane whose area vector
whereas loop ADEFA lies in y - z plane whose area vector
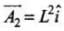
And the magnetic flux is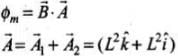
and 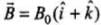
Now,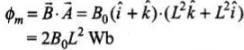
Q.3. A cylindrical bar magnet is rotated about its axis (Fig 6.1). A wire is connected from the axis and is made to touch the cylindrical surface through a contact. Then
(a) A direct current flows in the ammeter A.
(b) No current flows through the ammeter A.
(c) An alternating sinusoidal current flows through the ammeter A with a time period T=2π/ω.
(d) A time varying non- sinusoidal current flows through the ammeter A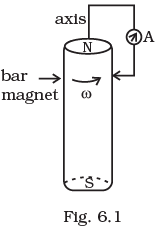 Ans. (b)
Ans. (b)
Solution.
Key concept: The phenomenon of electromagnetic induction is used in this problem. Whenever the number of magnetic lines of force (magnetic flux) passing through a circuit changes (or a moving conductor cuts the magnetic flux) an emf is produced in the circuit (or emf induces across the ends of the conductor) is called induced emf. The induced emf persists only as long as there is a change or cutting of flux.
When cylindrical bar magnet is rotated about its axis, no change in flux linked with the circuit takes place, consequently no emf induces and hence, no current flows through the ammeter A. Hence the ammeter shows no deflection.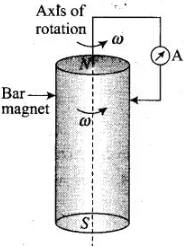
Q.4. There are two coils A and B as shown in Fig 6.2. A current starts flowing in B as shown, when A is moved towards B and stops when A stops moving. The current in A is counterclockwise. B is kept stationary when A moves. We can infer that
(a) There is a constant current in the clockwise direction in A.
(b) There is a varying current in A.
(c) There is no current in A.
(d) There is a constant current in the counterclockwise direction in A.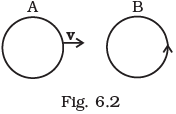
Ans. (d)
Solution.
Key concept: Due to variation in the flux linked with coil B an emf will be induced in coil B. Current in coil B becomes zero when coil A stops moving, it is possible only if the current in coil A is constant. If the current in coil A would be variable, there must be some changing flux and then there must be an induced emf. Hence an induced current will be in coil B even when coil A is not moving.
Q.5. Same as problem 4 except the coil A is made to rotate about a vertical axis (Fig 6.3). No current flows in B if A is at rest. The current in coil A, when the current in B (at t = 0) is counterclockwise and the coil A is as shown at this instant, t = 0, is
(a) Constant current clockwise.
(b) Varying current clockwise.
(c) Varying current counterclockwise.
(d) Constant current counterclockwise.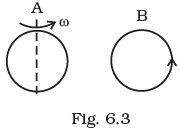 Ans. (a)
Ans. (a)
Solution.
Key concept: In this problem, the Lenz’s law is applicable so let us introduce Lenz’s law first.
Lenz’s law gives the direction of induced emf/induced current. According to this law, the direction of induced emf or current in a circuit is such as to oppose the cause that produces it. This law is based upon law of conservation of energy.
When the current in coil B (at t= 0) is counter-clockwise and the coil A is considered above it. The counter clockwise flow of the current in coil B is equivalent to north pole of magnet and magnetic field lines are eliminating upward to coil A. When coil A starts rotating at t = 0, the current in A is constant along clockwise direction by Lenz’s rule.
Q.6. The self inductance L of a solenoid of length l and area of cross-section A, with a fixed number of turns N increases as
(a) l and A increase.
(b) l decreases and A increases.
(c) l increases and A decreases.
(d) both l and A decrease.
Ans. (b)
Solution.
Key concept: The self inductance L of a solenoid depends on various factor like geometry and magnetic permeability of the core material.
L = μr μ0 n2 Al
where, n = N/l (no. of turns per unit length)
1. No. of turns: Larger the number of turns in solenoid, larger is its self inductance.
2. Area of cross section: Larger the area of cross section of the solenoid, larger is its self inductance.
3. Permeability of the core material. The self inductance of a solenoid increases μr times if it is wound over an iron core of relative permeability μr.
The long solenoid of cross-sectional area A and length l, having A turns, filled inside of the solenoid with a material of relative permeability (e.g., soft iron, which has a high value of relative permeability) then its self inductance is L = μrμ0 N2 A/l
So, the self inductance L of a solenoid increases as l decreases and A increases because L is directly proportional to area and inversely proportional to length.
Important point: The self and mutual inductance of capacitance and resistance depend on the geometry of the devices as well as permittivity/ permeability of the medium.
Q.7. A metal plate is getting heated. It can be because
(a) A direct current is passing through the plate.
(b) It is placed in a time varying magnetic field.
(c) It is placed in a space varying magnetic field, but does not vary with time.
(d) A current (either direct or alternating) is passing through the plate.
Ans. (a, b, c)
Solution.
Key concept: Eddy Current: When a changing magnetic flux is applied to a bulk piece of conducting material, then circulating currents called eddy currents are induced in the material. Because the resistance of the bulk conductor is usually low, eddy currents often have large magnitudes and heat up the conductor.
(1) These are circulating currents like eddies in water.
(2) Experimental concept is given by Focault, hence also named as “Focault current”.
(3) The production of eddy currents in a metallic block leads to the loss of electric energy in the form of heat.
(4) By lamination, slotting processes, the resistance path for circulation of eddy current increases, resulting into weakening them and also reducing losses causes by them.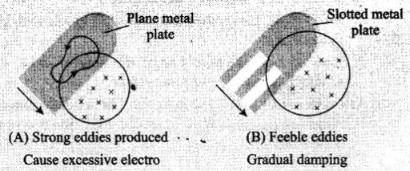
A metal plate is getting heated when a DC or AC current is passed through the plate, known as heating effect of current. This current (called eddy current) is induced in the plate when a metal plate is subjected to a time varying magnetic field, i.e., the magnetic flux linked with the plate changes and eddy currents comes into existence which make the plate hot.
Q.8. An e.m.f is produced in a coil, which is not connected to an external voltage source. This can be due to
(a) The coil being in a time varying magnetic field.
(b) The coil moving in a time varying magnetic field.
(c) The coil moving in a constant magnetic field.
(d) The coil is stationary in external spatially varying magnetic field, which does not change with time.
Ans. (a, b, c)
Solution.
Key concept: As we know whenever the number of magnetic lines of force (magnetic flux) passing through a circuit changes, an emf is produced in the circuit called induced emf. The induced emf persists only as long as there is a change or cutting of flux.
In this problem, magnetic flux linked with the isolated coil changes when the coil is placed in the region of a time varying magnetic field, the coil moving in a constant magnetic field or in time varying magnetic field.
Q.9. The mutual inductance M12 of coil 1 with respect to coil 2
(a) Increases when they are brought nearer.
(b) Depends on the current passing through the coils.
(c) Increases when one of them is rotated about an axis.
(d) Is the same as M21 of coil 2 with respect to coil 1.
Ans. (a, d)
Solution.
Key concept: Mutual Induction: Whenever the current passing through a coil or circuit changes, the magnetic flux linked with a neighbouring coil or circuit will also change. Hence an emf will be induced in the neighbouring coil or circuit. This phenomenon is called ‘mutual induction’.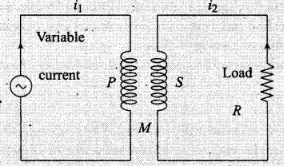
According to faraday's second law emf induces in secondary 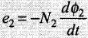 ,
,
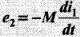
The mutual inductance M12 Of coil 1 w.r.t. coil 2 increases when they are brought nearer and is the same as M21 of coil 2 with respect to coil 1.
M12, i.e., mutual inductance of solenoid S1 with respect to solenoid S2 is given by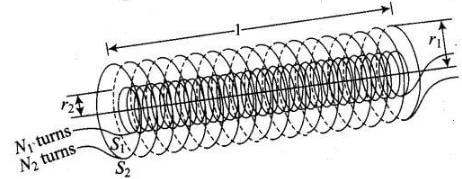 where signs are as usual.
where signs are as usual.
Also, M21, i.e., mutual inductance of solenoid S2 with respect to solenoid S1 is given by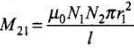
So, we have M12 = M21 = M
Q.10. A circular coil expands radially in a region of magnetic field and no electromotive force is produced in the coil. This can be because
(a) The magnetic field is constant.
(b) The magnetic field is in the same plane as the circular coil and it may or may not vary.
(c) The magnetic field has a perpendicular (to the plane of the coil) component whose magnitude is decreasing suitably.
(d) There is a constant magnetic field in the perpendicular (to the plane of the coil) direction.
Ans. (b, c)
Solution.
Key concept: As we know whenever the number of magnetic lines of force (magnetic flux) passing through a circuit changes an emf is produced in the circuit called induced emf. The induced emf persists only as long as there is a change or cutting of flux.
The induced emf is given by rate of change of magnetic flux linked with the circuit, i.e., e = -dФ/dt
According to the problem there is no electromotive force produced in the coil. Then the various arrangement are to be thought of in such a way that the magnetic flux linked with the coil does not change even if the coil is placed and expanded in magnetic field.
When circular coil expands radially in a region of magnetic field such that the magnetic field is in the same plane as the circular coil or we can say that direction of magnetic field is perpendicular to the direction of area (increasing) so that their dot product is always zero and hence change in magnetic flux is also zero.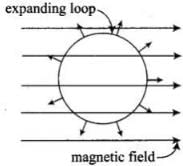 Or
Or
The magnetic field has a perpendicular (to the plane of the coil) component whose-magnitude is decreasing suitably in such a way that the dot product of magnetic field and surface area of plane of coil remain constant at every instant.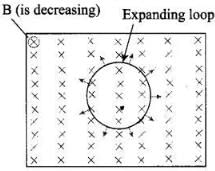
VERY SHORT ANSWER TYPE QUESTIONS
Q.11. Consider a magnet surrounded by a wire with an on/off switch S (Fig 6.4). If the switch is thrown from the off position (open circuit) to the on position (closed circuit), will a current flow in the circuit? Explain.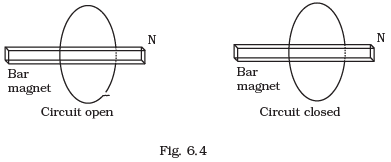 Ans. Key concept: The total number of magnetic lines of force passing normally through an area placed in a magnetic field is equal to the magnetic flux linked with that area.
Ans. Key concept: The total number of magnetic lines of force passing normally through an area placed in a magnetic field is equal to the magnetic flux linked with that area.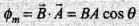
(θ is the angle between area vector and magnetic field vector)
Whenever the number of magnetic lines of force (magnetic flux) passing through a circuit changes an emf is produced in the circuit called induced emf. The induced emf persists only as long as there is a change or cutting of flux. The induced emf is given by rate of change of magnetic flux linked with the circuit i.e, e= – dФ/dt . so flux linked will change when either magnetic field, area or the angle between B and A changes.
If the switch is closed, the circuit will complete. But to induce emf in the circuit, we need:
(i) a changing magnetic field, but the bar magnet is stationary so it is not possible in this situation.
(ii) A changing area, which is also not possible because area is also constant as coil is not expanding or compressed.
(iii) Angle between B bar and A bar changes, which is also not possible in this situation because orientation of bar magnet and coil is fixed.
Thus, no change in magnetic flux linked with coil occur, hence no electromotive force is induced in the coil and hence no current will flow in the circuit.
Q.12. A wire in the form of a tightly wound solenoid is connected to a DC source, and carries a current. If the coil is stretched so that there are gaps between successive elements of the spiral coil, will the current increase or decrease? Explain.
Ans. Key concept: Lenz ‘s Law:
This law gives the direction of induced emf/induced current. According to this law, the direction of induced emf or current in a circuit is such as to oppose the cause that produces it. This law is based upon the law of conservation of energy.
(1) When AT-pole of a bar magnet moves towards the coil, the flux associated with the loop increases and an emf is induced in it. Since the circuit of loop is closed, induced current also flows in it.
(2) Cause of this induced current, is approach of north pole and therefore to oppose the cause, i.e., to repel the approaching north pole, the induced current in loop is in such a direction so that the front face of loop behaves as north pole. Therefore induced current as seen by observer O is in anticlockwise direction (figure).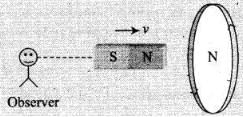 According to the given situation as the coil is stretched so that there are gaps between successive elements of the spiral coil, i.e., the wires are pulled apart which lead to the flux leak through the gaps. According to Lenz’s law, the emf induced in these spirals must oppose this decrease in magnetic flux, which can be done by an increase in current. So, the current will increase.
According to the given situation as the coil is stretched so that there are gaps between successive elements of the spiral coil, i.e., the wires are pulled apart which lead to the flux leak through the gaps. According to Lenz’s law, the emf induced in these spirals must oppose this decrease in magnetic flux, which can be done by an increase in current. So, the current will increase.
Q.13. A solenoid is connected to a battery so that a steady current flows through it. If an iron core is inserted into the solenoid, will the current increase or decrease? Explain.
Ans. This problem is based on Lenz’s law and according to this law, the direction of induced emf or current in a circuit is such as to oppose the cause that produces it.
When the iron core is inserted in the current carrying solenoid, the magnetic field increases due to the magnetisation of iron core and hence the flux increases.
So, the emf induced in the coil must oppose this increase in flux, so the current induced in the coil in such a direction that it will oppose the increasing magnetic field which can be done by making decrease in current. So, the current will decrease.
Q.14. Consider a metal ring kept on top of a fixed solenoid (say on a cardboard) (Fig 6.5). The centre of the ring coincides with the axis of the solenoid. If the current is suddenly switched on, the metal ring jumps up. Explain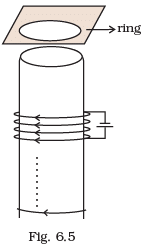
Ans. This problem is based on Lenz’s law and according to this law, the direction of induced emf or current in a circuit is such as to oppose the cause that produces it.
Initially there is no flux linked with the ring or we can say that initially flux through the ring is zero. When the switch is closed current start flowing in the circuit, magnetic flux is linked through the ring. Thus increase in flux takes place. According to Lenz’s law, this increase will be resisted and this can happen if the ring moves away from the solenoid.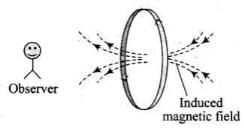 This happen because the flux increases will cause an anticlockwise current (as seen from the top in the ring in figure.), i.e., opposite direction to that in the solenoid.
This happen because the flux increases will cause an anticlockwise current (as seen from the top in the ring in figure.), i.e., opposite direction to that in the solenoid.
This makes the same sense of flow of current in the ring (when viewed from the bottom of the ring) and solenoid forming same magnetic pole in front of each other. Hence, they will repel each other and the ring will move upward.
Q.15. Consider a metal ring kept (supported by a cardboard) on top of a fixed solenoid carrying a current I (see Fig 6.5). The centre of the ring coincides with the axis of the solenoid. If the current in the solenoid is switched off, what will happen to the ring?
Ans. This problem is based on Lenz’s law and according to this law, the direction of induced emf or current in a circuit is such as to oppose the cause that produces it.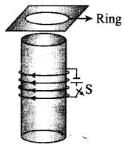
When the switch is opened, current in the circuit of solenoid stops flowing. Initially there is some magnetic flux linked with the solenoid and now if current in the circuit stops, the magnetic flux falls to zero or we can say that magnetic flux linked through the ring decreases. According to Lenz’s law, this decrease in flux will be opposed and the ring experiences downward force towards the solenoid.
This happen because the current i decrease will cause a clockwise current (as seen from the top in the ring in figure) to increase the decreasing flux. This can be done if the direction of induced magnetic field is same as that of solenoid. This makes the opposite sense of flow of current in the ring (when viewed from the bottom of the ring) and solenoid forming opposite magnetic pole in front of each other.
Hence, they will -attract each other but as ring is placed at the cardboard it could not be able to move downward.
Q.16. Consider a metallic pipe with an inner radius of 1 cm. If a cylindrical bar magnet of radius 0.8cm is dropped through the pipe, it takes more time to come down than it takes for a similar unmagnetised cylindrical iron bar dropped through the metallic pipe. Explain
Ans. Key concept: Lem’s Law.
This law gives the direction of induced emf/induced current. According to this law, the direction of induced emf or current in a circuit is such as to oppose the cause that produces it. This law is based upon the law of conservation of energy.
Eddy Current. When a changing magnetic flux is applied to a bulk piece of conducting material, then circulating currents called eddy currents are induced in the material. Because the resistance of the bulk conductor is usually low, eddy currents often have large magnitudes and heat up the conductor.
When a cylindrical bar magnet is dropped through the metallic pipe flux linked with the cylinder changes and consequently eddy currents are produced in the metallic pipe. According to Lenz’s law, these currents will oppose the motion of the magnet, which is the cause of induction.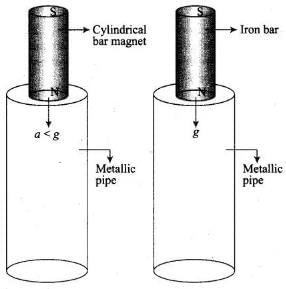
Therefore, magnet’s downward acceleration will be less than the acceleration due to gravity g. On the other hand, an un-magnetised iron bar will not produce eddy currents and will fall with acceleration due to gravity g.
Thus, the magnet will take more time to come down than it takes for a similar un-magnetised cylindrical iron bar dropped through the metallic pipe, so, magnetised magnet takes more time.
SHORT ANSWER TYPE QUESTIONS
Q.17. A magnetic field in a certain region is given by B = B0 cos (ωt)  and a coil of radius a with resistance R is placed in the x-y plane with its centre at the origin in the magnetic field (see Fig 6.6) . Find the magnitude and the direction of the current at (a, 0, 0) at t =π /2ω , t =π / ω and t = 3π /2ω .
and a coil of radius a with resistance R is placed in the x-y plane with its centre at the origin in the magnetic field (see Fig 6.6) . Find the magnitude and the direction of the current at (a, 0, 0) at t =π /2ω , t =π / ω and t = 3π /2ω .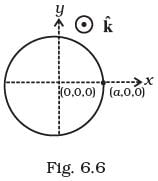 Ans. Key concept:
Ans. Key concept:
(1) First law: When ever the number of magnetic lines of force(magnetic flux) passing through a circuit changes, an emf is produced in the circuit called induced emf. The induced emf persists only as long as there is a change or cutting of flux.
(2) Second law : The induced emf is given by the rate of change of magnetic flux linked with the circuit, i.e. 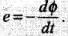 For N turns
For N turns 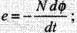 Negative sign indicates that induced emf (e) opposes the change of flux.
Negative sign indicates that induced emf (e) opposes the change of flux.
First we need to find out the flux passing through the ring at any instant and that is given by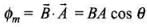
And as we know both 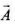 (area vector) and
(area vector) and 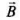 (magnetic field vector) are directed along r-axis. So, angle between them is 0.
(magnetic field vector) are directed along r-axis. So, angle between them is 0.
So, cos θ = 1 (∵ θ = 0 )
⇒ Φm = BA
Area of coil of radius a= πa2
ε = B0(πa2) cos ωt
By Faraday’s law of electromagnetic induction.
Magnitude of induced emf is given by
ε = B0(πa2) ω sin ωt
This causes flow of induced current, which is given by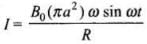
Now, the value of current at different instants,
(i) 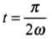
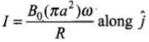
Because sin ωt = sin 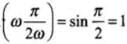
(ii) 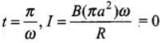
Because sin ωt = sin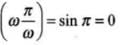
(iii) 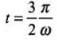
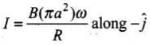
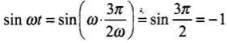
Q.18. Consider a closed loop C in a magnetic field (Fig 6.7). The flux passing through the loop is defined by choosing a surface whose edge coincides with the loop and using the formula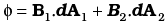 + ... . Now if we chose two different surfaces S1 and S2 having C as their edge, would we get the same answer for flux. Justify your answer.
+ ... . Now if we chose two different surfaces S1 and S2 having C as their edge, would we get the same answer for flux. Justify your answer.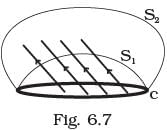 Ans. We would get the same answer for magnetic flux. Let us discuss its reason in detail. The magnetic flux linked with the surface can be considered as the number of magnetic field lines passing through the surface. So, let dФ = B.dA represents magnetic lines in an area A to B.
Ans. We would get the same answer for magnetic flux. Let us discuss its reason in detail. The magnetic flux linked with the surface can be considered as the number of magnetic field lines passing through the surface. So, let dФ = B.dA represents magnetic lines in an area A to B.
Magnetic field cannot end or start in space, this property of magnetic field lines based upon the concept of continuity. Therefore the number of lines passing through surface S1 must be the same as the number of lines passing through the surface S2. Therefore, in both the cases we get the same magnetic flux.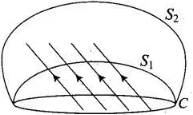
Important point: Magnetic field lines can neither be originated nor be destroyed in space. This property is based on the concept of continuity.
Q.19. Find the current in the wire for the configuration shown in Fig 6.8. Wire PQ has negligible resistance. B, the magnetic field is coming out of the paper . θ is a fixed angle made by PQ travelling smoothly over two conducting parallel wires separated by a distance d.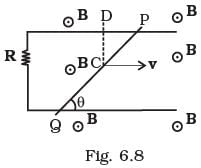 Ans. Key concept: This problem is based upon the motional emf.
Ans. Key concept: This problem is based upon the motional emf.
Consider a conducting rod of length l moving with a uniform velocity v perpendicular to a uniform magnetic field B bar, directed into the plane of the paper. Let the rod be moving to the right as shown in figure. The conducting electrons also move to the right as they are trapped within the rod.
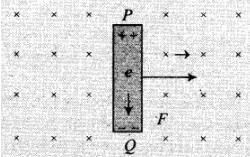 Conducting electrons experience a magnetic force Fm = evB. So they move from P to Q within the cod. The end P of the rod becomes positively charged while end Q becomes negatively charged, hence an electric field is set up within the rod which opposes the further downward movement of electrons, i.e., an equilibrium is reached and in equilibrium F, = F„, i.e.,
Conducting electrons experience a magnetic force Fm = evB. So they move from P to Q within the cod. The end P of the rod becomes positively charged while end Q becomes negatively charged, hence an electric field is set up within the rod which opposes the further downward movement of electrons, i.e., an equilibrium is reached and in equilibrium F, = F„, i.e.,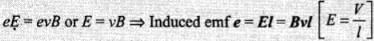
If rod is moved by making an angle θ with the direction of magnetic field or length. Induced emf,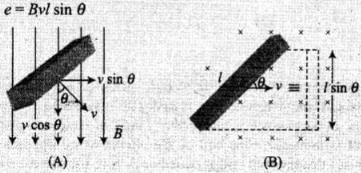 Emf induced across PQ due to its motion or change in magnetic flux linked with the loop change due to the change of enclosed area.
Emf induced across PQ due to its motion or change in magnetic flux linked with the loop change due to the change of enclosed area.
The induced electric field E along the dotted line CD (Perpendicular to both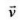 and
and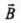 and along
and along 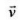 x
x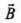 ) = vB
) = vB
Therefore, the motional emf along
PQ = (length PQ) x (field along PQ)
= (length PQ) x (vB sin θ)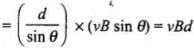
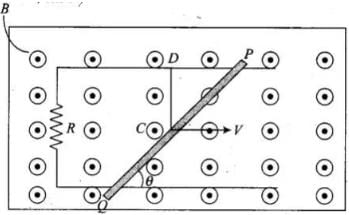
This induced emf make flow of current in closed circuit of resistance R.
Q.20. A (current vs time) graph of the current passing through a solenoid is shown in Fig 6.9. For which time is the back electromotive force (u) a maximum. If the back emf at t = 3s is e, find the back emf at t = 7 s, 15s and 40s. OA, AB and BC are straight line segments.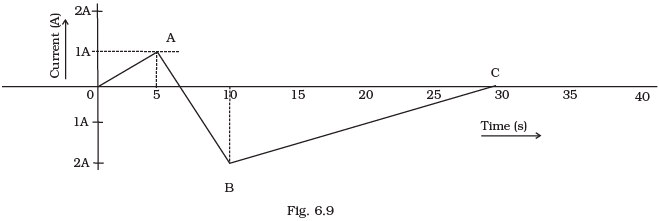
Ans. Whenever the electric current passing through a coil or circuit changes, the magnetic flux linked with it will also change. As a result of this, in accordance with Faraday's laws of electromagnetic induction, an emf is induced in the coil or the circuit which opposes the change that causes this induced emf is called back emf, the current so produced in the coil is called induced current. The induced emf is given by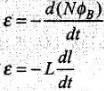 Thus, negative sign indicates that induced emf (e) opposes any change (increase or decrease) of current in the coil.
Thus, negative sign indicates that induced emf (e) opposes any change (increase or decrease) of current in the coil.
When the rate of change of current is maximum, then back emf in solenoid is («) a maximum. This occurs in AB part of the graph. So maximum back emf will be obtained between 5 s < t < 10 s.
Since, the back emf at t = 3 s is e.
Also, the rate of change of current at t = 3,
and slope(s) of OA (from t = 0 s to t = 5 s) = 1/5 A/s.
So, we have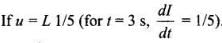
where, L is a constant (coefficient of self-induction).
And em f is ε =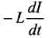
Similarly, we have for other values.
For 5 s < t < 10s, 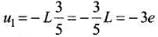
Thus, at t = 7 s, u1 = -3e
For 10 s < t <30 s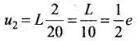
For t > 30 s, u2 = 0
Thus, the back emf at t = 7 s, 15 s are - 3e, e/2 and 0 respectively.
Q.21. There are two coils A and B separated by some distance. If a current of 2 A flows through A, a magnetic flux of 10-2 Wb passes through B (no current through B). If no current passes through A and a current of 1 A passes through B, what is the flux through A?
Ans. Let IA current is passing through coil A having mutual inductance MAB with respect to coil B.
NA=number of turns in coil A
NB= number of turns in coil B
ϕA= flux linked with coil A due to coil B
ϕB= flux linked with coil B due to coil A
MBA=Mutual inductance of coil B with respect to coil A Then
Total flux through B=MAϕA=MBAI1
10-2=MBAx2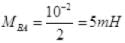
Now total flux through A=MA ϕ A=MABI2 [∵ MAB=MBA]
=5 mH x 1 Wb= 5mWb
LONG ANSWER TYPE QUESTIONS
Q.22. A magnetic field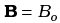 sin (ωt)
sin (ωt)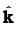 covers a large region where a wire AB slides smoothly over two parallel conductors separated by a distance d (Fig. 6.10). The wires are in the x-y plane. The wire AB (of length d) has resistance R and the parallel wires have negligible resistance. If AB is moving with velocity v, what is the current in the circuit. What is the force needed to keep the wire moving at constant velocity?
covers a large region where a wire AB slides smoothly over two parallel conductors separated by a distance d (Fig. 6.10). The wires are in the x-y plane. The wire AB (of length d) has resistance R and the parallel wires have negligible resistance. If AB is moving with velocity v, what is the current in the circuit. What is the force needed to keep the wire moving at constant velocity?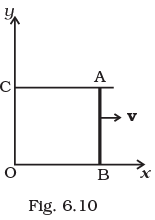 Ans. Key concept: In this problem the emf induced across AB is motional emf due to its motion, and emf induced by change in magnetic flux linked with the loop change due to change of magnetic field.
Ans. Key concept: In this problem the emf induced across AB is motional emf due to its motion, and emf induced by change in magnetic flux linked with the loop change due to change of magnetic field.
Due to motion: e = Blv
Due to change in magnetic flux: e = - N 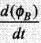
First we have to analyse the situation as shown in the figure. Let the parallel wires are at y = 0 and y = d and are placed along x-axis. Wire AB is along y-axis.
Let us redraw the diagram as shown below.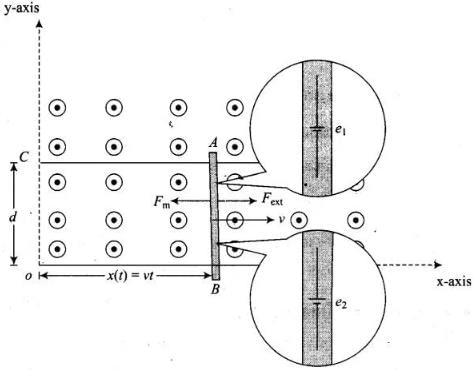 At t = 0, wire AB starts from x = 0 and moves with a velocity v. Let at time t, wire is at .t(/) = vt
At t = 0, wire AB starts from x = 0 and moves with a velocity v. Let at time t, wire is at .t(/) = vt
(where, x(t) is the displacement as a function of time).
Now, the motional emf across AB is
e1 = Blv
⇒ 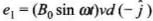
and emf due to change in field (along OABC) + the motional emf across AB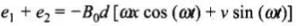
The equivalent electrical diagram is shown in the diagram below.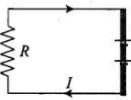 Electric current in clockwise direction is given by
Electric current in clockwise direction is given by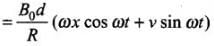
The force acting on the conductor is given by F = ilB sin 90° = HB Substituting the values,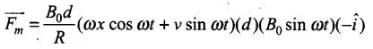
External force needed on wire is along positive x - axis to keep moving it with constant velocity is given by,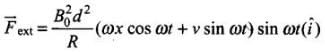
This is the required expression for force.
Q.23. A conducting wire XY of mass m and negligible resistance slides smoothly on two parallel conducting wires as shown in Fig 6.11. The closed circuit has a resistance R due to AC. AB and CD are perfect conductors. There is a magnetic field 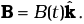
(i) Write down equation for the acceleration of the wire XY.
(ii) If B is independent of time, obtain v(t) , assuming v (0) = u0.
(iii) For (b), show that the decrease in kinetic energy of XY equals the heat lost in R.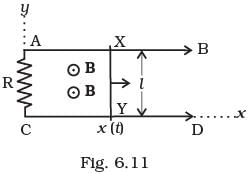 Ans. First we have to analyse the situation as shown in the figure. Let the parallel wires are at y = 0 and y = L and are placed along x-axis. Wire XY is along y-axis.
Ans. First we have to analyse the situation as shown in the figure. Let the parallel wires are at y = 0 and y = L and are placed along x-axis. Wire XY is along y-axis.
At t = 0, wire AB starts from x = 0 and moves with a velocity v. Let at time t, wire is at x(t) = vt.
(where, x(t) is the displacement as a function of time).
Let us redraw the diagram as shown below.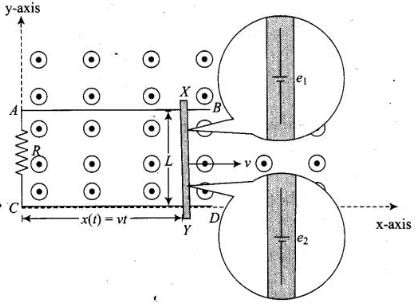
The magnetic flux linked with the loop is given by
And as we know both (area vector) and
(area vector) and  (magnetic field vector) are directed along z-axis. So angle between them is 0.
(magnetic field vector) are directed along z-axis. So angle between them is 0.
So, cos 0° = 1 (∵ θ = 0°)
⇒ 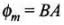
At any instant of time t,
Magnetic flux 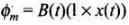
Emf induced due to change in magnetic field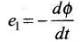
⇒ 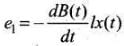
Emf induced due to motion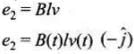
Total emf in the circuit = emf due to change in field (along XYAC) + the motional emf across XY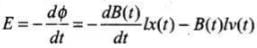
Electric current in clockwise direction (as shown in equivalent diagram) is given by
I = E/R The force acting on the conductor is given by F = ilB sin 90° = ilB Substituting the values, we have
The force acting on the conductor is given by F = ilB sin 90° = ilB Substituting the values, we have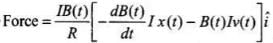
Applying Newton’s second law of motion,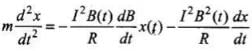 ...(i)
...(i)
which is the required equation.
If B is independent of time, i.e., B = Constant
or 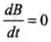
Substituting the above value in Eq (i), we have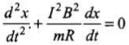
or 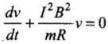
Integrating using variable separable form of differential equation, we have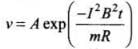
Applying given conditions, at t = 0, v = u0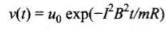
This is the required equation.
Since the power consumption is given by P = l2R
Here, 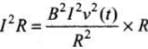
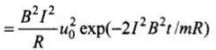
Now, energy consumed in time interval dt is given by energy consumed = Pdt = I2Rdt. Therefore, total energy consumed in time t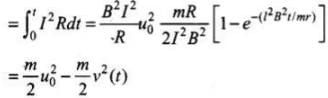
= decrease in kinetic energy.
This proves that the decrease in kinetic energy of XY equals the heat lost in R.
Q.24. ODBAC is a fixed rectangular conductor of negligible resistance (CO is not connected) and OP is a conductor which rotates clockwise with an angular velocity ω (Fig 6.12). The entire system is in a uniform magnetic field B whose direction is along the normal to the surface of the rectangular conductor ABDC. The conductor OP is in electric contact with ABDC. The rotating conductor has a resistance of λ per unit length. Find the current in the rotating conductor, as it rotates by 180°.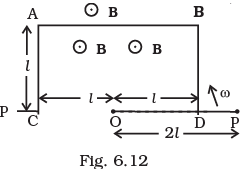 Ans. Key concept: When the conductor OP is rotated, then the rate of change of area and hence the rate of change of flux can be considered uniform from
Ans. Key concept: When the conductor OP is rotated, then the rate of change of area and hence the rate of change of flux can be considered uniform from
(i) Let us first assume the position of rotating conductor at time interval
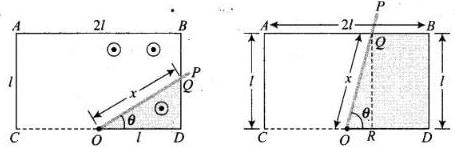 The rod OP will make contact with the side BD. Let the length OQ of the contact after some time interval t such that
The rod OP will make contact with the side BD. Let the length OQ of the contact after some time interval t such that 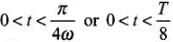 be x. The flux through the area ODQ is
be x. The flux through the area ODQ is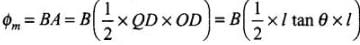
⇒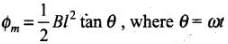
By applying Faraday’s law of EMI,
Thus, the magnitude of the cmf induced is 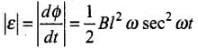
The current induced in the circuit will be 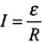 where, R is the resistance of the rod in contact.
where, R is the resistance of the rod in contact.
where, R ∝ λ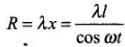
∴ 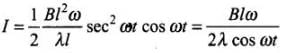
(ii) Now let the rod OP will make contact with the side AB. And the length of OQ of the contact after some time interval t such that 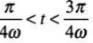 or
or 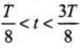 be x. The flux through the area OQBD is
be x. The flux through the area OQBD is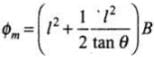
where,θ - ωt
Thus, the magnitude of emf induced in the loop is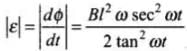
The current induced in the circuit is 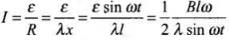
(iii) Similarly, for lime interval 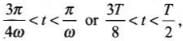 the rod will be in touch with AC.
the rod will be in touch with AC.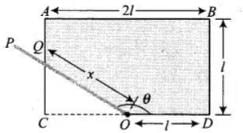
The flux through OQABD is given by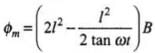
And the magnitude of emf generated in loop is given by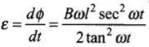
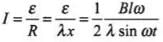
These are the required expressions.
Q.25. Consider an infinitely long wire carrying a current I (t), with 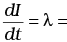 constant. Find the current produced in the rectangular loop of wire ABCD if its resistance is R (Fig. 6.13).
constant. Find the current produced in the rectangular loop of wire ABCD if its resistance is R (Fig. 6.13).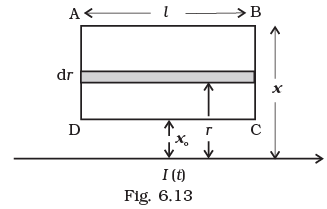 Ans. To approach these types of problems integration is very useful to find the total magnetic flux linked with the loop.
Ans. To approach these types of problems integration is very useful to find the total magnetic flux linked with the loop.
Let us first consider an elementary strip of length l and width dr at a distance r from an infinite long current carrying wire. The magnetic field at strip due to current carrying wire is given by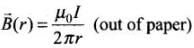
Area of elementary strip is, dA = l.dr
So, total through the loop is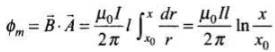 ...(i)
...(i)
The emf induced can be obtained by differentiating the eq. (i) w.r.t .t and then applying Ohm's law.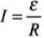
and 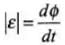
We have, induced current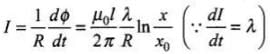
Q.26. A rectangular loop of wire ABCD is kept close to an infinitely long wire carrying a current I (t) = I0 (l - t/T) for 0 < t < T and I(0) = 0 for t > T (Fig. 6.14). Find the total charge passing through a given point in the loop, in time T. The resistance of the loop is R.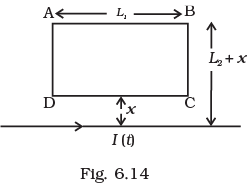 Ans. To find the charge that passes through the circuit first we have to find the relation between instantaneous current and instantaneous magnetic flux linked with it. The emf induced can be obtained by differentiating the expression of magnetic flux linked w.r.t. t and then applying Ohm’s law, we get
Ans. To find the charge that passes through the circuit first we have to find the relation between instantaneous current and instantaneous magnetic flux linked with it. The emf induced can be obtained by differentiating the expression of magnetic flux linked w.r.t. t and then applying Ohm’s law, we get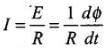
According to the problem electric current is given as a function of time.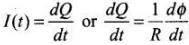
Integrating the variable separately in the form of differential equation for finding the charge Q that passed in time t, we have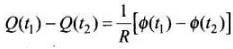

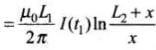
Therefore the magnitude of charge is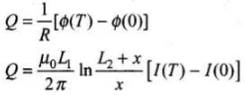
Now I(T) = 0 and I(o) = 1
∴ 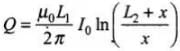
This is required expression.
Q.27. A magnetic field B is confined to a region r ≤a and points out of the paper (the z-axis), r = 0 being the centre of the circular region. A charged ring (charge = Q) of radius b, b > a and mass m lies in the x-y plane with its centre at the origin. The ring is free to rotate and is at rest. The magnetic field is brought to zero in time ∆t.
Find the angular velocity ω of the ring after the field vanishes.
Ans. Key concept: According to the law of EMI, when magnetic field changes in the circuit, then magnetic flux linked with the circuit also changes and this changing magnetic flux leads to an induced emf in the circuit. Here, magnetic field decreases which causes induced emf and hence, electric field around the ring. The torque experienced by the ring produces change in angular momentum.
As the magnetic field is brought to zero in time At, the magnetic flux linked with the ring also reduces from maximum to zero. This, in turn, induces an emf in ring as discussed above. The induces emf causes the induced electric field E around the ring.
By the relation between electric field and potential we get,
The induced emf = Electric field E x (2πb) (Because V = E x d) ...(i)
By Faraday,s law od EMI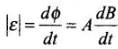
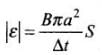
From Eqs. (i) and (ii), We have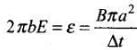
As we know the electric force experienced by the charged ring, Fe = QE
This force try to rotate the coil, and the torque is given by
Torque = b x Force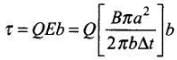
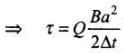
If ΔL is the change in angular momentum,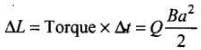
Since, initial angular momentum = 0
And Torque x Δt = Change in angular momentum
Final angular momentum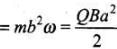
Where, mb2 = I (moment of inertia of ring)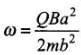
On rearranging the terms, we have the required expression of angular speed.
Q.28. A rod of mass m and resistance R slides smoothly over two parallel perfectly conducting wires kept sloping at an angle θ with respect to the horizontal (Fig. 6.15). The circuit is closed through a perfect conductor at the top. There is a constant magnetic field B along the vertical direction. If the rod is initially at rest, find the velocity of the rod as a function of time.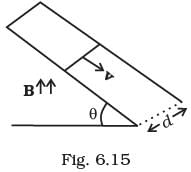 Ans. Let us first divide the magnetic field in the components one is along the inclined plane = B sin θ and other component of magnetic field is perpendicular the plane =B cos θ
Ans. Let us first divide the magnetic field in the components one is along the inclined plane = B sin θ and other component of magnetic field is perpendicular the plane =B cos θ
Now, the conductor moves with speed v perpendicular to B cos θ, component of magnetic field. This causes motional emf across two ends of rod, which is
given by = v(B cos θ)d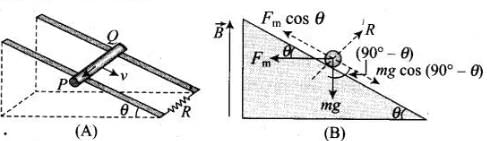 This makes flow of induced current
This makes flow of induced current 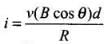 where R is the resistance of rod. Now, current carrying rod experience a magnetic force which is given by Fm = iBd (horizontally in backward direction). Now, the component o f magnetic force parallel to the inclined p lane along upward direction
where R is the resistance of rod. Now, current carrying rod experience a magnetic force which is given by Fm = iBd (horizontally in backward direction). Now, the component o f magnetic force parallel to the inclined p lane along upward direction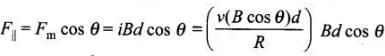
where, 
Also, the component of weight (mg) parallel to inclined plane along downward direction = mg sin θ.
Now, by Newton's second law of motion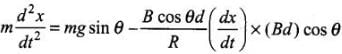
⇒ 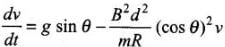
⇒ 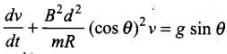
But, this is the linear differential equation.
On solving, we get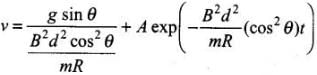
A is a constant to be determined by initial conditions.
The required expression of velocity as a function of time is given by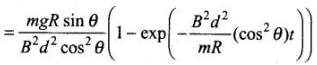
Q.29. Find the current in the sliding rod AB (resistance = R) for the arrangement shown in Fig 6.16. B is constant and is out of the paper. Parallel wires have no resistance. v is constant. Switch S is closed at time t = 0.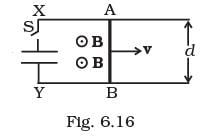 Ans. This is the similar problem as we discussed above. Here, a conductor of length d moves with speed v, perpendicular to the magnetic field B as shown in figure. Due to this a motional emf is induced across two ends of rod (e = vBd). Since, switch S is closed at time t = 0, capacitor is charged by this potential difference. Let Q(t) be the charge on the capacitor and current flows from A to B.
Ans. This is the similar problem as we discussed above. Here, a conductor of length d moves with speed v, perpendicular to the magnetic field B as shown in figure. Due to this a motional emf is induced across two ends of rod (e = vBd). Since, switch S is closed at time t = 0, capacitor is charged by this potential difference. Let Q(t) be the charge on the capacitor and current flows from A to B.
Now, the induced current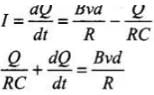
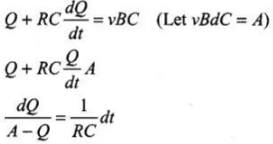
By integrating we have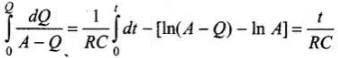
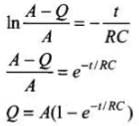
Current in the rod,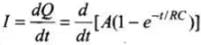
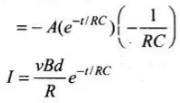
Q.30. Find the current in the sliding rod AB (resistance = R) for the arrangement shown in Fig 6.17. B is constant and is out of the paper. Parallel wires have no resistance. v is constant. Switch S is closed at time t = 0.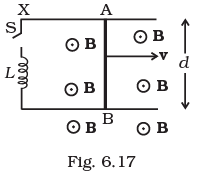 Ans. This is the similar problem as we discussed above. Here, a conductor of length d moves with speed v, perpendicular to magnetic field B as shown in figure. Due to this an motional emf is induced across two ends of rod (e = vBd). Since, switch S is closed at time t = 0. current start growing in inductor by the potential difference due to motional emf.
Ans. This is the similar problem as we discussed above. Here, a conductor of length d moves with speed v, perpendicular to magnetic field B as shown in figure. Due to this an motional emf is induced across two ends of rod (e = vBd). Since, switch S is closed at time t = 0. current start growing in inductor by the potential difference due to motional emf.
By applying KVL in the given circuit, we have
This is linear differential equation. On solving, we get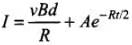
At t = 0, I = 0
⇒ 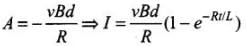
This is the required expression of current.
Q.31. A metallic ring of mass m and radius l (ring being horizontal) is falling under gravity in a region having a magnetic field. If z is the vertical direction, the z-component of magnetic field is Bz = Bo (1+λ z). If R is the resistance of the ring and if the ring falls with a velocity v, find the energy lost in the resistance. If the ring has reached a constant velocity, use the conservation of energy to determine v in terms of m , B, λ and acceleration due to gravity g.
Ans. In this problem a relation is established between induced current, power lost and velocity acquired by freely falling ring.
The magnetic flux linked with the metallic ring of mass m and radius l ring being horizontal falling under gravity in a region having a magnetic field whose z-component of magnetic field is Bz = B0(1 + λz) is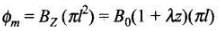
Applying Faraday’s law of EMI, we have emf induced given by 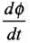 = rate of change of flux. Also, by Ohm’s law
= rate of change of flux. Also, by Ohm’s law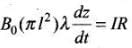
We have 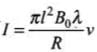
Energy lost/ second = 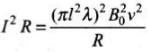
Rate of change of PE = 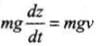 [as kinetic energy is constant for v = constant]
[as kinetic energy is constant for v = constant]
According to the law of conservation of energy
Thus, 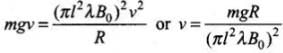
This is the required expression of velocity.
Q.32. A long solenoid ‘S’ has ‘n’ turns per meter, with diameter ‘a’. At the centre of this coil we place a smaller coil of ‘N’ turns and diameter ‘b’ (where b < a). If the current in the solenoid increases linearly, with time, what is the induced emf appearing in the smaller coil.
Plot graph showing nature of variation in emf, if current varies as a function of mt2 + C.
Ans. Magnetic field due to a solenoid is given by, B = μ0ni where signs are as usual.
In this problem the current is varying with time. Due to this an emf is induced in the coil of radius b.
Magnetic flux in smaller coil is
ϕm = NBA
where, A = πb2
Applying Faraday's law of EMI, we have
So, 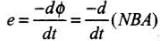
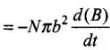
where, B = μ0Ni
⇒ 
 Since, current varies as a function of time, so
Since, current varies as a function of time, so
i(t) = mt2 + c
⇒ 
By solving this equation we get, e =
Negative sign signifies opposite nature of induced emf. The magnitude of emf varies with time as shown in figure.
|
74 videos|314 docs|88 tests
|
FAQs on NCERT Exemplar: Electromagnetic Induction - Physics Class 12 - NEET
| 1. What is electromagnetic induction? |  |
| 2. How does electromagnetic induction work? |  |
| 3. What are the applications of electromagnetic induction? |  |
| 4. How does a generator work based on electromagnetic induction? |  |
| 5. Can you explain the concept of mutual induction? |  |
















