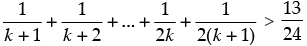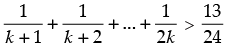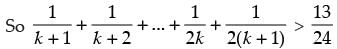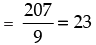Q.1. Give an example of a statement P(n) which is true for all n ≥ 4 but P(1), P(2) and P(3) are not true. Justify your answer.
Ans.
The required statement is P(n) = 2n < n!
Justification: P(n) : 2n < n!
P(1) : 2.1 < 1!
⇒ 2 < 1 not true
P(2) : 2.2 < 2!
⇒ 4 < 2.1
⇒ 4 < 2 not true
P(3) : 2.3 < 3!
⇒ 6 < 3.2.1
⇒ 6 < 6 not true
P(4) : 2.4 < 4!
⇒ 8 < 4.3.2.1
⇒ 8 < 24 True
P(5) : 2.5 < 5!
⇒ 10 < 5.4.3.2.1
⇒ 10 < 120 True
Hence, P(n) = 2n < n! is not true for P(1), P(2) and P(3) but it is true for all values of n ≥ 4.
Q.2. Give an example of a statement P(n) which is true for all n. Justify your answer.
Prove each of the statements in Exercises 3 - 16 by the Principle of Mathematical Induction :
Ans.
The required statement is
P(n) : 1 + 2 + 3 + ... + n =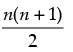
Justification: P(1) : 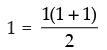
P(k) : 1 + 2 + 3 + ... + k =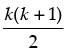 Let it be true.
Let it be true.
P(k + 1) : 1 + 2 + 3 + ... + k + (k + 1)
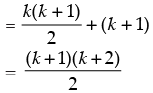
Hence, P(k + 1) is true whenever P(k) is true.
Therefore by the principle of mathematical induction we have p(n) is true for all n.
Q.3. 4n – 1 is divisible by 3, for each natural number n.
Ans.
Let P(n) : 4n – 1
Step 1: P(1) = 4 – 1 = 3 which is divisible by 3, so it is true.
Step 2: P(2) = 4k – 1 = 3λ . Let it be true.
Step 3: P(k + 1) = 4k + 1 – 1
= 4k .4 – 1 = 4.4k – 4 + 3 = 4(4k – 1) + 3
= 4 (3λ) + 3 (from Step 2)
= 3[4λ + 1] which is true as it is divisible by 3.
Hence, P(k + 1) is true whenever P(k) is true.
Q.4. 23n – 1 is divisible by 7, for all natural numbers n.
Ans.
Let P(n) : 23n – 1
Step 1: P(1) = 23.1 – 1 = 8 – 1 = 7 which is divisible by 7.
So, P(1) is true.
Step 2: P(k) = 23k – 1 = 7l. Let it be true.
Step 3: P(k + 1) = 23(k + 1) – 1
= 23k + 3 – 1 = 23.23k – 8 + 7 = 8.23k – 8 + 7
= 8(23k – 1) + 7 (from Step 2)
= 8.7λ + 7
= 7(8λ + 1) which is true as it is divisible by 7
Hence, P(k + 1) is true whenever P(k) is true.
Q.5. n3 – 7n + 3 is divisible by 3, for all natural numbers n.
Ans.
Let P(n) : n3 – 7n + 3
Step 1: P(1) : (1)3 – 7(1) + 3
= 1 – 7 + 3 = - 3 which is divisible by 3.
So, P(1) is true .
Step 2: Assume P(k) is true for some K∈N P(k) : k3 – 7k + 3 = 3λ, λ∈N.
⇒ k3 = 3λ + 7k – 3..............(i)
Step 3: Now we have to prove P(k + 1) : (k + 1)3 – 7(k + 1) + 3 is divisible by 3.
Now P(k + 1) : (k + 1)3 – 7(k + 1) + 3= k3 + 1 + 3k2 + 3k – 7k – 7 + 3
= k3 + 3k2 – 4k – 3
= (3λ + 7k – 3) + 3k2 – 4k – 3 (using equation (i))
= 3k2 + 3k + 3λ – 6
= 3(k2 + k + λ – 2) is divisible by 3.
⇒ P(k + 1) is true.
Hence, P(k + 1) is true whenever P(k) is true.
Therefore by the principle of mathematical induction we have p(n) is true for all n.
Q.6. 32n – 1 is divisible by 8, for all natural numbers n.
Ans.
Let P(n) : 32n – 1
Step 1: P(1) : 32 – 1 = 9 – 1 = 8 which is divisible by 8.
So, P(1) is true.
Step 2: Assume P(k) is true for some P(k) : 32k – 1 = 8λ, λ∈N. Step 3: Now we have to prove P(k + 1) : 32(k + 1) – 1 is divisible by 8.
P(k + 1) : 32(k + 1) – 1
= 32k + 2 – 1 = 32.32k – 9 + 8 = 9(32k – 1) + 8
= 9.8λ + 8 (from Step 2)
= 8[9λ + 1] is divisible by 8.
⇒ P(k + 1) is true.
Hence, P(k + 1) is true whenever P(k) is true.
Therefore by the principle of mathematical induction we have p(n) is true for all n.
Q.7. For any natural number n, 7n – 2n is divisible by 5.
Ans.
Let P(n) : 7n – 2n
Step 1: P(1) : 71 – 21 = 5 which is divisible by 5.
So it is true for P(1).
Step 2: P(k) : 7k – 2k = 5λ. Let it be true for P(k).
Step 3: P(k +1) = 7k + 1 – 2k + 1
= 7k + 1 + 7k.2 – 7k.2 – 2k + 1
= (7k + 1 – 7k.2) + 7k.2 – 2k + 1)
= 7k(7 – 2) + 2.(7k – 2k)
= 5.7k + 2.5λ (from Step 2)
= 5(7k + 2λ) which is divisible by 5.
So, it is true for P(k + 1).
Hence, P(k + 1) is true whenever P(k) is true.
Q.8. For any natural number n, xn – yn is divisible by x – y, where x and y are any integers with x ≠ y.
Ans.
Let P(n) : xn – yn
Step 1: P(1) : x1 – y1 = x – y which is divisible by x – y.
So P(1) is true.
Step 2: P(k) : xk – yk = (x – y)λ. Let it be true.
Step 3: P(k + 1) = xk + 1 – yk + 1 = xk + 1 – xky – xky – yk + 1
= (xk + 1 – xky) + (xky – yk + 1)
= xk(x – y) + y(xk – yk)
= xk (x – y) + y.(x – y)λ (from Step 2)
= (x – y) (xk + yλ)which is divisible by (x – y).
So, it is true for P(k + 1).
Q.9. n3 – n is divisible by 6, for each natural number n ≥ 2.
Ans.
Let P(n) : n3 – n
Step 1: P(2) : 23 – 2 = 6 which is divisible by 6. So it is true for P(2).
Step 2: P(k) : k3 – k = 6λ. Let it be true for k ≥ 2
⇒ k3 = 6λ + k ...(i)
Step 3: P(k + 1)
= (k + 1)3 – (k + 1)
= k3 + 1 + 3k2 + 3k – k – 1
= k3 – k + 3(k2 + k)
= 6λ + 3(k2 + k) [from (i)]
We know that 3(k2 + k) is divisible by 6 for every value of k ∈ N.
Hence P(k + 1) is true whenever P(k) is true.
Q.10. n (n2 + 5) is divisible by 6, for each natural number n.
Ans.
Let P(n) : n(n2 + 5)
Step 1: P(1) : 1(1 + 5) = 6 which is divisible by 6. So it is true for P(1).
Step 2: P(k) : k(k2 + 5) = 6λ. Let it be true
⇒ k3 + 5k = 6λ
⇒ k3 = 6λ – 5k ...(i)
Step 3: P(k + 1) = (k + 1)[(k + 1)2 + 5]
= (k + 1)[k2 + 1 + 2k + 5]
= (k + 1)[k2 + 2k + 6]
= k3 + 2k2 + 6k + k2 + 2k + 6
= k3 + 3k2 + 8k + 6
= k3 + 5k + 3k2 + 3k + 6
= 6λ – 5k + 5k + 3(k2 + k + 2) [From (i)]
= 6λ + 3(k2 + k + 2)
We know that k2 + k + 2 is divisible by 2 for each value of k ∈ N,
so, let k2 + k + 2 = 2m.
So P(k + 1) = 6λ + 3.2m = 6(λ + m) which is divisible by 6.
Hence, P(k + 1) is true whenever P(k) is true.
Q.11. n2 < 2n for all natural numbers n ≥ 5.
Ans.
Let P(n) : n2 < 2n for all natural number, n ≥ 5.
Step 1: P(5) : 52 < 25 ⇒ 25 < 32 which is true. So P(5) is true.
Step 2: Assume P(k) is true for some k∈N, k ≥ 5 ⇒ P(k) : k2 < 2k.............(i) is true.
Step 3: Now we have to prove P(k + 1) : (k + 1)2 < 2k + 1 is true where k ≥ 5.
Now we have (k + 1)2 = k2 + 2k + 1 < 2k + 2k + 1 .............(ii) [using equation(i)]
Now let 2k + 2k + 1 < 2k + 1
⇒ 2k + 2k + 1 < 2k . 2 = 2k + 2k
⇒ (2k + 1) < 2k which is true for K∈N , k ≥ 5 ….........(iii)
So (k + 1)2 < 2k + 2k [using (ii) and (iii)]
⇒ (k + 1)2 < 2.2k
⇒(k + 1)2 < 2k + 1.
⇒ P(k + 1) is true.
Hence, P(k + 1) is true whenever P(k) is true.
Therefore by the principle of mathematical induction we have p(n) is true for all n ≥ 5.
Q.12. 2n < (n + 2)! for all natural number n
Ans.
Let p(n) : 2n < (n + 2)! for all natural number n.
Step 1: P(1): 2.1 < (1 + 2)!
⇒ 2 < 3! ⇒ 2 < 6 which is true (∴ 3! = 3 × 2 × 1 = 6)
So P(1) is true.
Step 2: Assume P(k) is true for some K∈N ⇒ P(k): 2k < (k + 2)! is true..
Step 3: Now we have to prove P(k + 1) : 2(k + 1) < (k + 1 + 2)! is true.
Since 2k < (k + 2)! (from Step 2)
⇒ 2k + 2 < (k + 2)! + 2
⇒ 2(k + 1) < (k + 2)! + 2............(i)
Now let (k + 2)! + 2 < (k + 3)!............(ii)
⇒ 2 < (k + 3)! - (k + 2)!
⇒2 < (k + 2)! [k + 3-1]
2 < (k + 2)!.(k + 2) which is true for any natural number k.
∴ 2(k + 1) < (k + 3)! [using (i) and (ii)]
⇒ 2(k + 1) < (k + 2 + 1)!
⇒ P(k + 1) is true.
Hence, P(k + 1) is true whenever P(k) is true. Therefore by the principle of mathematical induction we have p(n) is true for all n.
Q.13. 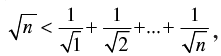 for all natural numbers n ≥ 2.
for all natural numbers n ≥ 2.
Ans.
Let P(n) 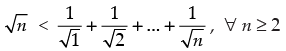
Step 1: P(2) :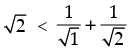 which is true.
which is true.
Step 2: P(k) 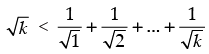 Let it be true.
Let it be true.
Step 3: P(k + 1) :
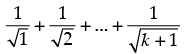
From Step 2, we have
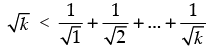
⇒ 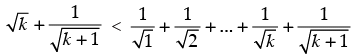
⇒ 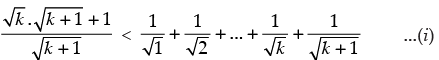
Now if
⇒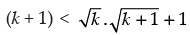
⇒ 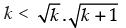 ...(ii)
...(ii)
From eqn. (i) and (ii) we get
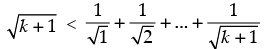
Hence, P(k +1) is true whenever P(k) is true.
Q.14. 2 + 4 + 6 + ... + 2n = n2 + n for all natural numbers n.
Ans.
Let P(n) : 2 + 4 + 6 + ... + 2n = n2 + n, ∀n ∈ N
Step 1: P(1) : 2 = 12 + 1 = 2
which is true for P(1)
Step 2: P(k) : 2 + 4 + 6 + ...+ 2k = k2 + k. Let it be true.
Step 3: P(k + 1) : 2 + 4 + 6 +...+ 2k + 2k + 2
= k2 + k + 2k + 2
= k2 + 3k + 2
= k2 + 2k + k + 1 + 1
= (k + 1)2 + (k + 1)
Which is true for P(k + 1)
So, P(k + 1) is true whenever P(k) is true.
Q.15. 1 + 2 + 22 + ... + 2n = 2n+1 – 1 for all natural numbers n.
Ans.
Let P(n) : 1 + 2 + 22 + … + 2n = 2n + 1 – 1, n∈N.
P(n) : 20 + 21 + 22 + … + 2n = 2n+1 – 1
Step 1: P(1) L.H.S = 20 +21 = 1 + 2 = 3.
R.H.S = 21 + 1 – 1 = 22 – 1 = 4 – 1 = 3 .
L.H.S = R.H.S. So P(1) is true.
Step 2: Assume P(k) is true for some k∈N
⇒ P(k) : 20 + 21 + 22 + … + 2k = 2k + 1 – 1..........(i)
Step 3: Now we have to prove P(k + 1) : 20 + 21 + 22 +…+ 2k + 2k + 1 = 2(k + 1) + 1 – 1.
Adding 2k + 1 on both sides of equation (i)
20 + 21 + 22 + … + 2k + 2k + 1
= 2k + 1 – 1 + 2k + 1 = 2.2k + 1 – 1
= 2k + 2 – 1
= 2(k + 1) + 1 – 1
⇒ P(k + 1) is true.
Q.16. 1 + 5 + 9 + ... + (4n – 3) = n (2n – 1) for all natural numbers n.
Ans.
Let P(n) : 1 + 5 + 9 + … + (4n – 3) = n(2n – 1), ∀ n ∈ N
Step 1: P(1) : 1 = 1(2.1 – 1) = 1 which is true for P(1)
Step 2: P(k) : 1 + 5 + 9 +...+ (4k – 3) = k(2k – 1). Let it be true.
Step 3: P(k + 1) : 1 + 5 + 9 +...+ (4k – 3) + (4k + 1)
= k(2k – 1) + (4k + 1) = 2k2 – k + 4k + 1
= 2k2 + 3k + 1 = 2k2 + 2k + k + 1
= 2k(k + 1) + 1(k + 1) = (2k + 1)(k + 1)
= (k + 1)(2k + 2 – 1) = (k + 1) [2(k + 1) – 1]
Which is true for P(k + 1).
Hence, P(k + 1) is true whenever P(k) is true.
Long Answer Type
Q.17. A sequence a1, a2, a3 ... is defined by letting a1 = 3 and ak = 7ak–1 for all natural numbers k ≥ 2. Show that an = 3.7n–1 for all natural numbers.
Ans.
Given that:
a1 = 3
a2 = 7a2 – 1 = 7.a1 = 7.3 = 21
a3 = 7.a3 – 1 = 7.a2 = 7.21 = 147...
Let P(n) : an = 3.7n – 1, ∀n∈N
Step 1: P(2): a2 = 3.72 – 1 = 21 ⇒ 21. So P(2) is true.
Step 2: P(k): ak = 3.7k – 1. Let it be true.
Step 3: ak = 7ak – 1 (given)
Put k = k + 1
ak + 1 = 7ak = 7(3.7k – 1) = 3.7k + 1 – 1 = 3.7(k + 1) – 1
which is true for P(k + 1)
Hence, P(k + 1) is true whenever P(k) is true.
Q.18. A sequence b0, b1, b2 ... is defined by letting b0 = 5 and bk = 4 + bk – 1 for all natural numbers k. Show that bn = 5 + 4n for all natural number n using mathematical induction.
Ans.
We have b0 = 5 and bk = 4 + bk – 1
⇒b0 = 5, b1 = 4 + b0 = 4 + 5 = 9 and b2 = 4 + b1 = 4 + 9 = 13
Let P(n) : bn = 5 + 4n
Step 1: P(1) : b1 = 5 + 4 = 9 ⇒ 9 = 9 which is true.
Step 2: Assume P(k) is true for some k∈N ⇒ P(k): bk = 5 + 4k is true..
Step 3: Given that:
P(k) = 4 + bk – 1
⇒ P(k + 1) = 4 + bk + 1 – 1
⇒ P(k + 1) = 4 + bk = 4 + 5 + 4k
⇒ P(k + 1) = 5 + 4(k + 1) which is true for P(k + 1)
Hence, P(k + 1) is true whenever P(k) is true.
Q.19. A sequence d1, d2, d3 ... is defined by letting d1 = 2 and dk =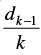
for all natural numbers, k ≥ 2. Show that dn =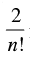 for all n ∈ N.
for all n ∈ N.
Ans.
Given that: d1 = 2 and dk =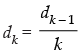
Let P(n) :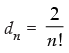
Step 1: P(1) :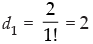 which is true for P(1).
which is true for P(1).
Step 2: P(k) :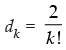 Let it be true for P(k).
Let it be true for P(k).
Step 3: Given that: dk =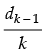
∴ 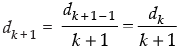
⇒ 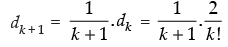
⇒ 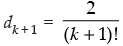 Which is true for P(k + 1)
Which is true for P(k + 1)
Hence, P(k + 1) is true whenever P(k) is true.
Q.20. Prove that for all n ∈ N
cos α + cos (α + β) + cos (α + 2β) + ... + cos (α + (n – 1) β)
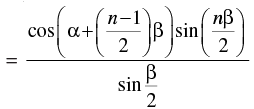
Ans.
Let P(n) : cos a + cos (a + b) + cos (a + 2b) + ... + cos [a + (n – 1)b]
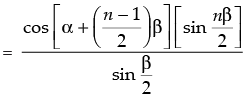
Step 1: P(1) :cos α =
which is true for P(1)
Step 2: P(k) : cos α + cos (α +β) + cos (α + 2β) + ... + cos [α + (k – 1)β]
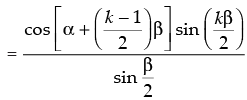 Let it be true.
Let it be true.
Step 3: P(k + 1) : cos α + cos (α + b) + cos (α + 2b) + ... + cos [α + (k – 1)b]
+ cos [ α + (k + 1 – 1)b]
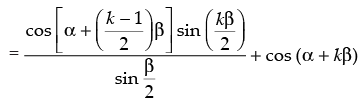
(from Step 2)
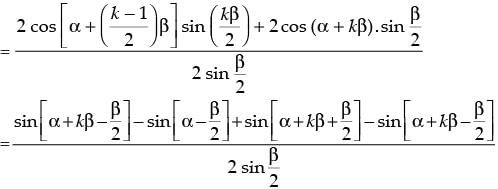
[∴ 2 cos A sin B = sin (A + B) – sin (A – B)]
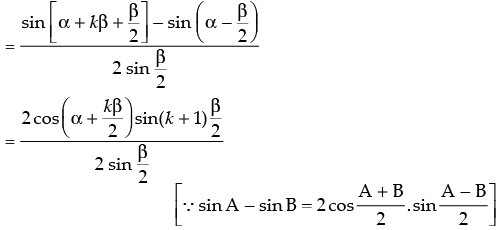
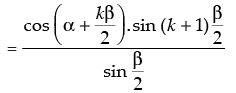
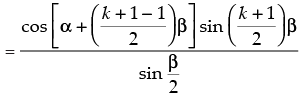 which is true for P(k + 1)
which is true for P(k + 1)
Hence, P(k + 1) is true whenever P(k) is true.
Q.21. Prove that, cos θ cos 2θ cos22θ ... cos2n–1θ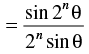 for all n ∈ N.
for all n ∈ N.
Ans.
Let P(n) : cos θ.cos 2θ.cos 22θ…cos 2n – 1θ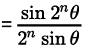 ,∀n ∈ N.
,∀n ∈ N.
Step 1: P(1) :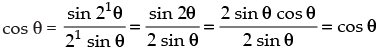
⇒ cos θ = cos θ which is true for P(1)
Step 2: P(k) : cos θ.cos 2θ.cos 22θ ... cos 2k – 1 θ =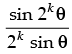
Let it be true for P(k).
Step 3: P(k + 1) : cos θ.cos 2θ.cos 22θ ... cos 2k – 1θ. cos 2(k + 1) – 1θ
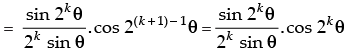
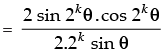
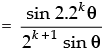 [∵ 2 sin θ cos θ = sin 2θ]
[∵ 2 sin θ cos θ = sin 2θ]
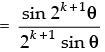 which is true for P(k + 1).
which is true for P(k + 1).
Hence, P(k + 1) is true whenever P(k) is true.
Q.22. Prove that, sin θ + sin 2θ + sin 3θ + ... + sin nθ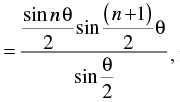
for all n ∈ N.
Ans.
Let p(n) : sin θ + sin 2θ + sin 3θ + … + sin nθ
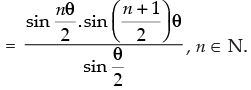
Step 1: P(1) : sin θ =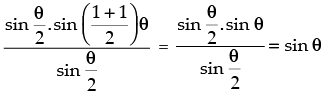
∴ sin θ = sin θ which is true for P(1).
Step 2: P(k) : sin θ + sin 2θ + sin 3θ + ... + sin kθ
 . Let it be true for P(k).
. Let it be true for P(k).
Step 3: P(k + 1) : sin θ + sin 2θ + sin 3θ + ... + sin (k + 1)θ
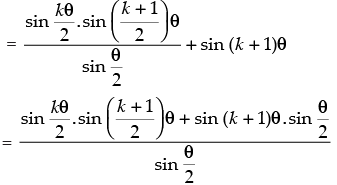

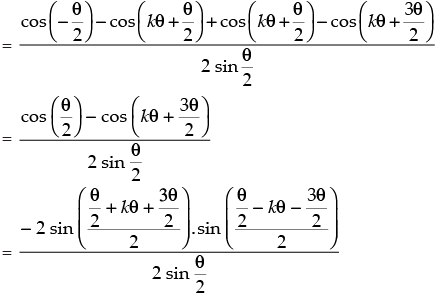
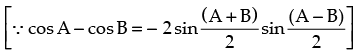
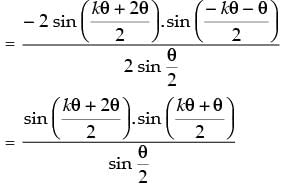
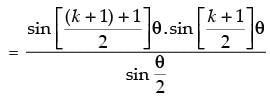 which is true for P(k + 1).
which is true for P(k + 1).
Hence, P(k + 1) is true whenever P(k) is true.
Q.23. Show that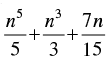 is a natural number for all n ∈ N.
is a natural number for all n ∈ N.
Ans.
Let P(n) : 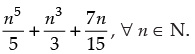
Step 1: P(1) : 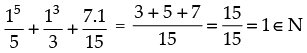
Which is true for P(1).
Step 2: P(k) 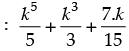 . Let it be true for P(k) and let
. Let it be true for P(k) and let
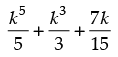 =λ
=λ
Step 3: P(k + 1) =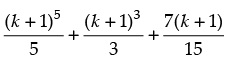
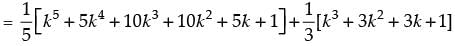
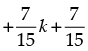
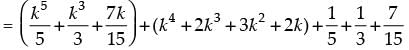
= λ + k4 + 2k3 + 3k2 + 2k + 1 [from Step 2]
= positive integers = natural number
Which is true for P(k + 1).
Hence, P(k + 1) is true whenever P(k) is true.
Q.24. Prove that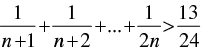 , for all natural numbers n > 1.
, for all natural numbers n > 1.
Ans.
Let P(n) : 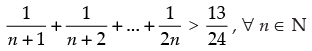
Step 1: P(2) : 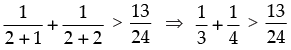
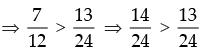 which is true for P(2).
which is true for P(2).
Step 2: P(k) :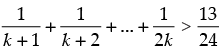 .Let it be true for P(k).
.Let it be true for P(k).
Step 3: P(k + 1) :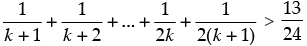
Since 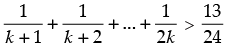
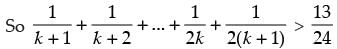
Which is true for P(k + 1).
Hence, P(k + 1) is true whenever P(k) is true.
Q.25. Prove that number of subsets of a set containing n distinct elements is
2n, for all n ∈ N.
Ans.
Let P(n) : Number of subsets of a set containing n distinct
elements is 2n, ∀ n ∈ N
Step 1: It is clear that P(1) is true for n = 1. Number of subsets
= 21 = 2. Which is true.
Step 2: P(k) is assumed to be true for n = k. Since the number of subsets = 2k.
Step 3: P(k + 1) = 2k + 1
We know that if one number (i.e., element) is added to the elements of a given set,
the number of subsets become double.
∴ Number of subsets of set having (k + 1) distinct elements
= 2 x 2k = 2k + 1 which is true for P(k + 1).
Hence P(k + 1) is true
whenever P(k) is true.
Objective Type Questions
Q.26. If 10n + 3.4n+2 + k is divisible by 9 for all n ∈ N,
then the least positive integral value of k is
(A) 5
(B) 3
(C) 7
(D) 1
Ans.
Let P(n) = 10n + 3.4n + 2 + k is divisible by 9, ∀ n ∈ N
P(1) = 101 + 3.41 + 2 + k = 10 + 3.64 + k
= 10 + 192 + k = 202 + k must be divisible by 9.
If (202 + k) is divisible by 9 then k must be equal to 5
202 + 5 = 207 which is divisible by 9
So, the least positive integral value of k = 5.
Hence, the correct option is (a).
Q.27. For all n ∈ N, 3.52n+1 + 23n+1 is divisible by
(A) 19
(B) 17
(C) 23
(D) 25
Ans.
Let P(n) : 3.52n + 1 + 23n + 1
For P(1) : 3.52.1 + 1 + 23.1 + 1 = 3.53 + 24 = 3(125) + 16 = 375 + 16
= 391 = 23 x 17
So it is divisible by 17 and 23 both.
Hence, the correct option is (b) and (c).
Q.28. If xn – 1 is divisible by x – k, then the least positive integral value of k is (A) 1
(B) 2
(C) 3
(D) 4
Ans.
Let P(n) = xn – 1 is divisible by x – k.
P(1) = x – 1 is divisible by x – k.
Since k = 1 is the possible least integral value of k.
Hence, the correct option is (a).
Fill in the Blanks
Q.29. If P(n) : 2n < n!, n ∈ N, then P(n) is true for all n ≥ ________.
Ans.
Given that P(n) : 2n < n!, ∀ n ∈ N
For n = 1 , 2 < 1 (Not true)
For n = 2 , 2 × 2 < 2! ⇒ 4 < 2 (Not true) For n = 3 , 2 × 3 < 3! ⇒ 6 < 3.2.1 ⇒ 6 < 6 (Not true) For n = 4 , 2 × 4 < 4! ⇒ 8 < 4.3.2.1 ⇒ 8 < 24 (true)
For n = 5 , 2 × 5 < 5! ⇒ 10 < 5.4.3.2.1 ⇒10 < 120(true)
So, P(n) is true for n ≥ 4.
Hence, the value of the filler is 4.
State whether the following statement is true or false. Justify.
Q.30. Let P(n) be a statement and let P(k) ⇒ P(k + 1), for some natural number k, then P(n) is true for all n ∈ N.
Ans.
Given that: P(k) ⇒ P(k + 1)
P(1)⇒ P(2) which is not true.
Hence, the statement is ‘False’.
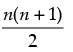
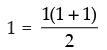
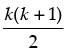 Let it be true.
Let it be true.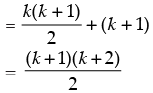
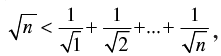 for all natural numbers n ≥ 2.
for all natural numbers n ≥ 2.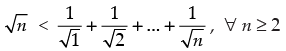
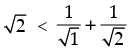 which is true.
which is true.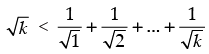 Let it be true.
Let it be true.
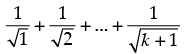
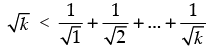
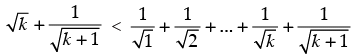
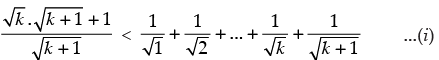

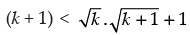
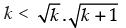 ...(ii)
...(ii)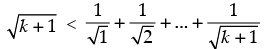
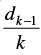
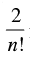 for all n ∈ N.
for all n ∈ N.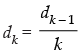
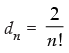
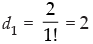 which is true for P(1).
which is true for P(1).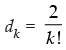 Let it be true for P(k).
Let it be true for P(k).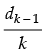
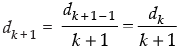
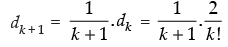
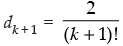 Which is true for P(k + 1)
Which is true for P(k + 1)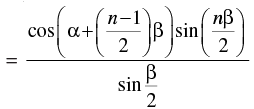
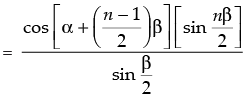

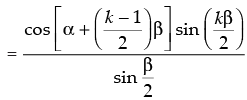 Let it be true.
Let it be true.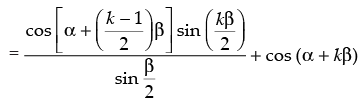
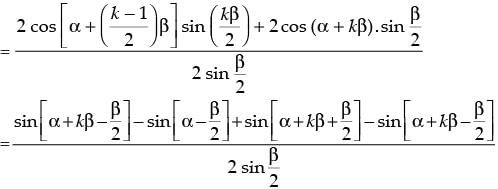
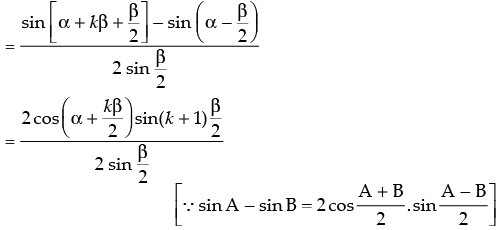
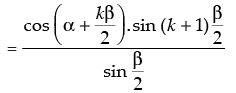
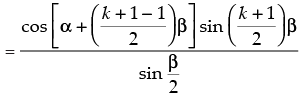 which is true for P(k + 1)
which is true for P(k + 1)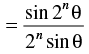 for all n ∈ N.
for all n ∈ N.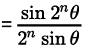 ,∀n ∈ N.
,∀n ∈ N.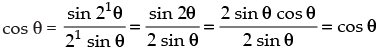
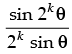
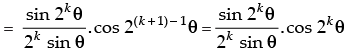
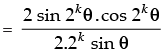
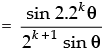 [∵ 2 sin θ cos θ = sin 2θ]
[∵ 2 sin θ cos θ = sin 2θ]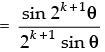 which is true for P(k + 1).
which is true for P(k + 1).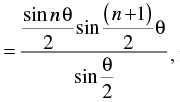
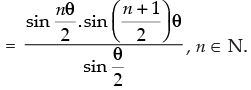
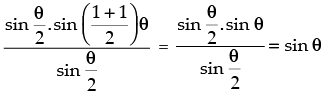
 . Let it be true for P(k).
. Let it be true for P(k).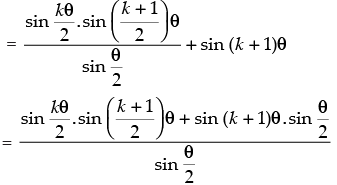

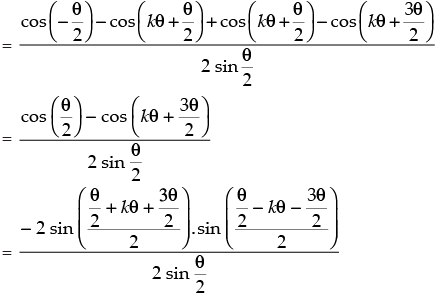
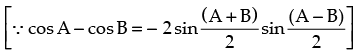
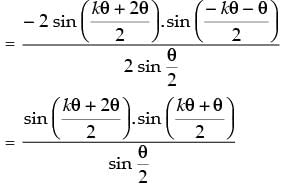
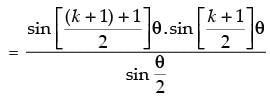 which is true for P(k + 1).
which is true for P(k + 1).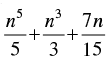 is a natural number for all n ∈ N.
is a natural number for all n ∈ N.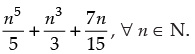
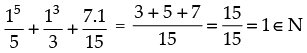
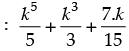 . Let it be true for P(k) and let
. Let it be true for P(k) and let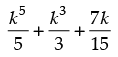 =λ
=λ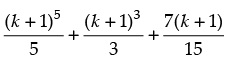
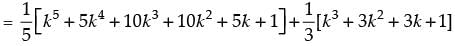
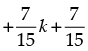
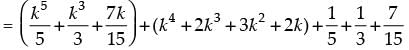
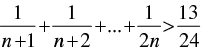 , for all natural numbers n > 1.
, for all natural numbers n > 1.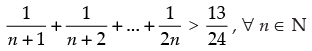
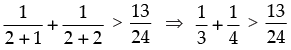
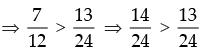 which is true for P(2).
which is true for P(2).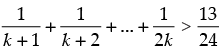 .Let it be true for P(k).
.Let it be true for P(k).