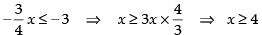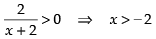Solve for x, the inequalities
Q.1. 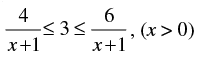
Ans.
Given that 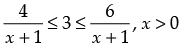
⇒ 4 ≤ 3(x + 1) ≤ 6 ⇒ 4 ≤ 3x + 3 ≤ 6
⇒ 4 – 3 ≤ 3x ≤ 6 – 3 ⇒ 1 ≤ 3x ≤ 3
⇒ 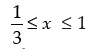
Hence, the solution is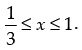
Q.2. 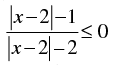
Ans.
Given that 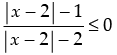
Put 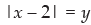
∴ 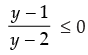
⇒ y – 1 > 0, y – 2 < 0 ⇒ y > 1, y < 2
⇒ 1 < y < 2 ⇒ 1 <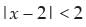
⇒ 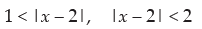
⇒ x – 2 < – 1 or x – 2 > 1 and – 2 < x – 2 < 2
⇒ x < 1 or x > 3 and – 2 + 2 < x < 2 + 2
⇒ x < 1 or x > 3 and 0 < x < 4
Hence, the required solution is (0, 1) ∪ (3, 4)
Q.3. 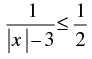
Ans.
Given that 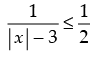
⇒ 
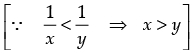

⇒ 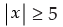
⇒ x ≤ - 5 or x ≥ 5
So, x ∈ ( - ∞,- 5] ∪ [5, ∞ ) ……(i)
Here 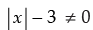
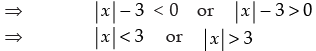
⇒ - 3 < x < 3 or x < - 3 or x > 3 ……(ii)
From in eq. (i) and (ii) we get
x ∈ (-∞ , - 5] ∪ (- 3, 3) ∪ [5, ∞)
Q.4. 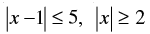
Ans.
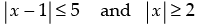
⇒ - 5 ≤ x – 1 ≤ 5 and x ≤ - 2 or x ≥ 2
⇒ - 5 + 1 ≤ x ≤ 5 + 1
⇒ - 4 ≤ x ≤ 6 and x ≤ - 2 or x ≥ 2
Hence x < [- 4, - 2] ∪ [2, 6]
Q.5. 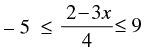
Ans.
Given that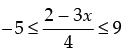
⇒ - 20 ≤ 2 – 3x ≤ 36 ⇒ - 20 – 2 ≤ - 3x ≤ 36 – 2
⇒ - 22 ≤ - 3x ≤ 34 ⇒ 22 ≥ 3x ≥ - 34
⇒ 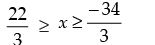
Hence 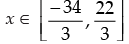
Q.6. 4x + 3 ≥ 2x + 17, 3x – 5 < – 2.
Ans.
Given that 4x + 3 ≥ 2x + 17 ...(i)
3x – 5 < – 2 ...(ii)
from eq. (i) we get
4x + 3 ≥ 2x + 17 ⇒ 4x – 2x ≥ 17 – 3
⇒ 2x ≥ 14 ⇒ x ≥ 7
From in eq. (ii) we get, 3x – 5 < - 2
⇒ 3x < 5 – 2 ⇒ 3x < 3
⇒ x < 1
We set that the solution x ≥ 7 and x < 1 is not possible. Hence there will be no solution of x.
Q.7. A company manufactures cassettes. Its cost and revenue functions are C(x) = 26,000 + 30x and R(x) = 43x, respectively, where x is the number of cassettes produced and sold in a week. How many cassettes must be sold by the company to realise some profit?
Ans.
Given that: Cost function, C(x) = 26,000 + 30x
and revenue function R(x) = 43x
Now for profit P(x), R(x) > C(x)
⇒ 43x > 26000 + 30x ⇒ 26000 + 30x < 43x
⇒ 30x – 43x < – 26000 ⇒ – 13x < – 26000
⇒ 13x > 26000 ⇒ x > 2000
Hence, number of cassettes to be manufactured for some profit must be more than 2000.
Q.8. The water acidity in a pool is considered normal when the average pH reading of three daily measurements is between 8.2 and 8.5. If the first two pH readings are 8.48 and 8.35, find the range of pH value for the third reading that will result in the acidity level being normal.
Ans.
Let the third pH value be x.
Given that first pH value = 8·48
and second pH value = 8·35
∴ Average value of pH = 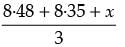
But average value of pH lies between 8·2 and 8·5
∴ 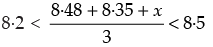
⇒ 24·6 < 16·83 + x < 25·5
⇒ 24·6 – 16·83 < x < 25·5 – 16·83
⇒ 7·77 < x < 8·67
Hence, the third pH value lies between 7·77 and 8·67.
Q.9. A solution of 9% acid is to be diluted by adding 3% acid solution to it. The resulting mixture is to be more than 5% but less than 7% acid. If there is 460 litres of the 9% solution, how many litres of 3% solution will have to be added?
Ans.
Let x litres of 3% solution be added to 460 litres of 9%.
∴ Total amount of mixture = (460 + x) litres
Given that the acid contents in the resulting mixture is more than 5% but less than 7% acid.
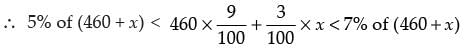

⇒ 5(460 + x) < 4140 + 3x < 3220 + 7x
⇒ 2300 + 5x < 4140 + 3x < 3220 + 7x
⇒ 2300 + 5x < 4140 + 3x and 4140 + 3x < 3220 + 7x
⇒ 5x – 3x < 4140 – 2300 and 3x – 7x < 3220 – 4140
⇒ 2x < 1840 and – 4x < – 920
⇒ 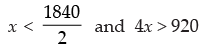
⇒ 
and x > 230
Hence the required amount of acid solution is more than 230 litres and less than 920 litres.
Q.10. A solution is to be kept between 40°C and 45°C. What is the range of temperature in degree fahrenheit, if the conversion formula is F = 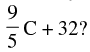
Ans.
Given that the range of temperature of the solution is 40°C and 45°C
Formula of conversion is F =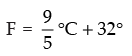
⇒ 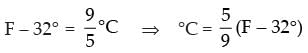
40° < °C < 45°
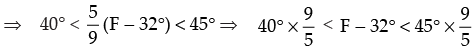
⇒ 72° < F – 32° < 81° ⇒ 72° + 32° < F < 81° + 32°
⇒ 104° < F < 113°
Hence, the require range is 104°F to 113°F.
Q.11. The longest side of a triangle is twice the shortest side and the third side is 2cm longer than the shortest side. If the perimeter of the triangle is more than 166 cm then find the minimum length of the shortest side.
Ans.
Let the length of the shortest side be x cm
∴ Length of the longest side = 2x cm
and the length of the third side = (x + 2) cm
Perimeter of the triangle = x cm + 2x cm + (x + 2) cm = (4x + 2) cm
As per the condition of the question, Perimeter > 166 cm
⇒ 4x + 2 > 166 ⇒ 4x > 166 - 2
⇒ 4x > 164 ⇒ x > 41 cm
Hence, the minimum length of the shortest side of the triangle is 41 cm.
Q.12. In drilling world’s deepest hole it was found that the temperature T in degree celcius, x km below the earth’s surface was given by T = 30 + 25 (x – 3), 3 ≤ x ≤ 15. At what depth will the temperature be between 155°C and 205°C?
Ans.
Given that, Temperature, T = 30° + 25° (x – 3), 3 ≤ x ≤ 15
Range of the temperature is 155°C to 205°C
∴ 155° < T < 205°
⇒ 155° < 30° + 25°(x – 3) < 205°
⇒ 125° < 25°(x – 3) < 175°
⇒ 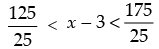
⇒ 5 < x – 3 < 7
⇒ 8 < x < 10
Hence the required temperature at the depth from 8 km to 10 km lies between 155°C and 205°C.
Q.13. Solve the following system of inequalities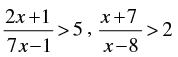
Ans.
Let us first take the inequation
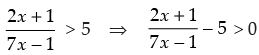
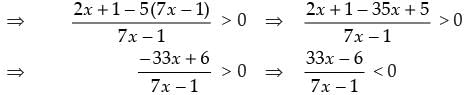
So 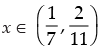 ..(i)
..(i)
Now from second inequality, we have
⇒ 
So x ∈ (8, 23) ...(ii)
Now nothing is common to the two values of x i.e. null set.
Hence, the given inequations has no solution.
Q.14. Find the linear inequalities for which the shaded region in the given figure is the solution set.
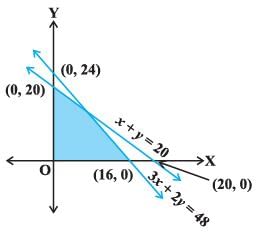
Ans.
Let us first consider the linear equation 3x + 2y = 48. We observe that the shaded region and the origin both on the same side of the graph of the line and (0, 0) satisfy the constraint 3x + 2y ≤ 48.
Similarly, we observe that the shaded region and the origin both on the same side of the graph of the line and (0, 0) satisfy the constraint x + y ≤ 20.
We also notice that the shaded region is in the first quadrant where x > and y > 0 Hence, the required linear inequalities are 3x + 2y ≤ 48, x + y ≤ 20, x ≥ 0, y ≥ 0
Q.15. Find the linear inequalities for which the shaded region in the given figure is the solution set.
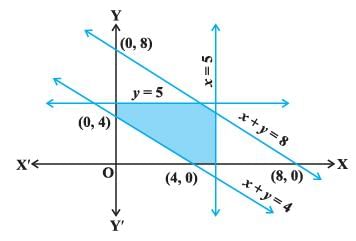
Ans.
Let us first consider the line x + y = 4 We observe that the shaded region and the origin (0, 0) are on the opposite side and (0, 0) satisfies the constraint x + y ≤ 4. So, x + y ≥ 4 is the linear inequality.
Now, take the linear equation x + y = 8.
In this case, the shaded region and the origin (0, 0) lie on the same side and (0, 0) also satisfies the constraint x + y ≤ 8.
So, x + y ≤ 8 is another linear inequality Consider, x = 5. It is clear that the shaded area lies towards the origin. So x ≤ 5 is the constraints and similarly y ≤ 5 is also the constraints. We also observe that the shaded region lies in first quadrant, so x ≥ 0, y ≥ 0.
Hence, the required system of inequalities is x + y ≥ 4, x + y ≤ 8, x ≤ 5, y ≤ 5, x ≥ 0, y ≥ 0.
Q.16. Show that the following system of linear inequalities has no solution x + 2y ≤ 3, 3x + 4y ≥ 12, x ≥ 0, y ≥ 1
Ans.
Given that: x + 2y ≤ 3, 3x + 4y ≥ 12, x ≥ 0, y ≥ 1
Let x + 2y = 3 ⇒ x = 3 - 2y
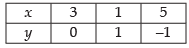
Now putting (0, 0) in x + 2y ≤ 3
0 + 0 ≤ 3
0 ≤ 3 True
Therefore, the shading will be towards (0, 0) Consider the in equation 3x + 4y ≥ 12
Let 3x + 4y = 12
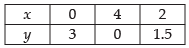
Putting (0, 0) in 3x + 4y ≥ 12
0 + 0 ≥ 12
0 ≥ 12 False
Therefore, shading will be on the opposite side of the graph of line.
x ≥ 0 ⇒ positive side of y-axis will be shaded.
and y ≥ 1 ⇒ upper side of y = 1 will be shaded.
Let us now draw the graph. It is clear from the graph that there is no common shaded region. Hence, the solution is null set.
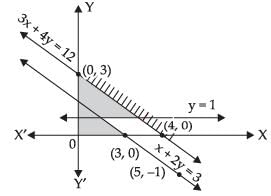
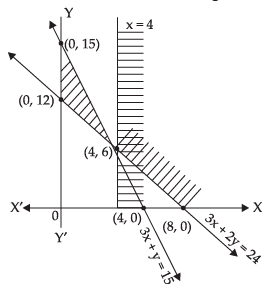
Q.17. Solve the following system of linear inequalities:
3x + 2y ≥ 24, 3x + y ≤ 15, x ≥ 4
Ans.
Given that 3x + 2y ≥ 24 ...(i)
Let 3x + 2y = 24;
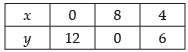
We observe that the graph of (i) inequality meets x-axis at (8, 0) and y-axis at (0, 12).
The origin (0, 0) does not satisfy the inequation (i) So, the shading will be on opposite side of the origin.
From inequation (ii) 3x + y ≤ 15
Let 3x + y = 15
Put a point (0, 0) in inequation (ii) we get
0 + 0 ≤ 15
0 ≤ 15 True
So, the shading will be on the same side where the origin lies. Now drawing x ≥ 4, we observe a straight line parallel to y-axis passing through a point (4, 0) which does not satisfy the equation. So, the shading will be on right side of the line.
Now it is clear from the graph that there is no region is common to all inequalities.
Hence, the given system of inequalities has no solution.
Q.18. Show that the solution set of the following system of linear inequalities is an unbounded region
2x + y ≥ 8, x + 2y ≥ 10, x ≥ 0, y ≥ 0
Ans.
Let us consider the inequality 2x + y ≥ 8 as an equation

The line 2x + y = 8 intersects x-axis at (4, 0) and y-axis at (0, 8 ) The origin (0, 0) does not satisfy the inequation 2x + y ≥ 8 Therefore shading will be done opposite side of the origin.
Let us consider x + 2y ≥ 10 as an equation x + 2y = 10.
The x + 2y = 10 meets the axes at (10, 0) and (0, 5) The origin (0, 0) does not satisfy the in equation x + 2y ≥ 10 Therefore, shading will be done on the opposite side of the origin

It is clear from the graph that the common shaded region is unbounded.
Objective Type Question
Q.19. If x < 5, then
(a) – x < – 5
(b) – x ≤ – 5
(c) – x > – 5
(d) – x ≥ – 5
Ans. (c)
Solution.
If x < 5 then – x > – 5
Here, the correct option is (c).
Q.20. Given that x, y and b are real numbers and x < y, b < 0, then
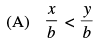
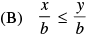
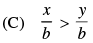
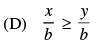
Ans. (c)
Solution.
Given that x < y, b < 0
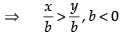
Hence, the correct option is (c).
Q.21. If – 3x + 17 < – 13, then
(A) x ∈ (10, ∞)
(B) x ∈ [10, ∞)
(C) x ∈ (– ∞, 10]
(D) x ∈ [– 10, 10)
Ans. (a)
Solution.
Given that – 3x + 17 < – 13
⇒ – 3x < – 17 – 13 ⇒ – 3x < – 30
⇒ 3x > 30 ⇒ x > 10
⇒ x ∈ (10, ∞)
Hence, the correct option is (a).
Q.22. If x is a real number and | x | < 3, then
(a) x ≥ 3
(b) – 3 < x < 3
(c) x ≤ – 3
(d) – 3 ≤ x ≤ 3
Ans. (b)
Solution.
Given that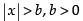
⇒ – 3 < x < 3 
Hence, the correct option is (b).
Q.23. x and b are real numbers. If b > 0 and | x | > b, then
(a) x ∈ (– b, ∞)
(b) x ∈ [– ∞, b)
(c) x ∈ (– b, b)
(d) x ∈ (– ∞, – b) ∪ (b, ∞)
Ans. (d)
Solution.
Given that |x| > b, b > 0
⇒ x < - b or x > b
⇒ x ∈ (-∞ , - b) ∪ (b, ∞ )
Hence the correct option is (d)
Q.24. If x − 1 > 5, then
(a) x ∈ (– 4, 6)
(b) x ∈ [– 4, 6]
(c) x ∈ [– ∞, – 4) ∪ (6, ∞)
(d) x ∈ [– ∞, – 4) ∪ [6, ∞)
Ans. (c)
Solution.
Given that |x – 1| > 5
⇒ (x – 1) < - 5 or (x – 1) > 5
⇒ x < - 5 + 1 or x > 5 + 1
⇒ x < - 4 or x >6
⇒ x ∈ (-∞ , - 4) ∪ (6, ∞)
Hence, the correct option is (c).
Q.25. If x + 2 ≤ 9, then
(A) x ∈ (– 7, 11)
(B) x ∈ [– 11, 7]
(C) x ∈ (– ∞, – 7) ∪ (11, ∞)
(D) x ∈ (– ∞, – 7) ∪ [11, ∞)
Ans. (b)
Solution.
Given that |x + 2| ≤ 9
⇒ - 9 ≤ x + 2 ≤ 9
⇒ - 9 – 2 ≤ x ≤ 9 – 2 [|x| ≤ a ⇒ - a ≤ x ≤ a]
⇒ - 11 ≤ x ≤ 7
⇒ x ∈ [- 11, 7]
Hence, the correct option is (b),
Q.26. The inequality representing the following graph is:
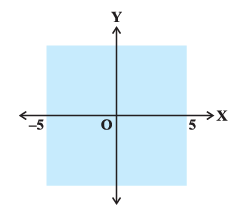
(a) | x | < 5
(b) | x | ≤ 5
(c) | x | > 5
(d) | x | ≥ 5
Ans. (a)
Solution.
The given graph represents
x > - 5 and x < 5
Combining the two inequalities
|x| < 5
The correct option is (a).
Solution of a linear inequality in variable x is represented on number line
Choose the correct answer from the given four options in each of the exercises (M.C.Q.).
Q.27. (a) x ∈ (– ∞, 5)
(b) x ∈ (– ∞, 5]
(c) x ∈ [5, ∞,)
(d) x ∈ (5, ∞)
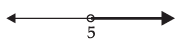
Ans. (d)
Solution.
The gives graph represents all values of x greater than 5 including 5 on the real number line
So, x ∈ (5, ∞)
Hence, the correct option is (d).
Q.28. (a) x ∈ ( 9/2, ∞)
(b) x ∈ [ 9/2, ∞)
(c) x ∈ [– ∞, 9/2)
(d) x ∈ (– ∞, 9/2]
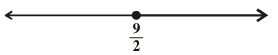
Ans. (b)
Solution.
The given graph has all real values of x greater than and equal to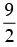 .
.
Hence, the correct option is (b).
Q.29. (a) x ∈ (– ∞, 7/2)
(b) x ∈ (– ∞, 7/2]
(c) x ∈ [ 7/2, – ∞)
(d) x ∈ ( 7/2, ∞)
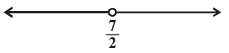
Ans. (a)
Solution.
The given graph represents all the values of x less than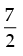 on real number line.
on real number line.
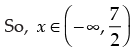
Hence, the correct option is (a).
Q.30. (a) x ∈ (– ∞, – 2)
(b) x ∈ (– ∞, – 2]
(c) x ∈ (– 2, ∞]
(d) x ∈ [– 2, ∞)
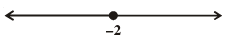
Ans. (b)
Solution.
The given graph represents all real values of x less than and equal to – 2
So, x ∈ (-∞ , - 2]
Hence, the correct option is (b).
State which of the following statements is True or False
Q.31. (i) If x < y and b < 0, then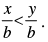
(ii) If xy > 0, then x > 0 and y < 0
(iii) If xy > 0, then x < 0 and y < 0
(iv) If xy < 0, then x < 0 and y < 0
(v) If x < –5 and x < –2, then x ∈ (– ∞, – 5)
(vi) If x < –5 and x > 2, then x ∈ (– 5, 2)
(vii) If x > –2 and x < 9, then x ∈ (– 2, 9)
(viii) If | x | > 5, then x ∈ (– ∞, – 5) ∪ [5, ∞)
(ix) If | x | ≤ 4, then x ∈ [– 4, 4]
(x) Graph of x < 3 is
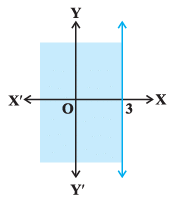
(xi) Graph of x ≥ 0 is
(xii) Graph of y ≤ 0 is
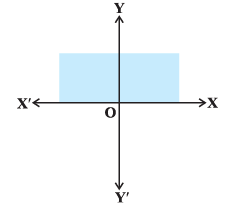
(xiii) Solution set of x ≥ 0 and y ≤ 0 is
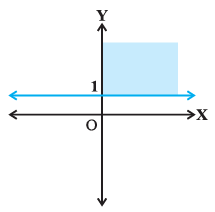
(xiv) Solution set of x ≥ 0 and y ≤ 1 is
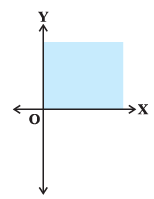
(xv) Solution set of x + y ≥ 0 is
Ans.
(i) If x < y and b < 0
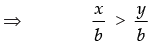
Hence, statement (i) is False.
(ii) If x, y > 0 then x > 0, y > 0 or x < 0, y < 0
Statement (ii) is False.
(iii) If xy > 0 then x < 0 and y < 0
Hence, the statement (iii) is True.
(iv) If xy < 0 ⇒x < 0 and y > 0 or x > 0, y < 0
Hence, the statement (iv) is False.
(v) If x < - 5 and x < - 2 ⇒ x ∈ (- ∞, - 5)
Hence, the statement (v) is True.
(vi) If x < - 5 and x > 2, then x have no value.
Hence, the statement (vi) is False.
(vii) If x > - 2 and x < 9 then x ∈ (- 2, 9)
Hence, the statement (vii) is True.
(viii) If |x| > 5 then x < - 5 or x > 5
⇒ x ∈ (- ∞, - 5) ∪ (5, ∞)
Hence, the statement (viii) is False.
(ix) If |x| ≤ 4 then – 4 ≤ x ≤ 4
⇒ x ∈ [- 4, 4]
Hence, the statement (ix) is True.
(x) The given graph represents x ≤ 3
Hence, the statement (x) is False.
(xi) The given graph represents x ≥ 0
Hence, the statement (xi) is True.
(xii) The given graph represents y ≥ 0
Hence, the statement (xii) is False.
(xiii) Solution set of x ≥ 0 and y ≤ 0 is
Hence, the statement (xiii) is False.
(xiv) Solution set of x ≥ 0 and y ≤ 1 is
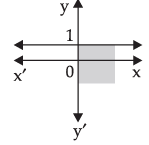
Hence, the statement (xiv) is False.
(xv) The given graph represents x + y ≥ 0
Hence, the statement (xv) is True.
Q.32. Fill in the blanks of the following:
(i) If – 4x ≥ 12, then x ... – 3.
(ii) If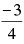 x ≤ – 3, then x ... 4.
x ≤ – 3, then x ... 4.
(iii) If 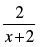 > 0, then x ... –2.
> 0, then x ... –2.
(iv) If x > – 5, then 4x ... –20.
(v) If x > y and z < 0, then – xz ... – yz.
(vi) If p > 0 and q < 0, then p – q ... p.
(vii) If x + 2 > 5, then x ... – 7 or x ... 3.
(viii) If – 2x + 1 ≥ 9, then x ... – 4.
Ans.
(i) – 4 x ≥ 12 ⇒ x ≤ - 3
Hence, the filler is (≤)
(ii) If 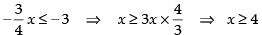
Hence, the filler is (≥)
(iii) If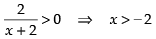
Hence, the filler is (>)
(iv) If x > –5 ⇒ 4x > - 20
Hence, the filler is (>)
(v) If x > y and z < 0, then
xz < yz ⇒ - xz > - yz
Hence, the filler is (>)
(vi) If p > 0 and q < 0 then p - q > p
Hence, the filler is (>)
(vii) If |x + 2|> 5 then
x + 2 < - 5 or x + 2 > 5
⇒ x < - 5 – 2 or x > 5 – 2
⇒ x < - 7 or x > 3
So x ∈ (-∞, - 7) ∪ (3, ∞)
Hence, the filler is (<) or (>)
(viii) If – 2x + 1 ≥ 9 then
-2x ≥ 9 – 1 ⇒ - 2x ≥ 8 ⇒ 2x ≤ - 8 ⇒ x ≤ - 4
Hence, the filler is (≤).
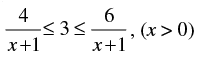
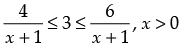
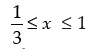
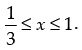
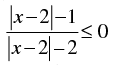
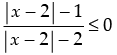
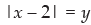
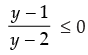
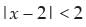
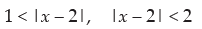
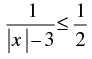
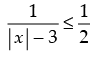

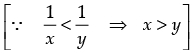

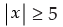
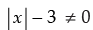
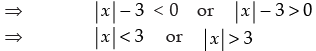
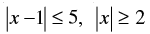
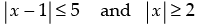
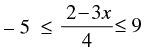
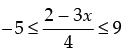
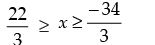
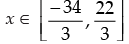
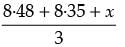
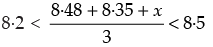
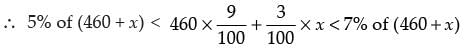

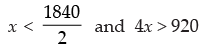

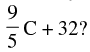
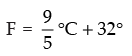
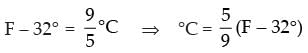
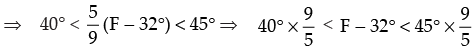
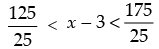
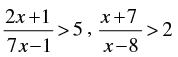
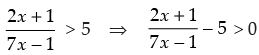
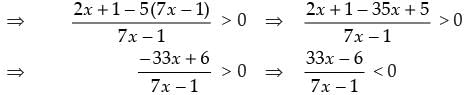
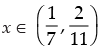 ..(i)
..(i)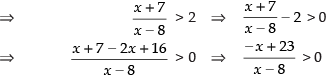












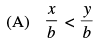
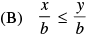
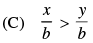
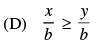
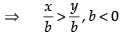
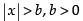
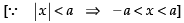

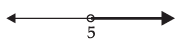
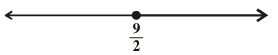
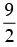 .
.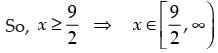
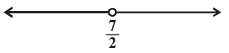
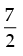 on real number line.
on real number line.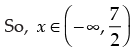
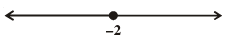
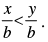





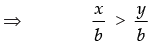


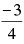 x ≤ – 3, then x ... 4.
x ≤ – 3, then x ... 4.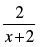 > 0, then x ... –2.
> 0, then x ... –2.