NCERT Exemplar: Limits and Derivatives | Mathematics (Maths) Class 11 - Commerce PDF Download
Evaluate :
Q.1.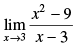 
Ans.
Given that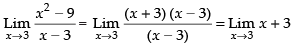 
Taking limit, we have
3 + 3 = 6
Hence, the answer is 6.
Q.2.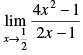 
Ans.
Given that: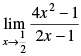
=
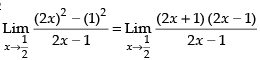
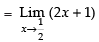
Taking limit, we have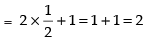
Hence, the answer is 2.
Q.3.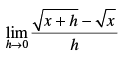 
Ans.
Given that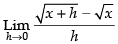
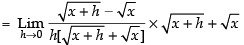
[Rationalizing the denominator]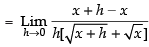
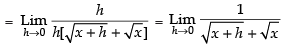
Taking the limits, we have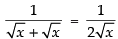
Hence, the answer is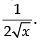
Q.4.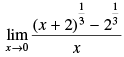 
Ans.
Given that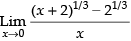 
Put x + 2 = y ⇒ x = y – 2
Hence the answer is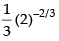
Q.5.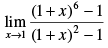 
Ans.
Given that: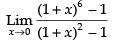 
Dividing the numerator and denominator by x, we get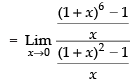
Putting 1 + x = y ⇒ x = y – 1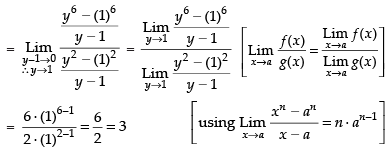
Hence, the required answer is 3.
Q.6.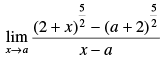 
Ans.
Given that: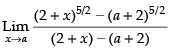
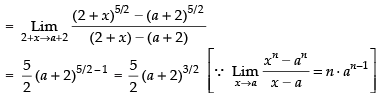
Hence, the required answer is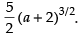
Q.7.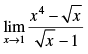 
Ans.
Given that: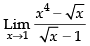 
=
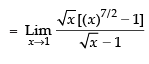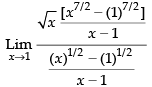
[Dividing the numerator and denominator of x –1]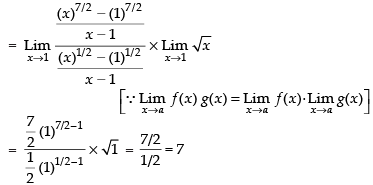
Hence the required answer is 7.
Q.8.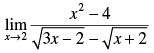 
Ans.
Given that:
Rationalizing the denominator, we get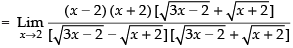
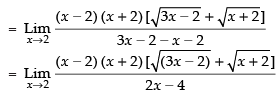
Taking limits, we have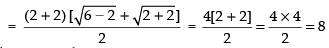
Hence, the required answer is 8.
Q.9.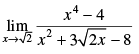 
Ans.
Given that :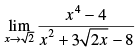 
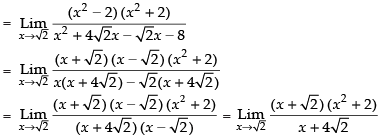
Taking limits we have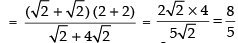
Hence, the required answer is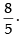
Q.10.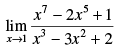 
Ans.
Given that: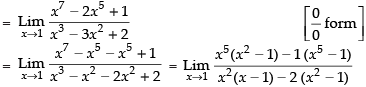
Dividing the numerator and denominator by (x – 1) we get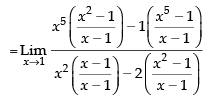
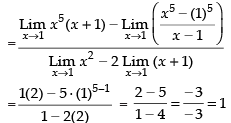
Hence, the required answer is 1.
Q.11.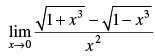 
Ans.
Given that: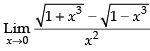
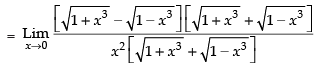
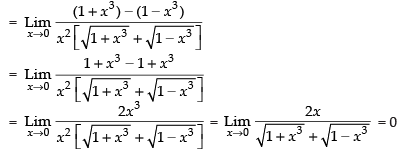
Hence, the required answer is 0.
Q.12.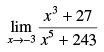 
Ans.
Given that: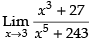 
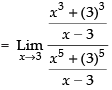[Dividing the Nr and Den. by x – 3]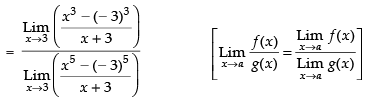
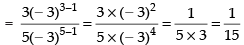
Hence, the required answer is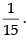
Q.13.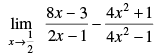 
Ans.
Given that :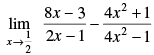
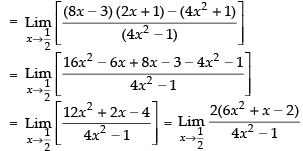
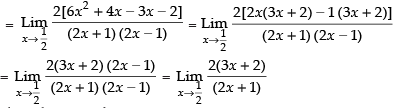
Taking limit, we have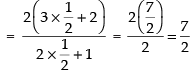
Hence, the required answer is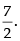
Q.14. Find ‘n’, if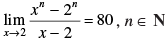
Ans.
Given that: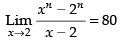
= n × (2)n-1 = 80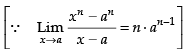
= n x 2n-1 = 5 x (2)5-1
∴ n = 5
Hence, the required answer is n = 5.
Q.15.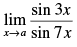 
Ans.
Given that: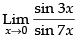
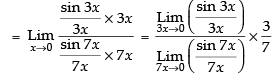
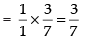
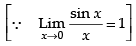
Hence, the required answer is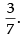
Q.16.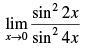 
Ans.
Given that: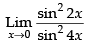
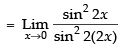
[sin 2x = 2 sin x cos x]
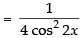
Taking limit we have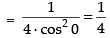
Hence, the required answer is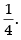
Q.17.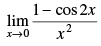 
Ans.
Given that: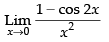
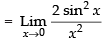[cos 2x = 1 – 2 sin2 x]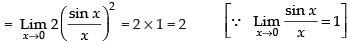
Hence, the required answer is 2.
Q.18.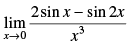 
Ans.
Given that: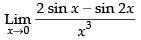
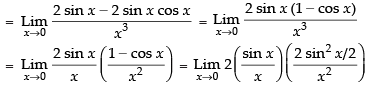
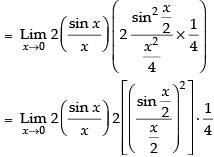
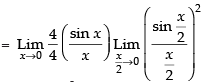
= 1 × 1 × (1)2 = 1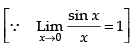
Hence, the required answer is 1.
Q.19.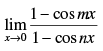 
Ans.
Given that: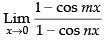
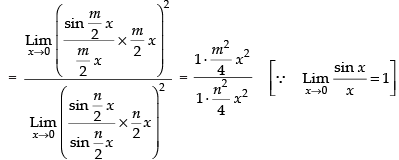
Hence, the required answer is
Q.20. 
Ans.
Given that: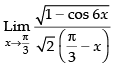
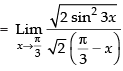[∴ 1 - cosθ = 2 sin2 θ/2]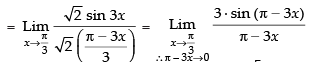
= 3
Hence, the required answer is 3.
Q.21.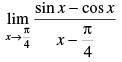 
Ans.
Given that: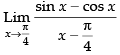
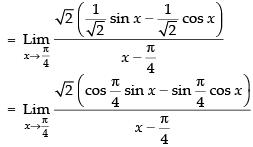
√2 ×1 = √2
Hence, the required answer is √2 .
Q.22.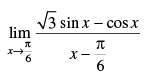 
Ans.
Given that:
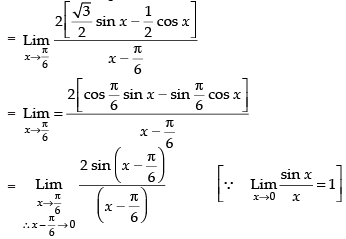
= 2 × 1 = 2
Hence, the required answer is 2.
Q.23.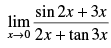 
Ans.
Given that: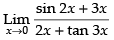
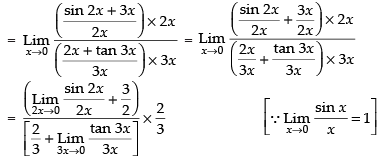
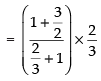
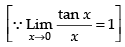
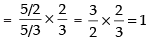
Hence, the required answer is 1.
Q.24.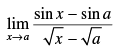 
Ans.
Given that: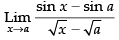
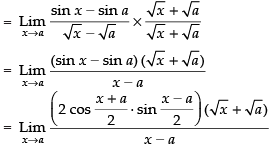
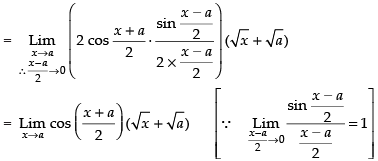
Taking limit we have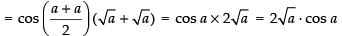
Hence, the required answer is 2 √a cos a.
Q.25.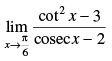 
Ans.
Given that: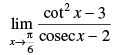
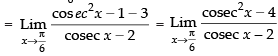
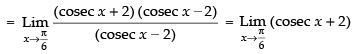
Taking limit we have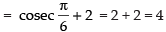
Hence, the required answer is 4.
Q.26.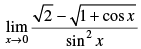 
Ans.
Given that: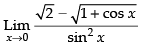
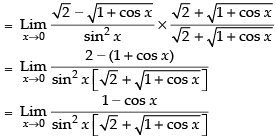
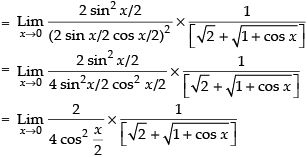
Taking limit, we get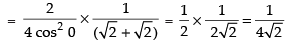
Hence, the required answer is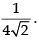
Q.27.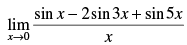 
Ans.
Given that: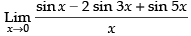
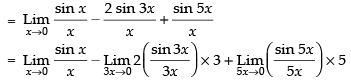
= 1 – 6 + 5 = 0
Hence, the required answer is 0.
Q.28. If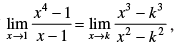 
then find the value of k.
Ans.
Given that: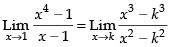
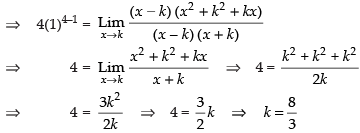
Hence, the required value of k is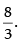
Differentiate each of the functions from Q. 29 to Q. 42
Q.29.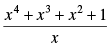 
Ans.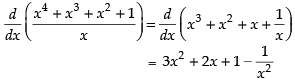
Hence, the required answer is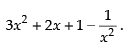
Q.30.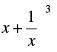 
Ans.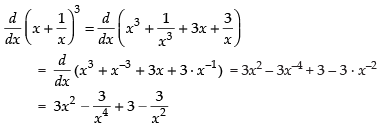
Hence, the required answer is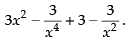
Q.31. (3x + 5) (1 + tanx)
Ans.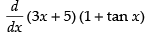
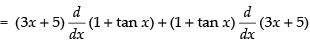
= (3x + 5) (sec2x) + (1 + tan x) (3)
= 3x sec2 x + 5 sec2 x + 3 + 3 tan x [using product rule]
Hence, the required answer is 3x sec2 x + 5 sec2 x + 3 tan x + 3
Q.32. (sec x – 1) (sec x + 1)
Ans.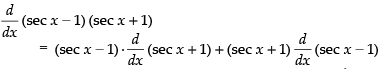
[using product rule]
= (sec x – 1) (sec x tan x) + (sec x + 1) (sec x tan x)
= sec x tan x (sec x – 1 + sec x + 1)
= sec x tan x × 2 sec x
= 2 sec2 x × tan x
Hence, the required answer is 2 tan x sec2 x.
Q.33.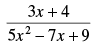 
Ans.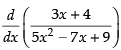
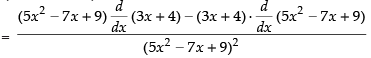
[Using quotient rule]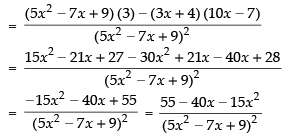
Hence, the required answer is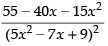 
Q.34.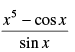 
Ans.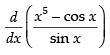
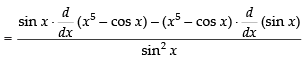
[Using quotient rule]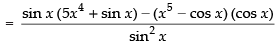
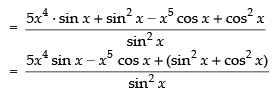
Hence, the required answer is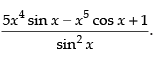
Q.35. 
Ans.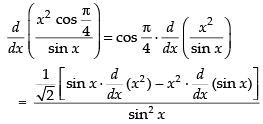
[Using quotient rule]
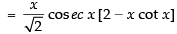
Hence, the required answer is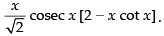
Q.36. (ax2 + cotx) (p + q cosx)
Ans.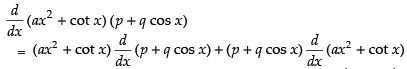
[Using Product Rule]
= (ax2 + cot x) (- q sin x) + (p + q cos x) (2ax - cosec2 x)
Hence, the required answer is
= (ax2 + cot x) (- q sin x) + (p + q cos x) (2ax - cosec2 x)
Q.37.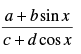 
Ans.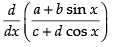
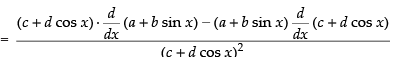
[Using quotient rule]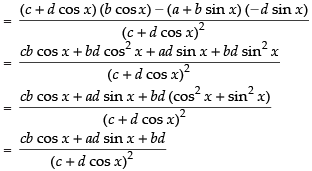
Q.38. (sin x + cosx)2
Ans.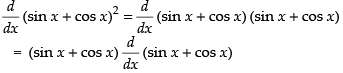
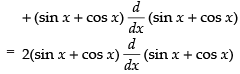
= 2(sin x + cos x) (cos x - sin x) = 2(cos2 x - sin2 x) = 2 cos 2x
Hence, the required answer is 2 cos 2x.
Q.39. (2x – 7)2 (3x + 5)3
Ans.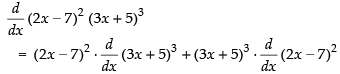
Using product Rule]
= (2x – 7)2 × 3(3x + 5)2 × 3 + (3x + 5)3 × 2(2x - 7) × 2
= 9(2x - 7)2 (3x + 5)2 + 4(3x + 5)3 (2x - 7)
= (2x - 7) (3x + 5)2 [9(2x - 7) + 4(3x + 5)]
= (2x - 7) (3x + 5)2 (18x - 63 + 12x + 20)
= (2x - 7) (3x + 5)2 (30x - 43)
Hence, the required answer is (2x - 7) (30x - 43) (3x + 5)2
Q.40. x2 sinx + cos2x
Ans.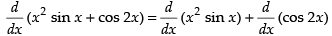
= (x2 cos x + sin x × 2 x) + (- 2 sin 2 x)
= x2 cos x + 2x sin x - 2 sin 2x
Hence, the required answer is x2 cos x + 2x sin x - 2 sin 2x.
Q.41. sin3x cos3x
Ans.
[Using Product Rule]
= sin3 x × 3 cos2 x (– sin x) + cos3 x × 3 sin2 x × cos x
= - 3 sin4 x cos2 x + 3 cos4 x sin2 x
= 3 sin2 x cos2 x (- sin2 x + cos2 x)
= 3 sin2 x cos2 x × cos 2x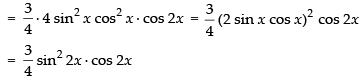
Hence, the required answer is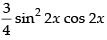
Q.42.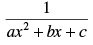 
Ans.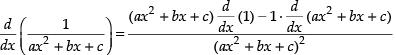
[Using quotient rule]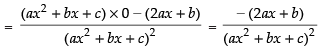
Hence, the required answer is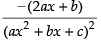
LONG ANSWER TYPE QUESTIONS
Differentiate each of the functions with respect to ‘x’ . Q.43 to Q.46 using first principle.
Q.43. cos (x2 + 1)
Ans.
Let f (x) = cos(x2 + 1) ...(i)
⇒ f (x + Δx) = cos [(x + Δx)2 + 1] ...(ii)
Subtracting eq. (i) from eq. (ii) we get
f (x + Δx) – f (x) = cos [(x + Δx)2 + 1] – cos(x2 + 1)
Dividing both side by Δx we get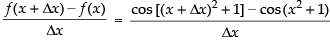
[By definitions of differentiations]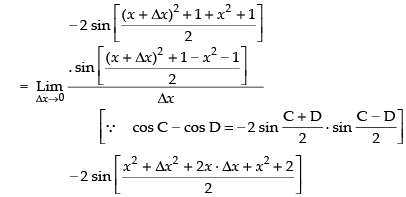
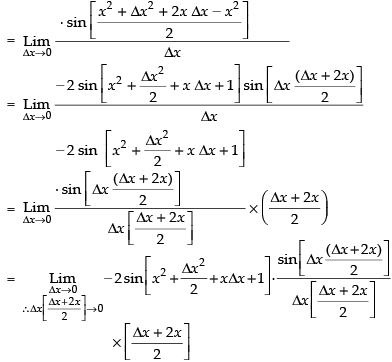
Taking limit, we have
= – 2 sin (x2 + 1) × 1 × (x) = - 2x sin (x2 + 1)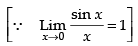
Hence, the required answer is – 2x sin (x2 + 1).
Q.44.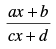 
Ans.
Let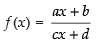
....(i)
⇒
....(ii)
Subtracting eq. (i) from eq. (ii) we get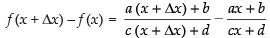
Dividing both sides by Δx and take the limit, we get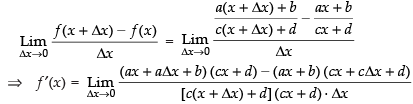
[Using definition of differentiation]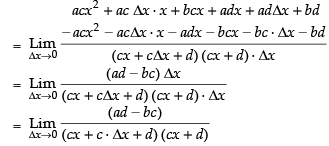
Taking limit, we have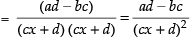
Hence, the required answer is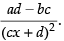
Q.45. x2/3
Ans.
Let f (x) = x2/3 ....(i)
f (x + Δx) = (x + Δx)2/3 ....(ii)
Subtracting eq. (i) from (ii) we get
f (x + Δx) – f (x) = (x + Δx)2/3 – x2/3
Dividing both sides by Δx and take the limit.
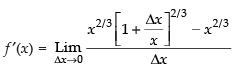
[By definition of differentiation]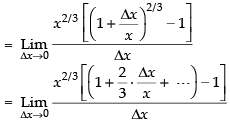
[Expanding by Binomial theorem and rejecting the higher powers of Δx as Δx → 0]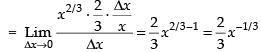
Hence, the required answer is
Q.46. x cosx
Ans.
Let y = x cos x ....(i)
y + Δy = (x + Δx) cos (x + Δx) ....(ii)
Subtracting eq. (i) from eq. (ii) we get
y + Δy – y = (x + Δx) cos (x + Δx) – x cos x
⇒ Δy = x cos (x + Δx) + Δx cos (x + Δx) – x cos x
Dividing both sides by Δx and take the limits,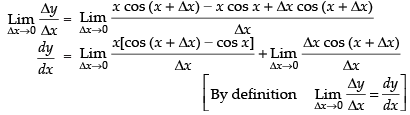
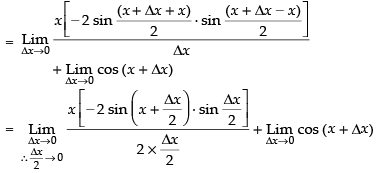
Taking the limits, we have
= x[– sin x] + cos x
= – x sin x + cos x
Hence, the required answer is – x sin x + cos x
Evaluate each of the following limits in Q.47 to Q.53.
Q.47.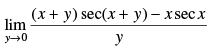 
Ans.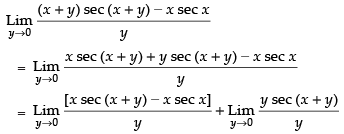
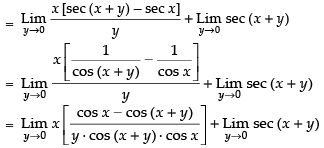
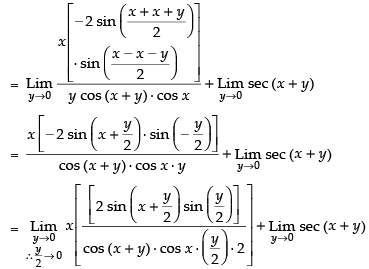
∴ Taking the limits we have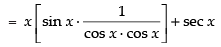
= x sec x tan x + sec x = sec x (x tan x + 1)
Hence, the required answer is sec x (x tan x + 1)
Q.48.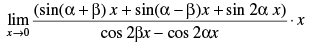 
Ans.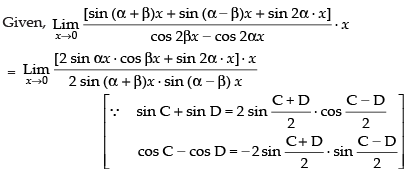
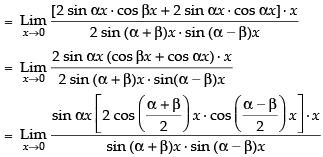
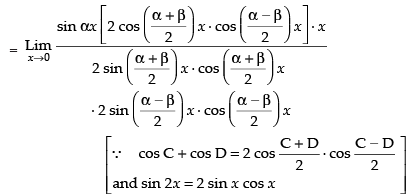
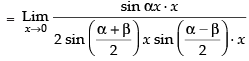
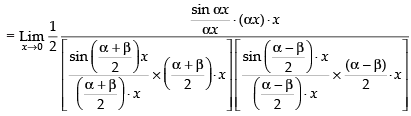
Hence, the required answer is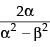
Q.49.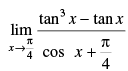 
Ans.
Given,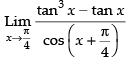 
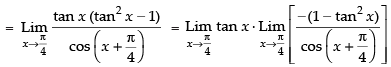
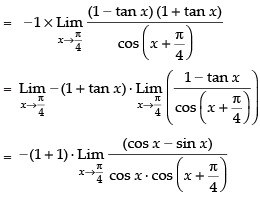
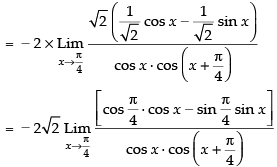
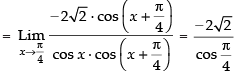(Taking limit)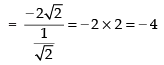
Hence, the required answer is – 4.
Q.50.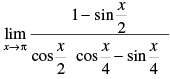 
Ans.
Given,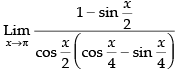
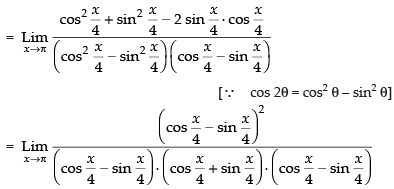
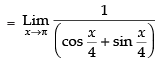
Taking limits we have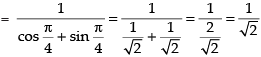
Hence, the required answer is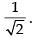
Q.51. Show that
does not exists
Ans.
Given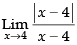 
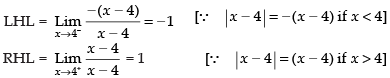
Since LHL ≠ RHL
Hence, the limit does not exist.
Q.52. Let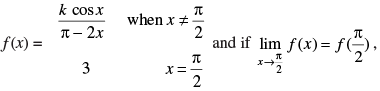
find the value of k.
Ans.
Given,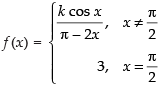
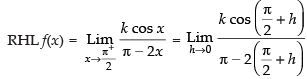
we are given that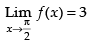
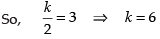
Hence, the required answer is 6.
Q.53. Let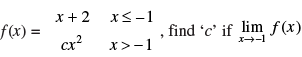
exists.
Ans.
Given,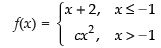
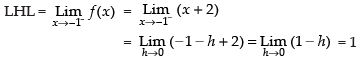
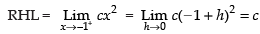
Since the limits exist.
∴ LHL = RHL
∴ c = 1
Hence, the required answer = 1
OBJECTIVE ANSWER TYPE QUESTIONS
Q.54.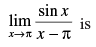 
(a) 1
(b) 2
(c) – 1
(d) – 2
Ans. (c)
Solution.
Given,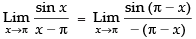
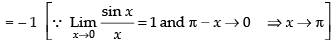
Hence, the correct option is (c).
Q.55.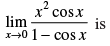 
(a) 2
(b) 3/2
(c) – 3/2
(d) 1
Ans. (a)
Solution.
Given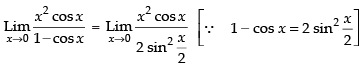
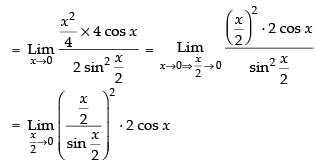
= 2 cos 0 = 2 x 1 = 2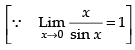
Hence, the correct option is (a).
Q.56. 
(a) n
(b) 1
(c) – n
(d) 0
Ans. (a)
Solution.
Given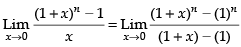 
Hence, the correct option is (a).
Q.57.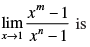 
(a) 1
(b) m/n
(c) – m/n
(d) m2/n2
Ans. (b)
Solution.
Given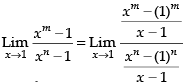 
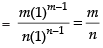
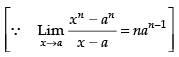
Hence, the correct option is (b).
Q.58.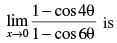 
(a) 4/9
(b) 1/2
(c) – 1/2
(d) –1
Ans. (a)
Solution.
Given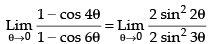 
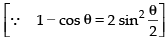
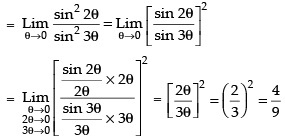
Hence, the correct option is (a).
Q.59.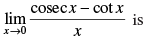 
(a) - 1/2
(b) 1
(c) 1/2
(d) – 1
Ans. (c)
Solution.
Given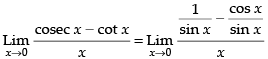
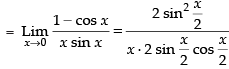
[∴ sin 2x = 2 sin x cos x]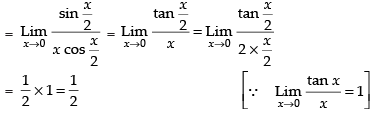
Hence, the correct option is (c).
Q.60.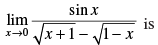 
(a) 2
(b) 0
(c) 1
(d) – 1
Ans. (c)
Solution.
Given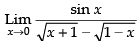 
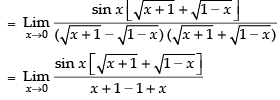
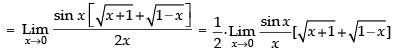
Taking limit, we get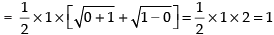
Hence, the correct option is (c).
Q.61.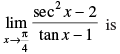 
(a) 3
(b) 1
(c) 0
(d) 2
Ans. (d)
Solution.
Given,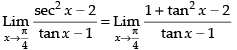
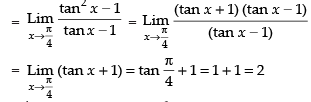
Hence, the correct option is (d).
Q.62.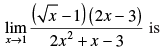 
(a) 1/10
(b) - 1/10
(c) 1
(d) None of these
Ans. (b)
Solution.
Given
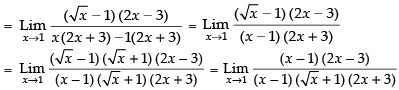
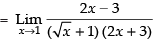
Taking limit we have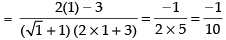
Hence, the correct option is (b).
Q.63.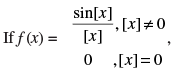 
where [.] denotes the greatest integer function then
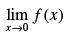is equal to
(a) 1
(b) 0
(c) – 1
(d) None of these
Ans. (d)
Solution.
Given,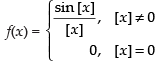
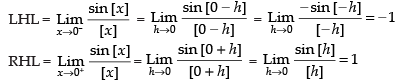
LHL ≠ RHL
So, the limit does not exist.
Hence, the correct option is (d).
Q.64.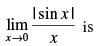 
(a) 1
(b) – 1
(c) Does not exist
(d) None of these.
Ans. (c)
Solution.
Given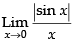 
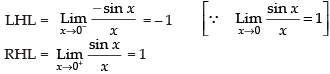
LHL ≠ RHL,
so the limit does not exist.
Hence, the correct option is (c).
Q.65. Let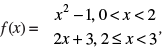 
the quadratic equation whose roots are 
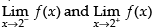is
(a) x2 – 6x + 9 = 0
(b) x2 – 7x + 8 = 0
(c) x2 – 14x + 49 = 0
(d) x2 – 10x + 21 = 0
Ans. (d)
Solution.
Given
∴
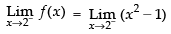
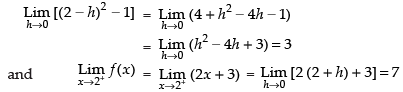
Therefore, the quadratic equation whose roots are 3 and 7 is
x2 – (3 + 7)x + 3 x 7 = 0 i.e., x2 - 10x + 21 = 0.
Hence, the correct option is (d).
Q.66.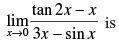 
(a) 2
(b) 1/2
(c) - 1/2
(d) 1
Ans. (b)
Solution.
Given
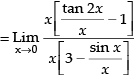
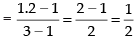
∴ 2x → 0
Hence, the correct option is (b).
Q.67. Let f (x) = x – [x]; ∈ R, then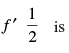
(a) 3/2
(b) 1
(c) 0
(d) – 1
Ans. (b)
Solution.
Given f (x) = x – [x]
we have to first check for differentiability of f (x) at x = 1/2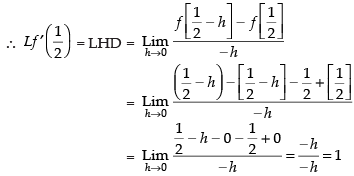
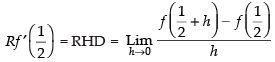
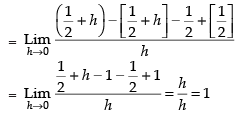
Since LHD = RHD
∴
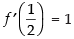
Hence, the correct option is (b).
Q.68. If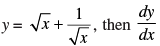
at x = 1 is
(a) 1
(b) 1/2
(c) 1/√2
(d) 0
Ans. (d)
Solution.
Given that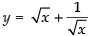
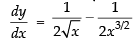
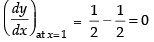
Hence, the correct option is (d).
Q.69. If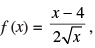 
then f ′(1) is
(a) 5/4
(b) 4/5
(c) 1
(d) 0
Ans. (a)
Solution.
Given that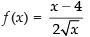 
∴
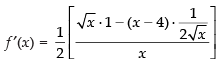
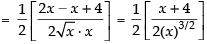
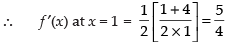
Hence, the correct option is (a).
Q.70. If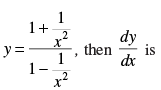
(a)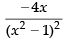 
(b)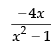
(c)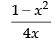
(d)
Ans. (a)
Solution.
Given
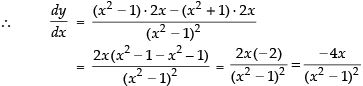
Hence, the correct option is (a).
Q.71. If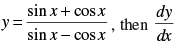
at x = 0 is
(a) – 2
(b) 0
(c) 1/2
(d) Does not exist
Ans. (a)
Solution.
Given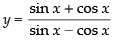 
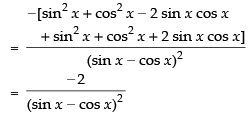
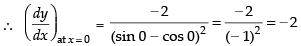
Hence, the correct option is (a).
Q.72. If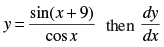
at x = 0 is
(a) cos 9
(b) sin 9
(c) 0
(d) 1
Ans. (a)
Solution.
Given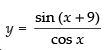
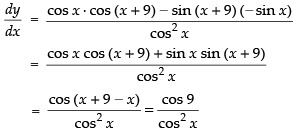
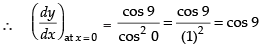
Hence, the correct option is (a).
Q.73. If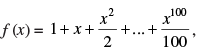
then f ′(1) is equal to
(a) 1/100
(b) 100
(c) does not exist
(d) 0
Ans. (b)
Solution.
Given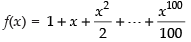
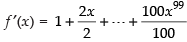
∴ f ’(1) = 1 + 1 + 1 + ..... + 1 (100 times) = 100
Hence, the correct option is (b).
Q.74. If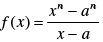
for some constant ‘a’, then f ′(a) is
(a) 1
(b) 0
(c) does not exist
(d) 1/2
Ans. (c)
Solution.
Given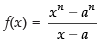
∴
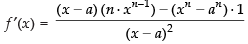
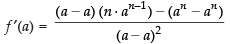
So
= does not exist
Hence, the correct option is (c).
Q.75. If f (x) = x100 + x99 + ... + x + 1, then f′(1) is equal to
(a) 5050
(b) 5049
(c) 5051
(d) 50051
Ans. (a)
Solution.
Given, f(x) = x100 + x99 + … + x + 1
∴ f′(x) = 100x99 + 99.x98 + ... + 1
So, f′ (1) = 100 + 99 + 98 + ... + 1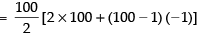
= 50[200 – 99] = 50 x 101 = 5050
Hence, the correct option is (a).
Q.76. If f (x) = 1 – x + x2 – x3 ... – x99 + x100, then f ′(1) is equal to
(a) 150
(b) – 50
(c) – 150
(d) 50
Ans. (d)
Solution.
Given that f (x) = 1 – x + x2 – x3 + … – x99 + x100
f′(x) = - 1 + 2x - 3x2 + ... - 99x98 + 100 x99
∴ f′(1) = - 1 + 2 - 3 + ... - 99 + 100
= (- 1 - 3 - 5 ... - 99) + (2 + 4 + 6 + ... + 100)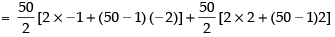
= 25[–2 – 98] + 25 [4 + 98]
= 25 x - 100 + 25 x 102
= 25[–100 + 102] = 25 x 2 = 50
Hence, the correct option is (d).
FILL IN THE BLANKS
Q.77. If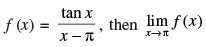
= _______
Ans.
Given
Hence, the value of the filler is 1.
Q.78.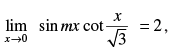 
then m = _______
Ans.
Given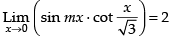
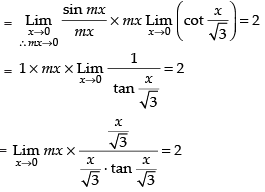
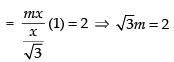
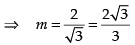
Hence, the value of the filler is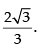
Q.79. if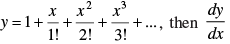
= _______
Ans.
Given that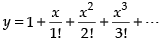
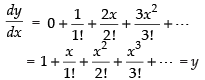
Hence the value of the filler is y.
Q.80.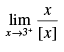 
= _______
Ans.
Given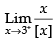
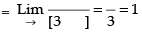
Hence, the value of the filler is 1.
|
75 videos|238 docs|91 tests
|
FAQs on NCERT Exemplar: Limits and Derivatives - Mathematics (Maths) Class 11 - Commerce
| 1. What is the concept of a limit in calculus? |  |
| 2. How do you calculate the limit of a function? | |
| 3. What are the properties of limits in calculus? | |
| 4. How are limits used to find derivatives? | |
| 5. What are the applications of limits and derivatives in real-life situations? | |
|
1.2K Views |
|
4.63/5 Rating |
|
Dec 22, 2024 Last updated |
|
Explore Courses for Commerce exam
|
|
Important questions
,Sample Paper
,NCERT Exemplar: Limits and Derivatives | Mathematics (Maths) Class 11 - Commerce
,Extra Questions
,Free
,shortcuts and tricks
,MCQs
,NCERT Exemplar: Limits and Derivatives | Mathematics (Maths) Class 11 - Commerce
,Objective type Questions
,study material
,ppt
,video lectures
,mock tests for examination
,practice quizzes
,past year papers
,NCERT Exemplar: Limits and Derivatives | Mathematics (Maths) Class 11 - Commerce
,Semester Notes
,Previous Year Questions with Solutions
,Summary
,Exam
,Viva Questions
;
NCERT Exemplar: Limits and Derivatives Free PDF Download
Importance of NCERT Exemplar: Limits and Derivatives
NCERT Exemplar: Limits and Derivatives Notes
NCERT Exemplar: Limits and Derivatives Commerce Questions
Study NCERT Exemplar: Limits and Derivatives on the App
|
© EduRev
|
Education Revolution
|
|
