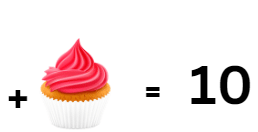Class 5 Maths - Can you see the pattern - CBSE Worksheets Solutions - 1
Q1: Complete Pattern:
(i) Look at the following pattern and fill in the missing number.
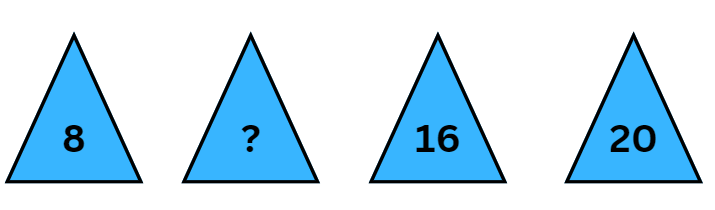
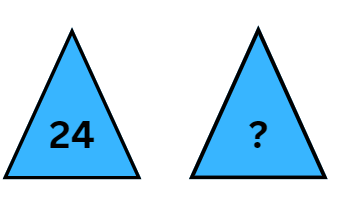
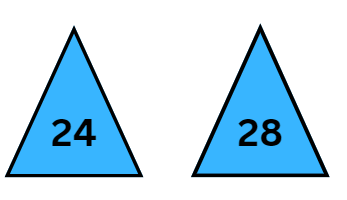
Ans: 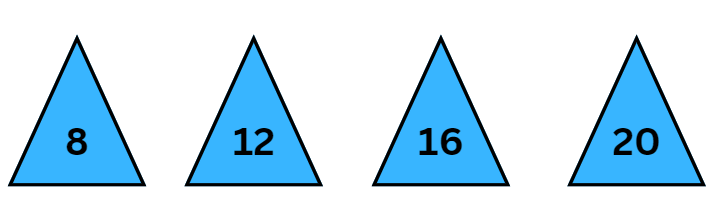
Step 1: Analyze the differences between the known numbers
The difference between 16 and 20 is +4.
The difference between 20 and 24 is +4.
This suggests that the numbers are increasing by 4.
Step 2: Apply the Pattern Backwards
If we go backwards from 16, subtracting 4:
16−4=12
So, the missing number before 16 is 12.
Step 3: Apply the Pattern Forwards
From 24, if we add 4:
24+4=28
So, the missing number after 24 is 28.
The missing numbers are 12 and 28.
The complete sequence is:
8, 12, 16, 20, 24, 28.
(ii) Find the next number in the pattern:
5, 10, 15, 20, 25, ___, ___.
Ans: 30, 35
The pattern in the sequence is that each number increases by 5.
Starting from 5:
5 + 5 = 10
10 + 5 = 15
15 + 5 = 20
20 + 5 = 25Following this pattern:
25 + 5 = 30
30 + 5 = 35
(iii) Complete the pattern:
3, 33, 333, ___, ___.
Ans: 3333, 33333
The pattern in the sequence is that each number consists of the digit 3 repeated one more time than the previous number:
3, 33, 333
Following this pattern, the next numbers would be:
3333 (four 3s), 33333 (five 3s)
So, the completed pattern is 3333 and 33333.
(iv) Identify the pattern and fill in the missing letters.
D, F, H, ___, ___, N
Ans: J, L
The pattern involves skipping one letter between each entry:
D (skip E) → F
F (skip G) → H
H (skip I) → J
J (skip K) → L
L (skip M) → N
The correct missing letters are J and L.
The complete sequence is: D, F, H, J, L, N.
(v) A tree produced 3 apples on Monday, 4 apples on Tuesday, 5 apples on Wednesday, and the pattern continued. How many apples did it produce on Friday?
Ans: 7 apples
The pattern shows that the tree produced one more apple each day:
Monday: 3 apples
Tuesday: 4 apples
Wednesday: 5 apples
Thursday: 6 apples (continuing the pattern)
Following this pattern, for Friday:
Friday: 7 apples
So, the tree produced 7 apples on Friday.
(vi) Can you fill in the missing numbers in the ladder?

Ans: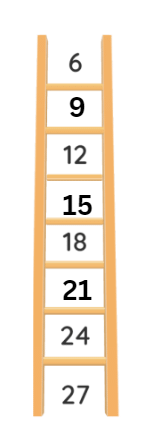
The pattern in the ladder is that each number increases by 3.
i.e., 6 + 3 = 9
9 + 3 = 12
12 + 3 = 15
15 + 3 = 18
18 + 3 = 21 and so on.
(vii) Complete the Series.
a, e, ____, o, u
Ans: i
As these are all vowels. So, a, e, i, o, u.
So the correct answer is i.
(viii) A baker made 4 cupcakes on the first day, 7 cupcakes on the second day, and 10 cupcakes on the third day. If this pattern continues, how many cupcakes will he make on the fourth day?
Ans: 13 cupcakes on the fourth day.
( 1st day)
(2nd day)
i.e, 7 - 4 = 3 & 10 - 7 = 3
So, 10 + 3 = 13
Therefore, on fourth day, there are 13 cupcakes on the fourth day.
Q2: Draw the next figure to complete the Pattern:
(i) 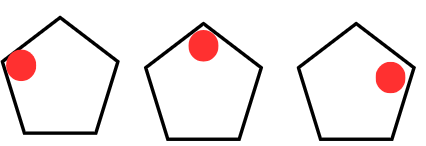 ?
?
Ans: 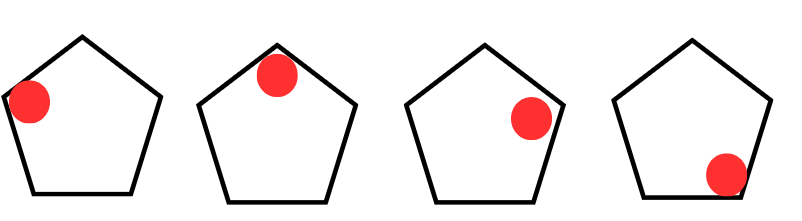
The red circle is moving in clockwise direction.
(ii) 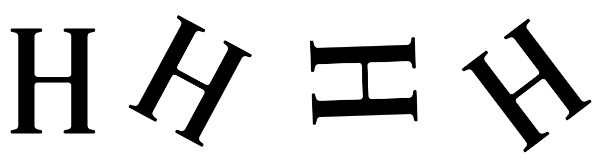 ?
?
Ans: 
The letter H is moving in Clockwise Direction.
(iii) 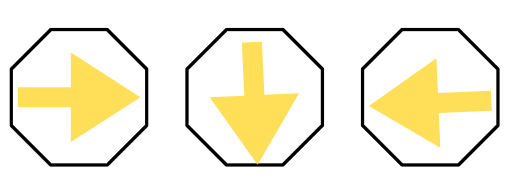 ?
?
Ans: 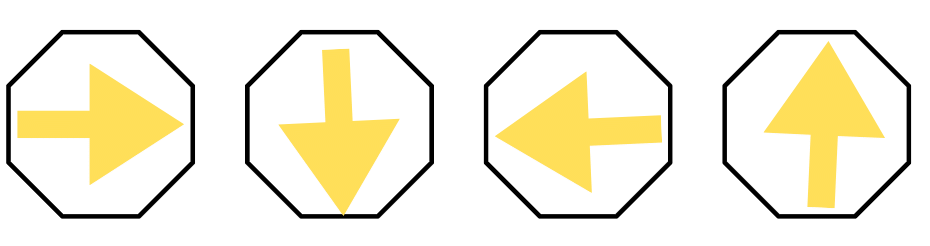
Arrow moving in anticlockwise direction
Q3: Short Answer Type Questions.
(i) Write the greatest odd number formed by the digits 2, 8 and 5.
Ans: 825
To form the greatest odd number using the digits 2, 8, and 5, we need to ensure that the last digit is odd (either 5). The largest arrangement of the remaining digits (2 and 8) will be placed before it. So, the greatest odd number is 825.
(ii) Write the smallest even number formed by the digits 4, 3, 1 and 6.
Ans: 1,346
To form the smallest even number using the digits 4, 3, 1, and 6, we need to ensure that the last digit is even (either 4 or 6).
If we use 4 as the last digit, we get:The smallest arrangement of the remaining digits (1, 3, 6) is 136. This gives us 1364.
If we use 6 as the last digit, we get:
The smallest arrangement of the remaining digits (1, 3, 4) is 134. This gives us 1346.
Comparing the two, the smallest even number is 1346.
(iii) Write the greatest even number formed by the digits 5, 7, 6 and 1.
Ans: 7,516
To form the greatest even number using the digits 5, 7, 6, and 1, we need to use an even digit as the last digit. In this case, the only even digit is 6.
Arranging the remaining digits (5, 7, and 1) in descending order gives us: 7, 5, 1.
Putting it all together, the greatest even number is 7516.
(iv) Write all possible odd numbers formed by the digits 3, 6 and 2.
Ans: 263, 623
To form odd numbers using the digits 3, 6, and 2, the last digit must be odd. The only odd digit available is 3.
The other digits (2 and 6) can be arranged in front of 3. Here are all possible combinations: 263 & 623
So, the possible odd numbers formed are 263 and 623.
(v) Write all possible even numbers formed by the digits 6, 1 and 8.
Ans: 168, 186, 618, 816
To form even numbers using the digits 6, 1, and 8, we need to ensure that the last digit is even. The even digits available are 6 and 8.
Here are all possible combinations for each case:
Ending with 6: 186 & 816
Ending with 8: 168 & 618
So, the possible even numbers formed are 186, 816, 168, and 618.
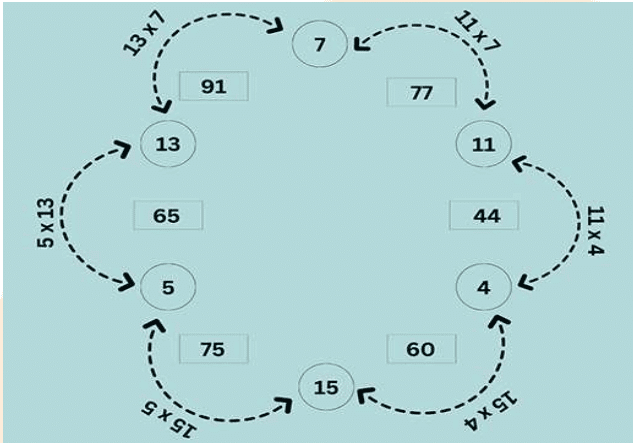
Q4: You will get the number in each bracket by multiplying the number on both side on the box.
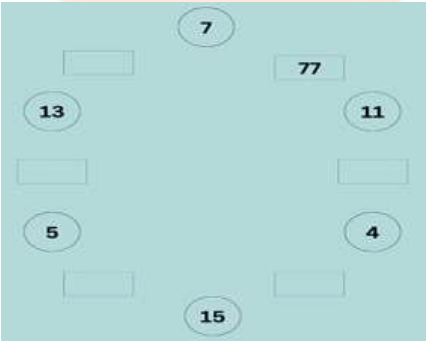
Ans: You will get the number in each bracket by multiplying the number on both sides of the box.
|
31 videos|286 docs|45 tests
|
FAQs on Class 5 Maths - Can you see the pattern - CBSE Worksheets Solutions - 1
| 1. What are some common patterns students might encounter in Class 5 math? |  |
| 2. How can I help my child understand patterns better? |  |
| 3. What is the importance of learning patterns in math? |  |
| 4. Are there any specific exercises or worksheets that focus on patterns for Class 5? |  |
| 5. How can patterns be applied in real-life situations? |  |