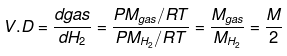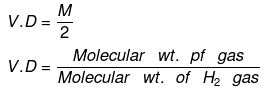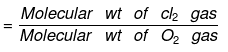Atomic & Molecular Mass and Mole Concept | Chemistry Class 11 - NEET PDF Download
| Table of contents |

|
| Atom and Atomic Weight |

|
| Average Atomic Mass |

|
| The Molecule & Molecular Mass |

|
| Molar Mass |

|
| Formula Mass |

|
| Mole Concept |

|
| Methods of Calculations of Mole |

|
| Density |

|
Atom and Atomic Weight
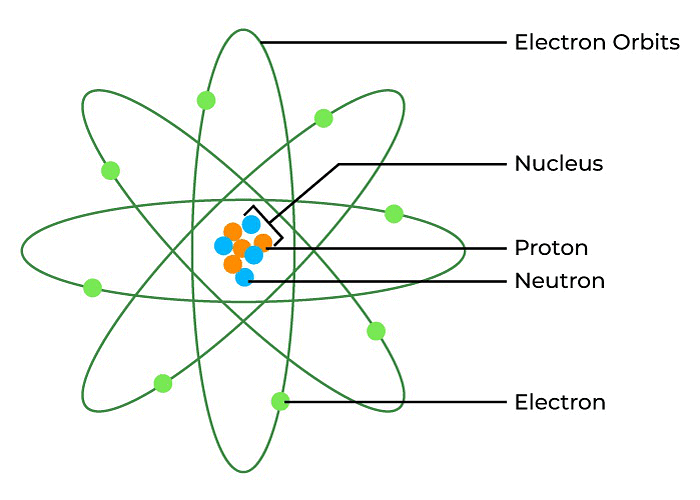 Structure of Atom
Structure of Atom
Note: This picture is just for explanatory purpose , the structure of an atom is much more complex and includes, shells, subshells, orbitals and more.
- The smallest particle of an element that takes part in a chemical reaction is called an atom.
- An atom is so minute that it cannot be detected even with the most powerful microscope, let alone placed on a balance pan and weighed. So, there is no question of determining the absolute weight of an atom.
- So, a new unit for the measurement of masses of atoms was required. Scientists called it the Atomic mass unit. (Amu) or (u).
- Since at that time, such sensitive and complex instruments like the mass spectrometer that we have today did not exist, it was not possible to know the exact mass of any atom.
- So, chemists decided to determine the relative masses of atoms (i.e., how many times one atom of an element is heavier than another).
- Hydrogen atom was first selected as standard as it was found to be the lightest and every other atom would be heavier than H by a certain amount.
- Hence the atomic mass of H was arbitrarily set to be 1
- The atomic weight of an element is:

- When we state that the atomic weight of chlorine is 35.5, we mean that an atom of chlorine is 35.5 times heavier than an atom of hydrogen. It was later felt that the standard for reference should be changed as Hydrogen had 3 isotopes and comparing different isotopes to the element would create a lot of confusion.
- Oxygen was then chosen instead the advantage being that the atomic weights of most other elements became close to whole numbers.
- The atomic weight of an element is:

- The modern reference standard for atomic weights is the carbon isotope of mass number 12.
- The atomic weight of an element is:

- On this basis, atomic weight of oxygen 16 was changed to 15.9994.
- Nowadays atomic weight is called relative atomic mass and denoted by amu (atomic mass unit). The standard for atomic mass is C12.
- Atomic weight is not a weight but a number. Atomic weight is not absolute but relative to the weight of the standard reference element (C12). So it must be unitless.
- Gram atomic weight is atomic weight expressed in grams, but it has a special significance with reference to a mole which is that mass of 1 mole of atoms, 6.022*10 23 atoms weigh equal to their atomic mass in g.
- One atomic mass unit is defined as a mass exactly equal to one-twelfth of the mass of one carbon-12 atom and 1 amu = 1.66056 × 10–24 g
 AMU versus GRAMS
AMU versus GRAMS
Relationship between gram and amu:
⇒ 1 amu = 1/12 wt of one C-12 atom
⇒ For C, 1 mole C = 12 gm = 6.023 × 1023 atoms or wt. of 6.023 × 1023 atoms = 12 gm
⇒ wt. of 1 atom of C = 12/NA gm (NA → Avogadro's number = 6.23 × 1023)
⇒ 1 amu = 1/12 wt of one C-12 atom
⇒ 1 amu = 1/12 × 12/NA gm
⇒ 1 amu = 1/NA g
So, 1 amu = 1.66 × 10-24 g
1 amu = 1.66 × 10-27 kg
Today, ‘amu’ has been replaced by ‘u’ which is known as unified mass.
When we use atomic masses of elements in calculations, we actually use average atomic masses of elements which are explained below.
Mass of an atom of hydrogen = 1.6736 × 10-24 g
Thus, in terms of amu, the mass of a hydrogen atom is:
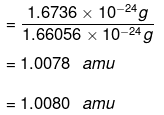
Average Atomic Mass
- Many naturally occurring elements exist as more than one isotope. When we take into account the existence of these isotopes and their relative abundance (percent occurrence), the average atomic mass of that element can be computed as:
(exact weight of isotope 1) * (% abundance of isotope 1) + (exact weight of isotope 2) * (abundance of isotope 2) = Average atomic weight of the element
Example: Carbon has the following three isotopes with relative abundances and masses as shown against each of them.
From the above data, the average atomic mass of carbon will come out to be:(0.98892) (12 u) + (0.01108) (13.00335 u) + (2 ×10–12) (14.00317 u) = 12.011 u - Elements are found in different isotopic forms (atoms of same elements having different atomic mass), so the atomic mass of any element is the average of all the isotopic mass within a given sample.
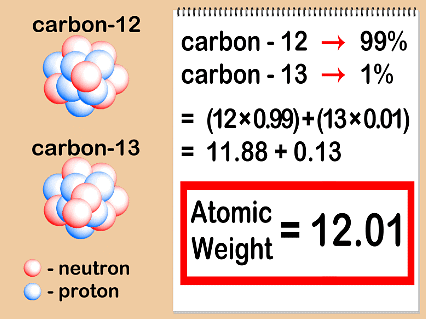
Solved Examples
Example 1. Use the date given in the following table to calculate the molar mass of naturally occurring argon.

Solution. Molar mass of Ar = 35.96755 × 0.071 + 37.96272 × 0.163 + 39.96924 × 0.766
= 39.352 g mol−1
Example 2. Carbon occurs in nature as a mixture of carbon 12 and carbon 13. The average atomic mass of carbon is 12.011. What is the percentage abundance of carbon 12 in nature?
Solution. Average atomic mass is:
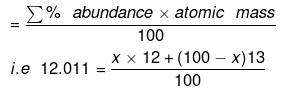
1201.1 = 12x + 1300 – 13x
x = 1300 – 1201.1 = 98.9%
Example 3. Nitrogen is made up of two isotopes, N-14 and N-15. Given nitrogen's atomic weight of 14.007, what is the percent abundance of each isotope?
Solution. (14.003074) (x) + (15.000108) (1 - x) = 14.007
Notice that the abundance of N-14 is assigned 'x' and the N-15 is 'one minus x.' This is the "trick" refered to above. The two abundances always add up to one (or, if you prefer, 100%)
For example, I might have this:
(14) (x) + (15) (1 - x) = 14.007
14x + 15 - 15x = 14.007
x = 15 - 14.007 = 0.993 & 1 - x = 0.007
Example 4. Copper is made up of two isotopes, Cu-63 (62.9296 amu) and Cu-65 (64.9278 amu). Given copper's atomic weight of 63.546, what is the percent abundance of each isotope?
Solution. (62.9296) (x) + (64.9278) (1 - x) = 63.546
Once again, notice that 'x' and 'one minus x' add up to one.
Now solve for x:
x = 0.6915 (the decimal abundance for Cu-63)
The Molecule & Molecular Mass
- Avogadro (1811) suggested that the fundamental chemical unit is not an atom but a molecule, which may be a cluster of atoms held together in some manner causing them to exist as a unit. The term molecule means the smallest particle of an element or a compound that can exist freely and retain all its properties.
- The molecular mass of a substance is an additive property and can be calculated by adding the atomic masses of all the atoms of different elements present in one molecule.
Molar Mass
Relative Molar Mass is defined as the smallest mass unit of a compound with one-twelfth of the mass of one carbon – 12 atom.
Molecular Mass of Sugar (Sucrose)
Molecular mass C12H22O11 = 12(mass of C) + 22(mass of H) + 11(mass of O)
Molecular mass C12H22O11 = 12(12) + 22(1) + 11(16)
Molecular mass C12H22O11 = 342g/mol
One can use the following methods to find the Molecular weight:
(a) Vapour Density Method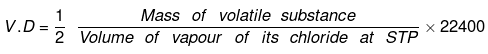 Molecular mass = 2 × V.D.
Molecular mass = 2 × V.D.
(b) Diffusion Method: According to Graham’s law of diffusion, rate of diffusion of a gas is inversely proportional to the square root of its molecular mass.
 (c) Victor Meyer Method: This method applies to volatile organic liquids. Suppose vapour of an organic liquid having mass W g occupies a volume of V mL at STP. Then its molecular mass is:
(c) Victor Meyer Method: This method applies to volatile organic liquids. Suppose vapour of an organic liquid having mass W g occupies a volume of V mL at STP. Then its molecular mass is: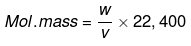
Formula Mass
- Some substances such as sodium chloride do not contain discrete molecules as their constituent units. In such compounds, positive (sodium) and negative (chloride) entities are arranged in a three-dimensional structure. It may be noted that in sodium chloride, one Na+ is surrounded by six Cl– and vice-versa.
- The formula such as NaCl is used to calculate the formula mass instead of molecular mass as in the solid-state sodium chloride does not exist as a single entity.
Thus, formula mass of sodium chloride = atomic mass of sodium + atomic mass of chlorine
= 23.0 u + 35.5 u
= 58.5 u
Mole Concept
- A mole is an amount unit similar to familiar units like pair, dozen, gross, etc. It provides a specific measure of the number of atoms or molecules in a bulk sample of matter.
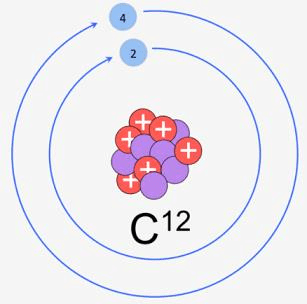
- One mole is defined as the amount of substance containing the same number of discrete entities (atoms, molecules, ions, etc.) as the number of atoms in a sample of pure 12 C weighing exactly 12 g.
 C-12 Isotope
C-12 Isotope - In order to determine this number precisely, the mass of a carbon-12 atom was determined by a mass spectrometer and found to be equal to 1.992648 × 10–23 g. Knowing that one mole of carbon weighs 12 g, the number of atoms in it:

- The number of entities composing a mole has been experimentally determined to be 6.0221367 × 1023, a fundamental constant named Avogadro’s number (NA) or the Avogadro constant in honor of Italian scientist Amedeo Avogadro.
- This constant is properly reported with an explicit unit of “per mole,” a conveniently rounded version being 6.022×1023/mol.
- It may be emphasized that the mole of a substance always contains the same number of entities, no matter what the substance may be.
1 mole = collection of 6.02 × 1023 species
6.02 × 1023 = NA = Avogadro's No. - 1 mole of atoms is also termed as 1 gm-atom, 1 mole of ions is termed as 1 gm-ion and 1 mole of a molecule termed as 1 gm-molecule.
Methods of Calculations of Mole
(a) If no. of some species is given, then no. of moles is: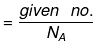
(b) If the weight of a given species is given, then no of moles is:
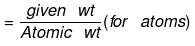 or
or 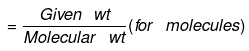
(c) If the volume of a gas is given along with its temperature (T) and pressure (P)
use: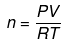
where R = 0.0821 liter-atm/mol-K (when P is in atmosphere and V is in litre.)
Note:
1 mole of any gas at STP (0°C & 1 bar) occupies 22.7 litres.
1 mole of any gas at STP (0°C & 1 atm) occupies 22.4 litres.
A mole of any substance is related to:
- Number of particles
- Mass of a substance
- Volume of the gaseous substance
1. Mole-Particle Relationship
- A mole is a collection of 6.023 × 1023 particles, ions, atoms etc.
- Avogadro Number (NA): The number of carbon atoms present in one gram-atom (1-mole atom) of C-12 isotope is called Avogadro’s number.
- One gram-atom (12 grams) of C–12 contains 6.02 × 1023 atoms. Thus the numerical value of Avogadro’s number (NA) is 6.02 × 1023 per mol.
- It should be noted that 1 a.m.u.= 1/12 th of mass of a Carbon-12 atom.
 (i) 6.023 × 1023 atoms of Na constitute one-mole atom of Na.
(i) 6.023 × 1023 atoms of Na constitute one-mole atom of Na.
(ii) 6.023 × 1023 molecules of oxygen constitute 1 mole of oxygen molecules.
(iii) 6.023 × 1023 electrons constitute one mole of electrons.
(iv) No. of moles = Number of particles/6.023 × 1023
2. Mole-Weight Relationship
- One mole of every substance weighs equal to the gram atomic weight of the substance or to the gram molecular weight of the substance.
Example: (i) 1 mole of sodium weighs 23 g of Na.
(ii) 1 mole of CaCO3 weighs 100 g.
Number of moles = Mass of substance in grams/Mass of weight in grams
3. Mole-Volume Relationship
- One mole of every gas occupies 22.4 lit. of volume at STP i.e. 1 mole of O2 occupies 22400 ml of volume at STP.
- 1 mole of He occupies 22400 ml of volume at STP.
- Number of moles = 'V' of gas in litres at STP/22.4
 Mole Concept
Mole Concept
Elemental Analysis
- For 'n' mole of a compound (C3H7O2)
- Moles of C = 3n
- Moles of H = 7n
- Moles of O = 2n
Density
Density is of two types:
(a) Absolute density
(b) Relative density

Vapor Density
- It is defined only for gas. It is a density of gas with respect to H2 gas at the same temp & pressure.


- The density of Cl2 gas with respect to O2 gas is:

Solved Examples
Example 1. Find the weight of water present in 1.61 g of Na2SO4. 10H2O
Solution. Moles of Na2SO4.10H2O 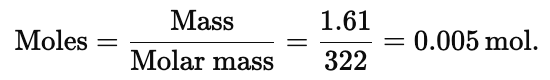
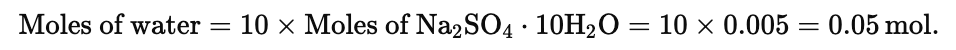
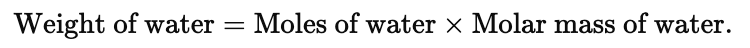
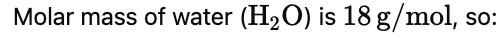
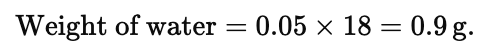 Example 2. A molecule of a compound has 13 carbon atoms, 12 hydrogen atom, 3 oxygen atoms and 3.02 × 10-23 gm of other element. Find the molecular wt. of compound.
Example 2. A molecule of a compound has 13 carbon atoms, 12 hydrogen atom, 3 oxygen atoms and 3.02 × 10-23 gm of other element. Find the molecular wt. of compound.
Solution. Wt. of the 1 molecule of a compound = 13 × 12 × 3 × 3.02 × 10-23
= 234.18 / NA = 234 amu.
Example 3. Calculate the number of moles of electron present in 1 kg of it. (me = 9.1 × 10–31 kg)
Solution. Number of electrons in 1 kg = 1 kg/9.1 × 10-31 kg
Number of moles = Number of particles/6.023 × 1023
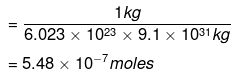
Example 4. What will be the number of moles in 13.5 g of SO2Cl2?
Solution. Molecular mass of SO2Cl2 = 32 + 32 + 71 = 135 g mol–1
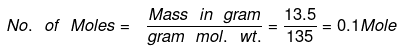
Example 5. What will be the number of moles of oxygen in one litre of air containing 21% oxygen by volume under STP conditions?
Solution. 100 ml of air at STP contains 21 ml of O2
1000 ml of air at STP contains = 21/100 × 1000 = 210 ml O2
∴ No. of moles = Volume in ml under STP conditions/22400 litre
= 210/22400 = 9.38 × 10-3 mole.
Example 6. Calculate the mass of (i) an atom of silver (ii) a molecule of carbon dioxide.
Solution. (i) 1 mole of Ag atoms = 108 g
(∴ Atomic mass of silver = 108u)
= 6.022 × 1023 atoms
6.022 × 1023 atoms of silver have mass = 108g
∴ Mass of one atom of silver
 (ii) 1 mole of CO2 = 44 g
(ii) 1 mole of CO2 = 44 g
(Molecular mass of CO2 = 1 x 12 + 2 x 16 = 44u)
= 6.022 × 1023 molecules
Thus, 6.022 × 1023 molecules of CO2 has mass = 44 g
∴ 1 molecule of CO2 has mass
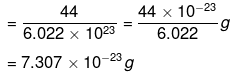
Example 7. Calculate the number of molecules present
(i) In 34.20 grams of cane sugar (C12H22O11).
(ii) In one litre of water assuming that the density of water is 1 g/cm3.
(iii) In one drop of water having mass 0.05 g.
Solution. (i) 1 mole of C12H22O11 = 342 g
[Molecular mass of cane sugar C12H22O11]
= 12 x 12 + 22 × 1 + 11 × 16 = 342 amu
= 6.022 × 1023 molecules
Now 342 g of cane sugar contain 6.022 × 1023 molecules.
∴ 34.2 g of cane sugar will contain
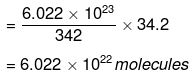
(ii) 1 mole of water = 18 g = 6.022 × 1023 molecules.
Mass of 1 litre of water = Volume × density = 1000 × 1 = 1000 g
Now 18 g of water contains = 6.022 x 1023 molecules.
∴ 1000 g of water will contain 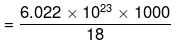 = 3.346 x 1025 molecules
= 3.346 x 1025 molecules
(iii) 1 mole of H2O = 18 g = 6.022 × 1023 molecules.
Mass of 1 drop of water = 0.05 g
Now 18 g of H2O contain = 6.022 × 1023 molecules.
∴ 0.05 g of H2O will contain =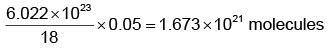
Example 8. Calculate the number of moles in each of the following:
(i) 392 grams of sulphuric acid
(ii) 44.8 litres of carbon dioxide at STP
(iii) 6.022 × 1023 molecules of oxygen
(iv) 9.0 grams of aluminium
(v) 1 metric ton of iron (1 metric ton = 103 kg )
(vi) 7.9 mg of Ca
(vii) 65.5 mg of carbon
Solution.
(i) 1 mole of H2SO4 = 98 g
∵ Molecular mass of H2SO4 = 2 × 1 + 32 + 4 × 16 = 98u)
Thus 98 g of H2SO4 = 1 mole of H2SO4
∴ 392 g of H2SO4
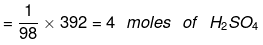
(ii) 1 mole of CO2 = 22.4 litres at STP
i.e. 22.4 litres of CO2 at STP = 1 mole
∴ 44.8 litres of CO2 at STP
= 1/22.4 × 44.8
= 2 moles CO2
(iii) 1 mole of O2 molecules = 6.022 × 1023 molecules
6.022 × 1023 molecules = 1 mole of oxygen molecules
(iv) 1 mole of Al = 27 g of Al
(∴ Atomic mass of aluminium = 27 g)
i.e. 27 g of aluminium = 1 mole of Al

(v) 1 metric ton of Fe = 103 kg = 106 g
1 mole of Fe = 56 g of Fe
∴ 106 g of Fe = 106/56 molecules
= 1.786 × 104 moles
(vi) 7.9 mg of Ca = 7.9 × 10−3 g of Ca

(vii) 65.5 µg of C = 65.5 10-6 g of C
Try Yourself!
Q.1. Find the weight of 6023 molecules of CO2 in grams.
Ans. 4.4 × 10–19 gm
Q.2. Calculate the total number of electrons present in 1.6 g of methane. (Molecular wt. of methane = 16 a.m.u.)
Ans. 6.023 × 1023 electrons
Q.3. 0.24 gm of a volatile substance upon vaporization gives 45 ml vapours at STP. What will be the vapour density of the substance?
Ans. 59.73
Q.4. What is the mass of carbon present in 0.5 moles of K4[Fe(CN)6]?
Ans. 36 gm
Q.5. Calculate how many methane molecules and how many hydrogen and carbon atoms are there in 25.0 g of methane.
Ans. 9.41 × 1023 CH4 molecules, 9.41 × 1023 carbon atoms, and 37.64 × 1023 hydrogen atoms.
Q.6. One litre of gas at NTP weighs 1.97g. Find the molecular mass of gas.
Ans. 44.128 g
|
129 videos|244 docs|88 tests
|
FAQs on Atomic & Molecular Mass and Mole Concept - Chemistry Class 11 - NEET
| 1. What is the difference between atomic weight and average atomic mass? |  |
| 2. How is molar mass different from molecular mass? |  |
| 3. What is the formula mass and how is it calculated? |  |
| 4. How is the concept of mole used in chemistry calculations? |  |
| 5. What are some common methods used to calculate the number of moles in a sample? |  |

|
Explore Courses for NEET exam
|

|
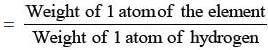

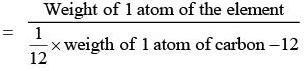




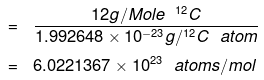
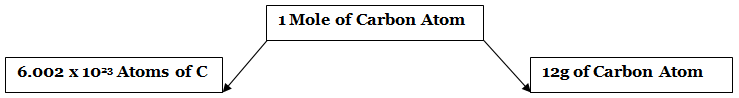 (i) 6.023 × 1023 atoms of Na constitute one-mole atom of Na.
(i) 6.023 × 1023 atoms of Na constitute one-mole atom of Na.