NCERT Exemplar: Sets- 2 | Mathematics (Maths) Class 11 - Commerce PDF Download
OBJECTIVE TYPE QUESTIONS
Q.29. Suppose A1, A2, …, A30 are thirty sets each having 5 elements and B1, B2, …, Bn are n sets each with 3 elements. Let 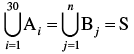
and each element of S belongs to exactly 10 of the Ai’s and exactly 9 of the Bj’s then n is equal to
(a) 15
(b) 30
(c) 45
(d) None
Ans. (c)
Solution.
Number of elements in A1 A2 A3 …A30 = 30×5 = 150 (when repetition is not allowed)
But each element is repeated 10 times
∴ n(S) = 30 × 5/10 = 150/10 = 15 .........(i)
Number of elements in B1 B2 B3 … Bn = 3n (when repetition is not allowed)
But each element is repeated 09 times
∴ n(S) = 3n/9 = n/3 ...........(ii)
From(i) and (ii) we get
n/3 = 15
⇒ n = 15 × 3 = 45
Hence, the correct option is (c).
Q.30. Two finite sets have m and n elements. The number of subsets of the first set is 112 more than that of the second set. The values of m and n are, respectively,
(a) 4, 7
(b) 7, 4
(c) 4, 4
(c) 7, 7
Ans. (b)
Solution.
We have the number of subsets of set containing n elements = 2n
So, according to the question, we have
2m – 2n = 112
⇒ 2n.(2m – n – 1) = 24.7
∴ 2n = 24 and 2m–n– 1 = 7
⇒ n = 4 and 2m – n = 1 + 7 = 8 = 23
⇒ n = 4 and m – n = 3
⇒ m – 4 = 3
⇒ m = 7
Hence,the correct option (b).
Q.31. The set (A ∩ B′)′ ∪ (B ∩ C) is equal to
(a) A′ ∪ B ∪ C
(b) A′ ∪ B
(c) A′ ∪ C′
(d) A′ ∩ B
Ans. (b)
Solution.
we know that: (A ∩ B)’ = A’ ∪ B’ [De Morgan's law]
∴ (A ∩ B’)’ ∪ (B ∩ C) = [A’ ∪ (B’)’] ∪ (B ∩ C)
= (A’ ∪ B) ∪ (B ∩ C) [∵ (B’)’ = B]
= A’ ∪ B
Hence, the correct option is (b)
Q.32. Let F1 be the set of parallelograms, F2 the set of rectangles, F3 the set of rhombuses, F4 the set of squares and F5 the set of trapeziums in a plane. Then F1 may be equal to
(a) F2 ∩ F3
(b) F3 ∩ F4
(c) F2 ∪ F5
(d) F2 ∪ F3 ∪ F4 ∪ F1
Ans. (d)
Solution.
We know that rectangles, rhombus and square in a plane is a parallelogram but trapezium is not a parallelogram.
∴ F1 = F2 ∪ F3 ∪ F4 ∪ F1
Hence,the correct option is (d).
Q.33. Let S = set of points inside the square, T = the set of points inside the triangle and C = the set of points inside the circle. If the triangle and circle intersect each other and are contained in a square. Then
(a) S ∩ T ∩ C = φ
(b) S ∪ T ∪ C = C
(c) S ∪ T ∪ C = S
(d) S ∪ T = S ∩ C
Ans. (c)
Solution.
The given conditions of the question may be represented by the following Venn diagram. From the given Venn diagram, we clearly conclude that
S ∪ T ∪ C = S
Hence, the correct option is (c).
Q.34. Let R be set of points inside a rectangle of sides a and b (a, b > 1) with two sides along the positive direction of x-axis and y-axis. Then
(a) R = {(x, y) : 0 ≤ x ≤ a, 0 ≤ y ≤ b}
(b) R = {(x, y) : 0 ≤ x < a, 0 ≤ y ≤ b}
(c) R = {(x, y) : 0 ≤ x ≤ a, 0 < y < b}
(d) R = {(x, y) : 0 < x < a, 0 < y < b}
Ans. (d)
Solution.
Let OABC be a rectangle whose sides a and b are along the positive direction of X
and Y respectively.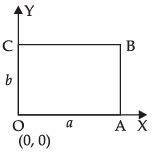
∴ Clearly,
R = {(x, y) : 0 < x < a and 0 < y < b}
Hence, the correct option is (d).
Q.35. In a class of 60 students, 25 students play cricket and 20 students play tennis, and 10 students play both the games. Then, the number of students who play neither is
(a) 0
(b) 25
(c) 35
(d) 45
Ans. (b)
Solution.
Total number of students = 60
⇒ n(U) = 60
Number of students who play cricket = 25
⇒ n(C) = 25
Number of students who play tennis = 20
⇒ n(T) = 20
Number of students who play cricket and tennis both = 10
⇒ n(C ∩ T) = 10
∴ n(C ∪ T) = n(C) + n(T) – n(C ∩ T)
= 25 + 20 – 10 = 45 – 10 = 35
∴ n(C’ ∩ T’) = n(U) – n(C ∪ T)
= 60 – 35 = 25
Hence, the correct option is (b).
Q.36. In a town of 840 persons, 450 persons read Hindi, 300 read English and 200 read both. Then the number of persons who read neither is
(a) 210
(b) 290
(c) 180
(d) 260
Ans. (b)
Solution.
Total number of persons in a town = 840
⇒ n(U) = 840
Number of persons who read Hindi = 450
⇒ n(H) = 450
Number of persons who read English = 300
⇒ n(E) = 300
Number of persons who read both = 200
⇒ n(H ∩ E) = 200
∴ n(H ∪ E) = n(H) + n(E) – n(H ∩ E)
= 450 + 300 – 200 = 550
n(H’ ∩ E’) = n(U) – n(H ∪ E)
= 840 – 550 = 290
Hence, the correct option is (b).
Q.37. If X = {18n - 7n - 1| n ∈ N} and Y= {49n - 49 | n ∈ N}, then
(a) X ⊂ Y
(b) Y ⊂ X
(c) X = Y
(d) X ∩ Y = Φ
Ans. (a)
Solution.
Given that: X = {8n - 7n - 1 |n ∈ N} = {0, 49, 490, ...}
And Y = {49n - 49 | n ∈ N} = {0, 49, 98, ...}
Here, it is clear that every element belonging to X is also present in Y.
∴ X ⊂ Y. Hence, the correct option is (a).
Q.38. A survey shows that 63% of the people watch a News Channel whereas 76% watch another channel. If x% of the people watch both channel, then
(a) x = 35
(b) x = 63
(c) 39 ≤ x ≤ 63
(d) x = 39
Ans. (c)
Solution.
Let p% of the people watch a channel and q% of the people watch another channel
∵ n(p ∩ q) = x% and n(p ∪ q) ≤ 100
So, n(p ∪ q) ≥ n(p) + n(q) – n(p ∩ q)
100 ≥ 63 + 76 – x
100 ≥ 139 – x
⇒ x ≥ 139 – 100
⇒ x ≥ 39
Now n(p) = 63
∴ n(p ∩ q) ≤ n(p)
⇒ x ≤ 63
So 39 ≤ x ≤ 63.
Hence, the correct option is (c).
Q.39. If sets A and B are defined as
A = {(x, y) | y = 1/x, 0 ≠ x ∈ R}
B = {(x, y) | y = – x, x ∈ R}, then
(a) A ∩ B = A
(b) A ∩ B = B
(c) A ∩ B = φ
(d) A ∪ B = A
Ans. (c)
Solution.
Give that: A = {(x, y) | y = 1/x, 0 ≠ x ∈ R},
and B = {(x, y)|y = – x, x ∈ R}
It is very clear that y = 1/x and y = – x
∵ 1/x ≠ -x
∴ A ∩ B = ϕ
Hence, the correct option is (c).
Q.40. If A and B are two sets, then A ∩ (A ∪ B) equals
(a) A
(b) B
(c) φ
(d) A ∩ B
Ans. (a)
Solution.
Given that: A ∩ (A ∪ B)
Let x ∈ A ∩ (A ∪ B)
⇒ x ∈ A and x ∈ (A ∪ B)
⇒ x ∈ A and (x ∈ A or x ∈ B)
⇒ (x ∈ A and x ∈ A)or (x ∈ A and x ∈ B)
⇒ x ∈ A or x ∈ (A ∩ B)
⇒ x ∈ A.
Hence the correct option is (a)
Q.41. If A = {1, 3, 5, 7, 9, 11, 13, 15, 17} B = {2, 4, ..., 18} and N the set of natural numbers is the universal set, then A′ ∪ (A ∪ B) ∩ B′) is
(a) φ
(b) N
(c) A
(d) B
Ans. (b)
Solution.
Given that:
A = {1, 3, 5, 7, 9, 11, 13, 15, 17}
B = {2, 4, …, 18}
U= N = {1, 2, 3, 4, 5, …}
A’ ∪ (A ∪ B) ∩ B’ = A’ ∪ [(A ∩ B’) ∪ (B ∩ B’)]
= A’ ∪ (A ∩ B’) ∪ Φ [∵ A ∩ A’ = Φ]
= A’ ∪ (A ∩ B’)
= (A’ ∪ A) ∩ (A’ ∪ B’)
= N ∪ (A’ ∪ B’) [∵ A’ ∪ A = N]
= A’ ∪ B’
= (A ∩ B)’ = (Φ)’ = N [∵ A ∩ B = Φ]
Hence, the correct option is (b).
Q.42. Let S = {x | x is a positive multiple of 3 less than 100} P = {x | x is a prime number less than 20}. Then n(S) + n(P) is
(a) 34
(b) 31
(c) 33
(d) 30
Ans. (b)
Solution.
Given that: S ={x|x is a positive multiple of 3 < 100}
∴ S = {3, 6, 9, 12, 15, 18,…, 99}
⇒ n(S) = 33
T = (x | x is a prime number < 20}
∴ T = {2, 3, 5, 7, 11, 13, 17, 19}
⇒ n(T) = 8
So, n(S) + n(T) = 33 + 8 = 41
Hence, the correct option is (b).
Q.43. If X and Y are two sets and X′ denotes the complement of X, then X ∩ (X ∪ Y)′ is equal to
(a) X
(b) Y
(c) φ
(d) X ∩ Y
Ans. (c)
Solution.
Let x ∈ X ∩ (X ∪ Y)′
⇒ x ∈ X ∩ (X’ ∩ Y’)
⇒ x ∈ (X ∩ X’) ∩ (X ∩ Y’)
⇒ x ∈ Φ ∩ (X ∩ Y’) [∵A ∩ A’ = Φ]
⇒ x ∈ Φ
Hence, the correct option is (c).
Fill in the blanks
Q.44. The set {x ∈ R : 1 ≤ x < 2} can be written as ______.
Ans.
The set {x ∈ R : 1 ≤ x < 2} can be written as [1, 2)
Hence, the filler is [1, 2).
Q.45. When A = φ, then number of elements in P(A) is ______.
Ans.
Here A = Φ
∴ n(A)=0
∵ n[P(A)]= 2n(A)
= 20 = 1
Hence, the filler is 1.
Q.46. If A and B are finite sets such that A ⊂ B, then n (A ∪ B) = ______.
Ans.
Since A ⊂ B
∴ n(A ∪ B) = n(B)
Hence, the filler is n(B).
Q.47. If A and B are any two sets, then A – B is equal to ______.
Ans.
From the Venn diagram it is clear that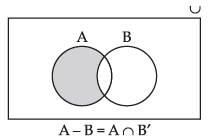
A – B = A ∩ B’.
Hence the filler is A ∩ B’.
Q.48. Power set of the set A = {1, 2} is _______.
Ans.
Power set of A = P(A)
= {{1}, {2}, {1, 2}, Ф}
Hence, the filler is {{1}, {2}, {1, 2}, Ф }.
Q.49. Given the sets A = {1, 3, 5}. B = {2, 4, 6} and C = {0, 2, 4, 6, 8}. Then the universal set of all the three sets A, B and C can be _______.
Ans.
Given that: A = {1, 3, 5}, B = {2, 4, 6} and C = {0, 2, 4, 6, 8}
∴Universal set of all the given sets is
U = {0, 1, 2, 3, 4, 5, 6, 8}
Hence, the filler is {0, 1, 2, 3, 4, 5, 6, 8}.
Q.50. If U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, A = {1, 2, 3, 5}, B = {2, 4, 6, 7} and C = {2, 3, 4, 8}. Then
(i) (B ∪ C)′ is _______.
(ii)(C – A)′ is _______.
Ans.
Given that: U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, A = {1, 2, 3, 5} B = {2, 4, 6, 7} and C = {2, 3, 4, 8}
(i) (B ∪ C) = {2, 3, 4, 6, 7, 8} = {1, 5, 9, 10}
Hence, the filler is {1, 5, 9, 10}.
(ii) (C - A) = {4, 8} = {1, 2, 3, 5, 6, 7, 9, 10}
Hence, the filler is {1, 2, 3, 5, 6, 7, 9, 10}.
Q.51. For all sets A and B, A – (A ∩ B) is equal to _______.
Ans. Since A – B = A ∩ B’
⇒ A – (A ∩ B)= A ∩ B’
Hence, the filler is A ∩ B’.
Q.52. Match the following sets for all sets A, B and C
Ans.
(i) ((A’ ∪ B’) – A)’ = [(A’ ∪ B’) ∩ A)’]’ [∵ A – B = A ∩ B’]
= [(A ∩ B)’ ∩ A)’]’ [∵ A’ ∪ B’= (A ∩ B)’]
= [(A ∩ B)’]’ ∪ (A’)’ [∵(A’)’ = A]
= (A ∩ B) ∪ A
= A.
So (i) is match with (b).
(ii) [B’ ∪ (B’ – A)]’ = [B’ ∪ (B’ ∩ A’)]’ [∵ A – B = A ∩ B’]
= (B’)’ ∩ (B’ ∩ A’)’ [∵ A’ ∩ B’ = (A ∪ B)’]
= B ∩ (B ∪ A) = B
So (ii) is matched with (c).
(iii) (A – B) – (B – C)
= (A ∩ B’) – (B ∩ C’) [∵A – B = (A ∩ B’)]
= (A ∩ B’) ∩ (B ∩ C’)’
= (A ∩ B’) ∩ (B’ ∩ (C’)’) [(A ∩ B)’ = A’ ∪ B’]
= (A ∩ B’) ∩ (B’ ∩ C)
= [A ∩ (B’ ∪ C)] ∩ [B’ ∩ (B’ ∪ C)]
= [A ∩ (B’ ∪ C)] ∩ B’
= (A ∩ B’) ∩ (B’ ∪ C) ∩ B’
= (A ∩ B’) ∩ B’ = (A ∩ B’)= A – B
So, (iii) is matched with (a).
(iv) (A – B) ∩ (C – B) = (A ∩ B’) ∩ (C ∩ B’) [∵A – B= (A – B’)]
= (A ∩ C) ∩ B’
= (A ∩ C) – B [∵ A ∩ B’ = A – B]
Hence, (iv) is matched with (f).
(v) A × (B ∪ C) = (A × B) ∩ (A × C)
So, (v) is matched with (d).
(vi) A × (B ∪ C) = (A × B) ∪ (A × C)
So, (vi) is matched with (e).
State True or False for the following statements
Q.53. If A is any set, then A ⊂ A
Ans.
Since every set is a subset of itself. So, it is ‘True’.
Q.54. Given that M = {1, 2, 3, 4, 5, 6, 7, 8, 9} and if B = {1, 2, 3, 4, 5, 6, 7, 8, 9}, then B ⊄ M
Ans.
M = {1, 2, 3, 4, 5, 6, 7, 8, 9}
and B = {1, 2, 3, 4, 5, 6, 7, 8, 9}
Since M and B has same elements
∴ M = B, so B ⊄ M is False.
Q.55. The sets {1, 2, 3, 4} and {3, 4, 5, 6} are equal.
Ans.
False, since the two sets do not contain the same elements.
Q.56. Q ∪ Z = Q, where Q is the set of rational numbers and Z is the set of integers.
Ans.
True, since every integer is a rational number.
∴ Z ⊂ Q, so Q ∪ Z = Q.
Q.57. Let sets R and T be defined as
R = {x ∈ Z | x is divisible by 2}
T = {x ∈ Z | x is divisible by 6}. Then T ⊂ R
Ans.
We can written the given sets is Roster form
R = {..., – 8, – 6, – 4, – 2, 0, 2, 4, 6, 8, ...}
and T = {..., – 18, – 12, – 6, 0, 6, 12, 18, ...}
Since every element of T is present in R.
So, T ⊂ R.
Hence, the statement is ‘True’.
Q.58. Given A = {0, 1, 2}, B = {x ∈ R | 0 ≤ x ≤ 2}. Then A = B.
Ans.
Here A = {0, 1, 2}, B is a set having all real numbers from 0 to 2.
So A ≠ B.
Hence, the given statement is ‘False’.
|
75 videos|238 docs|91 tests
|
FAQs on NCERT Exemplar: Sets- 2 - Mathematics (Maths) Class 11 - Commerce
| 1. What are sets in mathematics? |  |
| 2. How are sets represented in mathematical notations? |  |
| 3. What is the cardinality of a set? |  |
| 4. What is the empty set or null set? |  |
| 5. How are sets classified based on their elements? |  |

|
Explore Courses for Commerce exam
|

|

















