Chapter 2 - Polynomials, RD Sharma Solutions - (Part-1) | RD Sharma Solutions for Class 10 Mathematics PDF Download
Page No 2.33
Ques.1. Find the zeros of each of the following quadratic polynomial and verify the relationship between the zeros and their coefficients:
(i) f(x) = x2 − 2x − 8
(ii) g(s) = 4s2 − 4s + 1
(iii) h(t) = t2 − 15
(iv) 6x2 − 3 − 7x
(v) p(x)= x2+ 2√2x − 6
(vi) q(x)= √3x2 +10x +7√3
(vii) f(x)= x2 −(√3 + 1) x + √3
(viii) g(x) = a(x2 + 1) − x(a2 + 1)
(ix) h(s)= 2s2 − (1+2√2)s + √2
(x) f(v) = v2 + 4√3v −15
(xi) p(y) = y2 + (3√5/2)y - 5
(xii) q(y) = 7y2 − (11/3)y - 2/3
Ans.1.
(i) We have,
f(x) = x2 − 2x − 8
f(x) = x2 + 2x − 4x − 8
f(x) = x (x + 2) − 4(x + 2)
f(x) = (x + 2) (x − 4)
The zeros of f(x) are given by
f(x) = 0
x2 − 2x − 8 = 0
(x + 2) (x − 4) = 0
x + 2 = 0
x = −2
Or
x − 4 = 0
x = 4
Thus, the zeros of f(x) = x2 − 2x − 8 are α = −2 and β = 4
Now,
Sum of the zeros = α + β
= (-2) + 4
= -2 + 4
= 2
and
= (-Coefficient of x/Coefficient of x2)
= -(-2/1)
= 2
Therefore, sum of the zeros = -(Coefficient of x/Coefficient of x2)
Product of the zeros = αβ
= -2 x 4
= -8
and
= Constant term/Coefficient of x2
= -8/1
= -8
Therefore,
Product of the zeros = Constant term/Coefficient of x2
Hence, the relationship between the zeros and coefficient are verified.
(ii) Given g(s) = 4s2 - 4s + 1
When have,
g(s) = 4s2 − 4s + 1
g(s) = 4s2 − 2s − 2s + 1
g(s) = 2s (2s − 1) − 1(2s − 1)
g(s) = (2s − 1) (2s − 1)
The zeros of g(s) are given by
g(s) = 0
4s2 - 4s + 1 = 0
(2s - 1)(2s - 1) = 0
(2s - 1) = 0
2s = +1
Or
(2s - 1) = 0
2s = 1
s = (1/2)
Thus, the zeros of g(x) = 4s2 - 4s + 1 are
α = 1/2 and β = 1/2
Now, sum of the zeros = α + β
= (1/2 + 1/2)
= (1+1)/2
= 2/2
= 1
and
= (-Coefficient of x/Coefficient of x2)
= -((-4)/(4))
= 4/4
= 1
Therefore, sum of the zeros = (-Coefficient of x/Coefficient of x2)
Product of the zeros = αβ
= (1/2 x 1/2)
= 1/4
and = Constant term/Coefficient of x2
= 1/4
Therefore, the product of the zeroes = Constant term/Coefficient of x2
Hence, the relation-ship between the zeros and coefficient are verified.
(iii) Given h(t) = t2 - 15
We have,
h(t) = t2 − 15
h(t) = (t)2 − (√15)2
h(t) = (t + √15) (t −√15)
The zeros of h(t) are given by
h(t) = 0
(t − √15) (t + √15) = 0
(t − √15) = 0
t = √15
or
(t + √15) = 0
t = −√15
Hence, the zeros of h(t) are α = √15 and β = −√15
Now,
Sum of the zeros = α + β
= √15 + (-√15)
= √15 - √15
= 0
and = (-Coefficient of x/Coefficient of x2)
= 0/1
= 0
Therefore, sum of the zeros = (-Coefficient of x/Coefficient of x2)
also,
Product of the zeros = αβ
= √15 x -√15
= -15
and,
Constant term/Coefficient of x2
= -15/1
= -15
Therefore, the product of the zeros = Constant term/Coefficient of x2
Hence, The relationship between the zeros and coefficient are verified.
(iv) Given f(x) = 6x2 - 3 - 7x
We have, f(x) = 6x2 - 7x - 3
f(x) = 6x2 - 9x + 2x - 3
f(x) = 3x(2x - 3) + 1(2x - 3)
f(x) = (3x + 1)(2x - 3)
The zeros of f(x) are given by
f(x) = 0
6x2 - 7x - 3 = 0
(3x + 1)(2x - 3) = 0
3x + 1 = 0
3x = -1
x = -1/3
Or
2x - 3 = 0
2x = 3
x = 3/2
Thus, the zeros of f(x) = 6x2 - 7x - 3 are α = -1/3 and β = 3/2.
Now,
Sum of the zeros = α + β
= (-1/3 + 3/2)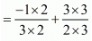
= (-2/6 + 9/6)
=(-2 + 9)/(6)
= 7/6
and, = (-Coefficient of x/Coefficient of x2)
Product of the zeros = α × β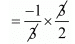
= (-1)/2
and,= Constant term/Coefficient of x2
= (-3)/6
= (-1)/2
Product of zeros = Constant term/Coefficient of x2
Hence, the relation between the zeros and its coefficient are verified.
(v) Given p(x) = x2 + 2√2x - 6
We have,
p(x) = x2 + 2√2x - 6
p(x) = x2 + 3√2x - √2x - 6
p(x) = x(x + 3√2)-√2(x + 3√2)
p(x) = (x - √2)(x + 3√2)
The zeros of p(x) are given by
p(x) = 0
p(x) = x2 + 2√2x - 6
x2 + 2√2x - 6 = 0
(x - √2)(x + 3√2) = 0
(x - √2) = 0
x = √2
Or
(x + 3√2) = 0
x = -3√2
Thus, The zeros of p(x) = x2 + 2√2 - 6 are α = √2 and β = -3√2
Now,
Sum of the zeros = α + β
= √2 - 3√2
= +√2(1 - 3)
= √2(-2)
= -2√2
and, (-Coefficient of x/Coefficient of x2)
= ((-2√2)/(1))
= -2√2
Therefore, Sum of the zeros = (-Coefficient of x/Coefficient of x2)
Product of the zeros = α x β
= √2 x -3√2
= -3 x 2
= -6
and
Constant term/Coefficient of x2
= -6/1
= -6
Therefore, The product of the zeros = Constant term/Coefficient of x2
Hence, the relation-ship between the zeros and coefficient are verified.
(vi) Given q(x) = √3x2 + 10x + 7√3
We have, q(x) = √3x2 + 10x + 7√3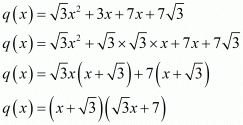
The zeros of g(x) are given by
g(x) = 0
√3x2 + 10x + 7√3 = 0
(x + √3)(√3x + 7) = 0
x + √3= 0
x = -√3
Or
√3 + 7 = 0
√3x = -7
x = (-7)/(√3)
Thus, the zeros of q(x) = √3x2 + 10x + 7√3 are α = -√3 and β = -7/√3
Now,
Sum of the zeros = α + β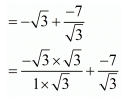

= (-10)/(√3)
and = (-Coefficient of x/Coefficient of x2)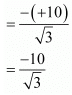
Therefore, sum of the zeros = (-Coefficient of x/Coefficient of x2)
Product of zeros = α × β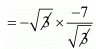
= +7
and = -(Coefficient of x/Coefficient of x2)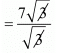
= 7
Therefore, the product of the zeros = Constant term/Coefficient of x2
Hence, the relationship between the zeros and coefficient are verified.
(vii) Given f(x) = x2 - (√3 + 1) + √3
f(x) = x2 - √3x - 1x + √3
f(x) = x(x -√3) -1(x - √3)
f(x) = (x - 1)(x - √3)
The zeros of ƒ(x) are given by
f(x) = 0
x2 - (√3 + 1)x + √3 = 0
(x - 1)(x - √3) = 0
(x - 1) = 0
x = 0 + 1
x = 1
Or
x - √3 = 0
x = 0 + √3
x = √3
Thus, the zeros of x2 - (√3 + 1) are α = 1 and β = √3
Now,
Sum of zeros = α + β
= 1 + √3
= 1 + √3
And,
= (-Coefficient of x/Coefficient of x2)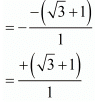
Therefore, sum of the zeros = (-Coefficient of x/Coefficient of x2)
Product of the zeros = αβ
= 1 x √3
= √3
And
= Constant term/Coefficient of x2
= √3/1
= √3
Product of zeros = Constant term/Coefficient of x2
Hence, the relation-ship between the zeros and coefficient are verified.
(viii) Given g(x) = a(x2 + 1) -x(a2 + 1)
g(x) = ax2 -xa2 + a - x
g(x) = xa (x - a) -1 (x - a)
g(x) = (xa - 1)(x - a)
The zeros of g(x) are given by
g(x) = 0
ax2 - (a2 + 1)x + a = 0
xa - 1 =0
xa = 1
x = 1/a
or
x - a = 0
x = a
Thus, the zeros of g(x) = ax2 -(a2 + 1) x + a are
α = 1/a and β = a
Sum of the zeros = α + β
= (1/a) + a
and = (-Coefficient of x/Coefficient of x2)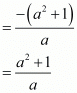
Product of the zeros = α x β
= 1
And, = Constant term/Coefficient of x2
= a/a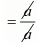
= 1
Therefore,
Product of the zeros = Constant term/Coefficient of x2
Hence, the relationship between the zeros and coefficient are verified.
(ix) h(s) = 2s2 − (1 + 2√2)s + √2
h(s) = 2s2 − s − 2√2s + √2
h(s) = s(2s − 1) − √2(2s − 1)
h(s) = (2s − 1)(s − √2)
The zeros of h(s) are given by
h(s) = 0
2s2 − (1 + 2√2) s + √2 = 0
(2s − 1)(s − √2) = 0
(2s − 1) = 0 or (s − √2) = 0
s = 1/2 or s = √2
Thus, the zeros of h (s) = (2s - 1)(s - √2) are α = 1/2 and β = √2
Now,
Sum of the zeros = α+β
= 1/2 + √2
and
(-Coefficient of s/Coefficient of s2)
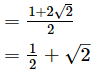
Therefore, sum of the zeros = (-Coefficient of x/Coefficient of x2)
Product of the zeros = αβ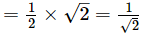
and
Constant term/Coefficient of s2
Therefore,
Product of the zeros = Constant term/Coefficient of x2
Hence, the relation-ship between the zeros and coefficient are verified.
(x) f(v) = v2 + 4√3v −15
f(v) = v2 + 5√3v − √3v − 15
= v2 − √3v + 5√3v − 15
= v(v − √3) + 5√3 (v − √3)
= (v - √3)(v + 5√3)
The zeros of f(v) are given by
f(v) = 0
v2 + 4√3v − 15 = 0
(v + 5√3)(v − √3) = 0
(v − √3) = 0 or (v + 5√3) = 0
v = √3 or v = −5√3
Thus, the zeros of f(v) = (v − √3)(v + 5√3) are α = √3 and β = −5√3.
Now,
Sum of the zeros = α + β
= √3 −5√3= −4√3
and
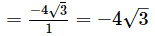
Therefore, sum of the zeros = (-Coefficient of x/Coefficient of x2)
Product of the zeros = αβ
=√3 × (−5√3) = −15
and
Constant term / Coefficient of v2
= -15/1 = -15
Therefore,
Product of the zeros = Constant term/Coefficient of s2
Hence, the relationship between the zeros and coefficient are verified.
(xi) h(s) = 2s2 − (1 + 2√ 2)s + √2
h(s) = 2s2 − s − 2√2s + √2
h(s) =s (2s − 1) − √2(2s − 1)
h(s) = (2s −1)(s − √2)
The zeros of h(s) are given by
h(s) = 0
2s2 − (1 + 2√2)s +√2 = 0
(2s − 1)(s − √2) = 0
(2s − 1) = 0 or (s − √2) = 0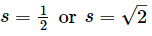
Thus, the zeros of h(s) = (2s − 1)(s − √2) are α = 1/2 and β = √2
Now,
Sum of the zeros = α + β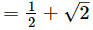
and
−Coefficient of s/Coefficient of s2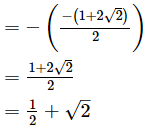
Therefore, sum of the zeros = −Coefficient of x/Coefficient of x2
Product of the zeros = αβ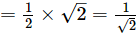
and
Constant term/Coefficient of s2
Therefore,
Product of the zeros = Constant term/Coefficient of s2
Hence, the relationship between the zeros and coefficient are verified.
(x) f(v) = v2 + 4√3v − 15
f(v) = v2 + 5√3v − √3v − 15
= v2 − √3v + 5√3v − 15
= v(v − √3) + 5√3 (v − √3)
= (v − √3)(v + 5√3)
The zeros of f(v) are given by
f(v) = 0
v2 + 4√3v − 15 = 0
(v + 5√3)(v − √3) = 0
(v − √3) = 0 or (v + 5√3) = 0
v = √3 or v = −5√3
Thus, the zeros of f(v) = (v − √3)(v + 5√3) are α = √3 and β = −5√3.
Now,
Sum of the zeros = α + β
=√3 − 5√3 = −4√3
and
−Coefficient of v/Coefficient of v2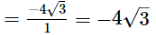
Therefore, sum of the zeros = −Coefficient of x/Coefficient of x2
Product of the zeros = αβ
= √3 × (−5√3) = −15
and
Constant term/Coefficient of v2
= -15/1 = −15
Therefore,
Product of the zeros = Constant term/Coefficient of x2
Hence, the relation-ship between the zeros and coefficient are verified.
(xi) 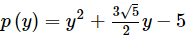
p(y) 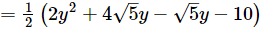
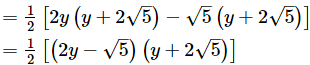
The zeros are given by p(y) = 0.
Thus, the zeros of p(y)= 1/2 (2y − √5)(y + 2√5) are α 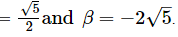
Now,
Sum of the zeros = α + β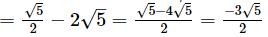
and
−Coefficient of y/Coefficient of y2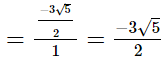
Therefore, sum of the zeros = −Coefficient of x/Coefficient of x2
Product of the zeros = αβ
= −5
and
Constant term/Coefficient of y2
= -5/1 = -5
Therefore,
Product of the zeros = Constant term/Coefficient of x2
Hence, the relationship between the zeros and coefficient are verified.
(xii) 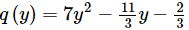

= 1/3 (21y2 − 14y + 3y − 2)
= 1/3 [7y(3y − 2) + 1 (3y − 2)]
= 1/3 [(7y + 1)(3y − 2)]
The zeros are given by q(y) = 0.
Thus, the zeros of q(y) = 1/3 (7y + 1)(3y − 2) are α = -1/7 and β = 2/3.
Now,
Sum of the zeros = α + β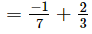
= 11/21
and
−Coefficient of y/Coefficient of y2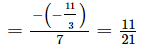
Therefore, sum of the zeros = −Coefficient of x/Coefficient of x2
Product of the zeros = αβ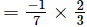
= -2/21
and
Constant term/Coefficient of y2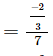
= -2/21
Therefore,
Product of the zeros = Constant term/Coefficient of x2
Hence, the relationship between the zeros and coefficient are verified.
FAQs on Chapter 2 - Polynomials, RD Sharma Solutions - (Part-1) - RD Sharma Solutions for Class 10 Mathematics
| 1. What are polynomials? |  |
| 2. How do you classify polynomials based on the number of terms they have? |  |
| 3. What is the degree of a polynomial and how is it determined? |  |
| 4. How can polynomials be added and subtracted? |  |
| 5. How can polynomials be multiplied and divided? |  |


















