Chapter 2 - Polynomials, RD Sharma Solutions - (Part-2) | RD Sharma Solutions for Class 10 Mathematics PDF Download
Page No 2.34
Ques.2. For each of the following, find a quadratic polynomial whose sum and product respectively of the zeroes are as given. Also, find the zeroes of these polynomials by factorization.
(i) -(8/3), (4/3)
(ii) (21/8), (5/16)
(iii) -2√3, -9
(iv) 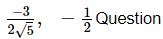
Ans. We know that a quadratic polynomial whose sum and product of zeroes are given is
f(x) = k{x2−(Sum of zeroes)x + Product of zeroes}
(i) We have, sum of zeroes = -8/3 and product of zeroes = 4/3
So, the required quadratic polynomial will be 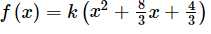
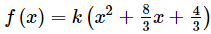
= k/3(3x2 + 8x + 4)
= k/3((3x2 + 6x + 2x + 4)
= k/3 (3x(x + 2) + 2(x + 2))
= k/3 (3x + 2)(x + 2)
Now, the zeroes are given by f(x) = 0.
Thus, x = -(2/3) and x = −2
(ii) We have, sum of zeroes = 21/8 and product of zeroes = 5/16
So, the required quadratic polynomial will be f(x) = k 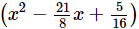
f(x) = k 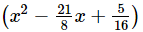
= k/16 (16x2 − 42x + 5)
= k/16 (16x2 − 40x − 2x + 5)
= k/16 (16x2 − 2x − 40x + 5)
= k/3 (2x(8x − 1) −5 (8x − 1)
= k/3 (8x − 1)(2x − 5)
Now, the zeroes are given by f(x) = 0.
Thus, x = 1/8 and x = 5/2
(iii) We have, sum of zeroes = −2√3 and product of zeroes = −9.
So, the required quadratic polynomial will be f(x) = k(x2 + 2√3x − 9).
f(x) = k(x2 + 2√3x − 9)
= k(x2 + 3√3x − √3x − 9)
= k(x + 3√3)(x − √3)
Now, the zeroes are given by f(x) = 0.
Thus, x = −3√3 and x = √3.
(iv) We have, sum of zeroes = 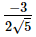 and product of zeroes = -1/2
and product of zeroes = -1/2
So, the required quadratic polynomial will be f(x) = 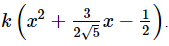
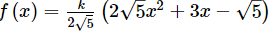
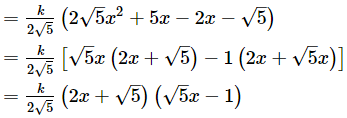
Now, the zeroes are given by f(x) = 0.
Thus, x = 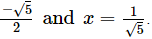
Ques.3. If α and β are the zeros of the quadratic polynomial f(x) = x2 − 5x + 4, find the value of 
Ans. Since α and β are the zeros of the quadratic polynomial f(x) = x2 - 5x + 4
Therefore α + β = -Coefficient of x/Coefficient of x2
= (-5)/1
= 5
αβ = Constant term/Coefficient of x2
= 4/1
= 4
We have, (1/α)+(1/β) - 2αβ
(1/α)+(1/β) - 2αβ = (1/α)+(1/β) - 2αβ
(1/α)+(1/β) - 2αβ = 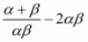
By substituting α + β = 5 and αβ = 4 we get,
(1/α)+(1/β) - 2αβ = (5/4) - 2(4)
(1/α)+(1/β) - 2αβ = 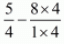
Taking least common factor we get,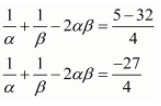
Hence, the value of (1/α)+(1/β) - 2αβ is 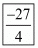 .
.
Ques.4. If α and β are the zeros of the quadratic polynomial p(y) = 5y2 − 7y + 1, find the value of (1/α)+(1/β).
Ans. Since α and β are the zeros of the quadratic polynomial p(y) = 5y2 - 7y + 1
α + β = -Coefficient of x/Coefficient of x2
= -((-7)/5)
= 7/5
αβ = Constant term/Coefficient of x2
= 1/5
We have, 
By substituting α + β = 7/5 and αβ = 1/5 we get,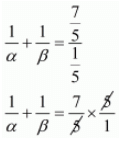
1/α + 1/β = 7
Hence, the value of 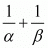 is
is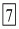 .
.
Ques.5. If α and β are the zeros of the quadratic polynomial f(x) = x2 − x − 4, find the value of ((1/α) + (1/β) - (αβ)).
Ans. Since α and β are the zeros of the quadratic polynomials f(x) = x2 + x - 2
Sum of the zeros = -Coefficient of x/Coefficient of x2
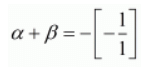
α + β = 1/1
α + β = 1
Product if zeros = Constant term/Coefficient of x2
αβ = (-4)/1
αβ = -4
We have,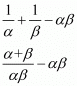
By substituting α + β =1 and αβ = -4 we get,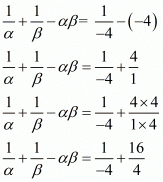
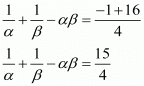
Hence, the value of is
is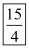 .
.
Ques.6. If α and β are the zeros of the quadratic polynomial f(x) = x2 + x − 2, find the value of 1/α - 1/β.
Ans. Since α and β are the zeros of the quadratic polynomials f(x) = x2 + x - 2
Sum of the zeros = -Coefficient of x/Coefficient of x2
α + β = -(1/1]
α + β = -1
Product if zeros = Constant term/Coefficient of x2
αβ = (-2)/1
αβ = -2
We have, 1/α - 1/β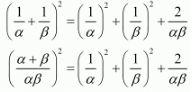
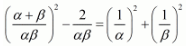
By substituting α + β = -1 and αβ = -2 we get,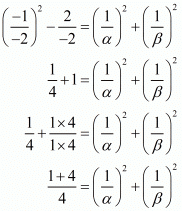
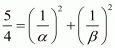
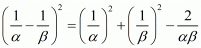
By substituting 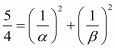 in
in 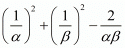 we get ,
we get , 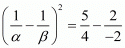
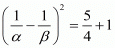

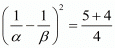
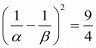
Taking square root on both sides we get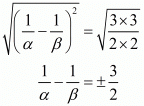
Hence, the value of 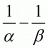 is
is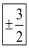 .
.
Ques.7. If one zero of the quadratic polynomial f(x) = 4x2 − 8kx − 9 is negative of the other, find the value of k.
Ans. Since α and -α are the zeros of the quadratic polynomial
α - α = 0
-Coefficient of x/Coefficient of x2 = 0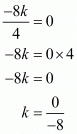
k = 0
Hence, the Value of k is 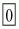 .
.
Ques.8. If the sum of the zeros of the quadratic polynomial f(t) = kt2 + 2t + 3k is equal to their product, find the value of k.
Ans. Let α, β be the zeros of the polynomial f(t) = kt2 + 2t + 3k.Then,
α + β = -Coefficient of x/Coefficient of x2
α + β = -2/k
αβ = Constant term/Coefficient of x2
αβ = 3k/k
αβ = 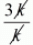
αβ = 3
It is given that the sum of the zero of the quadratic polynomial is equal to their product then, we have
α + β = αβ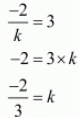
Hence, the value of k is 
Ques.9. If α and β are the zeros of the quadratic polynomial p(x) = 4x2 − 5x − 1, find the value of α2β + αβ2.
Ans. Since α and β are the zeros of the quadratic polynomials p(x) = 4x2 − 5x − 1
Sum of the zeros = -Coefficient of x/Coefficient of x2 
Product of zeros = Constant term/Coefficient of x2
αβ = -(1/4)
We have, α2β + αβ2
α2β + αβ2 = αβ(α + β)
By substituting  and
and  in
in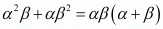 , we get
, we get 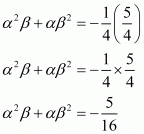
Hence, the value of α2β + αβ2 is .
.
Ques.10. If α and β are the zeros of the quadratic polynomial f(t) = t2 − 4t + 3, find the value of α4β3 + α3β4.
Ans. Since α and β are the zeros of the quadratic polynomials p(y) = t2 − 4t + 3
α + β = -Coefficient of x/Coefficient of x2 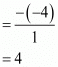
αβ = Constant term/Coefficient of x2
= 3/1
= 3
We have α4β3 + α3β4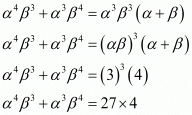
α4β3 + α3β4 = 108
Hence, the value of α4β3 + α3β4 is .
.
Ques.11. If α and β are the zeros of the quadratic polynomial f(x) = 6x2 + x − 2, find the value of α/β + β/α.
Ans. Since α and β are the zeros of the quadratics polynomial
f (x) = 6x2 + x - 2
sum of zeros = -Coefficient of x/Coefficient of x2
α + β = -(1/6)
Product of the zeros = Constant term/Coefficient of x2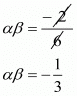
We have, 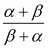
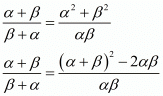
By substituting α + β = -1/6 and αβ = -(1/3) we get,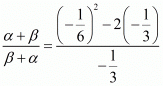
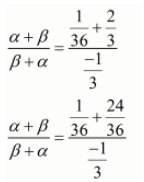
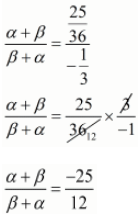
Hence, the value of 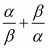 is
is 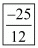 .
.
Ques.12. If α and β are the zeros of the quadratic polynomial p(s) = 3s2 − 6s + 4, find the value of 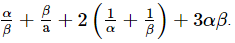
Ans. Since α and β are the zeros of the quadratic polynomial p(s) = 3s2 - 6s + 4
α + β = -Coefficient of x/Coefficient of x2 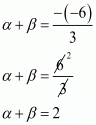
αβ = Constant term/Coefficient of x2
αβ = 4/3
We have, 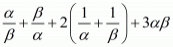
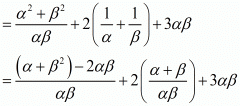
By substituting α + β = 2 and αβ = 4/3 we get,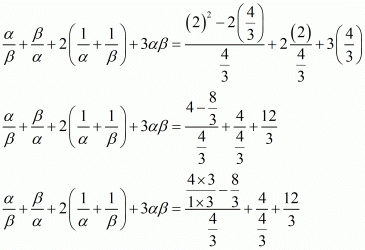
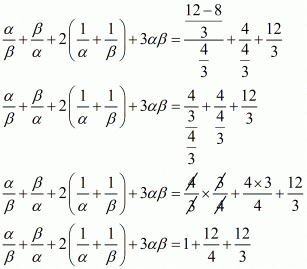
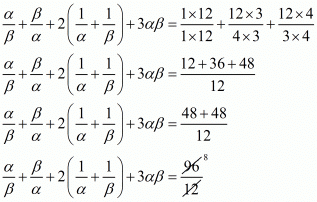
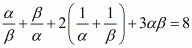
Hence, the value of 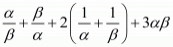 is
is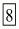
Page No 2.35
Ques.13. If the squared difference of the zeros of the quadratic polynomial f(x) = x2 + px + 45 is equal to 144, find the value of p.
Ans. Given α and β are the zeros of the quadratic polynomial f(x) = x2 + px + 45
α + β = -Coefficient of x/Coefficient of x2
= (-p)/1
= -p
αβ = Constant term/Coefficient of x2
= 45/1
= 45
We have,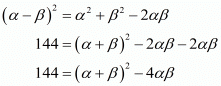
Substituting α + β = -p and αβ = 45 then we get,
144 = (-p)2 - 4 x 4
144 = p2 - 4 x 45
144 = p2 - 180
144 + 180 = p2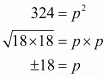
Hence, the value of p is 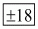 .
.
Ques.14. If α and β are the zeros of the quadratic polynomial f(x) = x2 − px + q, prove that 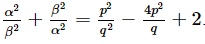
Ans. Since α and β are the zeros of the quadratic polynomial f(x) = x2 - px + q
α + β = -Coefficient of x/Coefficient of x2 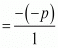
= p
αβ = Constant term/Coefficient of x2
= q/1
= q
We have,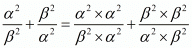
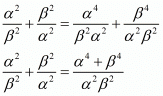


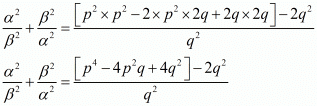
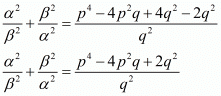
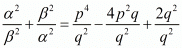
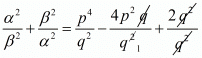
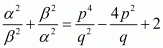
Hence, it is proved that 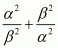 is equal to
is equal to 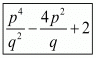 .
.
Ques.15. If α and β are the zeros of the quadratic polynomial f(x) = x2 − p(x + 1) − c, show that (α + 1) (β + 1) = 1 − c.
Ans. Since α and β are the zeros of the quadratic polynomial f(x) = x2 - p(x + 1) - c
Then
x2 - p(x + 1) - c
x2 - px - p - c
α + β = -Coefficient of x/Coefficient of x2 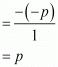
αβ = Constant term/Coefficient of x2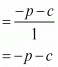
We have to prove that (α + 1)(β + 1)= 1 - c
(α + 1)(β + 1) = 1 - c
(α + 1)β+(α + 1)(1) = 1 - c
αβ + β + α + 1 = 1 - c
αβ + (α + β) + 1 = 1 - c
Substituting (α + β) = p and αβ = -p-c we get, 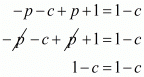
Hence, it is shown that (α + 1)(β + 1) = 1 - c.
Ques.16. If α and β are the zeros of a quadratic polynomial such that α + β = 24 and α − β = 8, find a quadratic polynomial have α and β as its zeros.
Ans. Given
α + β = 24 ....(i)
α - β = 8 ....(ii)
By subtracting equation (ii) from (i) we get 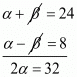
α = 32/2
α = 16
Substituting α = 16in equation (i) we get,
α + β = 24
16 + β = 24
β = 24 - 16
β = 8
Let S and P denote respectively the sum and product of zeros of the required polynomial. then,
S = α + β
16 + 8
= 24
P = αβ
= 16 x 8
= 128
Hence, the required polynomial if f(x) is given by
f(x) = k(x2 - Sx + P)
f(x) = k(x2 - 24x + 128)
Hence, required equation is f(x) = k(x2 - 24x + 128) where k is any non-zeros real number.
Ques.17. If α and β are the zeros of the quadratic polynomial f(x) = x2 − 1, find the quadratic polynomial whose zeros are 2α/β and 2β/α.
Ans. Since α and β are the zeros of the quadratic polynomial f(x) = x2 - 1
The roots are α and β
α + β = -Coefficient of x/Coefficient of x2
α + β = 0/1
α + β = 0
αβ = Constant term/Coefficient of x2
αβ = -1/1
αβ = -1
Let S and P denote respectively the sum and product of zeros of the required polynomial. Then,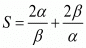
Taking least common factor we get,
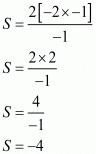
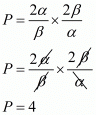
Hence, the required polynomial f(x) is given by,
f(x) = k(x2 - Sx + p)
f(x) = k(x2 -(-4)x + 4)
f(x) = k(x2 + 4x + 4)
Hence, required equation is f(x) = k(x2 + 4x + 4) Where k is any non zero real number.
Ques.18. If α and β are the zeros of the quadratic polynomial f(x) = x2 − 3x − 2, find a quadratic polynomial whose zeros are 1/(2α + β) and 1/(2β + α).
Ans. Since α and β are the zeros of the quadratic polynomial f(x) = x2 - 3x - 2
The roots are α and β
α + β = -Coefficient of x/Coefficient of x2
α + β = -((-3)/(1))
α + β = -(-3)
α + β = 3
αβ = Constant term/Coefficient of x2
αβ = (-2)/1
αβ = -2
Let S and P denote respectively the sum and the product of zero of the required polynomial . Then,
Taking least common factor then we have ,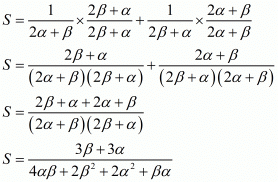

By substituting α + β = 3 and αβ = -2 we get,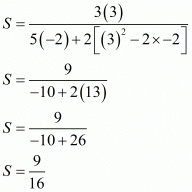
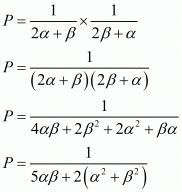
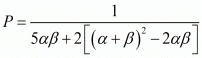
By substituting α + β = 3 and αβ = -2 we get ,
P = 1/16
Hence, the required polynomial f(x) is given by
Hence, the required equation is 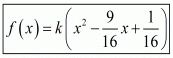 Where k is any non zero real number.
Where k is any non zero real number.
Ques.19. If α and β are the zeros of the polynomial f(x) = x2 + px + q, from a polynomial whose zeros are (α + β)2 and (α − β)2.
Ans. If α and β are the zeros of the quadratic polynomial f(x) = x2 + px + q
α + β = -Coefficient of x/Coefficient of x2
= (-p)/1
αβ = Constant term/Coefficient of x2
= q/1
= q
Let S and P denote respectively the sums and product of the zeros of the polynomial whose zeros are (α + β)2 and (α - β)2. Then,
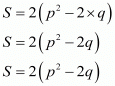
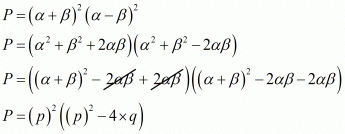
P = p2 (p2 - 4q)
The required polynomial of f(x) = k(kx2 - sx + p)is given by 
 , where k is any non-zero real number.
, where k is any non-zero real number.
Ques.20. If α and β are the zeros of the quadratic polynomial f(x) = x2 − 2x + 3, find a polynomial whose roots are (i) α + 2, β + 2 (ii)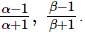
Ans. (i) Since α and β are the zeros of the quadratic polynomial f(x) = x2 - 2x + 3
α + β = -Coefficient of x/Coefficient of x2
= -((-2))/1
= 2
Product of the zeros = Constant term/Coefficient of x2
= 3/1
= 3
Let S and P denote respectively the sums and product of the polynomial whose zeros α + 2, β + 2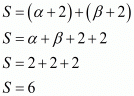

P = 3 + 4 + 4
P = 11
Therefore the required polynomial f (x) is given by
f(x) = k(x2 - Sx + P)
= k(x2 - 6x + 11)
Hence, the required equation is f(x) = k(x2 - 6x + 11).
(ii) Since α and β are the zeros of the quadratic polynomial f(x) = x2 - 2x + 3
α + β = -Coefficient of x/Coefficient of x2
= -((-2))/1
= 2
Product of the zeros = Constant term/Coefficient of x2
= 3/1
= 3
Let S and P denote respectively the sums and product of the polynomial whose zeros 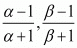
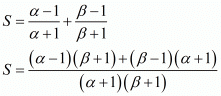
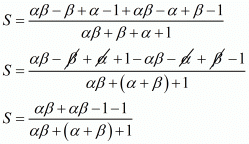
By substituting α + β = 2 and αβ = 3 we get,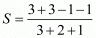
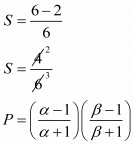
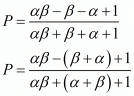
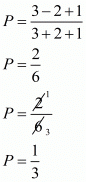
The required polynomial f (x) is given by,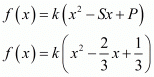
Hence, the required equation is 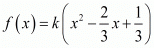 , where k is any non zero real number.
, where k is any non zero real number.
FAQs on Chapter 2 - Polynomials, RD Sharma Solutions - (Part-2) - RD Sharma Solutions for Class 10 Mathematics
| 1. What are the different types of polynomials? |  |
| 2. How can we determine the degree of a polynomial? |  |
| 3. What is the role of coefficients in polynomials? |  |
| 4. How can we add or subtract polynomials? |  |
| 5. Can polynomials have negative exponents? |  |

|
Explore Courses for Class 10 exam
|

|
















