Chapter 2 - Polynomials, RD Sharma Solutions - (Part-3) | RD Sharma Solutions for Class 10 Mathematics PDF Download
Page No 2.35
Ques.21. If α and β are the zeroes of the quadratic polynomial f(x) = ax2 + bx + c, then evaluate :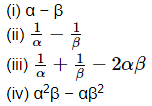
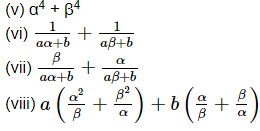
Ans. (i) Given α and β are the zeros of the quadratic polynomial f(x) = ax2 + bx + c
α + β = -Coefficient of x/Coefficient of x2
= -b/a
αβ = Constant term/Coefficient of x2
= c/a
We have, (α - β)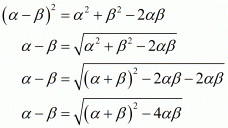
Substituting α + β = (-b)/a and αβ = c/a then we get, 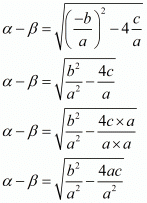

Hence, the value of α - β is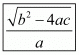 .
.
(ii) Given α and β are the zeros of the quadratic polynomial f(x) = ax2 + bx + c
α + β = -Coefficient of x/Coefficient of x2
= (-b)/a
αβ = Constant term/Coefficient of x2
= c/a
We have,
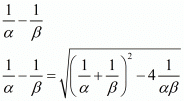
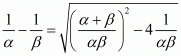
Substituting α + β = (-b)/a and αβ = c/a then we get,
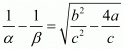
By taking least common factor we get,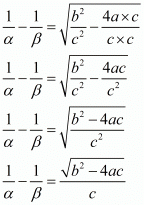
Hence the value of  is
is  .
.
(iii) Given α and β are the zeros of the quadratic polynomial f(x) = ax2 + bx + c
α + β = -Coefficient of x/Coefficient of x2
= (-b)/a
αβ = Constant term/Coefficient of x2
= c/a
We have, 
By cross multiplication we get,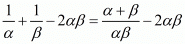
By substituting α + β = -b/a and αβ = c/a we get,
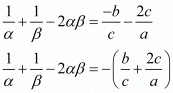
Hence the value of 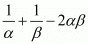 is
is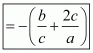 .
.
(iv) Given α and β are the zeros of the quadratic polynomial f(x) = ax2 + bx + c
α + β = -Coefficient of x/Coefficient of x2
= (-b)/a
αβ = Constant term/Coefficient of x2
= c/a
We have, α2β + αβ2
By taking common factor αβ we get, = 2β(α + β)
By substituting α + β = -b/a and αβ = c/a we get, 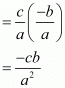
Hence the value of α2β + αβ2 is (-cb)/a2.
(v) Given α and β are the zeros of the quadratic polynomial f(x) = ax2 + bx + c
α + β = -Coefficient of x/Coefficient of x2
= (-b)/a
αβ = Constant term/Coefficient of x2
= c/a
We have,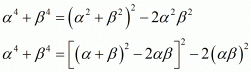
By substituting α + β = -b/a and αβ = c/a we get,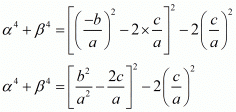
By taking least common factor we get
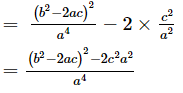
Hence the value of α4 + β4 is 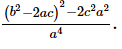
(vi) Since α and β are the zeros of the quadratic polynomial f(x) = ax2 + bx + c
α + β = -Coefficient of x/Coefficient of x2
= (-b)/a
αβ = Constant term/Coefficient of x2
= c/a
We have,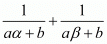
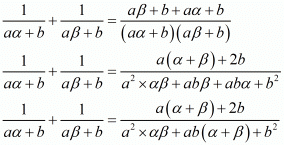
By substituting α + β = -b/a and αβ = c/a we get,
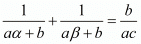
Hence, the value of 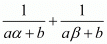 is
is  .
.
(vii) Since α and β are the zeros of the quadratic polynomial f(x) = ax2 + bx + c
α + β = -Coefficient of x/Coefficient of x2
= (-b)/a
αβ = Constant term/Coefficient of x2
= c/a
We have, 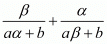
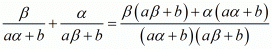
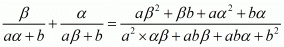
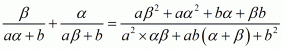
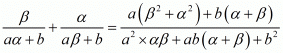
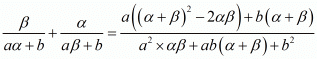
By substituting α + β = -b/a and αβ = c/a we get,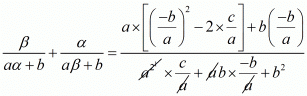
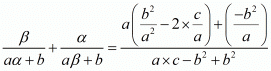

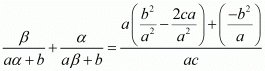
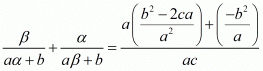
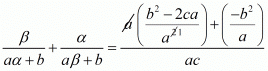
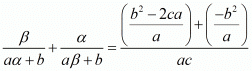

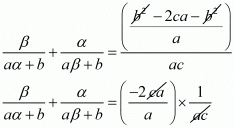
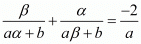
Hence, the value of 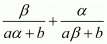 is
is  .
.
(viii) Since α and β are the zeros of the quadratic polynomial f(x) = ax2 + bx + c
α + β = -Coefficient of x/Coefficient of x2
= (-b)/a
αβ = Constant term/Coefficient of x2
= c/a
We have,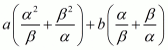
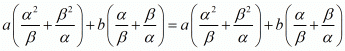
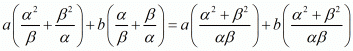
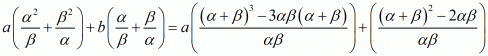
By substituting α + β = -b/a and αβ = c/a we get,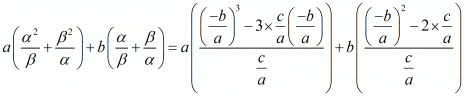
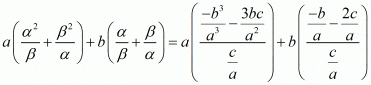
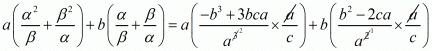
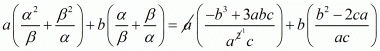
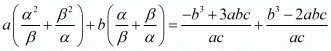
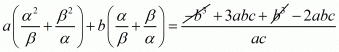

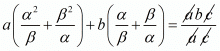
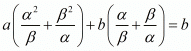
Hence, the value of 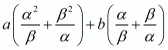 is
is  .
.
Page No 2.43
Ques.1. Verify that the numbers given along side of the cubic polynomials below are their zeros. Also, verify the relationship between the zeros and coefficients in each case:
(i) f(x) = 2x3+x2 − 5x + 2; 1/2, 1, −2
(ii) g(x) = x3 − 4x2 + 5x − 2; 2, 1, 1
Ans. (i) We have,
f(x) = 2x3 + 2x2 − 5x + 2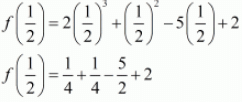
f(1/2) = 0
f(1) = 2(1)3 + (1)2 - 5(1) + 2
f(1) = 2 + 1 - 5 + 2
f(1) = 0
f(-2) = 2(-2)3 + (-2)2 - 5(-2) + 2
f(-2) = -16 + 4 + 10 + 2
f(-2) = 0
So, 1/2, 1 and 2 are the zeros of polynomial p(x)
Let α = 1/2, β = 1 and γ = -2. Then
α + β + γ = 1/2 + 1 - 2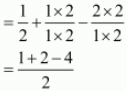
= (-1)/2
From f(x) = 2x3 + 2x2 - 5x + 2
α + β + γ = (-Coefficient of x2)/Coefficient of x3
α + β + γ = -(1/2)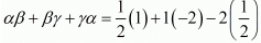
= 1/2 - 2 - 2/2
Taking least common factor we get,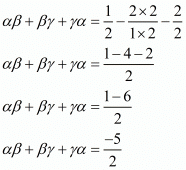
From f(x) = 2x3 + 2x2 - 5x + 2
αβ + βγ + γα = Coefficient of x/Coefficient of x3
αβ + βγ + γα = (-5)/2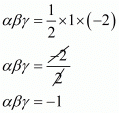
From f(x) = 2x3 + 2x2 - 5x + 2
αβγ = (-Constant term)/Coefficient of x2
αβγ = 
αβγ = -1
Hence, it is verified that the numbers given along side of the cubic polynomials are their zeros and also verified the relationship between the zeros and coefficients
(ii) We have,
g(x) = x3 - 4x2 + 5x - 2
g(2) = (2)3 - 4(2)2 + 5(2) - 2
g(2) = 8 - 16 + 10 - 2
g(2) = 0
g(1) = (1)3 - 4(1)2 + 5(1) - 2
= 1 - 4 + 5 - 2
= 0
g(1) = (1)3 - 4(1)2 + 5(1) - 2
= 1 - 4 + 5 - 2
= 0
So 2, 1 and 1 are the zeros of the polynomial g(x)
Let α = 2, β = 1 and λ = 1. Then,
α + β + γ = 2 + 1 + 1
α + β + γ = 4
From g(x) = x3 - 4x2 + 5x - 2
α + β + γ = Coefficient of x2/Coefficient of x3
α + β + γ = 4/1
α + β + γ = 4
αβ + βγ + γα = 2(1) + 1(1) + 1(2)
αβ + βγ + γα = 2 + 1 + 2
αβ + βγ + γα = 5
From g(x) = x3 - 4x2 + 5x - 2
αβ + βγ + γα = Coefficient of x/Coefficient of x3
αβ + βγ + γα = 5/1
αβ + βγ + γα = 5
αβγ = 2 x 1 x 1
αβγ = 2
From g(x) = x3 - 4x2 + 5x - 2
αβγ = (-Constant term)/Coefficient of x2
αβγ = -((-2)/1)
αβγ = 2
Hence, it is verified that the numbers given along side of the cubic polynomials are their zeros and also verified the relationship between the zeros and coefficients.
Ques.2. Find the cubic polynomial with the sum, sum of the product of its zeros taken two at a time, and product of its zeros as 3, −1 and − 3 respectively.
Ans. If α, β and γ are the zeros of a cubic polynomial f(x), then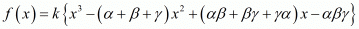 where k is any non-zero real number.
where k is any non-zero real number.
Here,
α + β + γ = 3,
αβ + βγ + γα = -1
αβγ = -3
Therefore
f(x) = k{x3 - (3)x2 + (-1)x - (-3)}
f(x) = k{x3 - 3x2 - 1x + 3}
Hence, cubic polynomial is f(x) = k{x3 - 3x2 - 1x + 3}, where k is any non-zero real number.
Ques.3. If the zeros of the polynomial f(x) = 2x3 − 15x2 + 37x − 30 are in A.P., find them.
Ans. Let α = a - d, β = a and γ = a + d be the zeros of the polynomial
f(x) = 2x3 - 15x2 + 37x - 30
Therefore
α + β + γ = Coefficient of x2/Coefficient of x3
= -((-15)/2)
= 15/2
αβγ = (-Constant term)/Coefficient of x2
= -((-30)/2)
= 15
Sum of the zeros = Coefficient of x2/Coefficient of x3

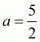
Product of the zeros = (-Constant term)/Coefficient of x2
αβγ = 15
(a - d) + a + (a + d) = 15
a(a2 - d2) = 15
Substituting a = 5/2 we get
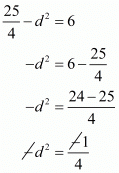
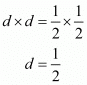
Therefore, substituting a = 5/2 and d = 1/2 in α = a - d, β = a and γ = a + d
α = a - d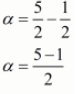
α = 4/2
α = 2
β = a
β = 5/2
γ = a + d
γ = 6/2
γ = 3
Hence, the zeros of the polynomial are 2, 5/2, 3.
Ques.4. Find the condition that the zeros of the polynomial f(x) = x3 + 3px2 + 3qx + r may be in A.P.
Ans. Let a-d, a and a+ d be the zeros of the polynomials f(x).Then,
Sum of the zeros = Coefficient of x2/Coefficient of x3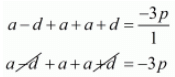
3a = -3p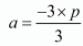
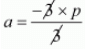
a = -p
Since a is a zero of the polynomial f(x). Therefore, 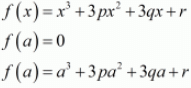
a3 + 3pa2 + 3qa + r = 0
Substituting a = -p we get,
(-p)3 + 3p(-p)2 + 3q(-p) + r = 0
-p3 + 3p3 - 3pq + r = 0
2p3 - 3pq + r = 0
Hence, the condition for the given polynomial is 2p3 - 3pq + r = 0.
Ques.5. If the zeros of the polynomial f(x) = ax3 + 3bx2 + 3cx + d are in A.P., prove that 2b3 − 3abc + a2d = 0.
Ans. Let a - d, a and a + d be the zeros of the polynomial f(x). Then,
Sum of the zeros = Coefficient of x2/Coefficient of x3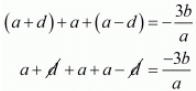
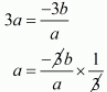
a = (-b)/a
Since a is a zero of the polynomial f(x).
Therefore,
f(x) = ax3 + 3bx2 + 3cx + d
f(a) = 0
f(a) = aa3 + 3ba2 + 3ca + d
aa3 + 3ba2 + 3ca + d = 0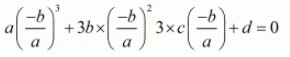
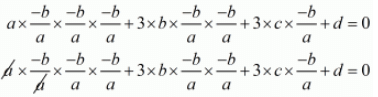

2b3 + 3abc +a2d = 0 x a2
2b3 - 3abc + a2d = 0
Hence, it is proved that 2b3 - 3abc + a2d = 0.
Ques.6. If the zeros of the polynomial f(x) = x3 − 12x2 + 39x + k are in A.P., find the value of k.
Ans. Let a - d, a and a + d be the zeros of the polynomial f(x).
Then,
Sum of the zeros = Coefficient of x2/Coefficient of x3
3a = 12
a = 12/3
a = 4
Since a is a zero of the polynomial f(x)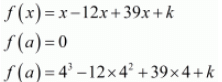

-28 = k
Hence, the value of k is -28.
FAQs on Chapter 2 - Polynomials, RD Sharma Solutions - (Part-3) - RD Sharma Solutions for Class 10 Mathematics
| 1. What are polynomials? |  |
| 2. What is the degree of a polynomial? |  |
| 3. How do you add and subtract polynomials? |  |
| 4. How do you multiply polynomials? |  |
| 5. What is the remainder theorem? |  |

|
Explore Courses for Class 10 exam
|

|

















