Chapter 4 - Quadratic Equations, RD Sharma Solutions - (Part-1) - Class 10 PDF Download
Page No 4.19
Q.1. Solve the following quadratic equations by factorization:
(x − 4) (x + 2) = 0
Ans.
We have been given,
(x- 4)(x - 2) = 0
Therefore,
(x - 4) = 0
x = 4
or,
(x+2) = 0
x = -2
Therefore,
x = 4 or x = -2
Q.2. Solve the following quadratic equations by factorization:
(2x + 3)(3x − 7) = 0
Ans.
We have been given,
(2x + 3)(3x-7) = 0
Therefore,
(2x+ 3) = 0
2x =-3
x = -3/2
or,
(3x-7) = 0
3x = 7
x = 7/3
Therefore,
x = -3/2 or x = 7/3
Q.3. Solve the following quadratic equations by factorization: 3x − 14x − 5 = 0
Ans.
We have been given
3x2 - 14x - 5 = 0
3x2 - 15x + x - 5 = 0
3x(x - 5) +1(x - 5) = 0
(3x + 1)(x - 5) = 0
Therefore,
3x+1 = 0
3x = -1
x = -1/3
or,
x-5 = 0
x = 5
Hence, x = -1/3 or x = 5
Q.4. Solve the following quadratic equations by factorization:
9x2 − 3x − 2 = 0
Ans.
We have been given,
9x2 - 3x - 2 = 0
9x2 - 6x + 3x - 2 = 0
3x(3x-2)+1(3x-2) = 0
(3x+1)(3x-2) = 0
Therefore,
3x+1 = 0
3x = -1
x = -1/3
or,
3x-2 = 0
3x = 2
Hence,
x = -1/3 or x = 2/3
Q.5. Solve the following quadratic equations by factorization: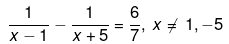
Ans.
We have been given 
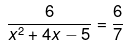
x2 + 4x-12 = 0
x2+6x - 2x - 12 = 0
x(x+6)-2(x+6) = 0
(x-2)(x+6) = 0
Therefore,
x-2 = 0
x= 2
or,
x+6 = 0
x = -6
Hence,
x=2 or x = -6
Q.6. Solve the following quadratic equations by factorization:
6x2 + 11x + 3 = 0
ANS.
We have been given
6x2+11x+3 = 0
6x2+9x-2x +3 = 0
3x(2x+3)+1(2x+3) = 0
(2x+3)(3x+1) = 0
2x+3 = 0
x = -3/2
or,
3x+1 = 0
x = -1/3
Hence,
x = -3/2 or x = -1/3
Q.7. Solve the following quadratic equations by factorization:
5x2 − 3x − 2 = 0
Ans.
We have been given
5x2 − 3x − 2 = 0
5x2-5x+2x-2 = 0
5x(x-1)+2(x-1) = 0
(5x+2)(x-1) = 0
Therefore,
5x+2 = 0
5x = -2
x = -2/5
or,
x - 1 = 0
x = 1
Hence,
x = -2/5 or x = 1
Q.8. Solve the following quadratic equations by factorization:
48x2 − 13x − 1 = 0
ANS.
We have been given
48x2 − 13x − 1 = 0
48x2 - 16x + 3x - 1 = 0
16x(3x-1)+1(3x-1) = 0
(16x+1)(3x-1) = 0
Therefore,
16x+1 = 0
16x = -1
x = -1/16
or
3x-1 = 0
3x = 1
x = 1/3
Hence,
x = -1/16 or x = 1/3
Q.9. Solve the following quadratic equations by factorization:
3x2 = −11x − 10
ANS.
We have been given
3x2 = −11x − 10
3x2 + 11x + 10 = 0
3x2+6x+5x +10 = 0
3x(x+2)+5 (x+2)=0
(3x+5)(x+2)=0
Therefore,
3x+5 = 0
3x = -5
x = -5/3
or,
x+2 =0
x = -2
Hence,
x = -5/3 or x = -2
Q.10. Solve the following quadratic equations by factorization:
25x (x + 1) = −4
ANS.
We have been given
25x (x + 1) = −4
25x2+25x+4 = 0
25x2+20x + 5x + 4 = 0
5x(5x+4)+1(5x+4) = 0
(5x+1)(5x+4) = 0
Therefore,
5x+1 = 0
5x = -1
x = -1/5
or,
5x+4 = 0
5x = -4
x = -4/5
Hence,
x = -1/5 or x = -4/5
Q.11. Solve the following quadratic equations by factorization: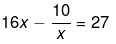
Ans.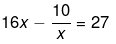
16x2 - 10 = 27x
16x2 - 27x - 10 = 0
16x2 -32x + 5x - 10 = 0
16x(x-2) + 5(x - 2) = 0
(16x+5)(x-2) = 0
16x + 5 = 0 or x = 2 = 0
x = -5/16 or x = 2
Hence, the factor are 2 and -5/16
Q.12. Solve the following quadratic equations by factorization: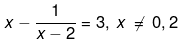
Ans.
We have been given
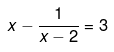
-2x = 3x2 - 6x
3x2 - 6x + 2 = 0
3x2 - (3 + √3)x-(3-√3)x+3-√3+√3-1=0
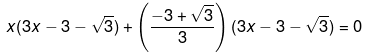
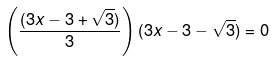
(√3x - √3+1)(√3x - √3-1)=0
Therefore,
√3x - √3+1=0
√3x = √3-1
x = (√3-1)/√3
or,
√3x - √3-1
√3x = √3+1
x = (√3+1)/√3
Hence,
x = (√3-1)/√3 or x = (√3+1)/√3
Q.13. Solve the following quadratic equations by factorization: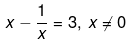
Ans.
We have been given
x - 1/x = 3
x2-1 = 3x
x2 - 3x -1 = 0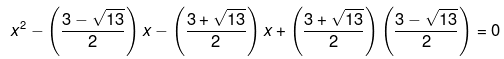

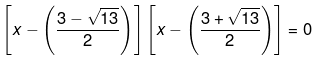
Therefore,
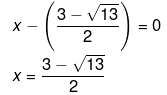
or,
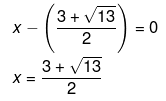
Hence
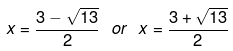
Q.14. Solve the following quadratic equations by factorization: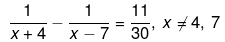
Ans.
We have been given
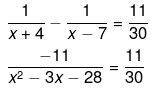
-30x = x2 - 3x - 28
-3x + 2 = 0
x2 - 2x - x + 2 = 0
x(x-2)-1(x-2) = 0
(x-1)(x-2) = 0
Therefore,
x-1=0
x=1
or,
x-2 = 9
x = 2
Hence, x=1 or x=2
Q.15. Solve the following quadratic equations by factorization: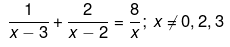
Ans.
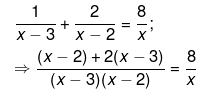
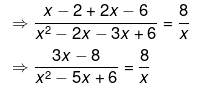
⇒ x(3x−8) = 8(x2−5x+6)
⇒ 3x2−8x=8x2−40x+48
⇒5x2−32x+48=0
⇒5x2−20x−12x+48=0
⇒5x(x−4)−12(x−4)=0
⇒(5x−12)(x−4)=0
⇒5x−12=0 or x−4=0
⇒x=125 or x=4
Hence, the factors are 4 and 12/5
Q.16. Solve the following quadratic equations by factorization:
a2x2 - 3abx + 2b2 = 0
Ans.
We have been given
a2x2 - 3abx + 2b2 = 0
a2x2 - 2abx - abx+2b2 = 0
ax(ax-2b) - b(ax-2b) = 0
(ax-b)(ax - 2b) = 0
Therefore,
ax - b = 0
ax= b
x = b/a
or,
ax - 2b = 0
ax = 2b
x = 2b/a
Hence,
x = b/a or x = 2b/a
Q.17. Solve the following quadratic equations by factorization:
9x2−6b2x−(a4−b4)=0
Ans.
9x2−6b2x−(a4−b4)=0
⇒9x2−6b2x−(a2−b2)(a2+b2)=0
⇒9x2+3(a2−b2)x−3(a2+b2)x−(a2−b2)(a2+b2)=0
⇒3x[3x+(a2−b2)]−(a2+b2)[3x+(a2−b2)]=0
⇒[3x−(a2+b2)][3x+(a2−b2)]=0
⇒3x−(a2+b2)=0 or 3x+(a2−b2)=0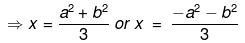
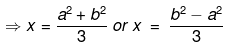
Hence, the factor are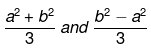
Q.18. Solve the following quadratic equations by factorization:
4x2+4bx−(a2−b2)=0
Ans.
We have been given
4x2 + 4bx - (a2 - b2) = 0
4x2 + 2(a + b)x-2(a-b)x-(a2 - b2) = 0
2x(2x+a+b) -(a-b)(2x+a+b) = 0
(2x-(a-b))(2x+a+b) = 0
Therefore,
2x-(a-b) = 0
2x = a-b
x = (a-b)/2
or,
2x+a+b = 0
2x = -(a + b)
x = (-a + b)/2
Hence,
x = (a-b)/2 or x = -(a+b)/2
Q.19. Solve the following quadratic equations by factorization:
ax2+(4a2−3b)x−12ab=0
Ans.
We have been given
ax2 + (4a2 -3b)x - 12ab = 0
ax2 +4a2x -3bx - 12ab = 0
ax(x+4a) - 3b(x+4a) = 0
(ax-3b)(x+4a) = 0
Therefore,
ax-3b = 0
ax = 3b
x = 3b/2
or,
x+4a = 0
x = -4a
Hence,
x = 3b/2 or x = -4a
Q.20. Solve the following quadratic equations by factorization:
2x2+ax−a2=0
Ans.
2x2+ax−a2=0
⇒ 2x2+2ax−ax−a2=0
⇒ 2x(x+a)−a(x+a)=0
⇒ (2x−a)(x+a)=0
⇒ 2x−a=0 or x+a=0
⇒ x = a/2 or x = -a
Hence, the factor are a/2 and -a
Q.21. Solve the following quadratic equations by factorization: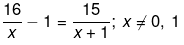
Ans.
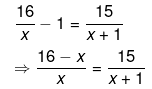
⇒ (16−x)(x+1)=15x
⇒ 16x+16−x2−x=15x
⇒ −x2+16+15x=15x
⇒ −x2+16=0
⇒ x2−16=0
⇒ (x−4)(x+4)=0
⇒ x−4=0 or x+4=0
⇒ x=4 or x=−4
Hence, the factors are 4 and −4.
Page No 4.20
Q.22. Solve the following quadratic equations by factorization: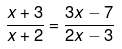
Ans.
We have been given
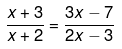
2x2 - 3x+6x - 9 = 3x2 - 7x+6x - 14
x2 - 4x - 5 = 0
x2 - 5x + x - 5 = 0
x(x-5)+1(x-5) = 0
(x+1)(x-5) = 0
Therefore,
x+1 = 0
x = -1
or,
x-5= 0
x = 5
Hence,
x = -1 or x = 5
Q.23. Solve the following quadratic equations by factorization: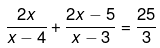
Ans.
We have been given
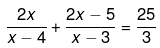
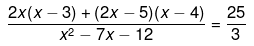
6x2 - 18x + 6x2 - 24x - 15x + 60 = 25x2 - 175x+300
13x2 - 118x + 240 = 0
13x2 -78x - 40x + 240
13x(x-6) - 40(x-6) = 0
(x-6)(13x-40) = 0
Therefore,
x-6= 0
x = 6
or,
13x - 40 = 0
13x = 40
x = 40/13
Hence,
x = 6 or x = 40/13
Q.24. Solve the following quadratic equations by factorization:
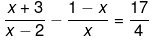
Ans.
We have been given
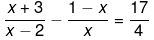
4(x2+3x-x+x2+2-2x) = 17(x2-2x)
9x2 - 34x - 8 = 0
9x2 - 36x + 2x - 8 = 0
9x(x-4)+2(x-4)=0
(9x+2)(x-4) = 0
Therefore,
9x+2 = 0
9x = -2
x = -2/9
or,
x-4 = 0
x= 4
Hence,
x = -2/9 or x = 4
Q.25. Solve the following quadratic equations by factorization: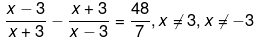
Ans.
We have been given
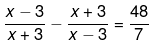
7(x2+9-6x-9- 6x) = 48(x2-9)
48x2 + 84x - 432 = 0
4x2 + 7x - 36 = 0
Therefore,
4x2+16x-9x - 36 = 0
4x(x+4) - 9(x+4) = 0
(4x - 9) (x+4) = 0
Therefore,
4x-9 =0
4x = 9
x = 9/4
or,
x+4 = 0
x = -4
Hence,
x = 9/4 or x = -4
Q.26. Solve the following quadratic equations by factorization: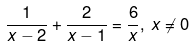
Ans.
We have been give
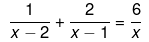
x2-x+2x2 - 4x = 6 (x2-x-2x+2)
3x2 - 13x + 12 = 0
Therefore,
3x2 - 9x - 4x + 12 = 0
3x(x-3) -4(x-3) = 0
(3x-4)(x-3) = 0
Therefore,
3x - 4 = 0
3x = 4
x = 4/3
or,
x-3 = 0
x = 3
Hence,
x = 4/3 or x = 3
Q.27. Solve the following quadratic equations by factorization: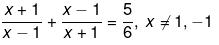
Ans.
We have been given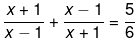
6(x2+1+2x-x2-1+2x) = 5(x2-1)
5x2 - 24x - 5 = 0
5x2 - 25x + x - 5 = 0
5x(x-5)+1(x-5) = 0
(5x+1) (x-5)=0
Therefore,
5x+1 = 0
5x = -1
x = -1/5
or,
x-5 = 0
x= 5
Hence,
x = -1/5 or x = 5
Q.28. Solve the following quadratic equations by factorization: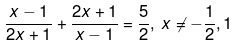
Ans.
We have been given
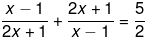
2(x2+1-2x+4x2+1+4x) = 5(2x2 - x-1)
10x2 + 4x+4 = 10x2- 5x - 5
9x+9 = 0
Therefore,
9x = -9
x = -9/9
x = -1
Hence,
x = -1
Q.29. Solve the following quadratic equations by factorization: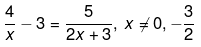
Ans.
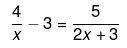
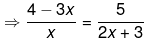
⇒(4−3x)(2x+3) = 5x
⇒8x+12−6x2−9x = 5x
⇒−6x2−6x+12=0
⇒x2+x−2 = 0
⇒x2+2x−x−2 = 0
⇒x(x+2)−1(x+2) = 0
⇒(x−1)(x+2) = 0
⇒x−1=0 or x+2 = 0
⇒x = 1 or x = −2
Hence, the factors are 1 and −2.
Q.30. Solve the following quadratic equations by factorization: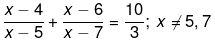
Ans.

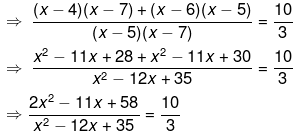
⇒ 3(2x2−22x+58) = 10(x2−12x+35)
⇒ 6x2−66x+174 = 10x2−120x+350
⇒ 4x2−54x+176 = 0
⇒ 2x2−27x+88 = 0
⇒ 2x2−11x−16x+88 = 0
⇒ x(2x−11)−8(2x−11) = 0
⇒ (x−8)(2x−11) = 0
⇒ x−8=0 or 2x−11=0
⇒ x = 8 or x = 11/2
Hence, the factors are 8 and 11/2.
Q.31. Solve the following quadratic equations by factorization: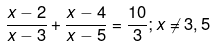
Ans.
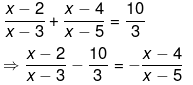
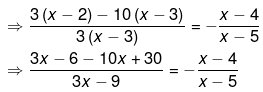
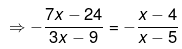
⇒ (7x−24)(x−5) = (3x−9)(x−4)
⇒ 7x2−59x+120 = 3x2−21x+36
⇒ 4x2−38x+84 = 0
⇒ 2x2−19x+42 = 0
⇒ 2x2−12x−7x+42 = 0
⇒ 2x(x−6)−7(x−6) = 0
⇒ (2x−7)(x−6) = 0
⇒ 2x−7=0 or x−6 = 0
⇒ x=72 or x = 6
Hence, the factors are 6 and 7/2
Q.32. Solve the following quadratic equations by factorization: 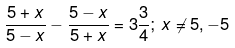
Ans.
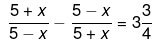
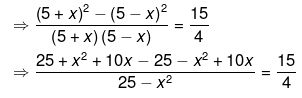
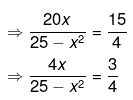 ⇒ 16x = 75−3x2
⇒ 16x = 75−3x2
⇒ 3x2+16x−75 = 0
⇒ 3x2+25x−9x−75 = 0
⇒ x(3x+25)−3(3x+25) = 0
⇒ (x−3)(3x+25) = 0
⇒ x−3 = 0 or 3x+25 = 0
⇒ x = 3 or x = -25/3
Hence, the factors are 3 and -25/3
Q.33. Solve the following quadratic equations by factorization: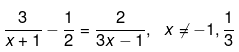
Ans.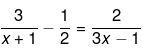
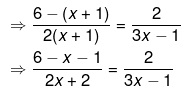
⇒ (5−x)(3x−1) = 2(2x+2)
⇒ 15x−5−3x2+x = 4x+4
⇒ −3x2+16x−5−4x−4 = 0
⇒ −3x2+12x−9 = 0
⇒ 3x2−12x+9 = 0
⇒ x2−4x+3 = 0
⇒ x2−3x−x+3 = 0
⇒ x(x−3)−1(x−3) = 0
⇒ (x−1)(x−3) = 0
⇒ x−1=0 or x−3 = 0
⇒ x=1 or x=3
Hence, the factors are 3 and 1.
Q.34. Solve the following quadratic equations by factorization: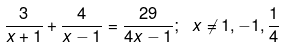
Ans.
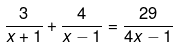
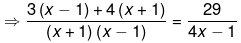
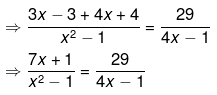
⇒ (7x+1)(4x−1) = 29(x2−1)
⇒ 28x2−7x+4x−1 = 29x2−29
⇒ 29x2−28x2+3x−28 = 0
⇒ x2+3x−28 = 0
⇒ x2+7x−4x−28 = 0
⇒ x(x+7)−4(x+7) = 0
⇒ (x−4)(x+7) = 0
⇒ x−4=0 or x+7 = 0
⇒ x = 4 or x = −7
Hence, the factors are 4 and −7.
Q.35. Solve the following quadratic equations by factorization: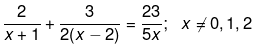
Ans.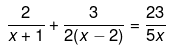

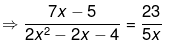
⇒ 5x(7x−5)=23(2x2−2x−4)
⇒ 35x2−25x=46x2−46x−92
⇒ 46x2−35x2−46x+25x−92 = 0
⇒ 11x2−21x−92 = 0
⇒ 11x2−44x+23x−92 = 0
⇒ 11x(x−4)+23(x−4) = 0
⇒ (11x+23)(x−4) = 0
⇒ 11x+23=0 or x−4 = 0
⇒ x = −23/11 or x = 4
Hence, the factors are 4 and -23/11.
FAQs on Chapter 4 - Quadratic Equations, RD Sharma Solutions - (Part-1) - Class 10
| 1. How do you solve quadratic equations using the quadratic formula? |  |
| 2. What are the methods to solve quadratic equations other than the quadratic formula? |  |
| 3. Can all quadratic equations be solved using the quadratic formula? |  |
| 4. How do you determine the nature of the roots of a quadratic equation using the discriminant? |  |
| 5. What are the real-life applications of quadratic equations? |  |














