Chapter 2 - Polynomials, RD Sharma Solutions - (Part-6) | RD Sharma Solutions for Class 10 Mathematics PDF Download
Page No 2.59
Ques.9. If the diagram in shows the graph of the polynomial f(x) = ax2 + bx + c, then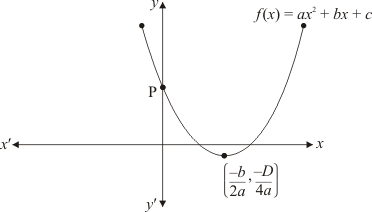
(a) a > 0, b < 0 and c > 0
(b) a < 0, b < 0 and c < 0
(c) a < 0, b > 0 and c > 0
(d) a < 0, b > 0 and c < 0
Ans. Clearly, f(x) = ax2 + bx + c represent a parabola opening upwards. 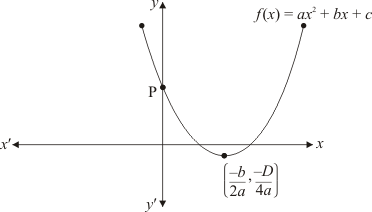
Therefore, a > 0 y = ax2 + bx + c cuts Y axis at P which lies on OY. Putting x = 0 in y = ax2 + bx + c, we get y = c. So the coordinates of P is (0, c). Clearly, P lies on OY. Therefore c > 0
Hence, the correct choice is a.
Ques.10. Show the graph of the polynomial f(x) = ax2 + bx + c for which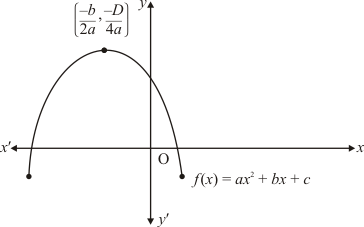
(a) a < 0, b > 0 and c > 0
(b) a < 0, b < 0 and c > 0
(c) a < 0, b < 0 and c < 0
(d) a > 0, b > 0 and c < 0
Ans. Clearly, f(x) = ax2 + bx + c represent a parabola opening downwards. Therefore, a < 0
y = ax2 + bx + c cuts y-axis at P which lies on OY. Putting x = 0 in y = ax2 + bx + c, we get y = c. So the coordinates P are (0, c). Clearly, P lies on(OY). Therefore c > 0
The vertex 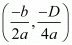 of the parabola is in the second quadrant. Therefore (-b)/2a < 0, b < 0
of the parabola is in the second quadrant. Therefore (-b)/2a < 0, b < 0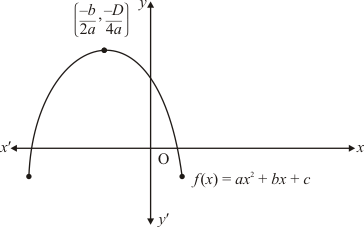
Therefore a < 0, b < 0, and c > 0
Hence, the correct choice is b.
Ques.11. If the product of zeros of the polynomial f(x) ax3 − 6x2 + 11x − 6 is 4, then a =
(a) 3/2
(b) -(3/2)
(c) 2/3
(d) -(2/3)
Ans. Since α and β are the zeros of quadratic polynomial f(x) = ax3 - 6x2 + 11x - 6
αβ = ((-Constant term)/(Coefficient of x2))
So we have
4 = -((-6)/a)
4 = 6/a
4a = 6
a = 6/4
a = 3/2
The value of a is 3/2
Hence, the correct alternative is a.
Ques.12. If zeros of the polynomial f(x) = x3 − 3px2 + qx − r are in A.P., then
(a) 2p3 = pq − r
(b) 2p3 = pq + r
(c) p3 = pq − r
(d) None of these
Ans. Let a - d, a, a + d be the zeros of the polynomial f(x) = x3 - 3px2 + qx -r then
Sum of zeros = ((-Coefficient of x2/Coefficient of x3)
(a - d) + a + (a + d) = (-(-3p))/1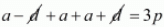
3a = 3p
a = (3/3)p
a = p
Since a is a zero of the polynomial f(x)
Therefore,
f(a) = 0
a3 - 3pa2 + qa - r = 0
Substituting a = p we get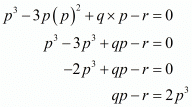
Hence, the correct choice is a.
Page No 2.60
Ques.13. If the product of two zeros of the polynomial f(x) = 2x3 + 6x2 − 4x + 9 is 3, then its third zero is
(a) 3/2
(b) -(3/2)
(c) 9/2
(d) -(9/2)
Ans. Let α, β, γ be the zeros of polynomial f(x) = 2x3 + 6x2 - 4x + 9 such that αβ = 3
We have,
αβγ = Constant term/Coefficient of x2
= (-9)/2
Putting αβ = 3 in αβγ = (-9)/2 , we get
αβγ = (-9)/2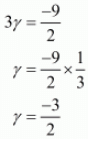
Therefore, the value of third zero is (-3)/2
Hence, the correct alternative is b.
Ques.14. If the polynomial f(x) = ax3 + bx − c is divisible by the polynomial g(x) = x2 + bx + c, then ab =
(a) 1
(b) 1/c
(c) -1
(d) -(1/c)
Ans. We have to find the value of ab
Given f(x) = ax3 + bx - c is divisible by the polynomial g(x) = x2 + bx + c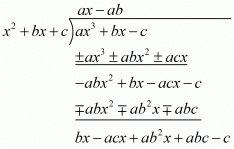
We must have
bx - acx + ab2x + abc - c = 0, for all x
So put x = 0 in this equation
x(b - ac + ab2) + c(ab - 1) = 0
c(ab - 1) = 0
Since c ≠ 0, so
ab - 1 = 0
⇒ ab = 1
Hence, the correct alternative is a.
Ques.15. If Q.No. 14, c =
(a) b
(b) 2b
(c) 2b2
(d) −2b
Ans. We have to find the value of c
Given f(x) = ax3 + bx - c is divisible by the polynomial g(x) = x2 + bx + c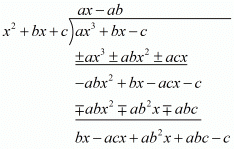
We must have
bx - acx + ab2x +abc - c = 0 for all x
x(b - ac + ab2) + c(ab - 1) = 0 ...(1)
c(ab - 1) = 0
Since c ≠ 0, so
ab - 1 = 0
ab = 1
Now in the equation (1) the condition is true for all x. So put x = 1 and also we have ab = 1
Therefore we have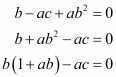
Substituting a = 1/b and ab = 1 we get,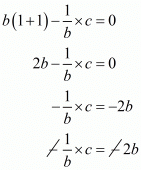
c = 2b x (b/1)
c = 2b2
Hence, the correct alternative is c.
Ques.16. If one root of the polynomial f(x) = 5x2 + 13x + k is reciprocal of the other, then the value of k is
(a) 0
(b) 5
(c) 1/6
(d) 6
Ans. If one zero of the polynomial f(x) = 5x2 + 13x + k is reciprocal of the other. So 
Now we have
α x β = Constant term/Coefficient of x2
= k/5
Since αβ = 1
Therefore we have
αβ = k/5
1 = k/5
⇒ k = 5
Hence, the correct choice is b.
Ques.17. If α, β, γ are the zeros of the polynomial f(x) = ax3 + bx2 + cx + d, then 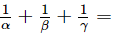
(a) −(b/d)
(b) c/d
(c) −(c/d)
(d) −(c/a)
Ans. We have to find the value of 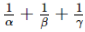
Given α, β, γ be the zeros of the polynomial f(x) = ax3 + bx2 + cx + d
We know that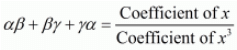
= c/a
= ((-d)/a)
So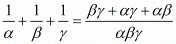
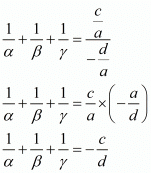
Hence, the correct choice is c.
Ques.18. If α, β, γ are the zeros of the polynomial f(x) = ax3 + bx2 + cx + d, then α2 + β2 + γ2 =
(a) 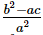
(b) 
(c) 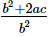
(d) 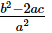
Ans. We have to find the value of α2 + β2 + γ2
Given α, β, γ be the zeros of the polynomial f(x) = ax3 + bx2 + cx + d
= ((-b)/a)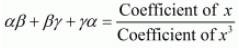
= c/a
Now
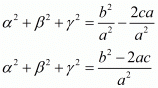
The value of 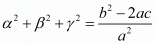
Hence, the correct choice is d.
Ques.19. If α, β, γ are are the zeros of the polynomial f(x) = x3 − px2 + qx − r, then 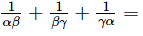
Ans. We have to find the value of 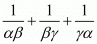
Given α, β, γ be the zeros of the polynomial f(x) = x3 - px2 + qx - r
α + β + γ = -Coefficient of x2/Coefficient of x3
= ((-p)/1)
= p
αβγ = -Constant term/Coefficient of x2
= ((-r))/1
= r
Now we calculate the expression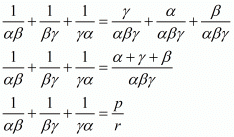
Hence, the correct choice is b.
Ques.20. If α, β are the zeros of the polynomial f(x) = ax2 + bx + c, then 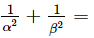
(a) 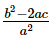
(b) 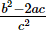
(c) 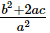
(d) 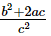
Ans. We have to find the value of 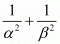
Given α and β are the zeros of the quadratic polynomial f(x) = ax2 + bx + c
α + β = -Coefficient of x/Coefficient of x3
= ((-b)/a)
αβ = Constant term/Coefficient of x2
= c/a
We have,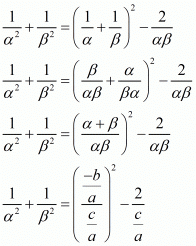
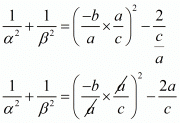
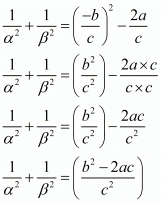
Hence, the correct choice is b.
Ques.21. If two of the zeros of the cubic polynomial ax3 + bx2 + cx + d are each equal to zero, then the third zero is
(a) ((−d)/a)
(b) c/a
(c) ((−b)/a)
(d) b/a
Ans. Let α = 0, β = 0 and γ be the zeros of the polynomial
f(x) = ax3 + bx2 + cx + d
Therefore
α + β + γ = ((-Coefficient of x2)/(Coefficient of x3)
= -(b/a)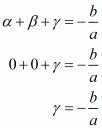
The value of γ = -(b/a)
Hence, the correct choice is c.
Ques.22. If two zeros x3 + x2 − 5x − 5 are √5 and −√5, then its third zero is
(a) 1
(b) −1
(c) 2
(d) −2
Ans. Let α = √5 and β = -√5 be the given zeros and be the third zero of x3 + x2 − 5x − 5 = 0 then
By using α + β + γ = ((-Coefficient of x2)/(Coefficient of x3)
α + β + γ = (+(+1))/1
α + β + γ = -1
By substituting α = √5 and β = -√5 in α + β + γ = -1
γ = -1
Hence, the correct choice is b.
Ques.23. The product of the zeros of x3 + 4x2 + x − 6 is
(a) −4
(b) 4
(c) 6
(d) −6
Ans. Given α, β, γ be the zeros of the polynomial f(x) = x3 + 4x2 + x - 6
Product of the zeros = Constant term/Coefficient of x3 = 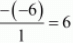
The value of Product of the zeros is 6.
Hence, the correct choice is c.
Page No 2.61
Ques.24. What should be added to the polynomial x2 − 5x + 4, so that 3 is the zero of the resulting polynomial?
(a) 1
(b) 2
(c) 4
(d) 5
Ans. If x = α, is a zero of a polynomial then x - α is a factor of f(x)
Since 3 is the zero of the polynomial f(x) = x2 - 5x + 4,
Therefore x - 3 is a factor of f(x)
Now, we divide f(x) = x2 - 5x + 4 by (x - 3) we get 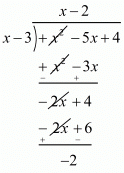
Therefore we should add 2 to the given polynomial
Hence, the correct choice is b.
Ques.25. What should be subtracted to the polynomial x2 − 16x + 30, so that 15 is the zero of the resulting polynomial?
(a) 30
(b) 14
(c) 15
(d) 16
Ans. We know that, if x = α, is zero of a polynomial then x - α is a factor of f(x)
Since 15 is zero of the polynomial f (x) = x2 − 16x + 30, therefore (x − 15) is a factor of f (x)
Now, we divide f (x) = x2 − 16x + 30 by (x - 15) we get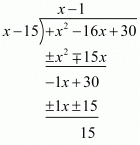
Thus we should subtract the remainder 15 from x2 - 16x + 30,
Hence, the correct choice is c.
FAQs on Chapter 2 - Polynomials, RD Sharma Solutions - (Part-6) - RD Sharma Solutions for Class 10 Mathematics
| 1. Can you explain the concept of polynomial division? |  |
| 2. How do you find the degree of a polynomial? |  |
| 3. What is the Remainder Theorem in polynomials? |  |
| 4. How can we determine if a polynomial is a factor of another polynomial? |  |
| 5. Can you explain the process of synthetic division in polynomial division? |  |

|
Explore Courses for Class 10 exam
|

|
















