Chapter 3 - Pair Of Linear Equations In Two Variables, RD Sharma Solutions - (Part-4) | RD Sharma Solutions for Class 10 Mathematics PDF Download

Page No 3.112

Q.14. Half the perimeter of a garden, whose length is 4 more than its width is 36 m. Find the dimension of the garden.
Ans. Let perimeter of rectangular garden will be 2(l + b). if half the perimeter of a garden will be 36 km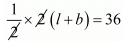

(l + b) = 36  ...(i)
When the length is four more than its width then (b + 4)
Substituting l = b + 4 in equation (i) we get
l + b = 36
b + 4 + b = 36
2b = 36 - 4
2b = 32
b = 32/2
b = 16
Putting b = 16 in equation (i) we get
(l + b) = 36
l + 16 = 36
l = 36 = 16
l = 20
Hence, the dimensions of rectangular garden are width = 16 m and length = 20m

Q.15. The larger of two supplementary angles exceeds the smaller by 18 degrees. Find them.
Ans. We know that the sum of supplementary angles will be 180°
Let the longer supplementary angles will be 'y',
Then, x + y = 180°  ...(i)
If larger of supplementary angles exceeds the smaller by 18 degree, According to the given condition. We have,
x = y + 18  ...(ii)
Substitute x = y + 18 in equation (i), we get,
x + y = 180°
y + 18 + y = 180°
2y + 18 = 180°
2y = 180° - 18°
2y = 162°
y = 162°/ 2
y = 81°
Put y = 81° equation (ii), we get,
x = y + 18
x = 81 + 18
x = 99°
Hence, the larger supplementary angle is 99°
The smaller supplementary angle is 81°

Q.16. 2 women and 5 men can together finish a piece of embroidery in 4 days, while 3 women and 6 men can finish it in 3 days. Find the time taken by 1 woman alone to finish the embroidery, and that taken by 1 man alone.
Ans. 1 women alone can finish the work in x days and 1 man alone can finish it in y days then
One woman one day work = 1/x
One man one days work = 1/y
2 women’s one days work = 2/x
5 man’s one days work = 5/y
Since 2 women and 5 men can finish the work in 4 days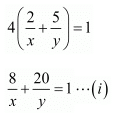

3 women and 6 men can finish the work in 3 days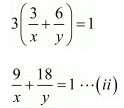

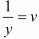Putting andin equation (i) and (ii) we get
8u + 20v - 1 = 0  ...(iii)
9u + 18v - 1 = 0  ...(iv)
By using cross multiplication we have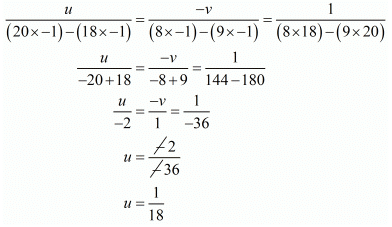


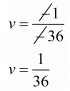
Now ,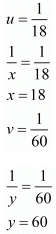

Hence, the time taken by 1 woman alone to finish the embroidery is 36 days.
The time taken by 1 man alone to finish the embroidery is 18 days.

Q.17. Meena went to a bank to withdraw Rs 2000. She asked the cashier to give her Rs 50 and Rs 100 notes only. Meena got 25 notes in all. Find how many notes Rs 50 and Rs 100 she received.
Ans. Let Rs. x be the notes of Rs. 50 and Rs. 100 notes will be Rs. y
If Meena ask for Rs. 50 and Rs. 100 notes only, then the equation will be,
50x + 100y = 2000
Divide both sides by 50 then we get,
x + 2y = 40 ...(i)
If Meena got 25 notes in all then the equation will be,
x + y = 25 ...(ii)
By subtracting the equation (ii) from (ii)we get,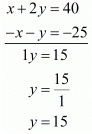

Substituting y = 15 in equation (ii), we get
x + y = 25
x + 15 = 25
x = 25 - 15
x = 10
Therefore x = 10 and y = 15
Hence, Meena has 10 notes of Rs. 50 and 15 notes of Rs. 100

Q.18. There are two examination rooms A and B. If 10 candidates are sent from A to B, the number of students in each room is same. If 20 candidates are sent from B to A, the number of students in A is double the number of students in B. Find the number of students in each room.
Ans. Let us take the A examination room will be x and the B examination room will be y
If 10 candidates are sent from A to B, the number of students in each room is same. According to the above condition equation will be
y + 10 = x - 10
0 = x - y - 10 - 10
x - y - 20 = 0  ...(i)
If 20 candidates are sent from B to A, the number of students in A is double the number of students in B, then equation will be,
x + 20 = 2(y - 20)
x + 20 = 2y - 40
x + 20 - 2y + 40 = 0
x - 2y + 60 = 0 ...(ii)
By subtracting the equation (i) from (ii) we get, y = 80
Substituting y = 80 in equation (i), we get
Hence 100 candidates are in A examination Room,
80 candidates are in B examination Room.

Q.19. A railway half ticket costs half the full fare and the reservation charge is the same on half ticket as on full ticket. One reserved first class ticket from Mumbai to Ahmedabad costs Rs 216 and one full and one half reserved first class tickets cost Rs 327. What is the basic first class full fare and what is the reservation charge?
Ans. Let take first class full of fare is Rs x and and reservation charge is Rs y per ticket
Then half of the ticket as on full ticket = x/2
According to the given condition we have
x + y = 216  ...(i)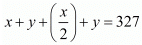



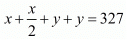
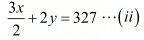
Multiplying equation (i) by 2 we have
2x + 2y = 432 ...(iii)
Subtracting (ii) from (iii) we get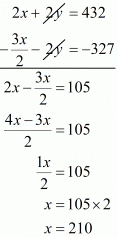

Putting x = 210 in equation (i) we get
x + y = 216
210 + y = 216
y = 216 - 210
y = 6
Hence, the basic first class full fare is Rs 210
The reservation charge is Rs. 6

Q.20. A wizard having powers of mystic in candations and magical medicines seeing a cock, fight going on, spoke privately to both the owners of cocks. To one he said; if your bird wins, than you give me your stake-money, but if you do not win, I shall give you two third of that'. Going to the other, he promised in the same way to give three fourths. From both of them his gain would be only 12 gold coins. Find the the stake of money each of the cock-owners have.
Ans. Let the strike money of first cock-owner be Rs. x and of second cock-owner be Rs. y respectively. Then we have,

For second cock-owner according to given condition we have,

By subtracting (ii) from (i) we have,

Putting x = 42 in equation (ii) we get,
3y - 2x = 36
3y - 2 x 42 = 36
3y - 84 = 36
3y = 36 + 84
3y = 120

y = 40
Hence the stake of money first cock-owner is Rs.42 and of second cock-owner is Rs. 40 respectively.

Q.21. The students of a class are made to stand in rows. If 3 students are extra in a row, there would be 1 row less. If 3 students are less in a row there would be 2 rows more. Find the number of student in the class.
Ans. Let the number of students be x and the number of row be y then,
Number of students in each row  = x/y
Where three students is extra in each row, there are one row less that is when each row has  students the number of rows is (y - 1)
Total number of students =no. of rows x no. of students in each row

If three students are less in each row then there are 2 rows more that is when each row has
Therefore, total number of students = Number of rows x Number of students in each row

Putting in (i) and  equation we get
- u + 3y - 3 = 0 ...(iii)
2u - 3y - 6 = 0 ...(iv)
Adding (iii) and equation we get(iv) 

Putting u = 9 in equation (iii)  we get
- u + 3y - 3 = 0
- 9 + 3y - 3 = 0
+ 3y - 12 = 0
3y - 12 = 0
3y = 12
y = 12/3
y = 4
u = 9
x/y = 9
x = 9 x 4
 x = 36
Hence, the number of students in the class is 36

Q.22. One says. "give me hundred, friend! I shall then become twice as rich as you" The other replies, "If you give me ten, I shall be six times as rich as you". Tell me what is the amount of their respective capital?
Ans. Let the money with first person be Rsx and the money with the second person be Rsy. then,
(x + 100) = 2 (y - 100)
(y + 10) = 6 (x - 10)
If first person gives Rs 100 to to second person then the second person will become twice as rich as first person, According to the given condition, we have,
(x + 100) = 2(y - 100)
x + 100 = 2y - 200
x - 2y + 100 + 200 = 0
x - 2y + 300 = 0 ...(i)
if second person gives  to first person then the first person will becomes six times as rich as second person, According to given condition, we have,
(y + 10) = 6 (x - 10)
y + 10 = 6 x - 10
0 = 6x - y - 70  ...(ii)
Multiplying (ii) equation by 2 we get
12x = 2y - 140 = 0  ...(iii)
By subtracting (iii) from (i), we get

Putting x = 40 in equation (i) we get,
x - 2y + 300 = 0
40 - 2y + 300 = 0
- 2y + 340 = 0

Hence, first person’s capital will be Rs. 40
Second person’s capital will be Rs. 170.

Q.23. A shopkeeper sells  a saree at 8% profit and a sweater at 10%
discount, thereby getting a sum of Rs.1008. If she had sold the saree at 10% profit and the sweater at 8% discount , she would have got Rs. 1028 . Find the cost price of the saree and the list price (price before discount) of the sweater.
Ans. Let the CP of saree be Rsx and the list price of sweater be Rs. y.
Case I: When saree is sold at 8% profit and sweater at 10% discount.
SP = CP + Profit
⇒ SP of saree = x +
SP of sweater = List price − Discount
⇒ SP of sweater =
Total sum received by the shopkeeper = Rs 1008

⇒ 108x + 90y = 100800
⇒ 6x + 5y = 5600            .....(i)
Case II: When saree is sold at 10% profit and sweater at 8% discount.
⇒ SP of saree =
SP of sweater = List price − Discount
⇒ SP of sweater =
SP of sweater = List price − Discount
⇒ SP of sweater =
Total sum received by the shopkeeper = Rs. 1028

Multiplying (i) by 110 and (ii) by 6, we get
660x + 550y = 616000                .....(iii)
660x + 552y = 616800                .....(iv)
Subtracting (iii) from (iv), we get
2y = 800
⇒ y = 400
Putting y = 400 in (i), we get
6x + 2000 = 5600
⇒ 6x = 5600 − 2000 = 3600
⇒ x = 600
Hence, CP of saree = Rs.600 and list price of sweater = Rs.400.

Q.24. In a competitive examination , one mark is awarded for each correct answer while 1/2 mark is deducted for everey wrong answer . Jayanti answered 120 questions and got 90 marks. How many questions did she answer correctly.
Ans. Let the number of correct answers be x and the number of wrong answers be y.
Total questions Jayanthi answered = 120
So, x + y = 120          .....(i)
Now, marks obtained for answering correctly = 1 × x = x
Marks deducted for answering incorrectly =
Total marks obtained = .....(ii)
Subtracting (ii) from (i), we get

Putting y = 20 in (i), we get
x + 20 = 120
⇒ x = 100
Thus, Jayanti answered 100 questions correctly.