Chapter 1 - Real Numbers, RD Sharma Solutions - (Part - 6) | RD Sharma Solutions for Class 10 Mathematics PDF Download

Page No 1.39

Q.1. Find the LCM and HCF of the following pairs of integers and verify that LCM × HCF = Product of the integers:
(i) 26 and 91
Ans. Let us first find the factors of 26 and 91
26 = 2 x 13
91 = 7 x 13
L.C.M of 26, and 91 = 2 x 7 x 13
L.C.M of 26, and 91 = 182
H.C.F of 26, and 91 = 13
We know that,
L.C.M × H.C.F = First number × Second number
⇒ 182 × 13 = 26 × 91
⇒ 2366 = 2366
Hence verified

(ii) 510 and 92
Ans. Let us first find the factors of 510 and 92
510 = 2 x 3 x 5 x 17
92 = 2² x 23
L.C.M of 510 and 92 = 2² x 3 x 5 x 23 x 17
L.C.M of 510 and 92 = 23460
H.C.F of 510 and 92 = 2
We know that,
L.C.M × H.C.F = First number × Second number
23460 x 2 = 510 x 92
46920 = 46920
Hence verified

(iii) 336 and 54
Ans. Let us first find the factors of 336 and 54
336 = 2⁴ x 3 x 7
54 = 2 x 3³
L.C.M of 336 and 54 = 2⁴ x 3³ x 7
L.C.M of 336 and 54 = 3024
H.C.F of 336 and 54 = 6
We know that,
L.C.M × H.C.F = First number × Second number
3024 x 6 = 336 x 54
18144 = 18144
Hence verified

(iv) 404 and 96
Ans. 404 = 2 × 2 × 101
96 = 2 × 2 × 2 × 2 × 2 × 3
LCM = 2 × 2 × 2 × 2 × 2 × 3 × 101 = 9696
LCM = 9696
HCF = 2 × 2 = 4
Product of numbers = 96 × 404 = 38784
LCM × HCF = 4 × 9696 = 38784
Hence, LCM × HCF = Product of numbers

Q.2. Find the LCM and HCF of the following integers by applying the prime factorisation method:
(i) 12, 15 and 21 
Ans. Let us first find the factors of 15, 12 and 21
12 = 2² x 3
15 = 3 x 5
21 = 3 x 7
L.C.M of 12, 15 and 21 = 2² x 3 x 5 x 7
L.C.M of 12, 15 and 21 = 420
H.C.F of 12, 15 and 21 = 3

(ii) 17, 23 and 29
Ans. Let us first find the factors of 17, 23 and 29
17 = 1 x 17
23 = 1 x 23
29 = 1 x 29
L.C.M of 17, 23 and 29 = 1 x 17 x 23 x 29
L.C.M of 17, 23 and 29 = 11339
H.C.F of 17, 23 and 29 = 1

(iii) 8, 9 and 25
Ans. Let us first find the factors of 8, 9 and 25
8 = 2³
9 = 3²
25 = 5²
L.C.M of 8, 9 and 25 = 2³ x 3² x 5²
L.C.M of 8, 9 and 25 = 1800
H.C.F of 8, 9 and 25 = 1

(iv) 40, 36 and 126
Ans. Let us first find the factors of 40, 36 and 126
40 = 2³ x 5
36 = 2² x 3²
126 = 2 x 3² x 7
L.C.M of 40, 36 and 126 = 2³ x 3^{2 x} 5 x 7
L.C.M of 40, 36 and 126 = 2520
H.C.F of 40, 36 and 126 = 2

(v) 84, 90 and 120
Ans. Let us first find the factors of 84, 90 and 120
84 = 2² x 3 x 7
90 = 2 x 3² x 5
120 = 2³ x 3 x 5
L.C.M of 84, 90 and 120 = 2² x 3² x 5 x 7
L.C.M of 84, 90 and 120 = 2520
H.C.F of 84, 90 and 120 = 6
(vi) 24, 15 and 36
Ans. Let us first find the factors of 24, 15 and 36.
24 = 2³ x 3
15 = 3 x 5
36 = 2² x 3²
L.C.M of 24, 15 and 36 = 2³ x 3² x 5
L.C.M of 24, 15 and 36 = 360
H.C.F of 24, 15 and 36 = 3

Q.3. (i) Given that HCF (306, 657) = 9, find LCM (306, 657).
Ans. GIVEN: H.C.F of two numbers 306 and 657 is 9.
TO FIND: L.C.M of number
We know that,
L.C.M x H.C.F = First Number x Second Number
L.C.M x 9 = 306 x 657
L.C.M = (306 x 657)/9
L.C.M = 22338

(ii) Write the smallest number which is divisible by both 306 and 657. 
Ans. The smallest number divisible by both 306 and 657 is the L.C.M of 306 and 657.
306 = 2 × 3 × 3 × 17
657 = 3 × 3 × 73
Therefore, L.C.M of 306 and 657 is 2 × 3 × 3 × 17 × 73 = 22,338
Hence, the smallest number which is divisible by both 306 and 657 is 22,338.

Page No 1.40

Q.4. Can two numbers have 16 as their HCF and 380 as their LCM? Give reason. 
Ans. TO FIND: can two numbers have 16 as their H.C.F and 380 as their L.C.M 
On dividing 380 by 16 we get 23 as the quotient and 12 as the remainder,
Since L.C.M is not exactly divisible by the H.C.F, two numbers cannot have 16 as their H.C.F and 380 as their L.C.M

Q.5. The HCF of two numbers is 145 and their LCM is 2175. If one number is 725, find the other. 
Ans. GIVEN: L.C.M and H.C.F of two numbers are 2175 and 145 respectively. If one number is 725
TO FIND: Other number
We know that,
L.C.M x H.C.F = First Number x Second Number
2175 x 145 = 725 x Second Number
Second Number = (2175 x 145)/725
Second Number = 435

Q.6. The HCF to two numbers is 16 and their product is 3072. Find their LCM. 
Ans. GIVEN: H.C.F of two numbers is 16. If product of numbers is 3072
TO FIND: L.C.M of numbers
We know that,
L.C.M x H.C.F = First Number x Second Number
L.C.M x 16 = 3072
L.C.M = 3072/16

Q.7. The LCM and HCF of two numbers are 180 and 6 respectively. If one of the numbers is 30, find the other number.
Ans. GIVEN: LCM and HCF of two numbers are 180 and 6 respectively. If one number is 30
TO FIND: Other number
We know that,
L.C.M x H.C.F = First Number x Second Number
180 x 6 = 30 x Second Number
Second Number = (180 x 6)/30
Second Number = 36

Q.8. Find the smallest number which when increased by 17 is exactly divisible by both 520 and 468.
Ans. TO FIND: Smallest number which when increased by 17 is exactly divisible by both 520 and 468.
L.C.M OF 520 and 468
520 = 2³ × 5 × 13
468 = 2² x 3² x 13
L.C.M of 520 and 468 = 2³ × 3² × 5 × 13 = 4680
Hence 4680 is the least number which exactly divides 520 and 468 i.e. we will get a remainder of 0 in this case. But we need the Smallest number which when increased by 17 is exactly divided by 520 and 468.
Therefore
= 4680 - 17
= 4663
Hence 4663 is Smallest number which when increased by 17 is exactly divisible by both 520 and 468.

Q.9. Find the smallest number which leaves remainders 8 and 12 when divided by 28 and 32 respectively. 
Ans. TO FIND: The smallest number which leaves remainders 8 and 12 when divided by 28 and 32 respectively.
L.C.M of 28 and 32.
28 = 2² x 7
32 = 2⁵
L.C.M of 28 and 32 = 2⁵ x 7
= 224
Hence 224 is the least number which exactly divides 28 and 32 i.e. we will get a remainder of 0 in this case. But we need the smallest number which leaves remainders 8 and 12 when divided by 28 and 32 respectively
Therefore
= 224 - 8 - 12
= 204
Hence 204 is the smallest number which leaves remainders 8 and 12 when divided by 28 and 32 respectively.

Q.10. What is the smallest number that, when divided by 35, 56 and 91 leaves remainders of 7 in each case?
Ans. TO FIND: Smallest number that, when divided by 35, 56 and 91 leaves remainder of 7 in each case
L.C.M OF 35, 56 and 91
35 = 5 x 7
56 = 2³ x 7
91 = 13 x 7
L.C.M OF 35, 56 and 91 = 2³ x 5 x 7 x 13
= 3640
Hence 84 is the least number which exactly divides 28, 42 and 84 i.e. we will get a remainder of 0 in this case. But we need the smallest number that, when divided by 35, 56 and 91 leaves remainder of 7 in each case
Therefore
= 3640 + 7
= 3647
Hence 3647 is smallest number that, when divided by 35, 56 and 91 leaves remainder of 7 in each case.

Q.11. A rectangular courtyard is 18 m 72 cm long and 13 m 20 cm broad. it is to be paved with square tiles of the same size. Find the least possible number of such tiles. 
Ans. GIVEN: A rectangular yard is 18 m 72 cm long and 13 m 20 cm broad .It is to be paved with square tiles of the same size.
TO FIND: Least possible number of such tiles.
Length of the yard = 18 m 72 cm = 1800 cm  + 72 cm = 1872 cm (∵ 1 m = 100cm)
Breadth of the yard =13 m 20 cm = 1300 cm + 20 cm = 1320 cm
The size of the square tile of same size needed to the pave the rectangular yard is equal the H.C.F of the length and breadth of the rectangular yard.
Prime factorisation of 1872 = 2⁴ ×3² × 13
Prime factorisation of 1320 = 2³ ×3 × 5 × 11
H.C.F of 1872 and 1320 = 2³ × 3 = 24
∴ Length of side of the square tile = 24 cm
Number of tiles required =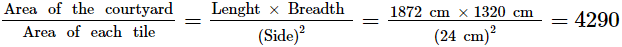 
Thus, the least possible number of tiles required is 4290. 

Q.12. Find the greatest number of 6 digits exactly divisible by 24, 15 and 36.
Ans. TO FIND: Greatest number of 6 digits exactly divisible by 24, 15 and 36
The greatest 6 digit number be 999999
24, 15 and 36
24 = 2³ x 3
15 = 3 x 5
36 = 2² x 3²
L.C.M OF 24, 15 and 36 = 360
Since 999999 / 360 = 2777 x 360 + 279
Therefore, the remainder is 279.
Hence the desired number is equal to
= 999999 - 279
= 999720
Hence 999720 is the greatest number of 6 digits exactly divisible by 24, 15 and 36.

Q.13. Determine the number nearest to 110000 but greater than 100000 which is exactly divisible by each of 8, 15 and 21.
Ans. TO FIND: The number nearest to 110000 but greater than 100000 which is exactly divisible by each of 8, 15 and 21.
L.C.M Of 8, 15 and 21.
8 = 2³
15 = 3 x 5
21 = 3 x 7
L.C.M OF 8, 15 and 21 = 2³ x 3 x 5 x 7 = 840
When 110000 is divided by 840, the remainder is obtained as 800.
Now, 110000 − 800 = 109200 is divisible by each of 8, 15 and 21.
Also, 110000 + 40 = 110040 is divisible by each of 8, 15 and 21.
109200 and 110040 are greater than 100000.
Hence, 110040 is the number nearest to 110000 but greater than 100000 which is exactly divisible by each of 8, 15 and 21.