Chapter 3 - Pair Of Linear Equations In Two Variables, RD Sharma Solutions - (Part-5) | RD Sharma Solutions for Class 10 Mathematics PDF Download
Page No 3.113
Q.1. The value of k for which the system of equations has a unique solution, is
kx − y = 2
6x − 2y = 3
(a) =3
(b) ≠3
(c) ≠0
(d) =0
Ans. The given system of equations are
kx - y = 2
6x - 2y = 3 for unique solution
for unique solution
Here a1 = k, a2 = 6, b1 = -1, b2 = - 2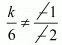
By cross multiply we get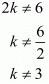
Hence, the correct choice is b.
Q.2. The value of k for which the system, of equations has infinite number of solutions, is
2x + 3y = 5
4x + ky = 10
(a) 1
(b) 3
(c) 6
(d) 0
Ans. The given system of equations are
2x + 3y = 5
4x + ky = 10
For the equations to have infinite number of solutions, 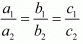
Here, a1 = 2, a2 = 4, b1 = 3, b2 = k
Therefore
By cross multiplication of  we get,
we get,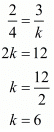
and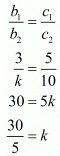
6 = k
Therefore the value of k is 6
Hence, the correct choice is c.
Q.3. The value of k for which the system of equations x + 2y − 3 = 0 and 5x + ky + 7 = 0 has no solution, is
(a) 10
(b) 6
(c) 3
(d) 1
Ans. The given system of equations are
x + 2y - 3 = 0
For the equations to have no solutions,
If we take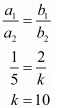
Therefore the value of k is10.
Hence, correct choice is a.
Page No 3.114
Q.4. The value of k for which the system of equations 3x + 5y = 0 and kx + 10y = 0 has non-zero solution, is
(a) 0
(b) 2
(c) 6
(d) 8
Ans. The given system of equations are,
3x + 5y = 0
kx + 10y = 0
Here, a1 = 3, a2 = k, b1 = 5, b2 = 10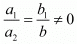
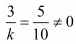
By cross multiply we get
30 = 5k
30/ 5 = k
6 = k
Therefore the value of k is 6,
Hence, the correct choice is c.
Q.5. If the system of equations has infinitely many solutions, then
2x + 3y = 7
(a + b)x + (2a − b)y = 21
(a) a = 1, b = 5
(b) a = 5, b = 1
(c) a = −1, b = 5
(d) a = 5, b = −1
Ans. The given systems of equations are
2x + 3y = 7
(a + b)x + (2a − b)y = 21
For the equations to have infinite number of solutions, 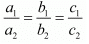
Here a1 = 2, a2 = (a + b), b1 = 3, b2 = 2a - b, c1 = 7, c2 = 21,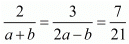
Let us take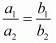
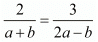
By cross multiplication we get,
2(2a - b) = 3 (a + b)
4a - 2b = 3a + 3b
4a - 3a = 3b + 2b
a = 5b ...(i)
Now take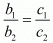
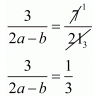
By cross multiplication we get,
3 x 3 = 1 x 2a - b
9 = 2a - b ...(ii)
Substitute a = 5b in the above equation
9 = 2 x 5b - b
9 = 10b - b
9 = 9b
9/9 = b
1 = b
Substitute b = 1 in equation (i) we get, a = 5b
a = 5 x 1
a = 5
Therefore a = 5 and b = 1
Hence, the correct choice is b.
Q.6. If the system of equations is inconsistent, then k =
3x+y=1
(2k−1)x+(k−1)y=2k+1
(a) 1
(b) 0
(c) −1
(d) 2
Ans. The given system of equations is inconsistent,
3x+y=1
(2k − 1) x + (k − 1)y = 2k + 1
If the system of equations is in consistent, we have
a1 - b2 - a2 b1 = 0
3x (k − 1) - 1 (2k − 1) = 0
3k - 3 - 2k + 1 = 0
1k = 2
Therefore, the value of k is 2.
Hence, the correct choice is d.
Q.7. If am ≠ bl, then the system of equations
ax + by = c
(a) has a unique solution
(b) has no solution
(c) has infinitely many solutions
(d) may or may not have a solution
Ans. Given am ≠ bl, the system of equations has
ax + by = c
lx + my = n
We know that intersecting lines have unique solution 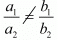
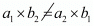
Here a1 = a, a2 = l, b1 = b, b2 = m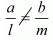
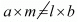
Therefore intersecting lines, have unique solution
Hence, the correct choice is a.
Q.8. If the system of equations has infinitely many solutions, then
2x + 3y = 7
2ax + (a+b)y = 28
(a) a = 2b
(b) b = 2a
(c) a + 2b = 0
(d) 2a + b = 0
Ans. Given the system of equations are
2x + 3y = 7
2ax + (a + b)y = 28
For the equations to have infinite number of solutions,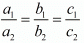
a1 = 2, a2 = 2a, b1 = 3, b2 = a + b
By cross multiplication we have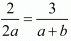
2 (a + b) = 2a (3)
2a + 2b = 6a
2b = 6a - 2a
2b = 4a
Divide both sides by 2. we get b = 2a
Hence, the correct choice is b.
Q.9. The value of k for which the system of equations has no solution is
x + 2y = 5
3x + ky + 15 = 0
(a) 6
(b) −6
(c) 3/2
(d) None of these
Ans. The given system of equation is
x + 2y = 5
3x + ky + 15 = 0
If  then the equation have no solution.
then the equation have no solution.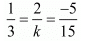
By cross multiply we get
k x 1 = 3 x 2
k = 6
Hence, the correct choice is a.
Q.10. If 2x − 3y = 7 and (a + b)x − (a + b − 3)y = 4a + b represent coincident lines, then a and b satisfy the equation
(a) a + 5b = 0
(b) 5a + b = 0
(c) a − 5b = 0
(d) 5a − b = 0
Ans. The given system of equations are
2x - 3y = 7
(a + b)x − (a + b − 3)y = 4a + b
For coincident lines , infinite number of solution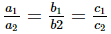
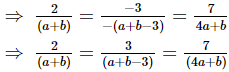
⇒ 2(a + b − 3) = 3(a + b)
⇒ 2a + 2b − 6 = 3a + 3b
⇒ 2a + 2b − 3a − 3b = 6
⇒ − a − b = 6
⇒ a+b=−6 −−−(i)
3(4a + b) = 7(a + b − 3)
⇒12a + 3b = 7a + 7b − 21
⇒5a − 4b = −21 −−−(ii)
multiply equation (i) by 5, we get 5a + 5b=−30 −−−(iii)
subtract (ii) from (iii),
(5a + 5b) − (5a − 4b) = −30 + 21
⇒ 5a + 5b − 5a + 4b = −9
⇒ 9b = −9
⇒b = −1
substitute b=−1 in equation (1)
a + (−1) = −6
⇒ a = −6 + 1 = −5
Option A.:
a + 5b = 0
−5 + 5(−1) = −5 − 5 = −10 ≠ 0
Option B:
5a + b = 0
5 (−5) + (−1) = −25 − 1 = −26 ≠ 0
Option.C:
a - b = 0
-5 - (-1) = -4 ≠ 0
None of the option satisfies the values.
Q.11. If a pair of linear equations in two variables is consistent, then the lines represented by two equations are
(a) intersecting
(b) parallel
(c) always coincident
(d) intersecting or coincident
Ans. If a pair of linear equations in two variables is consistent, then its solution exists.
∴The lines represented by the equations are either intersecting or coincident.
Hence, correct choice is d.
Q.12. The area of the triangle formed by the line 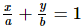 with the coordinate axes is
with the coordinate axes is
(a) ab
(b) 2ab
(c) 1/2 ab
(d) 1/4 ab
Ans. Given the area of the triangle formed by the line 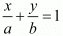
If in the equation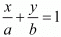 either A and B approaches infinity, The line become parallel to either x axis or y axis respectively,
either A and B approaches infinity, The line become parallel to either x axis or y axis respectively,
Therefore
x = a;
y = b;
Area of triangle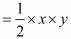
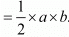
Hence, the correct choice is c.
Q.13. The area of the triangle formed by the lines y = x, x = 6 and y = 0 is
(a) 36 sq. units
(b) 18 sq. units
(c) 9 sq. units
(d) 72 sq. units
Ans. Given x = 6, y = 0 and x = y
We have plotting points as (6,0) (0,0) (6,6) when x = y
Therefore, area of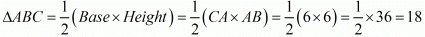
Area of triangle ABC is 18 square units
Hence, the correct choice is b.
Page No 3.115.
Q.14. If the system of equations 2x + 3y = 5, 4x + ky = 10 has infinitely many solutions, then k =
(a) 1
(b) ½
(c) 3
(d) 6
Ans. The given system of equations
2x + 3y = 5
4x + ky = 5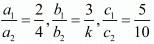
For the equations to have infinite number of solutions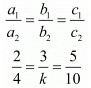
If we take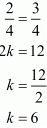
And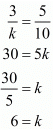
Therefore, the value of k is 6.
Hence, the correct choice is d.
Q.15. If the system of equations kx − 5y = 2, 6x + 2y = 7 has no solution, then k =
(a) −10
(b) −5
(c) −6
(d) −15
Ans. The given systems of equations are
kx - 5y = 2
6x + 2y = 7
If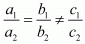
Here a1 = k, a2 = 6, b1 = - 5, b2 = 2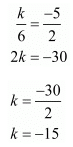
Hence, the correct choice is d.
Q.16. The area of the triangle formed by the lines x = 3, y = 4 and x = y is
(a) ½ sq. unit
(b) 1 sq. unit
(c) 2 sq. unit
(d) None of these
Ans. Given x = 3, y = 4 and x = y
We have plotting points as (3,4)(3,3)(4,4) when x = y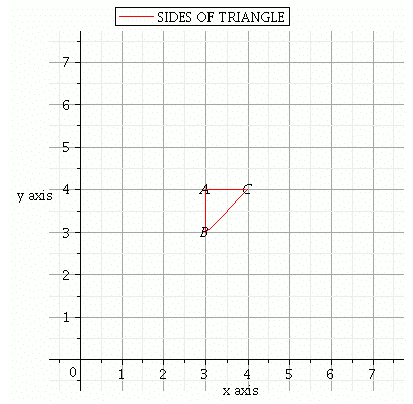
Therefore, area of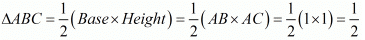
Area of triangle ABC is 1/2 square units
Hence, the correct choice is a.
Q.17. The area of the triangle formed by the lines 2x + 3y = 12, x − y − 1 = 0 and x = 0 (as shown in Fig. 3.23), is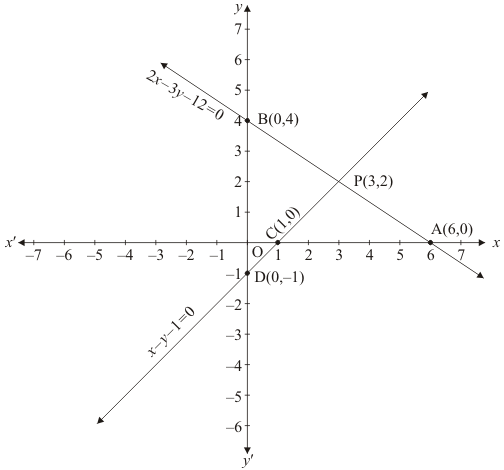
(a) 7 sq. units
(b) 7.5 sq. units
(c) 6.5 sq. units
(d) 6 sq. units
Ans. Given 2x + 3y = 12, x - y = 0 and x = 0
If x = 0 We have plotting points as D(0, -1)B(0,4)P(3,2)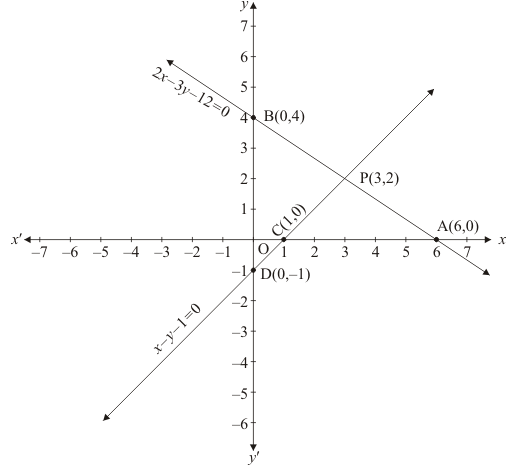
Therefore, area of
Area of triangle ABC is 7.5 square units
Hence, the correct choice is b.
Page No 3.115
Q.18. The sum of the digits of a two digit number is 9 . If 27 is added to it , the digits of the number get reversed. the number is
(a) 25
(b) 72
(c) 63
(d) 36
Ans. Let the digits at the tens and the ones place be x and y, respectively. So, the two digit number is 10x + y.
Now,
x + y = 9 .....(i)
Also,
10x + y + 27 = 10y + x
⇒ 9x − 9y = −27
⇒ x − y = −3 .....(ii)
Adding (i) and (ii), we get
2x = 6
⇒ x = 3
Putting x = 3 in (i), we get
3 + y = 9
⇒ y = 6
Thus, the required number is 10 × 3 + 6 = 36.
Hence, the correct answer is option (d).
Q.19. If x = a, y = b is the solution of the systems of equations x − y = 2 and x + y = 4 , then the values of a and b are, respectively
(a) 3 and 1
(b) 3 and 5
(c) 5 and 3
(d) − 1 and −3
Ans. The given equations are
x − y = 2 .....(1)
x + y = 4 .....(2)
Adding (1) and (2), we get
2x = 6
⇒ x = 3
Putting x = 3 in (1), we get
3 + y = 4
⇒ y = 1
So, x = a = 3 and y = b = 1.
Thus, the values of a and b are 3 and 1, respectively.
Hence, the correct answer is option (a).
Q.20. For what value k, do the equations 3x − y + 8 = 0 and 6x − ky + 16 = 0 reperesent coincident lines ?
(a) 1/2
(b)
(c) 2
(d) - 2
Ans. The given system of equations is
3x − y + 8 = 0
6x − ky + 16 = 0
We know that the lines
a1x + b1y + c1 = 0
a2x+b2y+c2=0
are coincident iff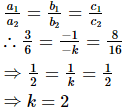
Thus, the value of k = 2.
Hence, the correct answer is option (c).
Page No 3.116
Q.21. Aruna has only Rs.1 and Rs.2 coins with her . If the total number of coins that she has is 50 and the amount of money with her is Rs.75 , then the number of Rs.1 and Rs.2 coins are , respectively
(a) 35 and 15
(b) 35 and 20
(c) 15 and 35
(d) 25 and 25
Ans. Let the number of Rs.1 coins be x and that of Rs.2 coins be y.
Now,
Total number of coins = 50
So, x + y = 50 .....(i)
Also,
Rs.1 × x + Rs.2 × y = Rs.75
∴ x + 2y = 75 .....(ii)
Subtracting (i) from (ii), we get
y = 25
Putting y = 25 in (i), we get
x + 25 = 50
⇒ x = 25
So, the number of Rs.1 coins and Rs.2 coins are 25 and 25, respectively.
Hence, the correct answer is option (d).
Disclaimer: The answer given in the book does not match with the one obtained.
Page No 3.116
Q.1. The pair of equations y = 0 and y = –7 has _________ solution.
Ans. The equation y = 0 is the x-axis and y = –7 is the line parallel to x-axis.
Therefore, both the lines are parallel lines.
Hence, the pair of equations y = 0 and y = –7 has no solution.
Q.2. The pair of equations x = a and y = b has solution ________.
Ans. The equation x = a is the line parallel to y-axis and y = b is the line parallel to x-axis.
Therefore, both the lines intersect each other.
The point of intersection is x = a and y = b i.e. (a, b).
Hence, the pair of equations x = a and y = b has solution (a, b).
Q.3. If the pair of equations 3x + 2ky = 2 and 2x + 5y + 1 = 0 has no solution, then k = _________.
Ans. If the system of equations a1x+b1y+c1=0 and a2x+b2y+c2=0 has no solution, then
Since, the system of equations 3x + 2ky = 2 and 2x + 5y + 1 = 0 has no solution
Therefore,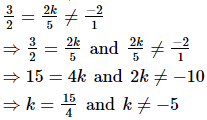
Hence, k =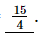

|
Explore Courses for Class 10 exam
|

|
















