Chapter 2 - Polynomials, RD Sharma Solutions - (Part-8) | RD Sharma Solutions for Class 10 Mathematics PDF Download
Page No 2.63
Ques.1. Quadratic polynomials, whose zeroes are –4 and 3 are given by ________.
Ans. Quadratic polynomial with given zeroes is
x2 – (sum of zeroes)x + (product of zeroes)
= x2 − (−4+3)x + (−4 × 3)
= x2 − (−1)x + (−12)
= x2 + x − 12
Hence, Quadratic polynomials, whose zeroes are –4 and 3 are given by x2 + x – 12.
Ques.2. Quadratic polynomials with rational coefficients having √3 as a zero are given by ________.
Ans. Irrational zeroes of a quadratic polynomial always occurs in pairs.
If one zero is √3 then, other zero is –√3.
Now,
Quadratic polynomial with given zeroes is
x2 – (sum of zeroes)x + (product of zeroes)
= x2−(√3–+(−√3))x + (√3× − √3)
= x2−(√3 − √3)x + (−3)
= x2 − 3
Hence, Quadratic polynomials with rational coefficients having √3 as a zero are given by x2 – 3.
Ques.3. The number of quadratic polynomials whose zeroes are 2 and – 3, is __________.
Ans. Quadratic polynomial with given zeroes is
x2 – (sum of zeroes)x + (product of zeroes)
=x2 − (−3 + 2)x + (−3 × 2)
=x2 − (−1)x + (−6)
=x2 + x − 6
Hence, the number of quadratic polynomials whose zeroes are 2 and – 3, is one.
Ques.4. The zeroes of the quadratic polynomial x2 + x – 6 are __________.
Ans. Let f(x) = x2 + x – 6
⇒ f(x) = x2 + x − 6
= x2 + 3x − 2x − 6
= x(x + 3) − 2(x + 3)
= (x − 2)(x + 3)
To find the zeroes, we put f(x) = 0
⇒ (x − 2)(x + 3)
⇒ (x − 2) = 0 or (x + 3) = 0
⇒ x = 2, −3
Hence, the zeroes of the quadratic polynomial x2 + x – 6 are 2 and –3.
Ques.5. The quadratic polynomials, the sum and product of whose zeroes are 7 and 12 are given by _________.
Ans. Quadratic polynomial with given zeroes is
x2 – (sum of zeroes)x + (product of zeroes)
= x2 − (7)x + (12)
= x2 − 7x + 12
Hence, quadratic polynomials, the sum and product of whose zeroes are 7 and 12 are given by x2 – 7x + 12.
Ques.6. If x + 1 is a factor of the polynomial 2x3 + ax2 + 4x + 1, then a = _________.
Ans. Let f(x) = 2x3 + ax2 + 4x + 1
It is given that one factor of f(x) is (x + 1).
Therefore, f(x) = 0 when x = −1.
On putting x = –1 in f(x) = 0, we get
2(−1)3 + a(−1)2 + 4(−1) + 1 = 0
⇒ 2(−1) + a(+1) + 4(−1) + 1 = 0
⇒ −2 + a − 4 + 1 = 0
⇒ a − 5 = 0
⇒ a = 5
Hence, a = 5.
Ques.7. If a + b + c = 0, then a zero of the polynomial ax2 + bx + c, is _________.
Ans. Let f(x) = ax2 + bx + c
It is given that a + b + c = 0
Therefore, when x = 1, f(x) = a(1)2 + b(1) + c = a + b + c = 0
Thus, x = 1 is the zero of f(x).
Hence, if a + b + c = 0, then a zero of the polynomial ax2 + bx + c, is 1.
Ques.8. If a + c = b, then a zero of the polynomial ax2 + bx + c, is _________.
Ans. Let f(x) = ax2 + bx + c
It is given that a + c = b
⇒ a − b + c = 0
Therefore, when x = −1, f(x) = a(−1)2 + b(−1) + c = a − b + c = 0
Thus, x = −1 is the zero of f(x).
Hence, if a + c = b, then a zero of the polynomial ax2 + bx + c, is −1.
Ques.9. The graph of a quadratic polynomial intersects the x-axis at the most at ________ points.
Ans. A quadratic polynomial has at most 2 zeroes.
Thus, it can intersects the x-axis at the most at 2 points.
Hence, the graph of a quadratic polynomial intersects the x-axis at the most at two points.
Ques.10. If two of the zeroes of a cubic polynomial are zero, then it does not have ______ and _______ terms.
Ans. Let f(x) = ax3 + bx2 + cx + d be a cubic polynomial.
Since, two of the zeroes of a cubic polynomial are zero, then the equation will be ax3 + bx2 = 0
Therefore, it does not have the linear term and the constant term.
Hence, If two of the zeroes of a cubic polynomial are zero, then it does not have linear and constant terms.
Ques.11. If all the zeroes of cubic polynomial x3 + ax2 – bx + c are negative then a, b and c all have _______ sign.
Ans. Let f(x) = x3 + ax2 – bx + c
Let the zeroes of f(x) be α, β, γ, where all these zeroes are negative
Then,
α + β + γ = −a
Thus, a is positive (∵ α, β, γ are negative)
αβ + βγ + γα = −b
Thus, b is positive (∵ α, β, γ are negative)
αβγ = −c
Thus, c is positive (∵ α, β, γ are negative)
Hence, if all the zeroes of cubic polynomial x3 + ax2 – bx + c are negative then a, b and c all have positive sign.
Ques.12. If the zeroes of the quadratic polynomial ax2 + x + a are equal, then a = ________.
Ans. Let f(x) = ax2 + x + a
Let the zeroes of f(x) be α and α. (∵the zeroes are equal)
Then,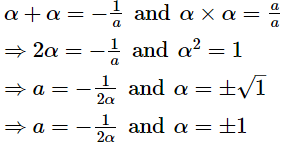
For α = 1, a = -(1/2)
For α=-1, a= (1/2)
Hence, if the zeroes of the quadratic polynomial ax2 + x + a are equal, then a =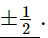
Ques.13. If the zeroes of the quadratic polynomial ax2 + bx + c are both negative, then a, b and c all have the _______ sign.
Ans. Let f(x) = ax2 + bx + c
Let the zeroes of f(x) be α, β, where all these zeroes are negative.
Then,
α+ β = -(b/a)
∵ α, β are negative
∴ b/a is positive
⇒ either both a and b are positive or both are negative.
αβ = c/a
∵ α, β are negative
∴ c/a is positive
⇒ either both a and c are positive or both are negative.
Hence, if the zeroes of the quadratic polynomial ax2 + bx + c are both negative, then a, b and c all have the same sign.
Ques.14. If x + α is a factor of the polynomial 2x2 + 2αx + 4x + 12, then α = _______.
Ans. Let f(x) = 2x2 + 2αx + 4x + 12
It is given that one factor of f(x) is (x + α).
Therefore, f(x) = 0 when x = −α.
On putting x = –α in f(x) = 0, we get
2(−α)2 + 2α(−α) + 4(−α) + 12 = 0
⇒2(α)2 − 2α2 − 4α + 12 = 0
⇒ −4α + 12 = 0
⇒ −4α = −12
⇒ α = 3
Hence, if x + α is a factor of the polynomial 2x2 + 2αx + 4x + 12, then α = 3.
Ques.15. If –4 is a zero of the polynomial x2 – x – (2k + 2), then k = _________.
Ans. Let f(x) = x2 – x – (2k + 2)
It is given that –4 is a zero of f(x).
Therefore, f(x) = 0 when x = −4.
On putting x = –4 in f(x) = 0, we get
(−4)2 − (−4) − (2k + 2) = 0
⇒ 16 + 4 − 2k − 2 = 0
⇒ 20 − 2k − 2 = 0
⇒ 18 − 2k = 0
⇒ 2k = 18
⇒ k = 9
Hence, if –4 is a zero of the polynomial x2 – x – (2k + 2), then k = 9.
Ques.16. If 4x2 – 6x – m is divisible by x – 3, then m = ________.
Ans. Let f(x) = 4x2 – 6x – m
It is given that f(x) is divisible by x – 3.
Therefore, f(x) = 0 when x = 3.
On putting x = 3 in f(x) = 0, we get
4(3)2 − 6(3) − m = 0
⇒ 4(9) − 6(3)−m = 0
⇒ 36 − 18 − m = 0
⇒ 18 − m = 0
⇒ m = 18
Hence, if 4x2 – 6x – m is divisible by x – 3, then m = 18.
Ques.17. If a, a + b, a + 2b are zeroes of the cubic polynomial x3 – 6x2 + 3x + 10, then a + b = ________.
Ans. Let f(x) = x3 – 6x2 + 3x + 10
Let the zeroes of f(x) be a, a + b, a + 2b.
Then,
Sum of zeroes = 6
⇒ a + (a + b) + (a + 2b) = 6
⇒ 3a + 3b = 6
⇒ 3(a + b) = 6
⇒ a + b = 2
Hence, if a, a + b, a + 2b are zeroes of the cubic polynomial x3 – 6x2 + 3x + 10, then a + b = 2.
Ques.18. If one zero of the quadratic polynomial 2x2 – 6kx + 6x – 7 is negative of the other, then k = ________.
Ans. Let f(x) = 2x2 – 6kx + 6x – 7 = 2x2 + (– 6k + 6)x – 7
Let the zeroes of f(x) be α and −α. (∵ one zero is negative of the other)
Then,
(α) + (−α) = 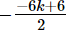
⇒ α − α = −(−3k + 3)
⇒ 0 = 3k − 3
⇒ 3k = 3
⇒ k = 1
Hence, if one zero of the quadratic polynomial 2x2 – 6kx + 6x – 7 is negative of the other, then k = 1.
Ques.19. If the product of the zeroes of the quadratic polynomial x2 – 3ax + 2a2 – 1 is 7, then a = _______.
Ans. Let f(x) = x2 – 3ax + 2a2 – 1
Let the zeroes of f(x) be α and β.
Then,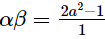
⇒ αβ = 2a2 − 1
⇒ 2a2 − 1 = 7 (∵ product of zeroes is 7)
⇒ 2a2 = 8
⇒ a2 = 4
⇒ a = ±2
Hence, if the product of the zeroes of the quadratic polynomial x2 – 3ax + 2a2 – 1 is 7, then a = ±2.
Ques.20. The sum of the zeros of the quadratic polynomial 2x2 – 3k is ________.
Ans. Let f(x) = 2x2 – 3k = 2x2 + 0x – 3k
Let the zeroes of f(x) be α and β.
Then,
α + β = − (0/2)
⇒ α + β = 0
Hence, the sum of the zeroes of the quadratic polynomial 2x2 – 3k is 0.
Ques.21. The parabola representing a quadratic polynomial f(x) = ax2 + bx + c opens upward when _________.
Ans. Let f(x) = ax2 + bx + c
When a > 0, the parabola representing f(x) opens upward.
When a < 0, the parabola representing f(x) opens downward.
Hence, the parabola representing a quadratic polynomial f(x) = ax2 + bx + c opens upward when a is positive.
Ques.22. The parabola representing a quadratic polynomial f(x) = ax2 + bx + c opens downward when __________.
Ans. Let f(x) = ax2 + bx + c
When a > 0, the parabola representing f(x) opens upward.
When a < 0, the parabola representing f(x) opens downward.
Hence, the parabola representing a quadratic polynomial f(x) = ax2 + bx + c opens downward when a is negative.
Ques.23. If the parabola represented by f(x) = ax2 + bx + c cuts x-axis at two distinct points, then the polynomial ax2 + bx + c has ________ real zeroes.
Ans. Let f(x) = ax2 + bx + c
If f(x) has two real and distinct zeroes, the parabola represented by f(x) cuts x-axis at two distinct points.
If f(x) has two real and equal zeroes, the parabola represented by f(x) touches x-axis at only one distinct point.
Hence, if the parabola represented by f(x) = ax2 + bx + c cuts x-axis at two distinct points, then the polynomial ax2 + bx + c has 2 real zeroes.
Ques.24. The maximum number of zeroes which a quadratic polynomial can have is _________.
Ans. Let f(x) = ax2 + bx + c
Maximum number of zeroes of polynomial = Highest power of x = 2
Therefore, It has at most 2 zeroes.
Hence, the maximum number of zeroes which a quadratic polynomial can have is 2.
Page No 2.64
Ques.1. Define a polynomial with real coefficients.
Ans. In the polynomial f(x) = anxn + an - 1xn - 1 + .... + a1x + a0,
anxn, an-1xn-1, ...,a1x, and a0 are known as the terms of the polynomial and an, an-1,...,a1 and a0 are their real coefficients.
For example, p(x) = 3x - 2 is a polynomial and 3 is a real coefficient
Ques.2. Define degree of a polynomial.
Ans. The exponent of the highest degree term in a polynomial is known as its degree.
In other words, the highest power of x in a polynomial f(x) is called the degree of the polynomial f(x).
For Example: g(x) = 2x2 + 3x + 4 is a polynomial in the variable x of degree 2.
Ques.3. Write the standard form of a linear polynomial with real coefficients.
Ans. Any linear polynomial in variable x with real coefficients is of the form f(x) = ax + b, where a, b are real numbers and a ≠ 0.
Ques.4. Write the standard form of a quadratic polynomial with real coefficients.
Ans. Any quadratic polynomial in variable x with real coefficients is of the form f(x) = ax2 + bx + c, where a, b, c are real numbers and a ≠ 0.
Ques.5. Write the standard form of a cubic polynomial with real coefficients.
Ans. The most general form of a cubic polynomial with coefficients as real numbers is of the form f(x) = ax3 + bx2 + cx + d, where a, b, c, d are real number and a ≠ 0.
FAQs on Chapter 2 - Polynomials, RD Sharma Solutions - (Part-8) - RD Sharma Solutions for Class 10 Mathematics
| 1. What are the different types of polynomials? |  |
| 2. How can we determine the degree of a polynomial? |  |
| 3. What is the difference between a constant and a variable in a polynomial? |  |
| 4. Can a polynomial have negative exponents? |  |
| 5. How can we add or subtract polynomials? |  |

|
Explore Courses for Class 10 exam
|

|

















