Chapter 2 - Polynomials, RD Sharma Solutions - (Part-9) | RD Sharma Solutions for Class 10 Mathematics PDF Download
Page No 2.64
Ques.6. Define value of polynomial at a point.
Ans. If f(x) is a polynomial and α is any real number, then the real number obtained by replacing x by α in f(x), is called the value of f(x) at x = α and is denoted by f(α).
Ques.7. Define the zero of a polynomial.
Ans. The zero of a polynomial f(x) is defined as any real number α such that f(α) = 0.
Ques.8. The sum and product of the zeros of a quadratic polynomial are −1/2 and −3 respectively. What is the quadratic polynomial.
Ans. Let sum of quadratic polynomial is α + β = (-1)/2
Product of the quadratic polynomial is αβ = -3
Let S and P denote the sum and product of the zeros of a polynomial as (-1)/2 and -3.
Then
The required polynomial g(x) is given by 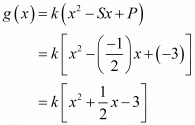
Hence, the quadratic polynomial is  , where k is any non-zero real number.
, where k is any non-zero real number.
Ques.9. Write the family of quadratic polynomials having −(1/4) and 1 as its zeros.
Ans. We know that, if x = α is a zero of a polynomial then x - 2 is a factor of quadratic polynomials.
Since (-1)/4 and 1 are zeros of polynomial.
Therefore 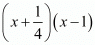
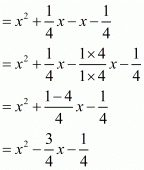
Hence, the family of quadratic polynomials is  , where k is any non-zero real number.
, where k is any non-zero real number.
Ques.10. If the product of zeros of the quadratic polynomial f(x) = x2 − 4x + k is 3, find the value of k.
Ans. We have to find the value of k.
Given,
The product of the zeros of the quadratic polynomial f(x) = x2 - 4x + k is 3
Product of the polynomial = 3
Constant term/Coefficient of x3 = 3
k/1 = 3
k = 3 x 1
k = 3
Hence, the value of k is k = 3.
Ques.11. If the sum of the zeros of the quadratic polynomial f(x) = kx2 − 3x + 5 is 1, write the value of k.
Ans. We have to find the value of k, if the sum of the zeros of the quadratic polynomial f(x) = kx2 - 3x + 5 is 1.
Given
Sum of the polynomial = 1
(-Coefficient of x)/(Coefficient of x2)= 1
-((-3)/k) = 1
3 = 1 x k
3 = k
Hence, the value of k is 3.
Ques.12. In the graph of a polynomial p(x) is given. Find the zeros of the polynomial.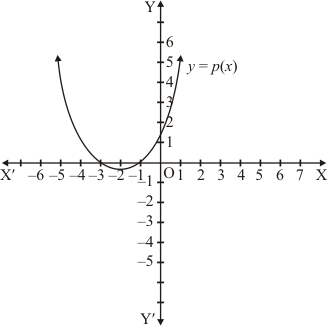
Ans. Just see the point of intersection of the curve and x-axis and find out the x-coordinate of these points. These x-coordinates will be the zeros of the polynomial.
Since the intersection points are (-3, 0) and (-1, 0)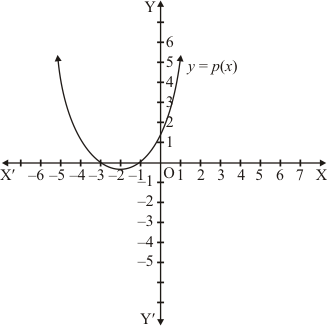
Hence, the zeros of the polynomial is -3 and -1.
Ques.13. The graph of a polynomial y = f(x). Find the number of real zeros of f(x).
Ans. A real number α is a zero of polynomial f(x), if f(α) = 0.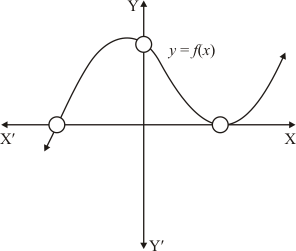
In the above figure the curve intersects x-axis at one point and touches at one point
When a curve touches x-axis at one point, it means it has two common zeros at that point
Hence the number of real zeroes is 3.
Page No 2.65
Ques.14. The graph of the polynomial f(x) = ax2 + bx + c is as shown below. Write the signs of 'a' and b2 − 4ac.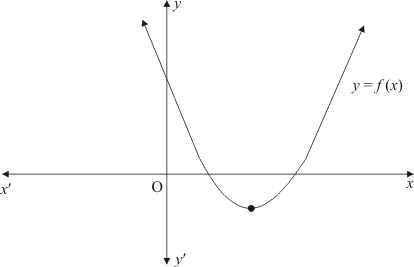
Ans. 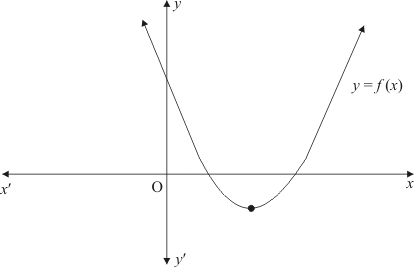
Clearly, f(x) = ax2 + bx + c represent a parabola opening upwards. Therefore, a > 0
Since the parabola cuts x-axis at two points, this means that the polynomial will have two real solutions
Hence b2 - 4ac > 0
Hence a > 0 and b2 - 4ac > 0.
Ques.15. The graph of the polynomial f(x) = ax2 + bx + c is as shown in Fig. Write the value of b2 − 4ac and the number of real zeros of f(x).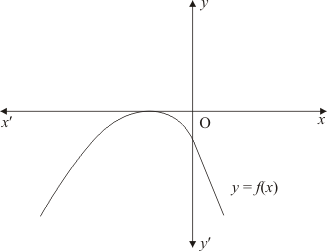
Ans. The graph of the polynomial f(x) = ax2 + bx + c or the curve touches x−axis at point (((-b)/2a), 0). The x-coordinate of this point gives two equal zeros of the polynomial and b2 - 4ac = 0.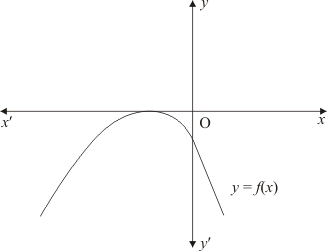
Hence the number of real zeros of f(x) is 2 and b2 - 4ac = 0.
Ques.16. In Q. No. 14, write the sign of c.
Ans. The parabola y = ax2+ bx + c cuts y-axis at point P which lies on y-axis. Putting x = 0 in y = ax2 + bx +c, we get y = c. So the coordinates of P are (0, c). Clearly, P lies on OY. Therefore c > 0 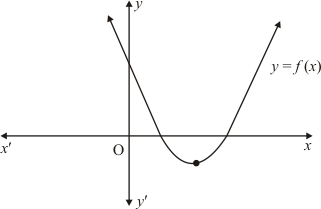
Hence, the sign of c is c > 0.
Ques.17. In Q. No. 15, write the sign of c.
Ans. The parabola y = ax2 + bx + c cuts y-axis at P which lies on OY.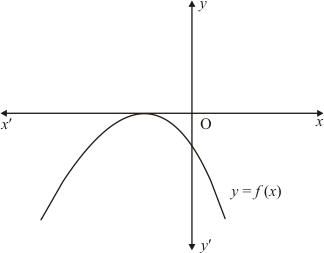
Putting x =0 in y = ax2 + bx + c, we get y=c. So the coordinates of P are (0, c). Clearly, P lies on OY. Therefore c < 0.
Ques.18. The graph of a polynomial f(x) is as shown in Fig. Write the number of real zeros of f(x).
Ans. The graph of a polynomial f(x) touches x−axis at two points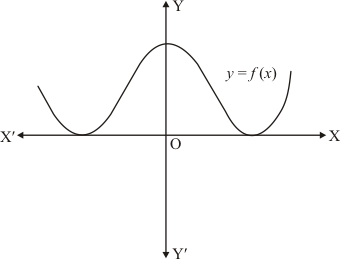
We know that if a curve touches the x-axis at two points then it has two common zeros of f(x).
Hence the number of zeros of f(x), in this case is 2.
Ques.19. If x = 1 is a zero of the polynomial f(x) = x3 − 2x2 + 4x + k, write the value of k.
Ans. We have to find the value of K if x = 1 is a zero of the polynomial f(x) = x3 − 2x2 + 4x + k.
f(x) = x3 - 2x2 + 4x + k
f(1) = 13 - 2(1)2 + 4 x 1 + k
0 = 1 - 2 + 4 + k
0 = 5 - 2 + k
0 = 3 + k
-3 = k
Hence, the value of k is k = -3.
Ques.20. State division algorithm for polynomials.
Ans. If f(x) and g(x) are any two polynomials with g(x) ≠ 0, then we can always find polynomials q(x) and r(x) such that f(x) = q(x)g(x) + r(x), where r(x) = 0 or degree r(x) < degree g(x).
Ques.21. Give an example of polynomials f(x), g(x), q(x) and r(x) satisfying f(x) = g(x), q(x) + r(x), where degree r(x) = 0.
Ans. Using division algorithm, we have
f(x) = g(x) x q(x) + r(x)
Hence an example for polynomial f(x),g(x), q(x) and r(x) satisfying f(x) = g(x) x q(x) + r(x) are
f(x) = x5 - 4x3 + x2 + 3x + 1
g(x) = (x3 - 3x + 1)
q(x) = (x2 - 1)
r(x) = 2
Ques.22. Write a quadratic polynomial, sum of whose zeros is 2√3 and their product is 2.
Ans. Let S and P denotes respectively the sum and product of the zeros of a polynomial are 2√3 and 2.
The required polynomial g(x) is given by
g(x) = k(x2 - Sx + P)
g(x) = k(x2 - 2√3x + 2)
Hence, the quadratic polynomial is g(x) = k(x2 - 2√3x + 2) where k is any non-zeros real number.
Ques.23. If fourth degree polynomial is divided by a quadratic polynomial, write the degree of the remainder.
Ans. Here f(x) represent dividend and g(x) represent divisor.
g(x) = quadratic polynomial
g(x) = ax2 + bx + c
Therefore degree of (f(x)) = 4
Degree of (g(x)) = 2
The quotient q(x) is of degree 2(= 4 - 2)
The remainder r(x) is of degree 1 or less.
Hence, the degree of the remainder is equal to 1 or less than 1.
Ques.24. If f(x) = x3 + x2 − ax + b is divisible by x2 − x write the value of a and b.
Ans. We are given f(x) = x3 + x2 − ax + b is exactly divisible by x2 - x then the remainder should be zero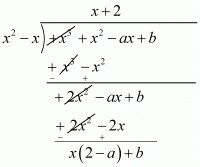
Therefore Quotient = x + 2 and
Remainder = x(2 - a) + b
Now, Remainder = 0
x(2 - a) + b = 0
x(2 - a) + b = 0x + 0
Equating coefficient of x, we get
2 - a = 0
2 = a
Equating constant term
b = 0
Hence, the value of a and b are a = 2, b = 0.
Ques.25. If a − b, a and b are zeros of the polynomial f(x) = 2x3 − 6x2 + 5x − 7, write the value of a.
Ans. Let a − b, a and a + b be the zeros of the polynomial f(x) = 2x3 − 6x2 + 5x − 7 then
Sum of the zeros = ((-Coefficient of x2)/Coefficient of x3)
(a - d) + a + (a + d) = -((-6)/2)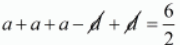
3a = 3
a = 3/3
a = 1
Hence, the value of a is 1.
Page No 2.66
Ques.26. Write the coefficient of the polynomial p(z) = z5 − 2z2 + 4.
Ans. We have to find the co-efficient of the polynomial p(z) = z5 − 2z2 + 4.
Co-efficient of z5 = 1
Co-efficient of z4 = 0
Co-efficient of z3 = 0
Co-efficient of z2 = -2
Co-efficient of z = 0
Constant term = 4
Hence, the co-efficient of z5, z4, z3, z2, z and constant term is 1, 0, 0, -2, 0, 4.
Ques.27. Write the zeros of the polynomial x2 − x − 6.
Ans. We have to find the zeros of the polynomial x2 − x − 6.
f(x) = x2 - x - 6
f(x) = x2 - 3x + 2x - 6
f(x) = x(x - 3) + 2(x - 3)
f(x) = (x + 2)(x - 3)
We know that if (x - α) is a factor of f(x) then x = α is a zero of polynomial
Therefore we have
x + 2 = 0
x = -2
Also,
x - 3 = 0
x = 3
Hence, the zeros of polynomial x2 - x - 6 is 3, -2.
Ques.28. If (x + a) is a factor of 2x2 + 2ax + 5x + 10, find a.
Ans. Given (x + a) is a factor of f(x) = 2x2 + 2ax + 5x + 10.
Let us now divide f(x) by x + a.
We have,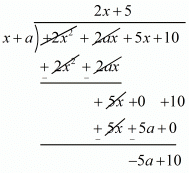
Now, remainder = 0
10 - 5a = 0
10 = 5a
10/5 = a
2 = a
Hence, the value of a is 2.
Ques.29. For what value of k, −4 is a zero of the polynomial x2 − x − (2k + 2)?
Ans. We know that if x = α is zero polynomial then x - 2 is a factor of f(x).
Since -4 is zero of f(x)
Therefore x + 4 is a factor of f(x)
Now, we divide f(x) = x2 - x - (2k + 2) by g(x) = x + 4 to find the value of k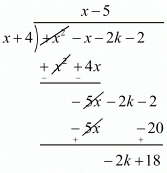
Now, Remainder = 0
-2k + 18 = 0
-2k = -18
k = (18/2)
k = 9
Hence, the value of k is 9.
Ques.30. If 1 is a zero of the polynomial p(x) = ax2 − 3(a − 1) x − 1, then find the value of a.
Ans. We know that if x = α is a zero of polynomial then x - α is a factor of p(x)
Since 1 is zero of p(x)
Therefore, x - 1 is a factor of p(x)
Now, we divide p(x) = ax2 - 3(a - 1)x - 1by x − 1.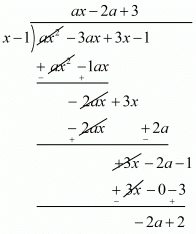
Now, Remainder = 0
-2a + 2 = 0
-2a = -2
a = 2/2
a = 1
Hence, the value of a is 1.
Ques.31. If α, β are the zeros of a polynomial such that α + β = −6 and αβ = −4, then write the polynomial.
Ans. Let S and P denotes respectively the sum and product of the zeros of a polynomial
We are given S = -6 and P = -4. Then
The required polynomial g(x) is given by
g(x) = x2 -(-6)x + (-4)
= x2 + 6x - 4
Hence, the polynomial is x2 + 6x - 4.
Ques.32. If α, β are the zeros of the polynomial 2y2 + 7y + 5, write the value of α + β + αβ.
Ans. Let α and β are the zeros of the polynomial f(x) = 2y2 + 7y + 5. Then
The sum of the zeros = ((-Coefficient of y)/Coefficient of y2) = ((-7)/2). The product of the zeros = Constant term/Coefficient of y2 = 5/2
Then the value of α + β + αβ is
α + β + αβ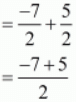
= (-2)/2
= -1
Hence, the value of α + β + αβ is -1.
Ques.33. For what value of k, is 3 a zero of the polynomial 2x2 + x + k?
Ans. We know that if x = α is zero polynomial, and then x - α is a factor of f(x).
Since 3 is zero of f(x)
Therefore x -3 is a factor of f(x)
Now, we divide f(x) = 2x2 + x + k by g(x) = x - 3 to find the value of k
Now, remainder = 0
k + 21 = 0
k = -21
Hence, the value of k is -21.
Ques.34. For what value of k, is −3 a zero of the polynomial x2 + 11x + k?
Ans. We know that if x = α is zeros polynomial, then x - α is a factor of f(x)
Since -3 is zero of f(x). Therefore x + 3 is a factor of f(x)
Now, we divide f(x) = x2 + 11x + k by g(x) = x + 3 to find the value of k.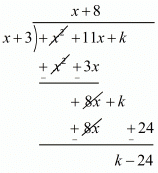
Now, Remainder = 0
k - 24 = 0
k = 24
Hence, the value of k is 24.
Ques.35. For what value of k, is −2 a zero of the polynomial 3x2 + 4x + 2k?
Ans. We know that if x = α is zero polynomial then x - α is a factor of f(x)
Since -2 is a factor of f(x).Therefore x + 2 is a factor of f(x)
Now, we divide f(x) = 3x2 + 4x + 2k by g(x) = x + 2 to find the value of k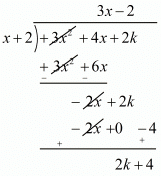
Now, Remainder = 0
2k + 4 = 0
2k = -4
k = -4/2
k = -2
Hence, the value of k is -2.
Ques.36. If a quadratic polynomial f(x) is factorizable into linear distinct factors, then what is the total number of real and distinct zeros of f(x)?
Ans. If a quadratic polynomial f(x) = ax2 + bx + c is factorized into linear polynomials then the total number of real and distinct zeros of f(x) will be 2.
Ques.37. If a quadratic polynomial f(x) is a square of a linear polynomial, then its two zeros are coincident. (True/False).
Ans. The polynomial f(x) = x2 = (x - 0)(x - 0) has two identical factors. The curve y = x2 cuts X axis at two coincident points that is exactly at one point.
Hence, quadratic polynomial f(x) is a square of linear polynomial then its two zeros are coincident. True
Ques.38. If a quadratic polynomial f(x) is not factorizable into linear factors, then it has no real zero. (True/False)
Ans. When polynomial f(x) = ax2 + bx + c is not factorizable then the curve y = ax2 + bx + c does not touch x-axis. Parabola open upwards above the x-axis or open downwards below x-axis where a > 0 or a < 0.
Hence, if quadratic polynomial f(x) is not factorizable into linear factors then it has no real zeros. True.
Ques.39. If f(x) is a polynomial such that f(a) f(b) < 0, then what is the number of zeros lying between a and b?
Ans. If f(x) is a polynomial such that f(a)f(b) < 0 then this means the value of the polynomial are of different sign for a to b
Hence, at least one zero will be lying between a and b
Ques.40. If graph of quadratic polynomial ax2 + bx + c cuts positive direction of y-axis, then what is the sign of c?
Ans. If graph of quadratic polynomial f(x) = ax2 + bx + x cuts positive direction of y−axis, then
Put x = 0 for the point of intersection of the polynomial and y−axis
We have y = 0 + 0 + c = c
Since the point (0, c) is above the x-axis
Hence, the sign of c is positive, that is c > 0.
Ques.41. If the graph of quadratic polynomial ax2 + bx + c cuts negative direction of y-axis, then what is the sign of c?
Ans. Since graph of quadratic polynomial f(x) = ax2 + bx + c cuts negative direction of y−axis
So put x=0 to find the intersection point on y-axis
y = 0 + 0 + c = c
So the point is (0 , c)
Now it is given that the quadratic polynomial cuts negative direction of y
So c < 0
FAQs on Chapter 2 - Polynomials, RD Sharma Solutions - (Part-9) - RD Sharma Solutions for Class 10 Mathematics
| 1. What are polynomials? |  |
| 2. How do you determine the degree of a polynomial? |  |
| 3. What is the standard form of a polynomial? |  |
| 4. How do you add or subtract polynomials? |  |
| 5. How do you multiply polynomials? |  |

|
Explore Courses for Class 10 exam
|

|

















