Chapter 5 - Quadratic Equations, RD Sharma Solutions - (Part-1) | RD Sharma Solutions for Class 10 Mathematics PDF Download

Page No 5.11

Ques.1. For the following arithmetic progressions write the first term a and the common difference d:
(i) −5, −1, 3, 7, ...
(ii) 1/5, 3/5, 5/5, 7/5
(iii) 0.3, 0.55, 0.80, 1.05, ...
(iv) −1.1, −3.1, −5.1, −7.1, ...
Ans. In the given problem, we need to write the first term (a) and the common difference (d) of the given A.P
(i) −5, −1, 3, 7 …
Here, first term of the given A.P is (a) = −5
Now, we will find the difference between the two terms of the given A.P
a₂ - a₁ = -1 - (-5)
a₂ - a₁ = 4
Similarly,
a₃ - a₂ = 3-(-1)
a₃ - a₂ = 4
Also,
a₄ - a₃ = 7 - 3
a₄ - a₃ = 4
As a₂ - a₁ = a₃ - a₂ = a₄ - a₃ = 4
Therefore, the first term of the given A.P is a = -5 and the common difference of the given is d = 4.
(ii) 1/5, 3/5, 5/5, 7/5, .....
Here, first term of the given A.P is (a) = 1/5
Now, we will find the difference between the two terms of the given A.P
a₂ - a₁ = (3/5)-(1/5)
a₂ - a₁ = 2/5
Similarly,
a₃ - a₂ = 5/5 - 3/5
a₃ - a₂ = 2/5
Also,
a₄ - a₃ = 7/5 - 5/5
a₄ - a₃ = 2/5
As a₂ - a₁ = a₃ - a₂ = a₄ - a₃ = 2/5
Therefore, the first term of the given A.P is a = 1/5 and the common difference is d = 2/5.
(iii) 0.3, 0.55, 0.80, 1.05, …
Here, first term of the given A.P is (a) = 0.3
Now, we will find the difference between the two terms of the given A.P
a₂ - a₁ = 0.55 - 0.3
a₂ - a₁ = 0.25
Similarly,
a₃ - a₂ = 0.80 - 0.55
a₃ - a₂ = 0.25
Also,
a₄ - a₃ = 1.05 - 0.80
a₄ - a₃ = 0.25
As a₂ - a₁ = a₃ - a₂ = a₄ - a₃ = 0.25
Therefore, the first term of A.P is a = 0.3 and the common difference is d = 0.25.
(iv) −1.1, −3.1, −5.1, −7.1...
Here, first term of the given A.P is (a) = −1.1
Now, we will find the difference between the two terms of the given A.P
a₂ - a₁ = -3.1-(-1.1)
a₂ - a₁ = -2
Similarly,
a₃ - a₂ = -5.1-(-3.1)
a₃ - a₂ = -2
Also,
a₄ - a₃ = -7.1-(-5.1)
a₄ - a₃ = -2
As a₂ - a₁ = a₃ - a₂ = a₄ - a₃ = -2
Therefore, the first term of A.P is a = -1.1 and the common difference is d = -2.

Ques.2. Write the arithmetic progression when first term a and common difference d are as follows:
(i) a = 4, d = −3
(ii) a = −1, d = 1/2
(iii) a = −1.5, d = −0.5
Ans. In the given problem, we are given its first term (a) and common difference (d).
We need to find the A.P
(i) a = 4, d = -3
Now, as a = 4
A.P would be represented by a, a₁, a₂, a₃, a₄,...
So,
a₁ = a + d
a₁ = 4 + (-3)
a₁ = 1
Similarly,
a₂ = a₁ + d
a₂ = 1 + (-3)
a₂ = -2
Also,
a₃ = a₂ + d
a₃ = -2 + (-3)
a₃ = -5
Further,
a₄ = a₃ + d
a₄ = -5 + (-3)
a₄ = -8
Therefore, A.P with a = 4 and d = -3 is 4, 1, -2, -5, -8, ....
(ii) a = -1, d = 1/2
Now, as a = -2
A.P would be represented by a, a₁, a₂, a₃, a₄,...
So,
a₁ = a + d
a₁ = -1 + (1/2)
a₁ =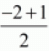
a₁ = (-1)/2
Similarly,
a₂ = a₁ + d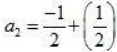

a₂ = 0
Also,
a₃  = a₂ + d
a₃ = 0 + (1/2)
a₃ = 1/2
Further,
a₄ = a₃ + d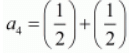

a₄ = 2/2
a₄ = 1
Therefore, A.P with a = 4 and d = -3 is
(iii) a = -1.5, d = -0.5
Now, as a = -1.5
A.P would be represented by a, a₁, a₂, a₃, a₄,...
So,
a₁ = a + d
a₁ = -1.5 + (0.5)
a₁ = -2
Similarly,
a₂ = a₁ + d
a₂ = -2 + (-0.5)
a₂ = -2.5
Also,
a₃ = a₂ + d
a₃  = -2.5 + (-0.5)
a₃ = -3
Further,
a₄ = a₃ + d
a₄ = -3 + (-0.5)
a₄ = -3.5
Therefore, A.P with a = 4 and d = -3 is -1.5, -2, -2.5, -3, -3.5, ....

Ques.3. In which of the following situations, the sequence of numbers formed will form an A.P.?
(i) The cost of digging a well for the first metre is Rs 150 and rises by Rs 20 for each succeeding metre.
(ii) The amount of air present in the cylinder when a vacuum pump removes each time 1/4 of their remaining in the cylinder.
Ans. (i) In the given problem,
Cost of digging a well for the first meter = Rs 150
Cost of digging a well for subsequent meter is increased by Rs 20
So,
Cost of digging a well of depth one meter = Rs. 150
Cost of digging a well of depth two meters= Rs 150 + 20 = Rs. 170
Cost of digging a well of depth three meters= Rs 150 + 20 + 20 = Rs. 190
Cost of digging a well of depth four meters = Rs 150 + 20 + 20 +20 = Rs. 210
Thus, the costs of digging a well of different depths are 150, 170, 190, 210,...
Now, for a sequence to be an A.P., the difference between adjacent terms should be equal.
Here,
a₁ - a = 170 - 150 = 20
Also,
a₂ - a₁ = 190 - 170 = 20
Therefore, a₁ - a = a₂ - a₁
Since the terms of the sequence are at a common difference of 20, the above sequence is an A.P. with the first term as a = 150 and common difference d = 20.
(ii) Here, let us take the initial amount of air present in the cylinder as 100 units.
So,
Amount left after vacuum pump removes air for 1^st time = 100-(1/4)100
= 100 - 25
= 75
Amount left after vacuum pump removes air for 2^nd time = 75 - (1/4)75
= 75 - 18.75
= 56.25
Amount left after vacuum pump removes air for 3^rd time = 56.25 - (1/4)56.25
= 56.25 - 14.06
= 42.19
Thus, the amount left in the cylinder at various stages is 100, 75, 56, 25, 42, 19,...
Now, for a sequence to be an A.P., the difference between adjacent terms should be equal.
Here,
a₁ - a = 75 - 100 = -25
Also,
a₂ - a₁ = 56.25 - 75
= -18.75
Since, a₁ - a ≠ a₂ - a₁
The sequence is not an A.P.

Ques.4. Find the common difference and write the next four terms of each of the following arithmetic progressions:
(i) 1, −2, −5, −8, ...
(ii) 0, −3, −6, −9, ...
(iii) -1, 1/4, 3/2, ...
(iv) -1, 5/6, 2/3, ...
Ans. In the given problem, we need to find the common difference and the next four terms of the given A.P.
(i) 1, −2, −5, −8, ...
Here, first term (a₁) = 1
Common difference (d) = a₂ - a₁
= -2 - 1
= -3
Now, we need to find the next four terms of the given A.P
That is we need to find a₅,a_6,a₇,a₈.
So, using the formula a_n = a + (n - 1)d
Substituting n = 5, 6, 7, 8 in the above formula
Substituting n = 5, we get
a₅ = 1 + (5 - 1)(-3)
a₅ = 1 - 12
a₅ = -11
Substituting n = 6, we get
a₆ = 1 + (6 - 1)(-3)
a₆ = 1 - 15
a₆ = -14
Substituting n = 7, we get
a₇ = 1 + (7 - 1)(-3)
a₇ = 1 - 18
a₇ = -17
Substituting n = 8, we get
a₈ = 1 + (8 - 1)(-3)
a₈ = 1 - 21
a₈ = -20
Therefore, the common difference is d = -3 and the next four terms are -11, -14, -17, -20.
(ii) 0, -3, -6, -9, ...
Here, first term (a₁) = 0
Common difference (d) = a₂ - a₁
= -3 - 0
= -3
Now, we need to find the next four terms of the given A.P
That is we need to find a₅,a_6,a₇,a_8,
So, using the formula a_n = a + (n - 1)d
Substituting n = 5, 6, 7, 8 in the above formula

Substituting n = 5, we get
a₅ = 0 + (5 - 1)(-3)
a₅ = 0 - 12
a₅ = -12
Substituting n = 6, we get
a₆ = 0 + (6 - 1)(-3)
a₆ = 0 - 15
a₆ = -15
Substituting n = 7, we get
a₇ = 0 + (7 - 1)(-3)
a₇ = 0 - 18
a₇ = -18
Substituting n = 8, we get
a₈ = 0 + (8 - 1)(-3)
a₈ = 0 - 21
a₈ = -21
Therefore, the common difference is d = -3 and the next four terms are -12, -15, -18, -21.
(iii) −1, 1/4, 3/2, ...
Here, first term (a₁) = −1
Common difference (d) = a₂ - a₁
= (1/4)-(-1)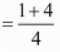

= 5/4
Now, we need to find the next four terms of the given A.P
That is we need to find a₄, a₅, a₆, a₇
So, using the formula a_n = a + (n - 1)d
Substituting n = 4, 5, 6, 7 in the above formula
Substituting n = 4, we get
a₄ = -1 + (4 - 1)(5/4)
a₄ = -1 + (15/4)
a₄ =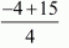
a₄ = 11/4
Substituting n = 5, we get
a₅ = -1 + (5 - 4)(5/4)
a₅ = -1 + 5
a₅ = 4
Substituting n = 6, we get
a₆ = -1 + (6 - 1)(5/4)
a₆ = -1 + (25/4)
a₆ =
a₆ = = 21/4
Substituting n = 7, we get
a₇ = -1 (7 - 1)(5/4)
a₇ = -1 + (30/4)
a₇ =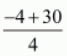
a₇ = 26/4
Therefore, the common difference is d = 5/4 and the next four terms are 11/4, 4, 21/4, 26/4.
(iv) -1, 5/6, 2/3, ...
Here, first term (a₁) = −1
Common difference (d) = a₂ - a₁
= -(5/6)-(-1)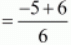

= 1/6
Now, we need to find the next four terms of the given A.P
That is we need to find a₄, a₅, a₆, a₇
So, using the formula a_n = a + (n - 1)d
Substituting n = 4, 5, 6, 7 in the above formula
Substituting n = 4, we get
a₄ = −1 + (4 − 1)(1/6)
a₄ = −1 + (1/2)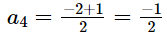

Substituting n = 5, we get
a₅ = -1 + (5 - 1)(1/6)
a₅ = -1 + (2/3)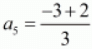

a₅ = - (1/3)
Substituting n = 6, we get
a₆ = -1 + (6 - 1)(1/6)
a₆ = -1 + (5/6)
a₆ =
a₆ = -(1/6)
Substituting n = 7, we get
a₇ = -1 + (7 - 1)(1/6)
a₇ = -1 + 1
a₇ = 0
Therefore, the common difference is d = 1/6 and the next four terms are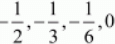

Ques.5. Which of the following sequences are arithmetic progressions. For those which are arithmetic progressions, find out the common difference.
(i) 3, 6, 12, 24, ...
(ii) 0, −4, −8, −12, ...
(iii) 1/2,1/4,1/6,1/8, ...
(iv) 12, 2, −8, −18, ...
(v) 3, 3, 3, 3, ...
(vi) p, p + 90, p + 180 p + 270, ... where p = (999)⁹⁹⁹
(vii) 1.0, 1.7, 2.4, 3.1, ...
(viii) −225, −425, −625, −825, ...
(ix) 10, 10 + 2⁵, 10 + 2⁶, 10 + 2⁷,...
(x) a + b, (a + 1) + b, (a + 1) + (b + 1), (a + 2) + (b + 1), (a + 2) + (b + 2), ...
(xi) 1², 3², 5², 7², ...
(xii) 1², 5², 7², 73, ...
Ans. In the given problem, we are given various sequences.
We need to find out that the given sequences are an A.P or not and then find its common difference (d)
(i) 3, 6, 12, 24, ...
Here,
First term (a) = 3
a₁ = 6
a₂ = 12
Now, for the given to sequence to be an A.P,
Common difference (d) = a₁ - a = a₂ - a₁
Here,
a₁ - a = 6 - 3
3
Also,
a₂ - a₁ = 12 - 6
= 6
Since a₁ - a ≠ a₂ - a₁
Hence, the given sequence is not an A.P.
(ii) 0, −4, −8, −12, ...
Here,
First term (a) = 0
a₁ = -4
a₂ = -8
Now, for the given sequence to be an A.P,
Common difference (d) = a₁ - a = a₂ - a₁
Here
a₁ - a = -4 - 0
= -4
Also,
a₂ - a₁ = -8 - (-4)
= -4
Since a₁ - a = a₂ - a₁
Hence, the given sequence is an A.P and its common difference is d =-4
(iii) 1/2,1/4,1/6,1/8, ...
Here,
First term (a) = 1/2
a₁ = 1/4
a₂ = 1/6
Now, for the given to sequence to be an A.P,
Common difference (d) = a₁ - a = a₂ - a₁
Here,
a₁ - a = (1/4)-(1/2)
= (1 - 2)/4
= (-1)/4
Also,
a₁ - a = (1/6)-(1/4)
= (2 - 3)/12
= (-1)/12
Since  = a₁ - a ≠ a₂ - a₁
Hence, the given sequence is not an A.P
(iv) 12, 2, −8, −18, ...
Here,
First term (a) = 12
a₁ = 2
a₂ = -8
Now, for the given to sequence to be an A.P,
Common difference (d) = a₁ - a = a₂ - a₁
Here,
a₁ - a = 2 - 12
= -10
Also,
a₂ - a₁ = -8 - 2
= -10
Since a₁ - a = a₂ - a₁
Hence, the given sequence is an A.P with the common difference d = -10
(v) 3, 3, 3, 3, ...
Here,
First term (a) = 3
a₁ = 3
a₂ = 3
Now, for the given to sequence to be an A.P,
Common difference (d) = a₁ - a = a₂ - a₁
Here,
= a1 - a = 3 - 3
= 0
Also,
a₂ - a₁ = 3 - 3 = 0
Since
= a₁ - a = a₂ - a₁
Hence, the given sequence is an A.P and its common difference is d = 0
(vi) p, p + 90, p + 180 p + 270, ... where p = (999)⁹⁹⁹
Here,
First term (a) = p
a₁ = p + 90
a₂ = p + 180
Now, for the given to sequence to be an A.P,
Common difference (d) = a₁ - a = a₂ - a₁
Here,
a₁ - a = p + 90 - p
= 90
Also,
a₂ - a₁ = p + 180 - p - 90
= 90
Since a₁ - a = a₂ - a₁
Hence, the given sequence is an A.P and its common difference is d = 90
(vii) 1.0, 1.7, 2.4, 3.1, ...
Here,
First term (a) = 1.0
a₁ = 1.7
a₂ = 2.4
Now, for the given to sequence to be an A.P,
Common difference (d) = a₁ - a = a₂ - a₁
Here,
a₁ - a = 1.7 - 1.0
= 0.7
Also,
a₂ - a₁ = 2.4 - 1.7
= 0.7
Since a₁ - a = a₂ - a₁
Hence, the given sequence is an A.P and its common difference is d = 0.7
(viii) −225, −425, −625, −825, ...
Here,
First term (a) = −225
a₁ = -425
a₂ = -625
Now, for the given to sequence to be an A.P,
Common difference (d) = a₁ - a = a₂ - a₁
Here,
a₁ - a = -425 - (-225)
= -200
Also,
a₂ - a₁ = -625 - (-425)
= -200
Since a₁ - a = a₂ - a₁
Hence, the given sequence is an A.P and its common difference is d = -200
(ix) 10, 10 + 2⁵, 10 + 2⁶, 10 + 2⁷,...
Here,
First term (a) = 10
a₁ = 10 + 2⁵
a₂ = 10 + 2⁶
a₃ = 10 + 2⁷
Now, for the given to sequence to be an A.P,
Common difference (d) = a₁ − a = a₂ − a₁ 
Here,
a₂ - a₁ = 10 + 2⁶ - 10 - 2⁵
= 64 - 32
= 32
Also,
a₃ - a₂ = 10 + 2⁷ - 10 - 2⁶
= 128 - 64
= 64
Since a₁ - a ≠ a₂ - a₁
Hence, the given sequence is not an A.P.
(x) a + b, (a + 1) + b, (a + 1) + (b + 1), (a + 2) + (b + 1), (a + 2) + (b + 2), ...
Here,
First term (a) = a + b
a₁ = (a + 1) + b
a₂ = (a + 1)+(b + 1)
Now, for the given to sequence to be an A.P,
Common difference (d) = a₁ − a = a₂ − a₁ 
Here,
a₁ − a = a + 1 + b - a - b
= 1
Also,
a₂ - a₁ = a + 1 + b + 1 - a - 1 - b
= 1
Since a₁ − a = a₂ − a₁ 
Hence, the given sequence is an A.P and its common difference is d = 1
(xi) 1², 3², 5², 7², ...
Here,
First term (a) = 1²
a₁ = 3²
a₂ = 5²
Now, for the given to sequence to be an A.P,
Common difference (d) = a₁ − a = a₂ − a₁ 
Here,
a₁ - a = 3² - 1²
= 9 - 1
= 8
Also,
a₂ - a₁ = 5² - 3²
= 25 - 9
= 16
Since a₁ − a ≠ a₂ − a₁ 
Hence, the given sequence is not an A.P
(xii) 1², 5², 7², 73, ...
Here,
First term (a) = 1²
a₁ = 5²
a₂ = 7²
Now, for the given to sequence to be an A.P,
Common difference (d) = a₁ - a = a₂ - a₁
Here,
a₂ - a₁ = 5² - 1²
= 25 - 1
= 24
Also,
a₃ − a₂ = 7² − 5² = 49 − 25 = 24
Since a₁ - a = a₂ - a₁
Hence, the given sequence is an A.P with the common difference d = 24.