Chapter 1 - Real Numbers, RD Sharma Solutions - (Part - 8) | RD Sharma Solutions for Class 10 Mathematics PDF Download

Page No 1.49

Q.13. Prove that 2 + 5√3 is an irrational number, given that √3 is an irrational number.
Ans. Let us assume that 2 + 5√3 is a rational number.
Thus, 2 + 5√3 can be represented in the form of p/q, where p and q both are integers, q ≠ 0, p and q are co-prime numbers.
2 + 5√3 = p / q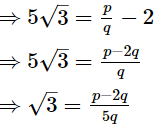

since, (hp - 2q/5q is rational ⇒ √3 is rational. 
But, it is given that √3 is an irrational number.
Therefore, our assumption is wrong.
Hence, 2 + 5√3 is an irrational number.

Q.14. Prove that for any prime positive integer p, √p is an irrational number.
Ans. Let us assume that √p is rational .Then, there exist positive co primes a and b such that
√p = a/b
p = (a/b)²
⇒ p = a^2/b²
⇒ pb² = a²
⇒ pb² = a²
⇒ p/a²
⇒ p/a
⇒ a = pc for some positive integer c
⇒ b²p = a²
⇒ b²p = p²c² (∵ a = pc)
⇒ p/b² (since p/c² p)
⇒ p/b
⇒ p/a and p/b
This contradicts the fact that a and b are co primes
Hence √p is irrational

Page No 1.50

Q.15. If p, q are prime positive integers, prove that √p + √q is an irrational number.
Ans. Let us assume that √p + √q is rational. Then, there exist positive co primes a and b such that
√p + √q = a / b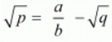 





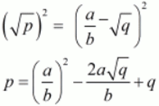
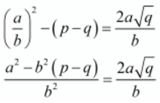
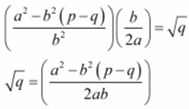
Here we see that √q is a rational number which is a contradiction as we know that √q is an irrational number
Hence √p + √q is irrational.

Page No 1.56

Q.1. Without actually performing the long division, state whether state whether the following rational numbers will have a terminating decimal expansion or a non-terminating repeating decimal expansion. 
(i) 23/8
Ans. The given number is 23/8
Here, 8 = 2³ and 2 is not a factor of 23. 
So, the given number is in its simplest form. 
Now, 8 = 2³ is of the form 2^m × 5ⁿ, where m = 3 and n = 0. 
So, the given number has a terminating decimal expansion.

(ii) 125/441
Ans. The given number is 125 / 441
Here, 441 = 3² × 7² and none of 3 and 7 is a factor of 125.
So, the given number is in its simplest form.
Now, 441 = 3² × 7² is not of the form 2^m × 5ⁿ.
So, the given number has a non-terminating repeating decimal expansion.

(iii) 35/50 [NCERT]
Ans. The given number is 35 / 50 and HCF(35, 50) = 5. 
∴ 35 / 50 = 35 ÷ 5 / 50 ÷ 5 = 7 / 10
Here, 7 / 10 is in its simplest form. 
Now, 10 = 2 × 5 is of the form 2^m × 5ⁿ, where m = 1 and n = 1.
So, the given number has a terminating decimal expansion.

(iv) 77/210 [NCERT]
Ans. The given number is 77 / 210 and HCF(77, 210) = 7. 
∴ 77 / 210 = 77 ÷ 7 / 210 ÷ 7 = 11 / 30
Here, 11 / 30 is in its simplest form.
Now, 30 = 2 × 3 × 5 is not of the form 2^m × 5ⁿ. So, the given number has a non-terminating repeating decimal expansion.

(v) 129/2² x 5⁷ x 7¹⁷
Ans. Clearly, none of 2, 5 and 7 is a factor of 129.
So, the given number is in its simplest form.
Now, 2² × 5⁷ × 7¹⁷ is not of the form 2^m × 5ⁿ.
So, the given number has a non-terminating repeating decimal expansion.

(vi) 987/10500
Ans. The given number is 987 / 10500.
987 / 10500 = 987 ÷ 21 / 10500 ÷ 21 = 47 / 500
Now, 500 = 2² × 5³ 
The denominator can be written in the form of 2^m × 5ⁿ.
So, the given number has a terminating decimal expansion.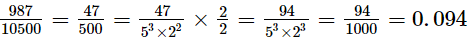


Q.2. Write down the decimal expansions of the following rational numbers by writing their denominators in the form 2^m × 5ⁿ, where, m, n are non-negative integers.

(i) 3/8
Ans. The given number is 3/8
Clearly, 8 = 2³ is of the form 2^m × 5ⁿ, where m = 3 and n = 0.
So, the given number has terminating decimal expansion.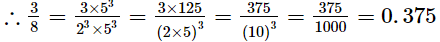 

(ii) 13/125
Ans. The given number is 13/125.
Clearly, 125 = 5³ is of the form 2^m × 5ⁿ, where m = 0 and n = 3.
So, the given number has terminating decimal expansion.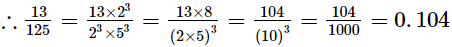 

(iii) 7/80
Ans. The given number is 7/80.
Clearly, 80 = 2⁴ × 5 is of the form 2^m × 5ⁿ, where m = 4 and n = 1.
So, the given number has terminating decimal expansion.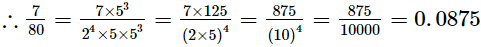

(iv) 14588/625
Ans. The given number is 14588/625.
Clearly, 625 = 5⁴ is of the form 2^m × 5ⁿ, where m = 0 and n = 4.
So, the given number has terminating decimal expansion.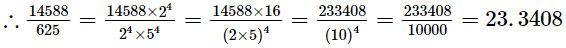

(v) 129/2² x 5⁷[NCERT]
Ans. The given number is 129/2² x 5⁷.
Clearly, 2² × 5⁷ is of the form 2^m × 5ⁿ, where m = 2 and n = 7.
So, the given number has terminating decimal expansion.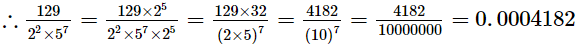 

Page No 1.57

Q.3. Write the denominator of the rational number 257/5000 in the form 2^m × 5ⁿ, where m,n are non-negative integers. Hence, write the decimal expansion, without actual division.
Ans. The given number is 257/5000.
Now, 5000 = 2³ × 5⁴
Clearly, 2 and 5 are factors of 5000.
The denominator can be written in the form of 2^m × 5ⁿ.
So, the given number has a terminating decimal expansion.


Q.4. What can you say about the prime factorisations of the denominators of the following rationals:

(i) 43.123456789 
Ans. Since 43.123456789 has terminating decimal expansion.
So, its denominator is of the form 2^m × 5ⁿ, where m, n are non-negative integers.

(ii)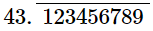
Ans. Since 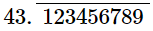has non-terminating decimal expansion.
So, its denominator has factors other than 2 or 5. 

(iii)
Ans. Since 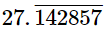has non-terminating decimal expansion.
So, its denominator has factors other than 2 or 5.  

(iv) 0.120120012000120000 ...
Ans. Since 0.120120012000120000 ... has non-terminating decimal expansion.
So, its denominator has factors other than 2 or 5.

Q.5. A rational number in its decimal expansion is 327.7081. What can you say about the prime factor of q , when this number is expressed in the form p / q? Give reasons.
Ans. Since 327.7081 is a terminating decimal number, therefore, it can be represented as a rational number. 
Also, its denominator must be in the form 2^m × 5ⁿ. 
Thus, 
327.7081=3277081 / 10000 = p / q
∴ q = 10000 = 2 × 2 × 2 × 2 × 5 × 5 × 5 × 5 = 2⁴ × 5⁴ 
Hence, the prime factorization of q contains only factors of 2 and 5.

Q.1. The exponent of 2 in the prime factorization of 144, is
(a) 4
(b) 5
(c) 6
(d) 3 
Ans. (a)
Solution. Using the factor tree for prime factorization, we have: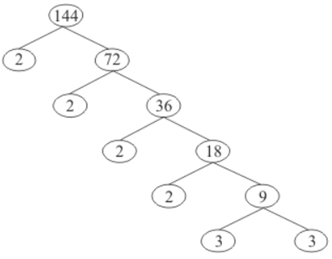 
Therefore,
144 = 2 x 2 x 2 x 2 x 3 x 3
144 = 2⁴ x 3²
Thus, the exponent of 2 in 144 is 4.

Q.2. The LCM of two numbers is 1200. Which of the following cannot be their HCF?
(a) 600
(b) 500
(c) 400
(d) 200
Ans. (b)
It is given that the LCM of two numbers is 1200.
We know that the HCF of two numbers is always the factor of LCM
Checking all the options:
(a) 600 is the factor of 1200.
So this can be the HCF.
(b) 500 is not the factor of 1200.
So this cannot be the HCF.
(c) 400 is the factor of 1200.
So this can be the HCF.
(d) 200 is the factor of 1200.
So this can be the HCF.

Q.3. If n = 2³ ✕ 3⁴ ✕ 5⁴ ✕ 7, then the number of consecutive zeros in n, where n is a natural number, is
(a) 2
(b) 3
(c) 4
(d) 7
Ans. (b)
Since, it is given that 
n = 2³ × 3⁴ × 5⁴ × 7 
= 2³ × 5⁴ × 3⁴ × 7
= 2³ × 5³ × 5 × 3⁴ × 7
= (2 × 5)³ × 5 × 3⁴ × 7
= 5 × 4 × 7 × (10)³ 
So, this means the given number n will end with 3 consecutive zeroes.

Q.4. The sum of the exponents of the prime factors in the prime factorization of 196, is
(a) 1
(b) 2
(c) 4
(d) 6
Ans. (c) 
Solution. Using the factor tree for prime factorization, we have: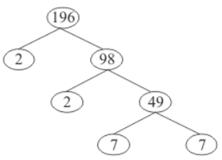
Therefore,
196 = 2 x 2 x 7 x 7
196 = 2² x 7²
The exponents of 2 and 7 are 2 and 2 respectively.
Thus the sum of the exponents is 4.

Page No 1.58

Q.5. The number of decimal place after which the decimal expansion of the rational number 23/(2² x 5) will terminate, is 
(a) 1
(b) 2
(c) 3
(d) 4
Ans. (b)
Solution. We have, 
23/(2² x 5)
Theorem states:  
Let x = p / q be a rational number, such that the prime factorization of q is of the form 2^m x 5ⁿ, where m and n are non-negative integers.
Then, x has a decimal expression which terminates after k places of decimals, where k is the larger of m and n.
This is given that the prime factorization of the denominator is of the form 2^m x 5ⁿ.
Hence, it has terminating decimal expansion which terminates after 2 places of decimal.

Q.6. If p₁ and p₂ are two odd prime numbers such that p₁ > p₂, then p²₁ − p²₂ is 
(a) an even number 
(b) an odd number 
(c) an odd prime number 
(d) a prime number 
Ans. (a)
Solution. Let the two odd prime numbers p₁ and p₂ be 5 and 3.
Then,
p²₁ = 5²
= 25
And
p²₂ = 3²
= 9
Thus,
p²₁ - p²₂ = 25 - 9
= 16
16 is even number.
Take another example, with p₁ and p₂ be 11 and 7.
Then,
 p²₁ = 11²
= 121
And
p²₂ = 7²
= 49
Thus,
p²₁ - p²₂ = 121 - 49
= 72
72 is even number.
Thus, we can say that p²₁ - p²₂ is even number
In general the square of odd prime number is odd. Hence the difference of square of two prime numbers is odd.

Q.7. If two positive ingeters a and b are expressible in the form a = pq² and b = p³q; p, q being prime number, then LCM (a, b) is
(a) pq
(b) p³q³ 
(c) p³q² 
(d) p²q²
Ans. (c)
Solution. Two positive integers are expressed as follows:
a = pq²
b = p³q
p and q are prime numbers.
Then, taking the highest powers of p and q in the values for a and b we get:
LCM (a, b) = p³q²

Q.8. In Q.No. 7, HCF (a, b) is
(a) pq
(b) p³q³ 
(c) p³q² 
(d) p²q²
Ans. (a)
Solution. Two positive integers are expressed as follows:
a = pq²
b = p³q
p and q are prime numbers.
Then, taking the smallest powers of p and q in the values for a and b we get
HCF (a, b) = pq

Q.9. If two positive integers m and n are expressible in the form m = pq³ and n = p³q², where p, q are prime numbers, then HCF (m, n) =
(a) pq
(b) pq² 
(c) p³q² 
(d) p²q²
Ans. (b)
Solution. Two positive integers are expressed as follows:
m = pq³
n = p³q²
p and q are prime numbers.
Then, taking the smallest powers of p and q in the values for m and n we get
HCF (m, n) = pq²

Q.10. If the LCM of a and 18 is 36 and the HCF of a and 18 is 2, then a =
(a) 2
(b) 3
(c) 4
(d) 1
Ans. (c)
Solution. LCM (a, 18) = 36
HCF (a, 18) = 2
We know that the product of numbers is equal to the product of their HCF and LCM.
Therefore,
18a = 2(36)
a = (2(36))/18
a = 4