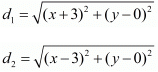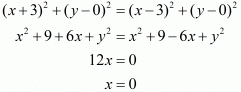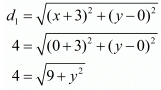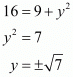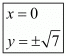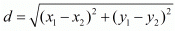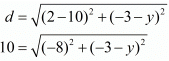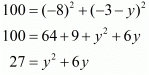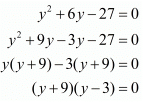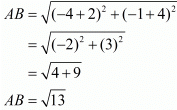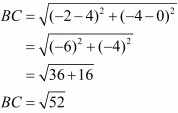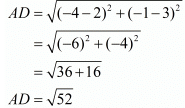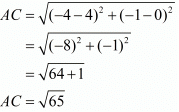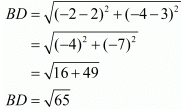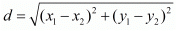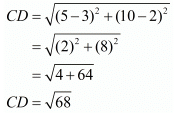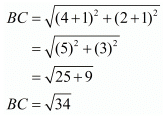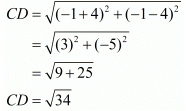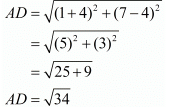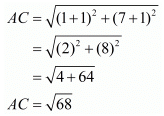Chapter 7 - Coordinate Geometry, RD Sharma Solutions - (Part-1) | RD Sharma Solutions for Class 10 Mathematics PDF Download
Page No 6.15
Ques.1. Find the distance between the following pair of points:
(i) (−6, 7) and (−1, −5)
(ii) (a+b, b+c) and (a−b, c−b)
(iii) (asinα, −bcosα) and (−acos α, bsin α)
(iv) (a, 0) and (0, b)
Ans. The distance d between two points (x1, x1) and (x2, x2) is given by the formula 
(i) The two given points are (−6, 7) and (−1, −5)
The distance between these two points is

Hence the distance is 13 units.
(ii) The two given points are (a+b,b+c) and (a-b,c-b)
The distance between these two points is

Hence the distance is 
(iii) The two given points are  and
and
The distance between these two points is

Hence the distance is
(iv) The two given points are (a, 0) and (0, b)
The distance between these two points is

Hence the distance is 
Page No 6.15
Ques.2. Find the value of a when the distance between the points (3, a) and (4, 1) is √10.
Ans. The distance d between two points and (x2,y2) is given by the formula  The distance between two points (3,a) and (4,1) is given as √10. Substituting these values in the formula for distance between two points we have,
The distance between two points (3,a) and (4,1) is given as √10. Substituting these values in the formula for distance between two points we have,

Now, squaring the above equation on both sides of the equals sign

Thus we arrive at a quadratic equation. Let us solve this now,

The roots of the above quadratic equation are thus 4 and −2.
Thus the value of ‘a’ could either be .
.
Page No 6.15
Ques.3. If the points (2, 1) and (1, −2) are equidistant from the point (x, y), show that x + 3y = 0.
Ans. The distance d between two points (x1,y1) and (x2,y2) is given by the formula 
Here it is said that the points (2, 1) and (1, −2) are equidistant from (x, y).
Let d1 be the distance between (2, 1) and (x, y).
Let d2 be the distance between (1, −2) and (x, y).
So, using the distance formula for both these pairs of points we have


Now since both these distances are given to be the same, let us equate both d1 and d2

Squaring on both sides we have,

Hence we have proved that when the points (2, 1) and (1,−2) are equidistant from (x, y) we have  .
.
Page No 6.15
Ques.4. Find the values of x, y if the distances of the point (x, y) from (−3, 0) as well as from (3, 0) are 4.
Ans. The distance d between two points (x1,y1) and (x2,y2) is given by the formula 
It is said that (x, y) is equidistant from both (−3,0) and (3,0).
Let be the distance between (x, y) and (−3,0).
Let be the distance between (x, y) and (3,0).
So, using the distance formula for both these pairs of points we have

Now since both these distances are given to be the same, let us equate both d1 and d2.

Squaring on both sides we have,

It is also said that the value of both and is 4 units.
Substituting the value of ‘x’ in the equation for either or we can get the value of ‘y’.

Squaring on both sides of the equation we have,

Hence the values of ‘x’ and ‘y’ are 
Page No 6.15
Ques.5. The length of a line segment is of 10 units and the coordinates of one end-point are (2, −3). If the abscissa of the other end is 10, find the ordinate of the other end.
Ans. The distance d between two points (x1,y1) and (x2,y2) is given by the formula 
Here it is given that one end of a line segment has co−ordinates (2,−3). The abscissa of the other end of the line segment is given to be 10. Let the ordinate of this point be ‘y’.
So, the co−ordinates of the other end of the line segment is (10, y).
The distance between these two points is given to be 10 units.
Substituting these values in the formula for distance between two points we have,

Squaring on both sides of the equation we have,

We have a quadratic equation for ‘y’. Solving for the roots of this equation we have,

The roots of the above equation are ‘−9’ and ‘3’.
Thus the ordinates of the other end of the line segment could be -9 or 3.
Page No 6.15
Ques.6. Show that the points (−4, −1), (−2, −4) (4, 0) and (2, 3) are the vertices points of a rectangle.
Ans. The distance d between two points (x1,y1) and (x2,y2) is given by the formula

In a rectangle, the opposite sides are equal in length. The diagonals of a rectangle are also equal in length.
Here the four points are A(−4,−1), B(−2,−4), C(4,0) and D(2,3).
First let us check the length of the opposite sides of the quadrilateral that is formed by these points.


We have one pair of opposite sides equal.
Now, let us check the other pair of opposite sides.


The other pair of opposite sides are also equal. So, the quadrilateral formed by these four points is definitely a parallelogram.
For a parallelogram to be a rectangle we need to check if the diagonals are also equal in length.


Now since the diagonals are also equal we can say that the parallelogram is definitely a rectangle.
Hence we have proved that the quadrilateral formed by the four given points is a rectangle.
Page No 6.15
Ques.7. Show that the points A (1, −2), B (3, 6), C (5, 10) and D (3, 2) are the vertices of a parallelogram.
Ans. The distance d between two points (x1, y1) and (x2, y2) is given by the formula 
In a parallelogram the opposite sides are equal in length.
Here the four points are A(1, −2), B(3, 6), C(5, 10) and D(3, 2).
Let us check the length of the opposite sides of the quadrilateral that is formed by these points.


We have one pair of opposite sides equal.
Now, let us check the other pair of opposite sides.


The other pair of opposite sides is also equal. So, the quadrilateral formed by these four points is definitely a parallelogram.
Hence we have proved that the quadrilateral formed by the given four points is a parallelogram.
Page No 6.15
Ques.8. Prove that the points A(1, 7), B (4, 2), C(−1, −1) D (−4, 4) are the vertices of a square.
Ans. The distance d between two points (x1,y1) and (x2,y2) is given by the formula
In a square all the sides are equal in length. Also, the diagonals are equal in length in a square.
Here the four points are A(1, 7), B(4, 2), C(−1, −1) and D(−4, 4).
First let us check if all the four sides are equal.




Since all the sides of the quadrilateral are the same it is a rhombus.
For the rhombus to be a square the diagonals also have to be equal to each other.


Since the diagonals of the rhombus are also equal to each other the rhombus is a square.
Hence the quadrilateral formed by the given points is a square.
Page No 6.15
Ques.9. Prove that the points (3, 0), (6, 4) and (−1, 3) are vertices of a right-angled isosceles triangle.
Ans. The distance d between two points (x1,y1) and (x2,y2) is given by the formula
In an isosceles triangle there are two sides which are equal in length. Here the three points are A(3, 0), B(6, 4) and C(−1, 3).
Let us check the length of the three sides of the triangle.
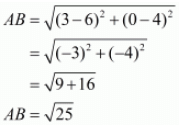
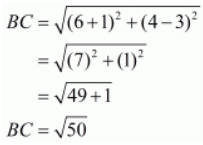
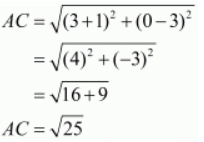
Here, we see that two sides of the triangle are equal. So the triangle formed should be an isosceles triangle.
We can also observe that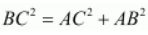
Hence proved that the triangle formed by the three given points is an
Page No 6.15
Ques.10. Prove that (2, −2) (−2, 1) and (5, 2) are the vertices of a right angled triangle. Find the area of the triangle and the length of the hypotenuse.
Ans. The distance d between two points (x1,y1) and is given by the formula
In a right-angled triangle, by Pythagoras theorem, the square of the longest side is equal to the sum of squares of the other two sides in the triangle. Here the three points are A(2,−2), B(−2,1) and C(5,2).
Let us find out the lengths of all the sides of the triangle.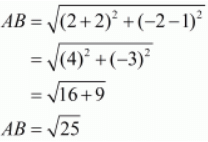
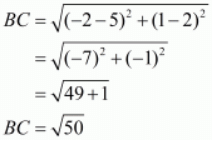

Here we have,
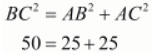
Since the square of the longest side is equal to the sum of squares of the other two sides the given triangle is a right-angled triangle
In a right angled triangle the area of the triangle ‘A’ is given by,
A=1/2(Product of both the sides containing the right angle).
In a right angled triangle the sides containing the right angle will not be the longest side.
Hence the area of the given right angled triangle is,
Hence the area of the given right-angled triangle is 12.5 square units.
In a right-angled triangle the hypotenuse will be the longest side. Here the longest side is ‘BC’.
Hence the hypotenuse of the given right-angled triangle is 5√2 units.
Page No 6.15
Ques.11. Prove that the points (2a, 4a), (2a, 6a) and (2a+3–√a3a, 5a) are the vertices of an equilateral triangle.
Ans. The distance d between two points (x1, x2) and is given by the formula
In an equilateral triangle all the sides have equal length.
Here the three points are A( 2a, 4a ), B( 2a, 6a ) and C( 2a+a√3, 5a).
Let us now find out the lengths of all the three sides of the given triangle.
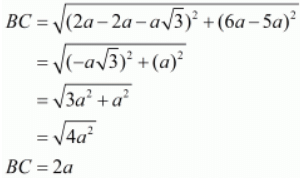
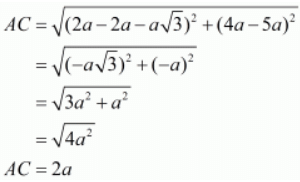
Since all the three sides have equal lengths the triangle has to be an equilateral triangle.
Page No 6.15
Ques.12. Prove that the points (2,3), (−4, −6) and (1, 3/2) do not form a triangle.
Ans. The distance d between two points (x1,y1) and (x2,y2) is given by the formula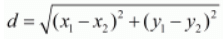
In any triangle the sum of lengths of any two sides need to be greater than the third side.
Here the three points are,A(2,3), B(-4,-6) and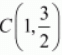
Let us now find out the lengths of all the three sides of the given triangle.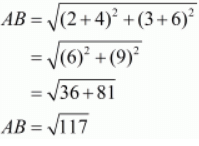
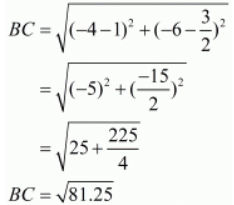
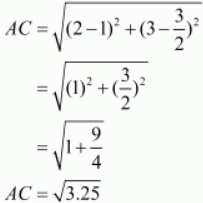
Here we see that, BC + AC AB
AB
This is in violation of the basic property of any triangle to exist. Therefore these points cannot give rise to a triangle.
Hence we have proved that the given three points do not form a triangle.
Page No 6.15
Ques.13. The points A(2, 9), B(a, 5) and C(5, 5) are the vertices of a triangle ABC right angled at B. Find the values of a and hence the area of ΔABC.
Ans.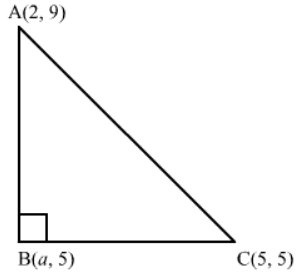
Consider the figure.
Using distance formula,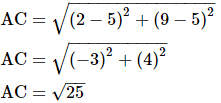
AC2 = 25 units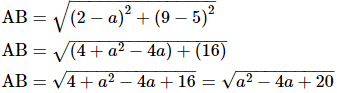
AB2 = (a2 - 4a + 20) units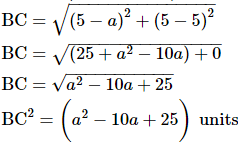
We are given that ABC is a right triangle right angled at B.
By Pythagoras theorem, we have
AC2 = AB2 + BC2
⇒25 = (a2− 4a + 20) + (a2−10a + 25)
⇒25 = 2a2−14a + 45
⇒2a 2−14a + 20 =0
⇒a2−7a + 10 =0
⇒a2 − 5a − 2a + 10 =0
⇒a(a−5)−2(a−5) =0
⇒(a−2)(a−5) =0
⇒a=2 or a =5
Page No 6.15
Ques.14. Show that the quadrilateral whose vertices are (2, −1), (3, 4) (−2, 3) and (−3,−2) is a rhombus.
Ans. The distance d between two points (x1,y1) and (x2,y2) is given by the formula
In a rhombus all the sides are equal in length.
Here the four points are A (2, −1), B (3, 4), C (−2, 3) and D (−3, −2).
First let us check if all the four sides are equal.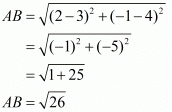
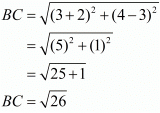
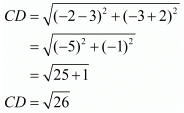
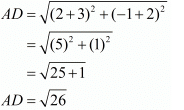
Here, we see that all the sides are equal, so it has to be a rhombus.
Page No 6.15
Ques.15. Two vertices of an isosceles triangle are (2, 0) and (2, 5). Find the third vertex if the length of the equal sides is 3.
Ans. The distance d between two points (x1,y1) and (x2,y2) is given by the formula
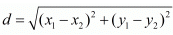
In an isosceles triangle two sides will be of equal length.
Here two vertices of the triangle is given as A (2, 0) and B (2, 5). Let the third side of the triangle be C(x, y)
It is given that the length of the equal sides is 3 units.
Let us now find the length of the side in which both the vertices are known.
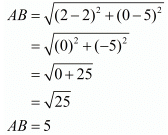
So, now we know that the side ‘AB’ is not one of the equal sides of the isosceles triangle.So, we have AC = BC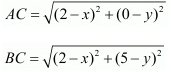
Equating these two equations we have,

Squaring on both sides of the equation we have,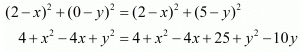
10y = 25
y = 5/2
y = 2.5
We know that the length of the equal sides is 3 units. So substituting the value of ‘y’ in equation for either ‘AC’ or ‘BC’ we can get the value of ‘x’.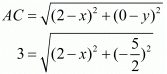
Squaring on both sides,
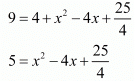
20 = 4x2 - 16x + 25
-5 = 4x2 - 16x
We have a quadratic equation for ‘x’. Solving for roots of the above equation we have,
4x2 - 16x + 5 = 0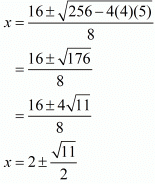
Hence the possible co−ordinates of the third vertex of the isosceles triangle are 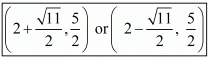 .
.
Page No 6.16
Ques.16. Which point on x-axis is equidistant from (5, 9) and (−4, 6)?
Ans. The distance d between two points (x1,y1) and (x2,y2) is given by the formula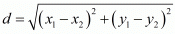
Here we are to find out a point on the x−axis which is equidistant from both the points A (5, 9) and B (−4, 6)
Let this point be denoted as C(x, y)
Since the point lies on the x-axis the value of its ordinate will be 0. Or in other words we have y = 0.
Now let us find out the distances from ‘A’ and ‘B’ to ‘C’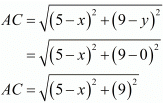
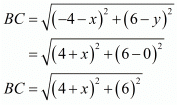
We know that both these distances are the same. So equating both these we get,
AC = BC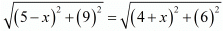
Squaring on both sides we have,
(5-x)2 + (9)2 = (4+x)2 + (6)2
25 + x2 - 10x + 81 = 16 + x2 + 8x + 36
18x = 54
x = 3
Hence the point on the x-axis which lies at equal distances from the mentioned points is (3,0).

|
Explore Courses for Class 10 exam
|

|
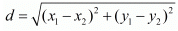
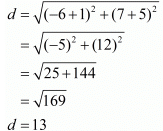
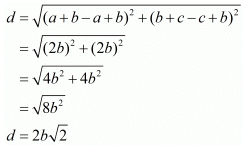
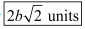
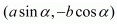 and
and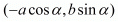
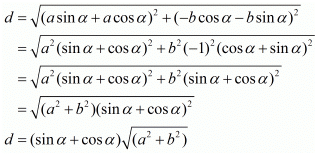

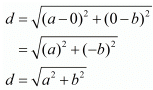
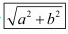
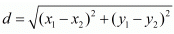 The distance between two points (3,a) and (4,1) is given as √10. Substituting these values in the formula for distance between two points we have,
The distance between two points (3,a) and (4,1) is given as √10. Substituting these values in the formula for distance between two points we have,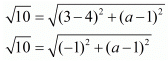
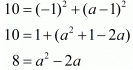
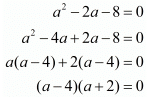
 .
.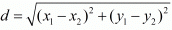


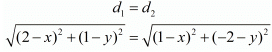
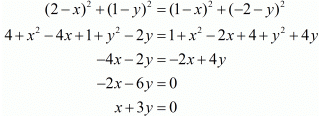
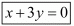 .
.