Chapter 3 - Pair Of Linear Equations In Two Variables, RD Sharma Solutions - (Part-7) | RD Sharma Solutions for Class 10 Mathematics PDF Download

Page No 3.12

Q.4. Gloria is walking along the path joining (−2, 3) and (2, −2), while Suresh is walking along the path joining (0, 5) and (4, 0). Represent this situation graphically.
Ans. Gloria is walking the path joining (−2, 3) and (−2, 2)
Suresh is walking the path joining (0, 5) and (4, 0)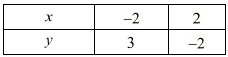


The graphical representations are


Q.5. On comparing the ratios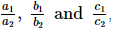and without drawing them, find out whether the lines representing the following pairs of linear equations intersect at a point, are parallel or coincide :
(i) 5x − 4y + 8 = 0
7x + 6y − 9 = 0
(ii) 9x + 3y + 12 = 0
18x + 6y + 24 = 0
(iii) 6x − 3y + 10 = 0
2x − y + 9 = 0
Ans. (i) Given equation are: 5x + 4y + 8 = 0
7x + 6y − 9 = 0
Where, a₁ = 5, b₁ = -4, c₁ = 8
a₂ = 7, b₂ = 6, c₃ = - 9
We have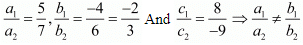
Thus the pair of linear equation is intersecting.
(ii) Given equation are: 9x + 3y + 12 = 0
18x + 6y + 24 = 0
Where, a₁ = 9, b₁ = 3, c₁ = 12
a₂ = 18, b₂ = 6, c₂ = 24
We have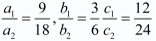

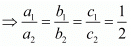
Thus the pair of linear is coincident lines.
(iii) Given equation are: 6x -3y + 10 = 0
2x - y + 9 = 0
Where, a₁ = 6, b₁ = -3, c₁ = 10
a₂ = 2, b₂ = - 1, c₂ = 9
We have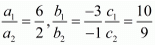

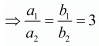
Thus the pair of line is parallel lines.

Q.6. Given the linear equation 2x + 3y − 8 = 0, write another linear equation in two variables such that the geometrical representation of the pair so formed is:
(i) intersecting lines
(ii) parallel lines
(iii) coincident lines
Ans. (i) Given the linear equation are:2x + 3y - 8 = 0
We know that intersecting condition: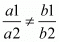

Where a₁ = 2, b₁ = 3, c₁ = - 8
Hence the equation of other line is x + 2y - 4 = 0
(i) We know that parallel line condition is:
Where a₁ = 2, b₁ = 3, c₁ = - 8
Hence the equation of other line is x + 2y - 4 = 0
(ii) We know that parallel line condition is: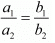
Where a₁ = 2, b₁ = 3, c₁ = -8
Hence the equation is 2x + 6y - 12 = 0
(iii) We know that coincident line condition is: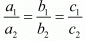
Where a₁ = 2, b₁ = 3, c₁ = -8
Hence the equation is 4x + 6y - 16 = 0

Q.7. The cost of 2kg of apples and 1 kg of grapes on a day was found to be Rs 160. After a month, the cost of 4 kg of apples and 2kg of grapes is Rs. 300 Represent th situation algebraically and geometrically.
Ans. Let the cost of 1 kg of apples be Rs x.
And, cost of 1 kg of grapes = Rs y
According to the question, the algebraic representation is
2x + y = 160
4x + 2y = 300
For 2x + y = 160,
y = 160 - 2x
The solution table is

For 4x + 2y = 300,
y =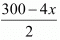
The solution table is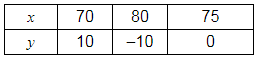

The graphical representation is as follows.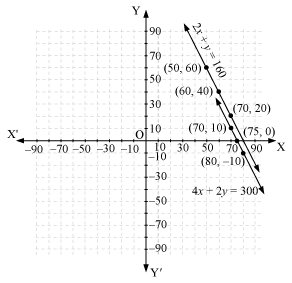

Page No 3.29

Q.1. Solve the following systems of equations graphically:
x + y = 3
2x + 5y = 12
Ans. The given equations are:
x + y = 3 ....(i)
2x + 5y = 12 ....(ii)
Putting x = 0 in equation (i) we get:
⇒ 0 + y = 3
⇒ y = 3
x = 3, y = 0
Putting y = 0 in equation (ii) we get:
⇒ x + 0 = 3
⇒ x = 3
x = 3, y = 0
Use the following table to draw the graph.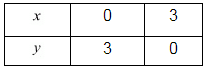

Draw the graph by plotting the two points A(0,3) and B(3,0) from table.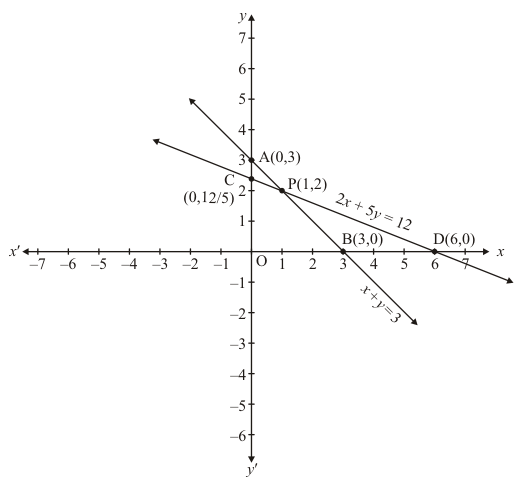

Graph of the equation (ii):
⇒ 2x + 5y = 12 ....(ii)
Putting x = 0 in equation (ii), we get:
⇒ 2 x o + 5y = 12
⇒ 5y = 12
⇒ y = 12/5
x = 0, y = 12/5
Putting y = 0 in equation (ii), we get:
⇒ 2x + 5 x 0 = 12
⇒ 2x = 12
⇒ x = 6
x = 6, y = 0
Use the following table to draw the graph.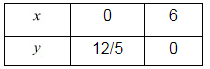

Draw the graph by plotting the two points C(0,12/5),D(0,6/0) from the table.
The two lines intersect at point P(1,2)
Hence, x = 1 and y = 2 is the solution.

Q.2. Solve the following systems of equations graphically:
x − 2y = 5
2x + 3y = 10
Ans. The given equations are
x − 2y = 5     ....(i)
2x + 3y = 10     ....(ii)
Putting x = 0 in equation (i), we get:
⇒ 0 - 2y = 5
⇒ y = - 5 /2
x = 0, y = -5/2
Putting y = 0 in equation (i), we get:
⇒ x + 2 x 0 = 5
⇒ x = 5
x = 5, y = 0
Use the following table to draw the graph.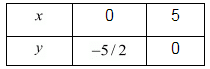

Draw the graph by plotting the two points A(0, - 5/2)and B (5,0) from table.

Graph the equation (ii):
⇒ 2x + 3y = 10......(ii)
Putting x = 0 in equation (ii), we get:
⇒ 2 x 0 + 3y = 10
⇒ y = 10/3
x = 0, y = 10/3
Putting y = 0 in equation (ii), we get:
⇒ 2x + 3 x 0 = 10
⇒ x = 5
x = 5, y = 0
Use the following table to draw the graph.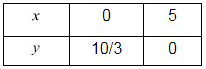

Draw the graph by plotting the two points C(0,10/3) and B (5,0) from table.
The two lines intersects at point B(5,0).
Hence x = 5, y = 0 is the solution.

Page No 3.29

Q.3. Solve the following systems of equations graphically:
3x + y + 1 = 0
2x − 3y + 8 = 0
Ans. The given equations are
3x + y + 1 = 0  ...(i)
2x − 3y + 8 = 0  ...(ii)
Putting x = 0 in equation (i), we get:
⇒ 3 x 0 + y = - 1
⇒ y = - 1
x = 0, y = - 1
Putting y = 0 in equation (i), we get:
⇒ 3x + 0 = - 1
⇒ x = - 1/3
x = -1/3,  y = 0
Use the following table to draw the graph.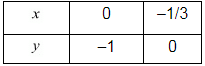

Draw the graph by plotting the two points A(0, - 1) and B(-1/3,0) from table.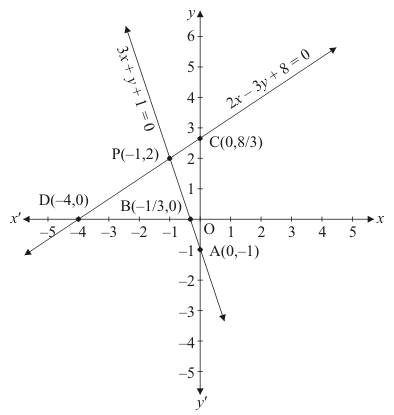

Graph of the equation ...(ii)
2x - 3y = - 8 ...(ii)
Putting x = 0 in equation (ii) we get
⇒ 2 x 0 - 3y = - 8
⇒ y = 8/3
x = 0, y = 8/3
Putting y = 0 in equation (ii), we get
⇒ 2x - 3 x 0 = -8
⇒ x = -4
x = -4, y = 0
Use the following table to draw the graph.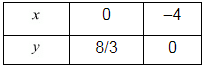

Draw the graph by plotting the two points C(0,8/3) and D(-4, 0)  from table.
The two lines intersect at points P(-1,2).
Hence x = - 1, y = 2  is the solution.

Q.4. Solve the following systems of equations graphically:
2x + y − 3 = 0
2x − 3y − 7 = 0
Ans. The given equations are
⇒ 2x + y − 3 = 0  ...(i)
⇒ 2x − 3y − 7 = 0  ...(ii)
Putting x = 0 in equation (i), we get:
⇒ 2 x 0 + y = 3
⇒ y = 3
x = 0, y = 3
Putting y = 0 in equation (i), we get:
⇒ 2x + 0 = 3
⇒ x = 3/2
x = 3/2,  y = 0
Use the following table to draw the graph.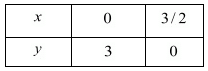

Draw the graph by plotting the two points A (0,3) and B (3/2,0) from table.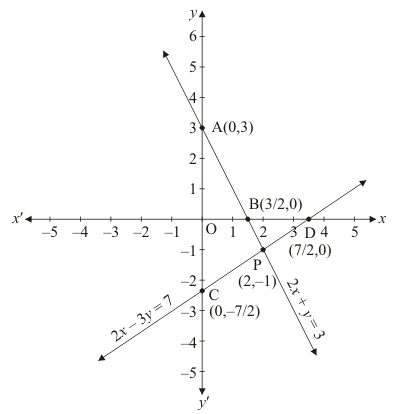

Graph of the equation….(ii):
2x - 3y = 7
Putting x = 0  in equation (ii) we get:
⇒ 2 x 0 - 3y = 7
⇒ y = -7/3
x = 0, y = -7/3
Putting y = 0 in equation (ii), we get
⇒ 2x - 3 x 0 = 7
⇒ x = 7/2
x = 7/2, y = 0
Use the following table to draw the graph.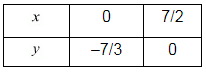

Draw the graph by plotting the two points C(0,-7/2) and D(7/2,0) from table.
The two lines intersect at points P (2,-1).
Hence x = 2, y = -1 is the solution.

Q.5. Solve the following systems of equations graphically:
x – y + 1 = 0
3x + 2y – 12 = 0
Ans. The given equations are:
x – y + 1 = 0    ...(i)
3x + 2y – 12 = 0     ...(ii)
Solving equation (i), we get
x − y + 1 = 0
⇒ y = x + 1
When x = 0, y = 1
When x = 1, y = 2

Solving equation (ii), we get
3x + 2y − 12 = 0
⇒2y = 12 − 3x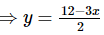

When x = 0, y = 6
When x = 4, y = 0

On plotting these points on a graph, we get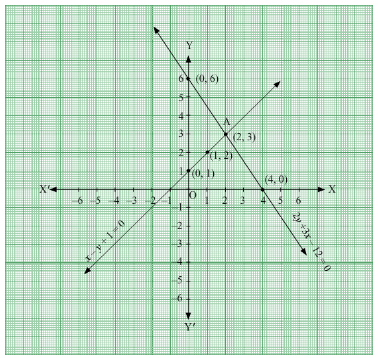

Hence, point A(2, 3) is the point of intersection.

Q.6. Solve the following systems of equations graphically:
x − 2y = 6
3x − 6y = 0
Ans. The given equations are:
x − 2y = 6   .....(i)
3x − 6y = 0   .....(ii)
Putting x = 0 in equation (i) we get:
⇒ 0 - 2y = 6
⇒ y = - 3
x = 0, y = -3
Putting y = 0 in equation (i) we get:
⇒ x - 2 x 0 = 6
⇒ y = 6
x = 6, y = 0
Use the following table to draw the graph.

Plotting the two points A(0,3) and B (6,0) equation (i) can be drawn.
Graph of the equation ….(ii):
3x - 6y = 0  ….(ii)
Putting x = 0 in equation (ii), we get:
⇒ 3 x 0 - 6y = 0
⇒ y = 0
x = 0, y = 0
Putting x = 2 in equation (ii), we get:
⇒ 3 x 2 - 6y = 0
⇒ y = 1
x = 2, y = 1
Use the following table to draw the graph.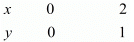

Draw the graph by plotting the two points  O(0,0) and D(2,1) from table.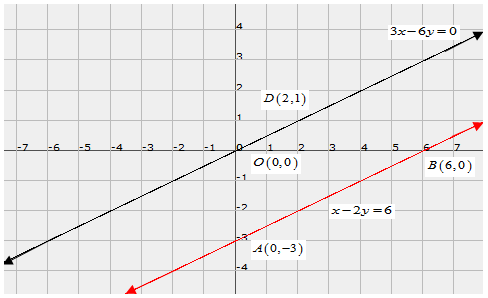

We see that the two lines are parallel, so they won’t intersect
Hence there is no solution

Q.7. Solve the following systems of equations graphically:
x + y = 4
2x − 3y = 3
Ans. The given equations are
x + y = 4  ...(i)
2x - 3y = 3  ...(ii)
Putting x = 0 in equation (i), we get:
⇒ 0 + y = 4
⇒ y = 4
∴ x = 0, y = 4
Putting y = 0 in equation (i), we get
⇒ x + 0 = 4
⇒ x = 4
∴ x = 4, y = 0
Use the following table to draw the graph.

Draw the graph by plotting the two points A(4,0) and B(4,0) from table.
Graph of the equation….(ii):
2x - 3y = 3 ….(ii)
Putting x = 0 in equation (ii) we get
⇒ 0 - 3y = 3
⇒ y = - 1
∴ x = 0, y = - 1
Putting y = 0 in equation (ii), we get:
⇒ 2x - 0 = 3
⇒ x = 3/2
∴ x = 3/2, y = 0
Use the following table to draw the graph.

Draw the graph by plotting the two points C(0,-1) and D (3/2,0) from table.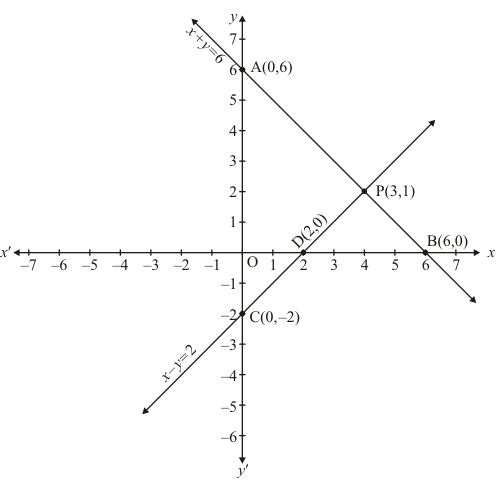

The two lines intersect at points P(3,1).
Hence x = 3, y = 1 is the solution.

Q.8. Solve the following systems of equations graphically:
2x + 3y = 4
x − y + 3 = 0
Ans. The given equations are:
2x + 3y = 4   ...(i)
x − y + 3 = 0   ...(ii)
Putting x = 0 in equation (i), we get:
⇒ 2 x 0 + 3y = 4
⇒ y = 4/3
x = 0, y = 4/3
Putting y = 0  in equation (i), we get:
⇒ 2x + 3 x 0 = 4
⇒ x = 2
x = 2, y = 0
Use the following table to draw the graph.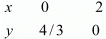

Draw the graph by plotting the two points A(0,4/3) and B(2,0) from table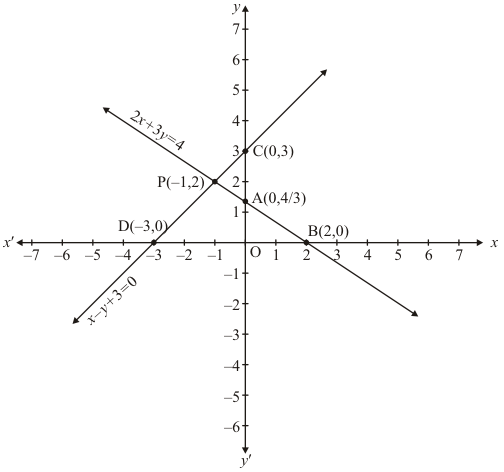

Graph of the equation….(ii):
x - y = -3   ….(ii)
Putting x = 0  in equation (ii) we get:
⇒ 0 - y = -3
⇒ y = 3
x = 0, y = 3
Putting y = 0 in equation (ii), we get:
⇒ 0 - y = - 3
⇒ y = 3
x = 0, y = 3
Use the following table to draw the graph.

Draw the graph by plotting the two points C(0,3) and D(-3,0) from table
The two lines intersect at points P(-1,2)
Hence, x = - 1 and y = 2 is the solution.

Q.9. Solve the following systems of equations graphically:
2x − 3y + 13 = 0
3x − 2y + 12 = 0
Ans. The given equations are:
2x − 3y + 13 = 0   ...(i)
3x − 2y + 12 = 0   ...(ii)
Putting x = 0 in equation (i), we get
⇒ 2 x 0 - 3y = - 13
⇒ y = 13/3
x = 0, y = 13/3
Putting y = 0 in equation (ii) we get
⇒ 2x - 3 x 0 = - 13
⇒ x = - 13/2
x = - 13/2, y = 0
Use the following table to draw the graph.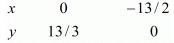

Draw the graph by plotting the two points A(0,13/2) and B(-13/2,0) from table.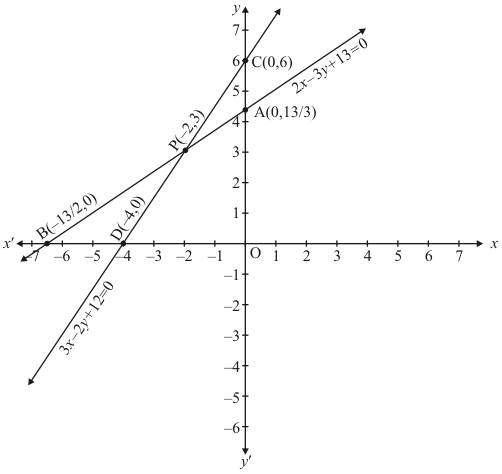

Graph of the equation….(ii):
3x - 2y = -12   ….(ii)
Putting x = 0 in equation (ii) we get:
⇒ 3x 0 - 2y = - 12
⇒ y = 6
x = 0, y = 6
Putting y = 0 in equation (ii), we get:
⇒ 3x - 2 x 0 = - 12
⇒ x = -4
x = -4, y = 0
Use the following table to draw the graph.

Draw the graph by plotting the two points C(0,6)and D(-4, 0) from table.
The two lines intersect at points P(-2, 3)
Hence, x = - 2 and y = 3 is the solution.