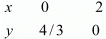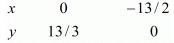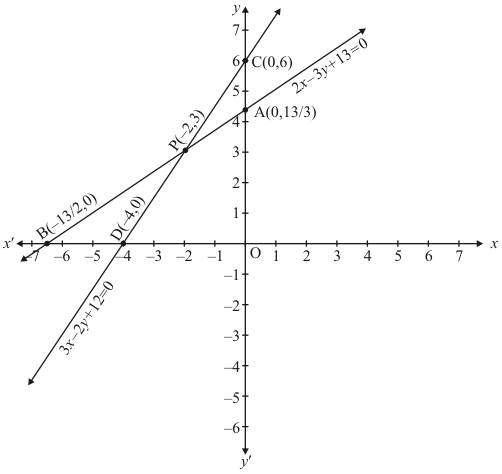Page No 3.29
Q.8. Solve the following systems of equations graphically:
2x + 3y = 4
x − y + 3 = 0
Ans. The given equations are:
2x + 3y = 4 ...(i)
x − y + 3 = 0 ...(ii)
Putting x = 0 in equation (i), we get:
⇒ 2 x 0 + 3y = 4
⇒ y = 4/3
x = 0, y = 4/3
Putting y = 0 in equation (i), we get:
⇒ 2x + 3 x 0 = 4
⇒ x = 2
x = 2, y = 0
Use the following table to draw the graph.

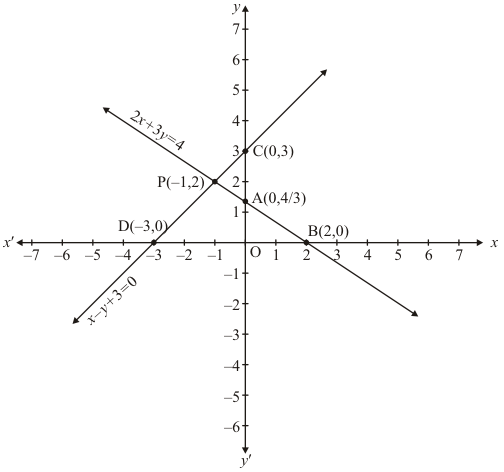
Draw the graph by plotting the two points A(0,4/3) and B(2,0) from table

Graph of the equation….(ii):
x - y = -3 ….(ii)
Putting x = 0 in equation (ii) we get:
⇒ 0 - y = -3
⇒ y = 3
x = 0, y = 3
Putting y = 0 in equation (ii), we get:
⇒ 0 - y = - 3
⇒ y = 3
x = 0, y = 3
Use the following table to draw the graph.

Draw the graph by plotting the two points C(0,3) and D(-3,0) from table
The two lines intersect at points P(-1,2)
Hence, x = - 1 and y = 2 is the solution.
Q.9. Solve the following systems of equations graphically:
2x − 3y + 13 = 0
3x − 2y + 12 = 0
Ans. The given equations are:
2x − 3y + 13 = 0 ...(i)
3x − 2y + 12 = 0 ...(ii)
Putting x = 0 in equation (i), we get
⇒ 2 x 0 - 3y = - 13
⇒ y = 13/3
x = 0, y = 13/3
Putting y = 0 in equation (ii) we get
⇒ 2x - 3 x 0 = - 13
⇒ x = - 13/2
x = - 13/2, y = 0
Use the following table to draw the graph.

Draw the graph by plotting the two points A(0,13/2) and B(-13/2,0) from table.

Graph of the equation….(ii):
3x - 2y = -12 ….(ii)
Putting x = 0 in equation (ii) we get:
⇒ 3x 0 - 2y = - 12
⇒ y = 6
x = 0, y = 6
Putting y = 0 in equation (ii), we get:
⇒ 3x - 2 x 0 = - 12
⇒ x = -4
x = -4, y = 0
Use the following table to draw the graph.

Draw the graph by plotting the two points C(0,6)and D(-4, 0) from table.
The two lines intersect at points P(-2, 3)
Hence, x = - 2 and y = 3 is the solution.
Q.10. Solve the following systems of equations graphically:
2x + 3y + 5 = 0
3x − 2y − 12 = 0
Ans. The given equations are
2x + 3y + 5 = 0….(i)
3x - 2y - 12 = 0….(ii)
Putting x = 0 in equation (i), we get:
⇒ 2 x 0 + 3y = -5
⇒ y = - 5/3
Putting y = 0 in equation (i), we get:
⇒ 2x + 3 x 0 = -5
⇒ x = -5/2
x = -5/2, y = 0
Use the following table to draw the graph.

Draw the graph by plotting the two points from table.

Graph of the equation ….(ii):
3x - 2y = 12 ….(ii)
Putting x = 0 in equation (ii) we get:
⇒ 3 x 0 - 2y = 12
⇒ y = -6
x = 0, y = - 6
Putting y = 0 in equation (ii), we get:
⇒ 3x - 2 x 0 = 12
⇒ x = 4
x = 4, y = 0
Use the following table to draw the graph.

Draw the graph by plotting the two points from table.
The two lines intersects at points P(2,-3)
Hence, x = 2 and y = -3 is the solution.
Q.11. Show graphically that each one of the following systems of equations has infinitely many solutions:
2x + 3y = 6
4x + 6y = 12
Ans. The given equations are
2x + 3y = 6 ….(i)
4x + 6y = 12 ...(ii)
Putting x = 0 in equation (i), we get:
⇒ 2 x 0 +3y = 6
⇒ y = 2
x = 0, y = 2
Putting y = 0 in equation (i), we get:
⇒ 2x + 3x = 6
⇒ x = 3
x = 3, y = 0
Use the following table to draw the graph.

Draw the graph by plotting the two points A(0,2) and B(3,0) from table.

Graph of the equation ….(ii):
4x + 6y = 12 ….(ii)
Putting x = 0 in equation (ii) we get:
⇒ 4x 0 + 6y = 12
⇒ y = 2
x = 0, y = 2
Putting y = 0 in equation (ii) we get:
⇒ 4x + 6 x 0 = 12
⇒ x = 3
x = 3, y = 0
Use the following table to draw the graph.

Draw the graph by plotting the two points C(0,2),D(3,0) from table.
Thus the graph of the two equations coincide
Consequently, every solution of one equation is a solution of the other.
Hence the equations have infinitely many solutions.
Q.12. Show graphically that each one of the following systems of equations has infinitely many solutions:
x − 2y = 5
3x − 6y = 15
Ans. The given equations are
x - 2y = 5 .....(i)
3x - 6y = 15 .....(ii)
Putting x = 0 in equation (i), we get:
⇒ 0 - 2y = 5
⇒ y = -5/2
x = 0, y = -5/2
Putting y = 0 in equations (i) we get:
⇒ x - 2 x 0 = 5
⇒ x = 5
x = 5, y = 0
Use the following table to draw the graph.

Draw the graph by plotting the two points A(0,-5/2) and B (5,0) from table

Graph of the equation ...(ii)
3x - 6y = 15 ...(ii)
Putting x = 0 in equations (ii), we get:
⇒ 3 x 0 - 6y = 15
⇒ y = -5/2
x = 0, y = -5/2
Putting y = 0 in equation (ii), we get:
⇒ 3x - 6 x 0 = 15
⇒ x = 5
x = 5, y = 0
Use the following table to draw the graph.

Draw the graph by plotting the two points C(0,-5/2) and D(5,0) from table.
Thus the graph of the two equations coincide
Consequently, every solution of one equation is a solution of the other.
Hence the equations have infinitely many solutions.
Q.13. Show graphically that each one of the following systems of equations has infinitely many solutions:
3x + y = 8
6x + 2y = 16
Ans. The given equations are
3x + y = 8 ...(i)
6x + 2y = 16 ...(ii)
Putting x = 0 in equation (i), we get:
⇒ 3x + 0 + y = 8
⇒ y = 8
x = 0, y = 8
Putting y = 0 in equation (i), we get:
⇒ 3x + 0 = 8
⇒ x = 8/3
x = 8/3, y = 0
Use the following table to draw the graph.

Draw the graph by plotting the two points A(0,8) and B(8/3,0) from table.

Graph of the equation….(ii):
6x + 2y = 16 ….(ii)
Putting x = 0 in equations (ii) we get:
⇒ 6 x 0 + 2y = 16
⇒ y = 8
x = 0, y = 8
Putting y = 0 in equation (ii), we get:
⇒ 6x + 2 x 0 = 16
⇒ x = 8/3
x = 8/3, y = 0
Use the following table to draw the graph.

Draw the graph by plotting the two points C(0,8), D(8/3,0) from table.
Thus the graph of the two equations coincide
Consequently, every solution of one equation is a solution of the other.
Hence the equations have infinitely many solutions.
Q.14. Show graphically that each one of the following systems of equations has infinitely many solutions:
x − 2y + 11 = 0
3x − 6y + 33 = 0
Ans. The given equations are
x − 2y + 11 = 0 ...(i)
3x − 6y + 33 = 0 ...(ii)
Putting x = 0 in equation (i), we get:
⇒ 0 - 2y = -11
⇒ y = 11/2
x = 0, y = 11/2
Putting y = 0 in equation (i), we get:
⇒ x - 2x = -11
⇒ x = -11
x = -11, y = 0
Use the following table to draw the graph.

Draw the graph by plotting the two points A(0,11/2),(-11,0) from table.

Graph of the equation….(ii):
3x - 6y = -33….(ii)
Putting x = 0 in equation (ii) we get:
⇒ 3 x 0 - 6y = -33
⇒ y = 11/2
x = 0, y = 11/2
Putting y = 0 in equation (ii), we get
⇒ 3x - 6 x 0 = -33
⇒ x = -11
x = -11, y = 0
Draw the graph by plotting the two points C(0,11/2),D(-11,0) from table.
Thus the graph of the two equations are coincide
Consequently, every solution of one equation is a solution of the other.
Hence the equations have infinitely many solutions.
Q.15. Show graphically that each one of the following systems of equations is in-consistent (i.e. has no solution) :
3x − 5y = 20
6x − 10y = −40
Ans. The given equations are
3x - 5y = 20 ....(i)
6x − 10y = −40 ....(ii)
Putting x = 0 in equation (i) we get:
⇒ 3 x 0 - 5y = 20
⇒ y = - 4
x = 0, y = -4
Putting y = 0 in equation (i) we get
⇒ 3x - 5 x 0 = 20
⇒ x = 20/3
x = 20/3, y = 0
Use the following table to draw the graph.

Draw the graph by plotting the two points A(0,-4), B(20/3,0) from table.

Graph of the equation ...(ii):
6x - 10y = -4 ...(ii)
Putting x = 0 in equation (ii) we get:
⇒ 6 x 0 - 10y = -4
⇒ y = 2/5
x = 2/5, y = 0
Putting y = 0 in equation (ii) we get:
⇒ 6x - 10 x 0 = -4
⇒ x = -2/3
x = -2/3, y = 0
Use the following table to draw the graph.

Draw the graph by plotting the two points C(0,-4), D(20/3,0) from table.
Here we see that the two lines are parallel
Hence the given system of equations has no solution.
Q.16. Show graphically that each one of the following systems of equations is in-consistent (i.e. has no solution) :
x − 2y = 6
3x − 6y = 0
Ans. The given equations are
x − 2y = 6 ...(i)
3x − 6y = 0 ...(ii)
Putting x = 0 in equation (i), we get:
⇒ 0 - 2y = 6
⇒ y = -3
⇒ x = 0, y = -3
Putting y = 0 in equation (i) we get:
⇒ x- 2 x 0 = 6
⇒ x = 6
⇒ x = 6, y = 0
Use the following table to draw the graph.

The graph of (i) can be obtained by plotting the two points A(0,-3), B(6,0)
Graph of the equation….(ii):
3x - 6y = 0 ….(ii)
Putting x = 0 in equation (ii) we get:
⇒ 3 x 0 - 6y = 0
⇒ y = 0
⇒ x = 0, y = 0
Putting y = 1 in equation (ii), we get:
⇒ 3x - 6 x 1 = 0
⇒ x = 2
⇒ x = 2, y = 1
Use the following table to draw the graph.

Draw the graph by plotting the two points C(0,0)D(2,1) from table.

Here the two lines are parallel and so there is no point in common
Hence the given system of equations has no solution.
Q.17. Show graphically that each one of the following systems of equations is in-consistent (i.e. has no solution) :
2y − x = 9
6y − 3x = 21
Ans. The given equations are
2y - x = 9 ....(i)
6y − 3x = 21 ....(ii)
Putting x = 0 in equation (i), we get:
⇒ 2y - 0 = 9
⇒ y = 9/2
⇒ x = 0, y = 9/2
Putting y = 0 in equation (i) we get:
⇒ 2x - x = 9
⇒ x = -9
⇒ x = -9, y = 0
Use the following table to draw the graph.

Draw the graph by plotting the two points A(0,9/2), B(-9,0) from table.

6y - 3x = 21 ....(ii)
Putting x = 0 in equation (ii) we get:
⇒ 6y - 3 x 0 = 21
⇒ y = 7/2
⇒ x = 0, y = 7/2
Putting y = 0 in equation (ii) we get:
⇒ 6 x 0 - 3x = 21
⇒ y = 7/2
∴ x = - 7, y = 0
Use the following table to draw the graph.

Draw the graph by plotting the two points C(0,7/2),D(-7, 0) from table.
Here two lines are parallel and so don’t have common points
Hence the given system of equations has no solution.
Q.18. Show graphically that each one of the following systems of equations is in-consistent (i.e. has no solution) :
3x − 4y − 1 = 0

Ans. The given equations are
3x - 4y - 1 = 0 ....(i)

6x - 8y + 15 = 0 ....(ii)
Putting x = 0 in equation (i), we get:
⇒ 3 x 0 - 4y = 1
⇒ y = -1/4
⇒ x = 0, y = -1/4
Putting y = 0 in equation (i), we get:
⇒ 3x - 4 x 0 = 1
⇒ x = 1/3
⇒ x = 1/3, y = 0
Use the following table to draw the graph.

The graph of (i) can be obtained by plotting the two points A(0, -1/4), B(1/3,0).
6x - 8y = - 15 ....(ii)
Putting x = 0 in equation we (ii) get:
⇒ 6 x 0 - 8y = - 15
⇒ y = 15/8
⇒ x = 0, y = 15/8
Putting y = 0 in equation (ii), we get:
⇒ 6x - 8 x 0 = - 15
⇒ x = - 15/6
⇒ x = -5/2, y = 0
Use the following table to draw the graph.

Draw the graph by plotting the two points C(0,15/8), D(-5/2,0) from table.

Here, the two lines are parallel.
Hence the given system of equations is inconsistent.