Chapter 4 - Quadratic Equations, RD Sharma Solutions - (Part - 4) | RD Sharma Solutions for Class 10 Mathematics PDF Download
Page No 4.32
Q.3. Solve for x:
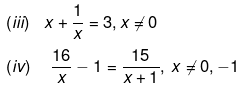

Ans.
(i) We have been given,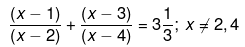
Now we solve the above equation as follows,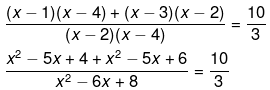
6x2 - 30x + 30 = 10x2 - 60x + 80
4x2 - 30x + 50 = 0
2x2 - 15x + 25 = 0
Now we also know that for an equation ax2 + bx + c = 0, the discriminant is given by the following equation:
D = b2 - 4ac
Now, according to the equation given to us, we have,a = 2, b = -15 and c = 25.
Therefore, the discriminant is given as,
D = (-15)2 - 4(2)(25)
= 225 - 200
= 25
Now, the roots of an equation is given by the following equation,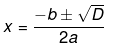
Therefore, the roots of the equation are given as follows,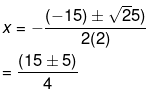
Now we solve both cases for the two values of x. So, we have,
x=(15+5)/4
= 5
Also,
x=(15-5)/4
=5/2
Therefore, the value of x = 5, 5/2.
(ii) We have been given,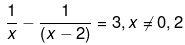
Now we solve the above equation as follows,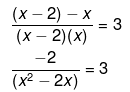
-2 = 3x2 - 6x
3x2 - 6x + 2 = 0
Now we also know that for an equation ax2 + bx + c = 0, the discriminant is given by the following equation:
D = b2 - 4ac
Now, according to the equation given to us, we have, a = 3, b = -6 and c = 2.
Therefore, the discriminant is given as,
D = (-6)2 - 4(3)(2)
= 36 - 24
= 12
Now, the roots of an equation is given by the following equation,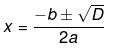
Therefore, the roots of the equation are given as follows,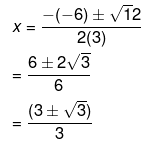
Now we solve both cases for the two values of x. So, we have,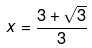
Also,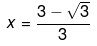
Therefore, the value of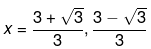
(iii) We have been given,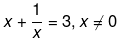
Now, we solve the equation as follows: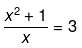
x2 + 1 = 3x
x2 - 3x + 1 = 0
Now we also know that for an equation ax2 + bx + c = 0, the discriminant is given by the following equation:
D = b2 - 4ac
Now, according to the equation given to us, we have, a = 1, b = -3 and c = 1.
Therefore, the discriminant is given as,
D = (-3)2 - 4(1)(1)
= 9 - 4
= 5
Now, the roots of an equation is given by the following equation,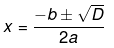
Therefore, the roots of the equation are given as follows,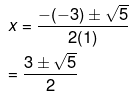
Now we solve both cases for the two values of x. So, we have,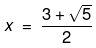
Also,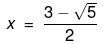
Therefore, the value of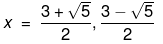
(iv) We have been given,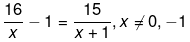
Now we solve the above equation as follows,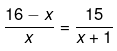
⇒ (16−x)(x+1)=15x
⇒ 16x+16−x2−x=15x
⇒ 15x+16−x2−15x=0
⇒ 16−x2=0
⇒ x2−16=0
Now we also know that for an equation ax2 + bx + c = 0, the discriminant is given by the following equation:
D = b2 - 4ac
Now, according to the equation given to us, we have, a = 1, b = -3 and c = 1.
Therefore, the discriminant is given as,
D=(0)2−4(1)(−16)
= 64
Now, the roots of an equation is given by the following equation,
Therefore, the roots of the equation are given as follows,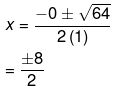
= ± 4
Therefore, the value of x = ± 4
(v) We have been given,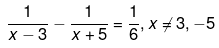
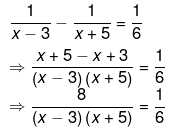
⇒ 48=x2+2x−15
⇒ x2+2x−15−48 = 0
⇒ x2+2x−63=0
⇒ x2+9x−7x−63 = 0
⇒ x(x+9)−7(x+9) = 0
⇒ (x−7)(x+9) = 0
⇒ x = 7, −9
Page No 4.4
Q.1. Which of the following are quadratic equations?
(i) x2 + 6x − 4 = 0
(ii) √3x2 - 2x + 1/2 = 0
(iii) x2 + 1/x2 = 5
(iv) x - 3/x = x2
(v) 2x2 - √3x + 9 = 0
(vi) x2 - 2x - √x - 5 = 0
(vii) 3x2 - 5x + 9 = x2 - 7x + 3
(viii) x + 1/x = 1
(ix) x2 - 3x = 0
(x) (x + 1/x)2 = 3 (x + 1/x) + 4
(xi) (2x+1) (3x+2) = 6(x-1)(x-2)
(xii) x + 1/x = x2, x ≠ 0
(xiii) 16x2 − 3 = (2x + 5) (5x − 3)
(xiv) (x + 2)3 = x3 − 4
(xv) x(x + 1) + 8 = (x + 2) (x − 2)
Ans.
(i) Here it has been given that,
x2 + 6x - 4 = 0
Now, the above equation clearly represents a quadratic equation of the form ax2 + bx + c = 0, where a = 1, b = 6 and c = -4.
Hence, the above equation is a quadratic equation.
(ii) Here it has been given that,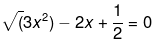
Now, solving the above equation further we get,

Now, the above equation clearly represents a quadratic equation of the form ax2 + bx + c = 0, where a = 2√3, b = -4 and c = 1.
Hence, the above equation is a quadratic equation.
(iii) Here it has been given that,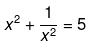
Now, solving the above equation further we get,
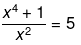
⇒ x4 + 1 = 5x2
⇒ x4 − 5x2 + 1 = 0
Now, the above equation clearly does not represent a quadratic equation of the form ax2 + bx + c = 0, because x4 − 5x2 + 1 = 0 is a polynomial of degree 4.
Hence, the above equation is not a quadratic equation.
(iv) Here it has been given that,
Here it has been given that,
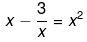
Now, solving the above equation further we get,
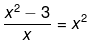
x2 - 3 = x3
-x3 + x2 - 3 = 0
Now, the above equation clearly does not represent a quadratic equation of the form ax2 + bx + c = 0, because -x3 + x2 - 3 = 0 is a polynomial of degree 3.
Hence, the above equation is not a quadratic equation.
(v) Here it has been given that,
2x2 - √3x + 9 = 0
Now, the above equation clearly does not represent a quadratic equation of the form ax2 + bx + c = 0, because 2x2-√3x+9=0 contains a term x1/2, where 1/2 is not an integer.
Hence, the above equation is not a quadratic equation.
(vi) Here it has been given that,
x2 - 2x - √x - 5 = 0
Now, the above equation clearly does not represent a quadratic equation of the form ax2 + bx + c = 0, because x2 - 2x - √x - 5 = 0 contains an extra term x1/2, where 1/2 is not an integer.
Hence, the above equation is not a quadratic equation.
(vii) Here it has been given that,
3x2 - 5x + 9 = x2 - 7x + 3
Now, after solving the above equation further we get,
2x2+2x+6 = 0
x2 +x +3 = 0
Now, the above equation clearly does not represent a quadratic equation of the form ax2 + bx + c = 0, where a = 1, b = 1 and c = 3. Hence, the above equation is a quadratic equation.
(viii) Here it has been given that,
x + 1/x = 1
Now, solving the above equation further we get,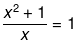
x2 + 1 = x
x2 - x + 1 = 0
Now as we can see, the above equation clearly represents a quadratic equation of the form ax2 + bx + c = 0, where a = 1, b = -1 and c = 1.
Hence, the above equation is a quadratic equation.
(ix) Here it has been given that,
x2 - 3x = 0
Now as we can see, the above equation clearly represents a quadratic equation of the form ax2 + bx + c = 0, where a = 1, b = -3 and c = 0.
Hence, the above equation is a quadratic equation.
(x) Here it has been given that,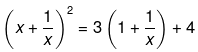
Now, solving the above equation further we get,
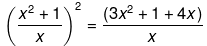
Now as we can see, the above equation clearly does not represent a quadratic equation of the form ax2 + bx + c = 0, because x4 - 3x3 - 2x2 - x + 1 is a polynomial having a degree of 4 which is never present in a quadratic polynomial.
Hence, the above equation is not a quadratic equation.
(xi) Here it has been given that,
(2x+1) (3x+2) = 6(x-1)(x-2)
Now, after solving the above equation further we get,
6x2 +7x+ 2 =6x2-18x+12
25x-10=0
5x-2=0
Now as we can see, the above equation clearly does not represent a quadratic equation of the form ax2 + bx + c = 0, because 5x - 2 = 0 is a linear equation.
Hence, the above equation is not a quadratic equation.
(xii) Here it has been given that,
Now, solving the above equation further we get,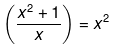
x2+1 = 0
-x3+x2+1 = 0
Now as we can see, the above equation clearly does not represent a quadratic equation of the form ax2 + bx + c = 0, because -x3+x2+1 = 0 is a polynomial having a degree of 3 which is never present in a quadratic polynomial.
Hence, the above equation is not a quadratic equation.
(xiii) Here it has been given that,
16x2 − 3 = (2x + 5) (5x − 3)
Now, after solving the above equation further we get,
16x2-3 = 10x2 + 19x - 15
4x2 - 19x + 12 = 0
Now as we can see, the above equation clearly represents a quadratic equation of the form ax2 + bx + c = 0, where a = 4, b = -19 and c = 12. Hence, the above equation is a quadratic equation.
(xiv) Here it has been given that,
(x + 2)3 = x3 − 4
Now, after solving the above equation further we get,
x3 +8 + 3(x)(2)(x+ 2) = x3 -4
12+6x2 +12x = 0
x2 + 2x + 2 = 0
Now as we can see, the above equation clearly represents a quadratic equation of the form ax2 + bx + c = 0, where a= 1, b = 2 and c = 2.
Hence, the above equation is a quadratic equation.
(xv) Here it has been given that,
x(x + 1) + 8 = (x + 2) (x − 2)
Now, solving the above equation further we get,
x2+x+8 = x2 - 4
x+12 = 0
Now as we can see, the above equation clearly does not represent a quadratic equation of the form ax2 + bx + c = 0, because x+12 = 0 is a linear equation which does not have a x2 term in it.
Q.2. In each of the following, determine whether the given values are solutions of the given equation or not:
(i) x2−3x+2=0, x=2, x=−1
(ii) x2+x+1=0, x=0, x=1
(iii) x2−3√3x+6=0, x=√3, x=−2√3
(iv) x+1/x=13/6, x=5/6, x=4/3
(v) 2x2−x+9=x2+4x+3, x=2, x=3
(vi) x2−√2x−4=0, x=−√2, x=−2√2
(vii) a2x2−3abx+2b2=0, x=a/b, x=b/a
Ans.
We are given the following quadratic equations and we are asked to find whether the given values are solutions or not
(i) We have been given that,
x2−3x+2=0, x=2, x=−1
Now if x = 2 is a solution of the equation then it should satisfy the equation
So, substituting x = 2 in the equation we get
x2 -3x + 2 = (2)2 -3(2) + 2
= 4 - 6 + 2
= 0
Hence, x = 2 is a solution of the given quadratic equation.
Also, if x = -1 is a solution of the equation then it should satisfy the equation
So, substituting x = -1 in the equation, we get
x2 - 3x+3 = (-1)2 - 3(-1) + 2
= 1 + 3+2
=6
Hence x = -1 is not a solution of the quadratic equation
Therefore, from the above results we find out that x = 2 is a solution and x = -1 is not a solution of the given quadratic equation.
(ii) We have been given that,
x2+x+1=0, x=0, x=1
Now if x = 0 is a solution of the equation then it should satisfy the equation.
So, substituting x = 0 in the equation, we get
x2+x+1 = (0)2 + (1) + 1
= 1
Hence x = 0 is not a solution of the given quadratic equation.
Also, if x =1 is a solution of the equation then it should satisfy the equation.
So, substituting x = 0, in the equation, we get
x2+x+1 = (1)2 + (1) + 1
= 3
Hence x = 3 is not a solution of the quadratic equation.
Therefore, from the above results we find out that both x = 0 and x = -1 are not a solution of the given quadratic equation.
FAQs on Chapter 4 - Quadratic Equations, RD Sharma Solutions - (Part - 4) - RD Sharma Solutions for Class 10 Mathematics
| 1. What is the general form of a quadratic equation? |  |
| 2. How many solutions can a quadratic equation have? |  |
| 3. What is the discriminant of a quadratic equation? |  |
| 4. How can you solve a quadratic equation using the quadratic formula? |  |
| 5. What is the sum of the roots of a quadratic equation? |  |

|
Explore Courses for Class 10 exam
|

|

















