Chapter 6 - Triangles, RD Sharma Solutions - (Part - 2) | RD Sharma Solutions for Class 10 Mathematics PDF Download

Page No 7.119

Q.11. ABCD is a square. F is the mid-point of AB. BE is one third of BC. If the area of ∆FBE = 108 cm², find the length of AC.
Ans.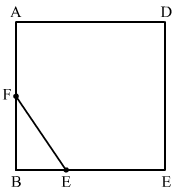 
It is given that F is the midpoint of AB. Therefore, we have AF = FB.
It is also given that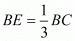.....(1)
Now look at the figure. Quadrilateral ABCD is a square and hence all angles are of 90º.
In ΔFBE, ∠B = 90° and hence it is a right angle triangle.
We know that the area of the right angle triangle is 1/2 × base × height
Therefore, Ar(ΔFBE) = 1/2 × BF × BE
= 108 cm²
Now we will multiple both sides of the equation by 2 we get, BF x BE = 216 .....(2)
But we know that and.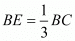
Let us substitute these values in equation (2) we get,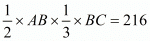

Let us simplify the above equation as below,
AB x BC = 6 x 216
But we know that ABCD is a square and hence AB = BC = CD = AD.
∴ AB² = 6 x 216 .....(3)
We know that 216 is the cube of 6 therefore we can write the equation (3) as below,
AB² = 6³ × 6
AB² = 6⁴
∴ AB = 6² = 36
Therefore, side of the square ABCD is 36 cm.
Now we are going to find the diagonal AC.
Diagonal of the square can be calculate by using the formula given below,
Diagonal = 2 Side
AC = √2 x 36 .....(4)
We know that √2 = 1.414
Let us substitute the value of √2 in equation (3).
AC = 1.414 x 36
= 50.904
Therefore, the length of AC is 50.904 cm.

Q.12. In an isosceles triangle ABC, if AB = AC = 13 cm and the altitude from A on BC is 5 cm, find BC.
Ans.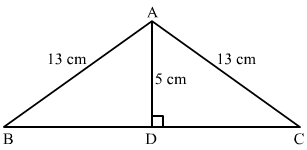 
We have given an isosceles triangle and we know that the altitude drawn on the unequal side of the isosceles triangle bisects that side.
Therefore, in ΔADB and ΔADC
∠B=∠C (Equal sides have equal angles opposite to them)
AD = AD
∠ADB = ∠ADC (90° each)
ΔADB ≅ ΔADC (AAS congruence theorem)
∴ BD = DC
Now we will use Pythagoras theorem in right angled triangle ADB.
AB² = AD² + BD²
Let us substitute the values of AB and AD we get, 13² = 5² + BD²
169 = 25 + BD²
Subtracting 25 from both sides we get,
BD² = 169 - 25
BD² = 144
∴ BD = 12
Since BC = 2BD
∴ BC = 2 x 12
= 24
Therefore, length of BC is 24 cm.

Q.13. In a ∆ABC, AB = BC = CA = 2a and AD ⊥ BC. Prove that
(i) AD = a√ 3
(ii) Area (ΔABC) = √3a²
Ans.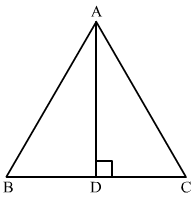 
In ΔADB and ΔADC
∠B = ∠C (60º each)
AD = AD
∠ADB = ∠ADC (90º each)
ΔADB ≅ ΔADC (AAS congruence theorem)
∴ BD = DC
∴ BC = 2BD
But BC = 2a therefore, we get,
2a = 2 BD ………(1)
Now we will divide both sides of the equation (1) by 2, we get,
∴ BD = a
Now we will use Pythagoras theorem in right angled triangle ADB.
AB² = AD² + BD²
Now we will substitute the values of AB and BD we get,
(2a)² = AD² + a²
4a² = AD² + a²
3a² = AD²
∴ AD = √3a
Therefore, AD = √3a.
We have given an equilateral triangle and we know that the area of the equilateral triangle is.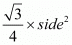
Here, side is 2a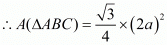


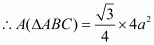
A(ΔABC) = √3a²
Therefore, A(ΔABC) = √3a².

Q.14. The lengths of the diagonals of a rhombus are 24 cm and 10 cm. Find each side of the rhombus.
Ans. We know that a quadrilateral is said to a rhombus if all sides of the quadrilateral are equal. Diagonals of a rhombus bisect each other at right angles.
Quadrilateral ABCD is a rhombus and diagonals AC and BD intersect at point O.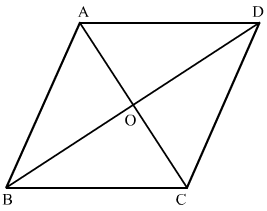
As we defined above, we get AB = BC = CD = AD, AO = OC, BO = OD and angle ∠AOD = ∠AOB = ∠BOC = ∠COD = 90°.
We are given that AC = 10 cm and BD = 24 cm.
Therefore, we get, AO = OC = 5 cm and BO = OD = 12 cm.
Now we will use Pythagoras theorem in the right angled triangle AOD as below,
AD² = AO² + OD² …......(1)
Now we will substitute the values of AO and OD in equation (1) we get,
AD² = 5² + 12²
AD² = 25 + 144
AD² = 169
Let us take the square root
AD = 13
Therefore, length of the side of the rhombus is 13 cm.

Q.15. Each side of a rhombus is 10 cm. If one its diagonals is 16 cm find the length of the other diagonal.
Ans. We know that a quadrilateral is said to a rhombus if all sides of the quadrilateral are equal. Diagonals of a rhombus bisect each other at right angles.Quadrilateral ABCD is a rhombus and diagonals AC and BD intersect at point O.
As we defined above, we get AB = BC = CD = AD, AO = OC, BO = OD and angle ∠AOD = ∠AOB = ∠BOC = ∠COD = 90°.
We are given that AB = 10 cm and AC = 16 cm. Now we will find length of BD.
As we know the definition of rhombus we get AB = BC = CD = AD.
Therefore, we get, AB = BC = CD = AD = 10 cm
Also we know that diagonals of rhombus bisect each other at right angles therefore, we get,
AO = OC,
BO = OD
and ∠AOD = ∠AOB = ∠BOC = ∠COD = 90°
Here, we know the length of AC therefore, we get, AO = OC = 8 cm .
Now we will use Pythagoras theorem in the right angled triangle AOD as below,
AD² = AO² + OD² …......(1)
Now we will substitute the values of AD and AO in equation (1) we get,
10² = 8² + OD²
100 = 64 + OD²…......(2)
Now we will subtract 64 from both sides of the equation (2)
OD² = 100 - 64
OD² = 36
Now we will take the square root.
OD = 6
We know that BD = 20D
∴ BD = 2 x 6

∴ BD = 12
Therefore, length of the other diagonal is 12 cm.

Q.16. Calculate the height of an equilateral triangle each of whose sides measures 12 cm.
Ans. We are asked to find the height of the equilateral triangle.
Let us draw the figure. Let us draw the altitude AD. We know that altitude is also median of the equilateral triangle.
Therefore, BD = DC = 6 cm.
In right angled triangle ADB, we will Pythagoras theorem, as shown below,
AB² = AD² + BD² 
Now we will substitute the values.
12² = AD² + 6²
144 = AD²  + 36
AD² = 144 − 36 = 108

Taking square root, we get
AD = 10.39 cm
Therefore, the height of the equilateral triangle is 10.39 cm.

Q.17. In the given figure, ∠B < 90° and segment AD ⊥ BC, show that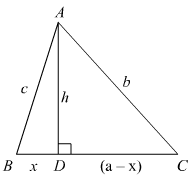
(i) b² = h² + a² + x² − 2ax
(ii) b² = a² + c² − 2 ax
Ans. (i) Since AD perpendicular to BC we obtained two right angled triangles, triangle ADB and triangle ADC.
We will use Pythagoras theorem in the right angled triangle ADC
AC² = AD² + DC² …......(1)
Let us substitute AD = h, AC = b and DC = (a − x) in equation (1) we get,
b² = h² + (a - x)²
b² = h² + a² - 2ax + x²
b² = h² + a² + x² - 2ax …......(2)
(ii) Let us use Pythagoras theorem in the right angled triangle ADB as shown below,
AB² = AD² + BD² …......(3)
Let us substitute AB = c, AD = h and BD = x in equation (3) we get,
c² = h² + x²
Let us rewrite the equation (2) as below,
b² = h² + a² + x² - 2ax …......(4)
Now we will substitute h² + x² = c² in equation (4) we get,
b² = c² + a² - 2ax
Therefore, b² = c² + a² - 2ax.

Q.18. In an equilateral ∆ABC, AD ⊥ BC prove that AD² = 3BD².
Ans.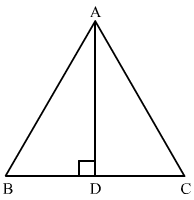 
We have to prove that AD² = 3BD² .
In right angled ∆ABC, using Pythagoras theorem we get,
AB² = AD² + BD²….....(1)
We know that in an equilateral triangle every altitude is also median.
Therefore, AD bisects BC.
Therefore, we have BD = DC
Since ∆ABC is an equilateral triangle, AB = BC = AC
Therefore, we can write equation (1) as
BC² = AD² + BD²…......(2)
But BC = 2BD
Therefore, equation (2) becomes,
(2BD)² = AD² + BD²
Simplifying the equation we get,
4BD² - BD^{2 =} AD²
3BD² = AD²
Therefore, AD² = 3BD².

Page No 7.120

Q.19. ∆ABD is a right triangle right-angled at A and AC ⊥ BD. Show that
(i) AB² = BC . BD
Ans.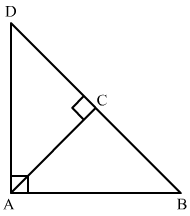 
In ∆ABD and ∆ABC,
∠ACB = ∠A = 90°
∠B = ∠B (Common angle)
So, by AA criterion ∆ABD ∼ ∆CBA
∴ AB/BC = BD/AB = AD/AC
∴ AB/BC = BD/AB
∴ AB² = BD.BC .....(1)

(ii) AC² = BC . DC
Ans. In ∆ABD and ∆ACD,
∠C = ∠A = 90°
∠D = ∠D (Common angle)
So, by AA criterion ∆ABD ∼ ∆CAD
∴ AB/AC = BD/AD = AD/CD
∴ BD/AD = AD/CD
∴ AD² = BD . CD .....(2)

(iii) AD² = BD . CD
Ans. We have shown that ∆ABD is similar to ∆CBA and ∆ABD is similar to ∆CAD
therefore, by the property of transitivity ∆CBA is similar to ∆CAD.
∴ BC/AC = AB/AD = AC/CD
∴ BC/AC = AC/CD
∴ AC² = BC . CD .....(3)

(iv) AB²/AC² = BD / DC
Ans. Now to obtained AB²/AC² = BD / DC, we will divide equation (1) by equation (2) as shown below,
∴ AB²/AC² = BD . BC/BC . CD
Canceling BC we get,
 AB²/AC² = BD/CD
Therefore, AB²/AC² = BD/CD.

Q.20. A guy wire attached to a vertical pole of height 18 m is 24 m long has a stake attached to the other end. How far from the base of pole should the stake be driven so that the wire will be taut?
Ans. We will draw the figure from the given information as below,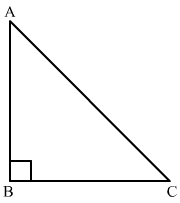
Let AB be the vertical pole of length 18 m and let the stake be at the point C so the wire will be taut.
Therefore, we have AB = 18 m, AC = 24 m and we have to find BC.
Now we will use Pythagoras theorem,
AC² = AB² + BC²
Let us substitute the values we get,
24² = 18² + BC²
576 = 324 + BC²
Subtracting 324 from both sides of the equation we get,
BC² = 576 - 324
BC² = 252
We can rewrite the 252 as 36 x 7, therefore, our equation becomes, BC² = 36 x 7
Now we will take the square root,
BC = 6 x √7
Therefore, the stake should be 6√7 far from the base of the pole so that the wire will be taut.