Chapter 3 - Pair Of Linear Equations In Two Variables, RD Sharma Solutions - (Part-14) | RD Sharma Solutions for Class 10 Mathematics PDF Download

Page No 3.47

Q.53. Write a pair of linear equations which has the unique solution x = −1 , y = 3 .How many such  pairs can you write ?
Ans. The unique solution is given as x = −1 and y = 3.
The one pair of linear equations having x = −1 and y = 3 as unique solution can be
12x + 5y = 3
2x + y = 1
Similarly, infinitely many pairs of linear equations are possible.

Page No 3.57

Q.1. Solve each of the following systems of equations by the method of cross-multiplication :
x + 2y + 1 = 0
2x − 3y − 12 = 0
Ans. GIVEN:
x + 2y + 1 = 0
2x − 3y − 12 = 0
To find: The solution of the systems of equation by the method of cross-multiplication:
By cross multiplication method we get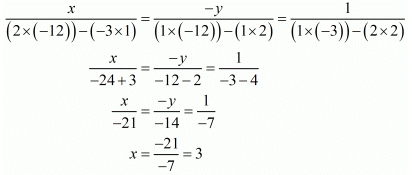

and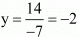
Hence we get the value of x = 3 and y = - 2

Q.2. Solve each of the following systems of equations by the method of cross-multiplication :
3x + 2y + 25 = 0
2x + y + 10 = 0
Ans.
GIVEN:
3x + 2y + 25 = 0
2x + y + 10 = 0
To find: The solution of the systems of equation by the method of cross-multiplication:
By cross multiplication method we get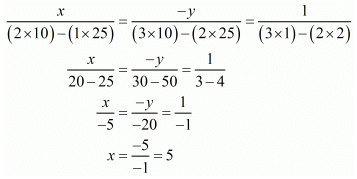

Also
Hence we get the value of x = 5 and y = - 20

Q.3. Solve each of the following systems of equations by the method of cross-multiplication :
2x + y = 35
3x + 4y = 65
Ans.
GIVEN:
2x + y = 35
3x + 4y = 65
To find: The solution of the systems of equation by the method of cross-multiplication:
Here we have the pair of simultaneous equation
2x + y = 35
3x + 4y = 65
By cross multiplication method we get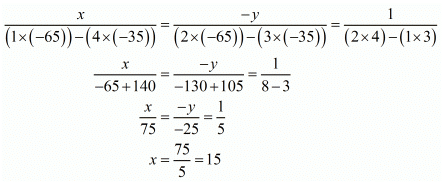

Also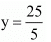
Hence we get the value of x = 15 and y = 5

Q.4. Solve each of the following systems of equations by the method of cross-multiplication :
2x − y = 6
x − y = 2
Ans. GIVEN:
2x − y = 6
x − y = 2
To find: The solution of the systems of equation by the method of cross-multiplication:
Here we have the pair of simultaneous equation
2x - y - 6 = 0
x - y - 2 = 0
By cross multiplication method we get

Hence we get the value of x = 4 and y = 2.

Q.5. Solve each of the following systems of equations by the method of cross-multiplication: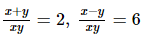

Ans.
GIVEN: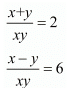

To find: The solution of the systems of equation by the method of cross-multiplication:
Here we have the pair of simultaneous equation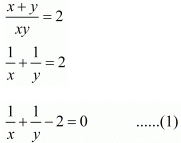


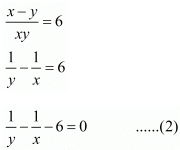
Let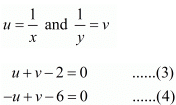

By cross multiplication method we get


We know that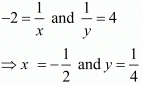

Hence we get the value of

Q.6. Solve each of the following systems of equations by the method of cross-multiplication :
ax + by = a − b
bx − ay = a + b
Ans. GIVEN:
ax + by = a - b
 bx - ay = a + b
To find: The solution of the systems of equation by the method of cross-multiplication:
Here we have the pair of simultaneous equation
ax + by - (a - b) = 0
bx - ay - (a + b) = 0
By cross multiplication method we get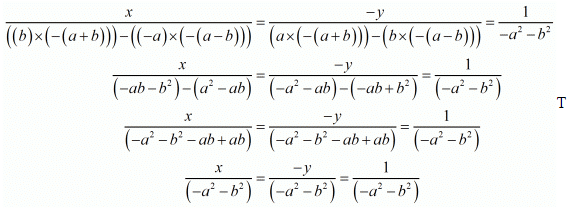

Therefore x = 1 and y = - 1
Hence we get the value of x = 1 and y = -1

Q.7. Solve each of the following systems of equations by the method of cross-multiplication :
x + ay = b
ax − by = c
Ans. GIVEN:
x + ay = b
ax − by = c
To find: The solution of the systems of equation by the method of cross-multiplication:
Here we have the pair of simultaneous equation
x + ay = b
ax − by = c
By cross multiplication method we get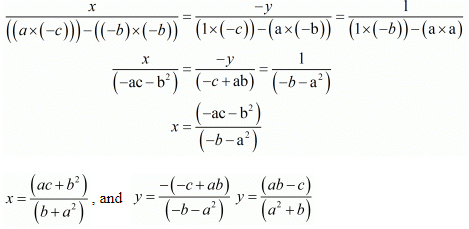

Hence we get the value of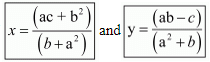

Q.8. Solve each of the following systems of equations by the method of cross-multiplication :
ax + by = a²
bx + ay = b²
Ans.
ax + by = a²
bx + ay = b²
To find: The solution of the systems of equation by the method of cross-multiplication:
Here we have the pair of simultaneous equation
ax + by = a²
bx + ay = b²
To find: The solution of the systems of equation by the method of cross-multiplication:
Here we have the pair of simultaneous equation
ax + by - a² = 0
bx + ay - b² = 0
By cross multiplication method we get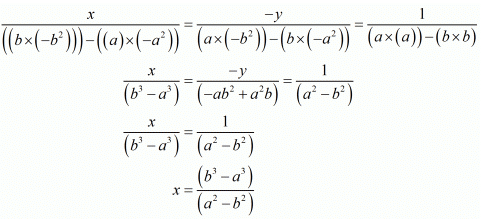


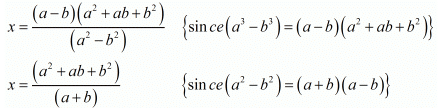
and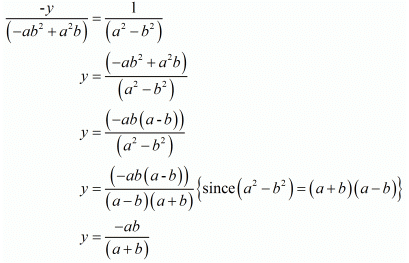

Hence we get the value of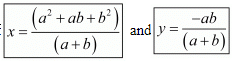

Page No 3.57

Q.9. Solve each of the following systems of equations by the method of cross-multiplication :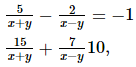

where x ≠ 0 and y ≠ 0
Ans.

To find: The solution of the systems of equation by the method of cross-multiplication:
Here we have the pair of simultaneous equation
Rewriting the equation again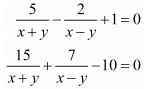


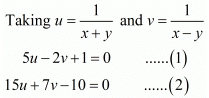
By cross multiplication method we get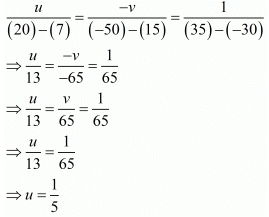

And

We know that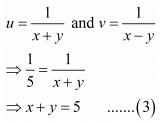

and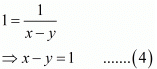

Adding equation (3) and (4)
2x = 6
x = 3
Substituting value of x in equation (3) we get
y = 5 - 3
= 2
Hence we get the value of x = 3 and y = 2

Q.10. Solve each of the following systems of equations by the method of cross-multiplication :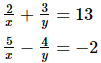

where x ≠ 0 and y ≠ 0
Ans. GIVEN: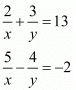

To find: The solution of the systems of equation by the method of cross-multiplication:
Here we have the pair of simultaneous equation
Rewriting the equation again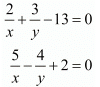


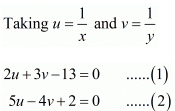
By cross multiplication method we get from eq. (1) and eq. (2)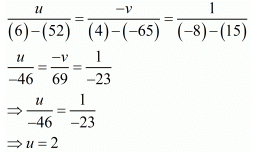

And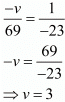

We know that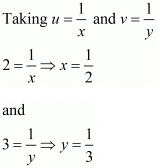

Hence we get the value of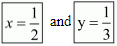

Q.11. Solve each of the following systems of equations by the method of cross-multiplication :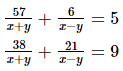

Ans.
GIVEN:

To find: The solution of the systems of equation by the method of cross-multiplication:
Here we have the pair of simultaneous equation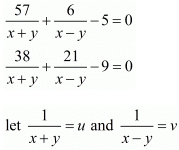

Now rewriting the given equation as
57u + 6v - 5 = 0  ...(i)
38u + 21v - 9 = 0  ...(ii)
By cross multiplication method we get

Consider the following for u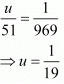

Consider the following for v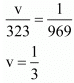

We know that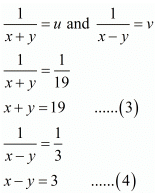

Now adding eq. (3) and (4) we get x = 11
And after substituting the value of x in eq. (4) we get y = 8
Hence we get the value of x = 11 and y = 8

Q.12. Solve each of the following systems of equations by the method of cross-multiplication :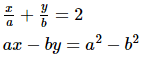

Ans. GIVEN: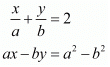

To find: The solution of the systems of equation by the method of cross-multiplication:
Here we have the pair of simultaneous equation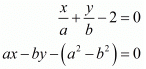

By cross multiplication method we get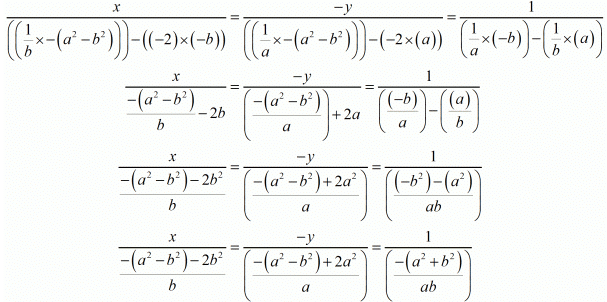

So for x we have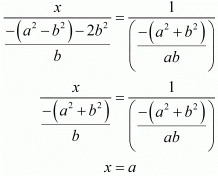

And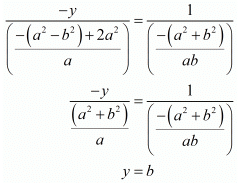

Hence we get the value of x = a and y = b

Q.13. Solve each of the following systems of equations by the method of cross-multiplication :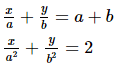

Ans. GIVEN: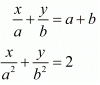

To find: The solution of the systems of equation by the method of cross-multiplication:
Here we have the pair of simultaneous equation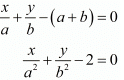

By cross multiplication method we get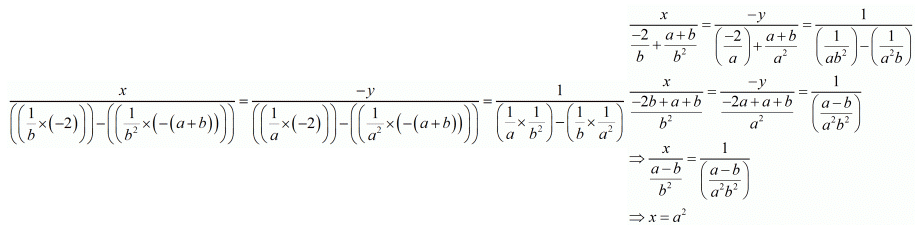

And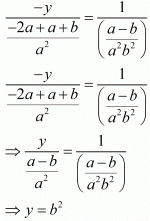

Hence we get the value of x = a² and y = b²

Page No 3.58

Q.14. Solve each of the following systems of equations by the method of cross-multiplication :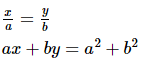

Ans. GIVEN: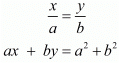

To find: The solution of the systems of equation by the method of cross-multiplication:
Here we have the pair of simultaneous equation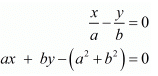

By cross multiplication method we get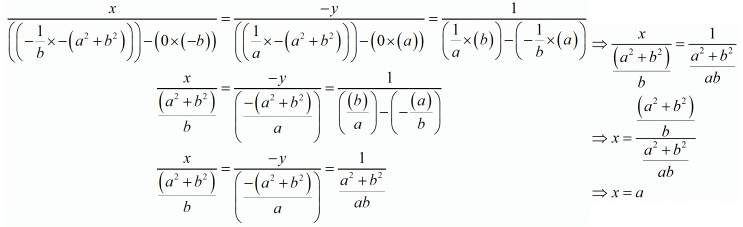

And

Hence we get the value of x = a and y = b

Q.15. Solve each of the following systems of equations by the method of cross-multiplication :
2ax + 3by = a + 2b
3ax + 2by = 2a + b
Ans.
GIVEN:
2ax + 3by = a + 2b
3ax + 2by = 2a + b
To find: The solution of the systems of equation by the method of cross-multiplication:
Here we have the pair of simultaneous equation
2ax + 3by = a + 2b
3ax + 2by = 2a + b
By cross multiplication method we get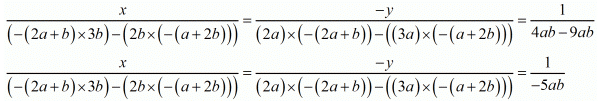

Now consider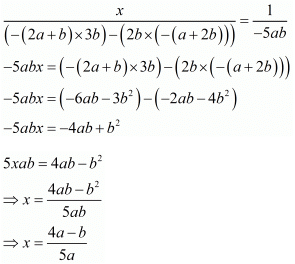

And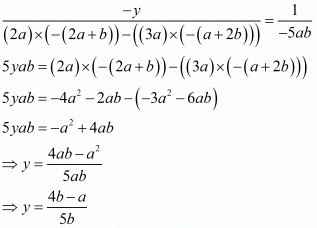

Hence we get the value of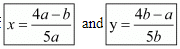

Q.16. Solve each of the following systems of equations by the method of cross-multiplication :
5ax + 6by = 28
3ax + 4by = 18
Ans. GIVEN:
5ax + 6by = 28
3ax + 4by = 18
To find: The solution of the systems of equation by the method of cross-multiplication:
Here we have the pair of simultaneous equation
5ax + 6by - 28 = 0
3ax + 4by - 18 = 0
By cross multiplication method we get

Consider the following to calculate x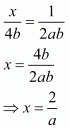

And

Hence we get the value of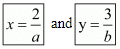

Q.17. Solve each of the following systems of equations by the method of cross-multiplication :
(a + 2b)x + (2a − b)y = 2
(a − 2b)x + (2a + b)y = 3
Ans. GIVEN:
(a + 2b)x + (2a − b)y = 2
(a − 2b)x + (2a + b)y = 3
To find: The solution of the systems of equation by the method of cross-multiplication:
Here we have the pair of simultaneous equation
(a + 2b)x + (2a − b)y - 2 = 0
(a − 2b)x + (2a + b)y - 3 = 0
By cross multiplication method we get


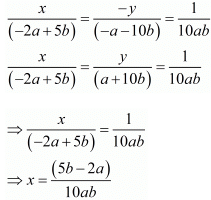
And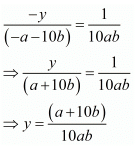

Hence we get the value of

Q.18. Solve each of the following systems of equations by the method of cross-multiplication :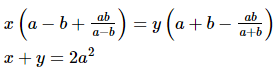

Ans.
GIVEN:

To find: The solution of the systems of equation by the method of cross
multiplication:
Here we have the pair of simultaneous equation

By cross multiplication method we get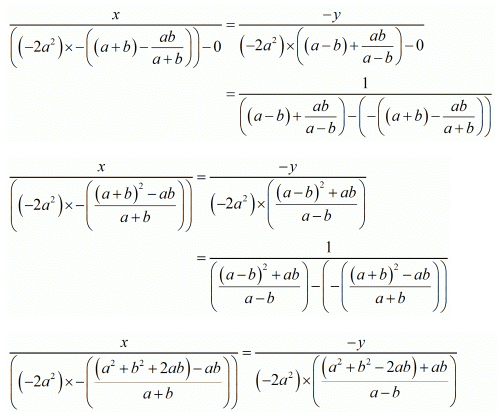



Consider the following for x

And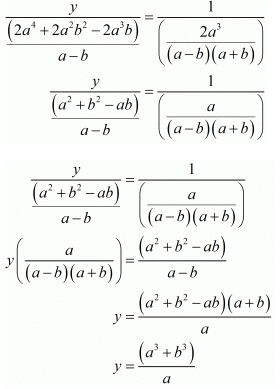

Hence we get the value of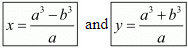

Q.19. Solve each of the following systems of equations by the method of cross-multiplication :
bx + cy = a + b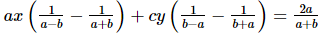

Ans. GIVEN:

To find: The solution of the systems of equation by the method of cross-multiplication:
Here we have the pair of simultaneous equation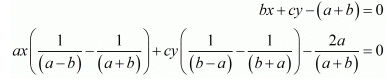

By cross multiplication method we get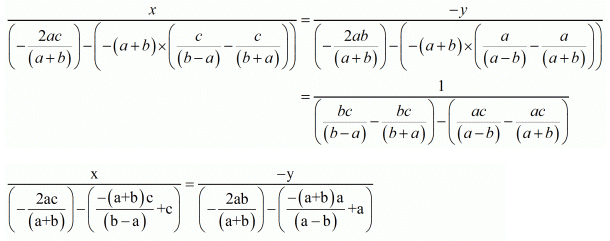

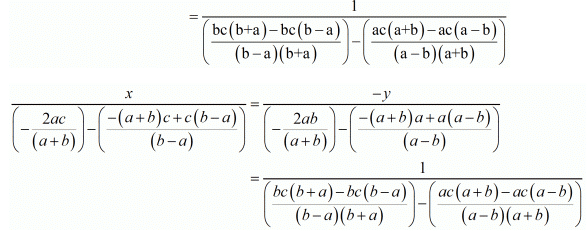
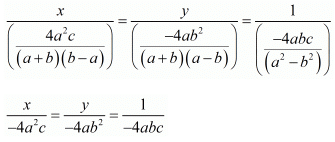
Consider the following for x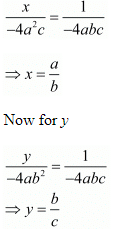

Hence we get the value of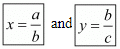

Q.20. Solve each of the following systems of equations by the method of cross-multiplication :
(a−b)x+(a+b)y=2a²−2b²
(a+b) (x+y) = 4ab
Ans.
GIVEN:
(a−b)x+(a+b)y=2a²−2b²
(a+b) (x+y) = 4ab
To find: The solution of the systems of equation by the method of cross-multiplication:
Here we have the pair of simultaneous equation
(a−b)x+(a+b)y - 2a² + 2b² = 0
(a+b) x + (a + b) y - 4ab = 0
By cross multiplication method we get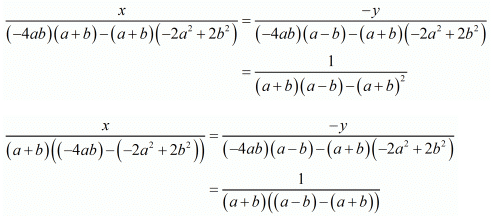

Consider the following for x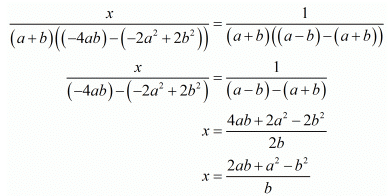

Now consider the following for y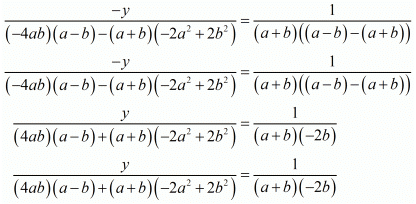


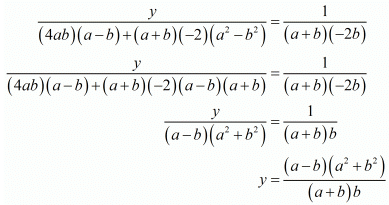
Hence we get the value of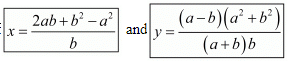

Q.21. Solve each of the following systems of equations by the method of cross-multiplication :
a²x + b² y = c²
b² x + a² y = d²
Ans.21. GIVEN:
a² x + b² y = c²
b² x + a² y = d²
To find: The solution of the systems of equation by the method of cross-multiplication:
Here we have the pair of simultaneous equation
a² x + b² y - c² = 0
b² x + a² y - d² = 0
By cross multiplication method we get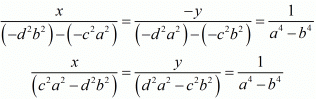

Consider the following for x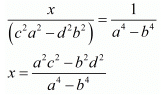

Now consider the following for y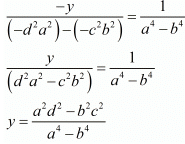

Hence we get the value of

Q.22. Solve each of the following systems of equations by the method of cross-multiplication :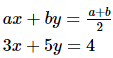

Ans.
GIVEN: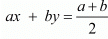

3x + 5y = 4
To find: The solution of the systems of equation by the method of cross-multiplication:
Here we have the pair of simultaneous equation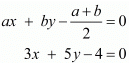

By cross multiplication method we get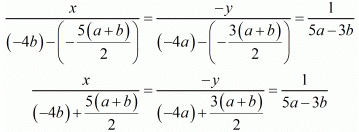


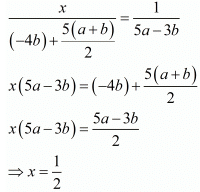
And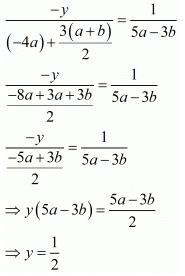

Hence we get the value of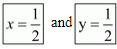

Q.23. Solve each of the following systems of equations by the method of cross-multiplication :
2(ax − by) + a + 4b = 0
2(bx + ay) + b − 4a = 0
Ans.
GIVEN:
2(ax − by) + a + 4b = 0
2(bx + ay) + b − 4a = 0
To find: The solution of the systems of equation by the method of cross-multiplication:
Here we have the pair of simultaneous equation
2(ax − by) + a + 4b = 0
2(bx + ay) + b − 4a = 0
After rewriting equations
2ax - 2by + (a + 4b) = 0
2bx + 2ay + (b - 4a) = 0
By cross multiplication method we get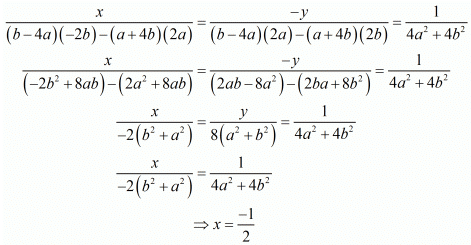

For y consider the following

Hence we get the value of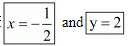

Q.24. Solve each of the following systems of equations by the method of cross-multiplication :
6(ax + by) = 3a + 2b
6(bx − ay) = 3b − 2a
Ans. GIVEN:
6(ax + by) = 3a + 2b
6(bx − ay) = 3b − 2a
To find: The solution of the systems of equation by the method of cross-multiplication:
Here we have the pair of simultaneous equation, after rewriting equations
6ax + 6by - (3a + 2b) = 0
6bx - 6ay - (3b + 2a) = 0
By cross multiplication method we get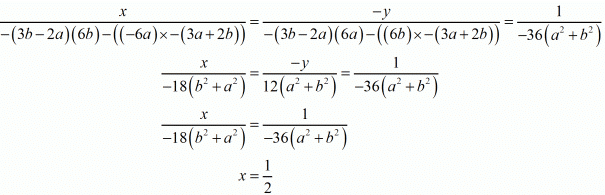

Consider the following for y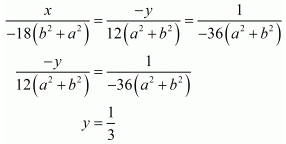

Hence we get the value of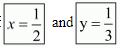

Q.25. Solve each of the following systems of equations by the method of cross-multiplication :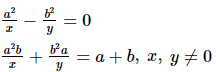

Ans. GIVEN: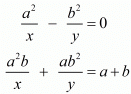
 
To find: The solution of the systems of equation by the method of cross-multiplication:
Here we have the pair of simultaneous equation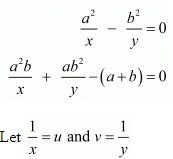

Rewriting equations
a²u - b² v = 0 .....(1)
a² bu + ab²v - (a + b) = 0 .....(2)
Now, by cross multiplication method we get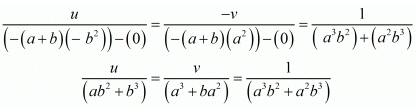

For u consider the following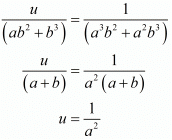

For y consider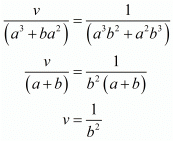

We know that

Now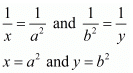

Hence we get the value of x = a² and y = b².

Q.26. Solve each of the following systems of equations by the method of cross-multiplication :
mx − ny = m² + n²
x + y = 2m
Ans.
GIVEN:
mx − ny = m² + n²
x + y = 2m
To find: The solution of the systems of equation by the method of cross-multiplication:
Here we have the pair of simultaneous equation
mx - ny - (m² + n²) = 0
x + y - 2m = 0
By cross multiplication method we get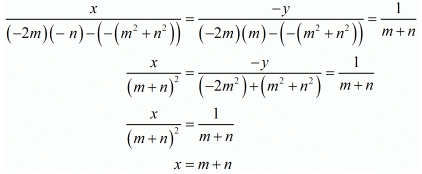

Now for y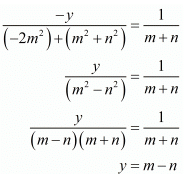

Hence we get the value of x = m + n and y = m - n