Chapter 3 - Pair Of Linear Equations In Two Variables, RD Sharma Solutions - (Part-15) | RD Sharma Solutions for Class 10 Mathematics PDF Download
Page No 3.58
Q.27. Solve each of the following systems of equations by the method of cross-multiplication :
Ans. GIVEN:
To find: The solution of the systems of equation by the method of cross-multiplication:
Here we have the pair of simultaneous equation
By cross multiplication method we get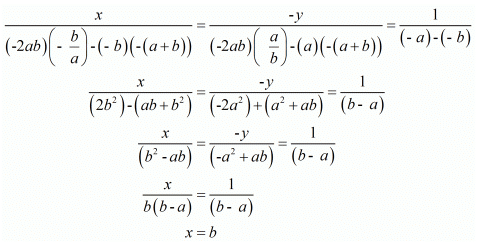
For y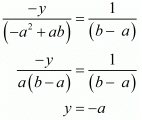
Hence we get the value of x = b and y = -a
Q.28. Solve each of the following systems of equations by the method of cross-multiplication :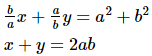
Ans. GIVEN: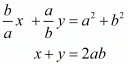
To find: The solution of the systems of equation by the method of cross-multiplication:
Here we have the pair of simultaneous equation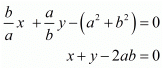
By cross multiplication method we get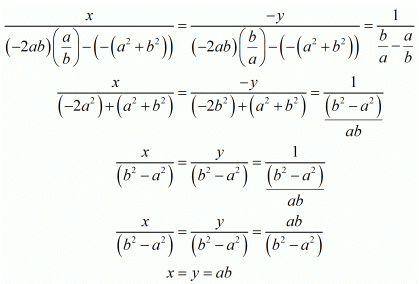
Hence we get the value of x = y = ab
Page No 3.73
Q.1. In each of the following systems of equations determine whether the system has a unique solution, no solution or infinitely many solutions. In case there is a unique solution, find it:
x − 3y = 3
3x − 9y = 2
Ans. GIVEN:
x - 3y = 3
3x - 9y = 2
To find: To determine whether the system has a unique solution, no solution or infinitely many solutions
We know that the system of equations
a1x + b1 y = c1
a2 x + b2 y = c2
For unique solution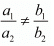
For no solution
For infinitely many solution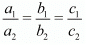
Here,
Since 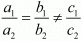 which means
which means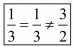 hence the system of equation has no solution.
hence the system of equation has no solution.
Hence the system of equation has no solution
Q.2. In each of the following systems of equations determine whether the system has a unique solution, no solution or infinitely many solutions. In case there is a unique solution, find it
2x + y = 5
4x + 2y = 10
Ans. GIVEN:
2x + y = 5
4x + 2y = 10
To find: To determine whether the system has a unique solution, no solution or infinitely many solutions
We know that the system of equations
a1 x + b1 y = c1
a2 x + b2y = c2
For unique solution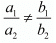
For no solution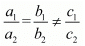
For infinitely many solution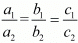
Here,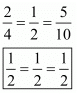
Since 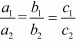 which means
which means  hence the system of equation has infinitely many solution.
hence the system of equation has infinitely many solution.
Hence the system of equation has infinitely many solutions
Q.3. In each of the following systems of equations determine whether the system has a unique solution, no solution or infinitely many solutions. In case there is a unique solution, find it
3x − 5y = 20
6x − 10y = 40
Ans. GIVEN:
3x − 5y = 20
6x − 10y = 40
To find: To determine whether the system has a unique solution, no solution or infinitely many solutions
We know that the system of equations
a1x + b1y = c1
a2x + b2y = c2
For unique solution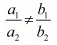
For no solution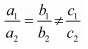
For infinitely many solution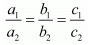
Here,
Since 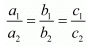 which means
which means  hence the system of equation has infinitely many solution.
hence the system of equation has infinitely many solution.
Hence the system of equation has infinitely many solutions
Q.4. In each of the following systems of equations determine whether the system has a unique solution, no solution or infinitely many solutions. In case there is a unique solution, find it
x − 2y = 8
5x − 10y = 10
Ans. GIVEN:
x − 2y = 8
5x − 10y = 10
To find: To determine whether the system has a unique solution, no solution or infinitely many solutions
We know that the system of equations
a1x + b1y = c1
a2x + b2y = c2
For unique solution
For no solution
For infinitely many solution 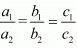
Here,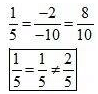
Since  which means
which means hence the system of equation has no solution.
hence the system of equation has no solution.
Hence the system of equation has no solution
Q.5. Find the value of k for which the following system of equations has a unique solution:
kx + 2y = 5
3x + y = 1
Ans.5. GIVEN:
kx + 2y = 5
3x + y = 1
To find: To determine to value of k for which the system has a unique solution.
We know that the system of equations
a1x + b1y = c1
a2 + b2y = c2
For unique solution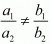
Here,
Hence for 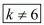 the system of equation has unique solution.
the system of equation has unique solution.
Q.6. Find the value of k for which the following system of equations has a unique solution:
4x +ky + 8 = 0
2x + 2y + 2 = 0
Ans. GIVEN:
4x +ky + 8 = 0
2x + 2y + 2 = 0
To find: To determine to value of k for which the system has a unique solution.
We know that the system of equations
a1x + b1y = c1
a2x + b2y = c2
For unique solution
Here,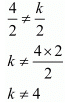
Hence for  the system of equation has unique solution.
the system of equation has unique solution.
Q.7. Find the value of k for which the following system of equations has a unique solution:
4x − 5y = k
2x − 3y = 12
Ans.7. GIVEN:
4x − 5y = k
2x − 3y = 12
To find: To determine to value of k for which the system has a unique solution.
We know that the system of equations
a1x + b1y = c1
a2x + b2y = c2
For unique solution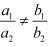
Here,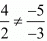
Hence already 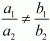 for the system of equation to have unique solution but the value of k should be a real number
for the system of equation to have unique solution but the value of k should be a real number
Hence for k = real number the system of equation has unique solution.
Q.8. Find the value of k for which the following system of equations has a unique solution:
x + 2y = 3
5x + ky + 7 = 0
Ans. GIVEN:
x + 2y = 3
5x + ky + 7 = 0
To find: To determine to value of k for which the system has a unique solution.
We know that the system of equations
a1x + b1y = c1
a2x + b2 y = c2
For unique solution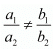
Here,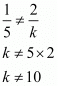
Hence for 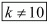 the system of equation has unique solution
the system of equation has unique solution
Q.9. Find the value of k for which each of the following system of equations have infinitely many solutions :
2x + 3y − 5 = 0
6x + ky − 15 = 0
Ans.9. GIVEN:
2x + 3y - 5 = 0
6x + ky - 15 = 0
To find: To determine for what value of k the system of equation has infinitely many solutions
We know that the system of equations
a1x + b1y = c1
a2x + b2 y = c2
Here,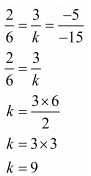
Hence for k = 9 the system of equation have infinitely many solutions
Q.10. Find the value of k for which each of the following system of equations have infinitely many solutions :
4x + 5y = 3
kx + 15y = 9
Ans. GIVEN:
4x + 5y = 3
kx + 15y = 9
To find: To determine for what value of k the system of equation has infinitely many solutions
We know that the system of equations
a1x + b1y = c1
a2x + b2y = c2
For infinitely many solution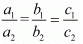
Here,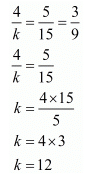
Hence for k = 12 the system of equation have infinitely many solutions.
Q.11. Find the value of k for which each of the following system of equations have infinitely many solutions :
kx − 2y + 6 = 0
4x − 3y + 9 = 0
Ans. GIVEN:
kx − 2y + 6 = 0
4x − 3y + 9 = 0
To find: To determine for what value of k the system of equation has infinitely many solutions
We know that the system of equations
a1x + b1y = c1
a2x + b2y = c2
For infinitely many solution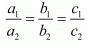
Here,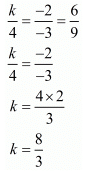
Hence for 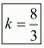 the system of equation have infinitely many solutions.
the system of equation have infinitely many solutions.
Q.12. Find the value of k for which each of the following system of equations have infinitely many solutions :
8x + 5y = 9
kx + 10y = 18
Ans. GIVEN:
8x + 5y = 9
kx + 10y = 18
To find: To determine for what value of k the system of equation has infinitely many solutions
We know that the system of equations
a1x + b1y = c1
a2x + b2y = c2
For infinitely many solution
Here,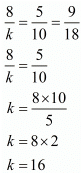
Hence for k = 16 the system of equation have infinitely many solutions
Q.13. Find the value of k for which each of the following system of equations have infinitely many solutions :
2x − 3y = 7
(k + 2) x − (2k + 1)y = 3(2k − 1)
Ans. GIVEN:
2x − 3y = 7
(k + 2) x − (2k + 1)y = 3(2k − 1)
To find: To determine for what value of k the system of equation has infinitely many solutions
We know that the system of equations
a1x + b1y = c1
a2x + b2y = c2
For infinitely many solution
Here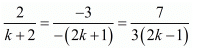
Consider the following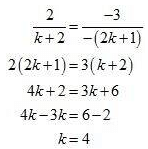
Now consider the following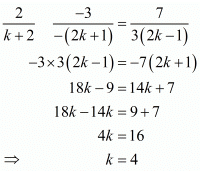
Hence for k = 4 the system of equation have infinitely many solutions.
Q.14. Find the value of k for which each of the following system of equations have infinitely many solutions :
2x + 3y = 2
(k + 2)x + (2k + 1)y = 2(k − 1)
Ans. GIVEN:
2x + 3y = 2
(k + 2)x + (2k + 1)y = 2(k − 1)
To find: To determine for what value of k the system of equation has infinitely many solutions
We know that the system of equations
a1x + b1y = c1
a2x + b2y = c2
For infinitely many solution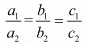
Here,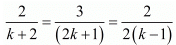
Consider the following for k
Now consider the following
Hence for k = 4 the system of equation have infinitely many solutions.
Q.15. Find the value of k for which each of the following system of equations have infinitely many solutions :
x + (k + 1) y = 4
(k + 1) x + 9 y = 5k + 2
Ans.
GIVEN:
x + (k + 1) y = 4
(k + 1) x + 9 y = 5k + 2
To find: To determine for what value of k the system of equation has infinitely many solutions
We know that the system of equations
a1x + b1y = c1
a2x + b2y = c2
For infinitely many solution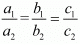
Here,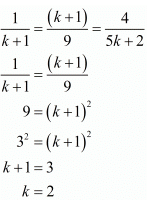
Hence for k = 2 the system of equation have infinitely many solutions.
Q.16. Find the value of k for which each of the following system of equations have infinitely many solutions :
kx + 3y = 2k + 1
2(k + 1)x + 9y = 7k + 1
Ans. GIVEN:
kx + 3y = 2k + 1
2(k + 1)x + 9y = 7k + 1
To find: To determine for what value of k the system of equation has infinitely many solutions
We know that the system of equations
a1x + b1y = c1
a2x + b2y = c2
For infinitely many solution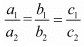
Here,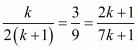
Consider the following relation to find k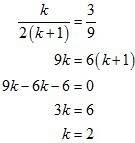
Now consider the following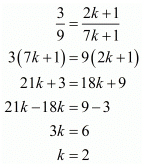
Hence for k = 2 the system of equation have infinitely many solutions
Q.17. Find the value of k for which each of the following system of equations have infinitely many solutions :
2x + (k − 2)y = k
6x + (2k − 1)y = 2k + 5
Ans. GIVEN:
2x + (k − 2)y = k
6x + (2k − 1)y = 2k + 5
To find: To determine for what value of k the system of equation has infinitely many solutions
We know that the system of equations
a1x + b1y = c1
a2x + b2y = c2
For infinitely many solution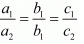
Here,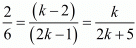
Consider the following relation to find k
Now again consider the following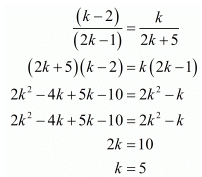
Hence for k = 5 the system of equation have infinitely many solutions
Q.18. Find the value of k for which each of the following system of equations have infinitely many solutions :
2x + 3y = 7
(k + 1)x + (2k − 1)y = 4k + 1
Ans. GIVEN:
2x + 3y = 7
(k + 1)x + (2k − 1)y = 4k + 1
a1x + b1y = c1
a2x + b2y = c2
For infinitely many solution
Here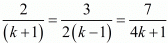
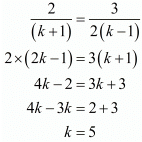
Now again consider the following to find k
Hence for k = 5 the system of equation have infinitely many solutions
Q.19. Find the value of k for which each of the following system of equations have infinitely many solutions :
2x + 3y = k
(k − 1)x + (k + 2)y = 3k
Ans. GIVEN:
2x + 3y = k
(k − 1)x + (k + 2)y = 3k
To find: To determine for what value of k the system of equation has infinitely many solutions
We know that the system of equations
a1x + b1y = c1
a2x + b2y = c2
For infinitely many solution
Here,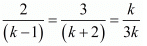
Consider the following to find out k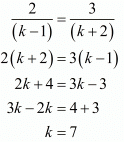
Now again consider the following relation
So the common solution is 7
Hence for k = 7 the system of equation have infinitely many solutions
Q.20. Find the value of k for which each of the following system of equations have no solution :
kx − 5y = 2
6x + 2y = 7
Ans.
kx − 5y = 2
6x + 2y = 7
To find: To determine for what value of k the system of equation has no solution
We know that the system of equations
a1x + b1y = c1
a2x + b2y = c2
For no solution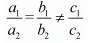
Here,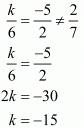
Hence for k = - 15 the system of equation have infinitely many solutions.
Q.21. Find the value of k for which each of the following system of equations have no solution :
x + 2y = 0
2x + ky = 5
Ans.
GIVEN:
x + 2y = 0
2x + ky = 5
To find: To determine for what value of k the system of equation has no solution
We know that the system of equations
a1x + b1y = c1
a2x + b2y = c2
For no solution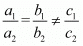
Here,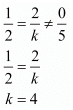
Hence for k = 4 the system of equation has no solution.
FAQs on Chapter 3 - Pair Of Linear Equations In Two Variables, RD Sharma Solutions - (Part-15) - RD Sharma Solutions for Class 10 Mathematics
| 1. How can we determine the solution to a pair of linear equations in two variables? |  |
| 2. Why are pair of linear equations in two variables important in real-life situations? |  |
| 3. What is the significance of finding the solution to a pair of linear equations in two variables? |  |
| 4. How can we check if a given pair of values satisfies a pair of linear equations in two variables? |  |
| 5. Can a pair of linear equations in two variables have more than one solution? |  |

|
Explore Courses for Class 10 exam
|

|
















