Chapter 3 - Pair Of Linear Equations In Two Variables, RD Sharma Solutions - (Part-16) | RD Sharma Solutions for Class 10 Mathematics PDF Download
Page No 3.74
Q.22. Find the value of k for which each of the following system of equations have no solution :
3x − 4y + 7 = 0
kx + 3y − 5 = 0
Ans. GIVEN:
3x − 4y + 7 = 0
kx + 3y − 5 = 0
To find: To determine for what value of k the system of equation has no solution
We know that the system of equations
a1x + b1y = c1
a2x + b2y = c2
For no solution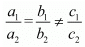
Here,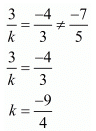
Hence for 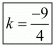 the system of equation has no solution.
the system of equation has no solution.
Q.23. Find the value of k for which each of the following system of equations have no solution :
2x − ky + 3 = 0
3x + 2y − 1 = 0
Ans. GIVEN:
2x − ky + 3 = 0
3x + 2y − 1 = 0
To find: To determine for what value of k the system of equation has no solution
We know that the system of equations
a1x + b1y = c1
a2x + b2y = c2
For no solution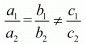
Here,
Hence for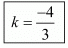 the system of equation has no solution.
the system of equation has no solution.
Q.24. Find the value of k for which each of the following system of equations have no solution :
2x + ky = 11
5x − 7y = 5
Ans. GIVEN:
2x + ky = 11
5x − 7y = 5
To find: To determine for what value of k the system of equation has no solution
We know that the system of equations
a1x + b1y = c1
a2x + b2y = c2
For no solution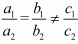
Here,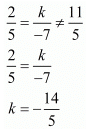
Hence for 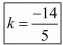 the system of equation has no solution.
the system of equation has no solution.
Q.25. Find the value of k for which each of the following system of equations have no solution :
cx + 2y = 3
12x + cy = 6
Ans. GIVEN:
cx + 2y = 3
12x + cy = 6
To find: To determine for what value of c the system of equation has no solution
We know that the system of equations
a1x + b1y = c1
a2x + b2y = c2
For no solution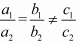
Here,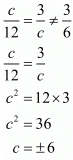
Hence for c = ±6 the system of equation has no solution.
Q.26. For what value of k the following system of equations will be inconsistent?
4x + 6y = 11
2x + ky = 7
Ans. GIVEN:
4x + 6y = 11
2x + ky = 7
To find: To determine for what value of k the system of equation will be inconsistent
We know that the system of equations
a1x + b1y = c1
a2x + b2y = c2
For the system of equation to be inconsistent
Here,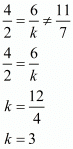
Hence for k = 3 the system of equation will be inconsistent.
Q.27. For what value of α, the system of equations will have no solution?
αx + 3y = α − 3
12x + αy = α
Ans. GIVEN:
αx + 3y = α − 3
12x + αy = α
To find: To determine for what value of k the system of equation has no solution
We know that the system of equations
a1x + b1y = c1
a2x + b2y = c2
For no solution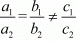
Here,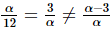
Consider the following for α
Now consider the following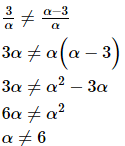
Hence the common value of α is − 6
Hence for α = -6 the system of equation has no solution
Q.28. Find the value of k for which the system has (i) a unique solution, and (ii) no solution.
kx + 2y = 5
3x + y = 1
Ans. GIVEN:
kx + 2y = 5
3x + y = 1
To find: To determine for what value of k the system of equation has
(1) Unique solution
(2) No solution
We know that the system of equations
a1x + b1y = c1
a2x + b2y = c2
(1) For Unique solution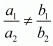
Here,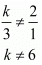
Hence for k ≠ 6 the system of equation has unique solution.
(2) For no solution
Hence for k= 6 the system of equation has no solution
Q.29. (i) Prove that there is a value of c(≠ 0) for which the system
6x + 3y = c − 3
12x + cy = c
has infinitely many solutions. Find this value.
(ii) Find c if the system of equations cx + 3y + 3 – c = 0, 12x + cy – c = 0 has infinitely many solutions?
Ans.
(i) 6x + 3y = c − 3
12x + cy = c
To find: To determine for what value of c the system of equation has infinitely many solution
We know that the system of equations
a1x + b1y = c1
a2x + b2y = c2
For infinitely many solution
Here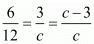
Consider the following
Now consider the following for c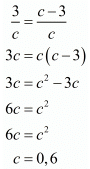
But it is given that c ≠ 0. Hence c = 6
Hence for c = 6 the system of equation have infinitely many solutions.
(ii) If the system of equations a1x+b1y+c1=0 and a2x+b2y+c2=0 has infinitely many solutions, then 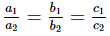
Since, the system of equations cx + 3y + 3 – c = 0, 12x + cy – c = 0 has infinitely many solutions
Therefore,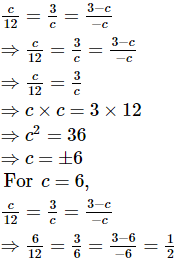
Hence, it holds for c = 6.
For c=−6,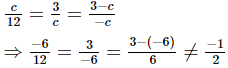
Hence, it does not holds for c=−6.
Hence, the value of c is 6.
Page No 3.74
Q.30. Find the values of k for which the system will have (i) a unique solution, and (ii) no solution. Is there a value of k for which the system has infinitely many solutions?
2x + ky = 1
3x − 5y = 7
Ans. GIVEN:
2x + ky = 1
3x − 5y = 7
To find: To determine for what value of k the system of equation has
(1) Unique solution
(2) No solution
(3) Infinitely many solution
We know that the system of equations
a1x + b1y = c1
a2x + b2y = c2
(1) For Unique solution
Here,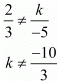
Hence for 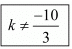 the system of equation has unique solution
the system of equation has unique solution
(2) For no solution
Here,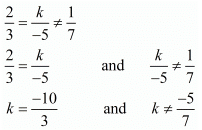
Hence for 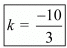 the system of equation has no solution
the system of equation has no solution
(3) For infinitely many solution
Here,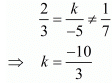
But since here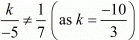
Hence the system does not have infinitely many solutions.
Q.31. For what value of k, the following system of equations will represent the coincident lines?
x + 2y + 7 = 0
2x + ky + 14 = 0
Ans. GIVEN:
x + 2y + 7 = 0
2x + ky + 14 = 0
To find: To determine for what value of k the system of equation will represents coincident lines
We know that the system of equations
a1x + b1y = c1
a2x + b2y = c2
For the system of equation to represent coincident lines we have the following relation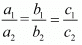
Here,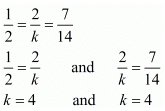
Hence for k = 4 the system of equation represents coincident lines
Q.32. Obtain the condition for the following system of linear equations to have a unique solution
ax + by = c
lx + my = n
Ans. GIVEN:
ax + by = c
lx + my = n
To find: To determine the condition for the system of equation to have a unique equation
We know that the system of equations
a1x + b1y = c1
a2x + b2y = c2
For unique solution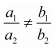
Here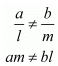
Hence for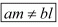 the system of equation have unique solution.
the system of equation have unique solution.
Q.33. Determine the values of a and b so that the following system of linear equations have infinitely many solutions :
(2a − 1) x + 3y − 5 = 0
3x + (b − 1)y − 2 = 0
Ans.
GIVEN:
(2a − 1) x + 3y − 5 = 0
3x + (b − 1)y − 2 = 0
To find: To determine for what value of k the system of equation has infinitely many solutions
We know that the system of equations
a1x + b1y = c1
a2x + b2y = c2
For infinitely many solution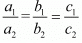
Here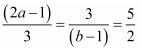
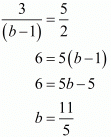
Again consider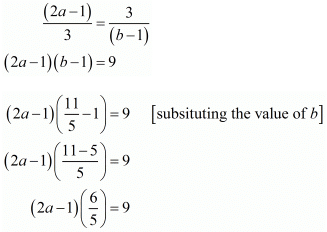
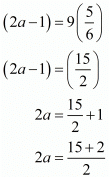
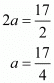
Hence for 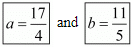 the system of equation has infinitely many solution.
the system of equation has infinitely many solution.
Page No 3.75
Q.34. Find the values of a and b for which the following system of linear equations has infinite number of solutions :
2x − 3y = 7
(a + b) x − (a + b − 3) y = 4a + b
Ans. GIVEN:
2x − 3y = 7
(a + b) x − (a + b − 3) y = 4a + b
To find: To determine for what value of k the system of equation has infinitely many solutions
We know that the system of equations
a1x + b1y = c1
a2x + b2y = c2
For infinitely many solution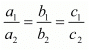
Here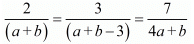
Consider the following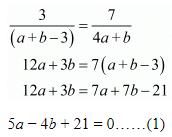
Again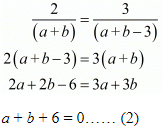
Multiplying eq. (2) by 4 and adding eq. (1)
9a + 45 = 0
a = -5
Putting the value of a in eq. (2)
- 5 + b + 6 = 0
b = -1
Hence for a = -5 and b = -1 the system of equation has infinitely many solution.
Q.35. Find the values of p and q for which the following system of linear equations has infinite number of solutions:
2x + 3y = 9
(p + q) x + (2p − q)y = 3(p + q + 1)
Ans. GIVEN:
2x + 3y = 9
(p + q)x + (2p − q)y = 3(p + q + 1)
To find: To determine for what value of k the system of equation has infinitely many solutions
We know that the system of equations
a1x + b1y = c1
a2x + b2y = c2
For infinitely many solution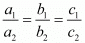
Here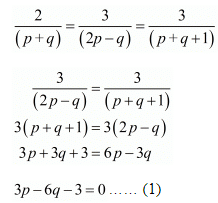
Again consider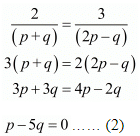
Multiplying eq. (2) by 3 and subtracting from eq. (1)
3p - 6q - 3 - 3p + 15q = 0
9q = 3
q = 1/3
Putting the value of q in eq. (2)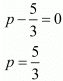
Hence for 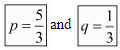 the system of equation has infinitely many solution.
the system of equation has infinitely many solution.
Q.36. Find the values of a and b for which the following system of equations has infinitely many solutions:
(i) (2a − 1)x − 3y = 5
3x + (b − 2) y = 3
(ii) 2x − (2a + 5)y = 5
(2b + 1)x − 9y = 15
(iii) (a − 1)x + 3y = 2
6x + (1 − 2b)y = 6
(iv) 3x + 4y = 12
(a + b)x + 2(a − b)y = 5a − 1
(v) 2x + 3y = 7
(a − b)x + (a + b)y = 3a + b − 2
(vi) 2x + 3y − 7 = 0
(a − 1) x + (a + 1)y = (3a − 1)
(vii) 2x + 3y = 7
(a − 1)x + (a + 2)y = 3a
(viii) x + 2y = 1
(a − b)x + (a + b)y = a + b − 2
(ix) 2x + 3y = 7
2ax + ay = 28 − by
Ans. (i) GIVEN:
(2a − 1)x − 3y = 5
3x + (b − 2) y = 3
To find: To determine for what value of k the system of equation has infinitely many solutions
We know that the system of equations
a1x + b1y = c1
a2x + b2y = c2
For infinitely many solution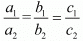
Here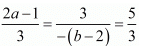
Consider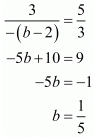
Again consider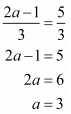
Hence for a = 3 and 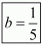 the system of equation has infinitely many solution.
the system of equation has infinitely many solution.
(ii) GIVEN:
2x − (2a + 5)y = 5
(2b + 1)x − 9y = 15
To find: To determine for what value of k the system of equation has infinitely many solutions
We know that the system of equations
a1x + b1y = c1
a2x + b2y = c2
For infinitely many solution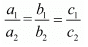
Here
Consider the following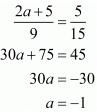
Again consider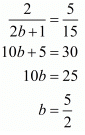
Hence for a = - 1 and 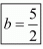 the system of equation has infinitely many solution.
the system of equation has infinitely many solution.
(iii) GIVEN:
(a − 1)x + 3y = 2
6x + (1 − 2b)y = 6
To find: To determine for what value of k the system of equation has infinitely many solutions
We know that the system of equations
a1x + b1y = c1
a2x + b2y = c2
For infinitely many solution
Here
Consider the following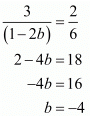
Again consider
Hence for a = 3 and b = -4 the system of equation has infinitely many solution.
(iv) GIVEN:
3x + 4y = 12
(a + b)x + 2(a − b)y = 5a − 1
To find: To determine for what value of k the system of equation has infinitely many solutions
We know that the system of equations
a1x + b1y = c1
a2x + b2y = c2
For infinitely many solution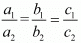
Here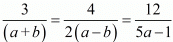
Consider the following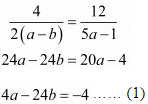
Again consider
Multiplying eq. (2) by 2 and subtracting eq. (1) from eq. 2
2a = 10
a = 5
Substituting the value of ‘a’ in eq. (2) we get
15 - 12b = 3
- 12b = -12
b = 1
Hence for a = 5 and b = 1 the system of equation has infinitely many solution.
(v) GIVEN:
2x + 3y = 7
(a − b)x + (a + b)y = 3a + b − 2
To find: To determine for what value of k the system of equation has infinitely many solutions
We know that the system of equations
a1x + b1y = c1
a2x + b2y = c2
For infinitely many solution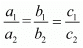
Here
Consider the following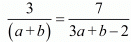
9a + 3b - 6 = 7a + 7b
2a - 4b = 6 ...(1)
Again consider the following
6a + 2b - 4 = 7a - 7b
a - 9b = - 4 ...(2)
Multiplying eq. (2) by 2 and subtracting eq. (1) from eq. (2)
- 14b = - 14
b = 1
Substituting the value of b in eq. (2) we get
a - 9 = - 4
a = 5
Hence for a = 5 and b = 1 the system of equation has infinitely many solution.
(vi) GIVEN:
2x + 3y - 7 = 0
(a - 1) x + (a + 1) y = 3a - 1
To find: To determine for what value of k the system of equation has infinitely many solutions
Rewrite the given equations
2x + 3y - 7 = 0
(a - 1) x + (a + 1) y = 3a - 1
We know that the system of equations
a1x + b1y = c1
a2x + b2y = c2
For infinitely many solution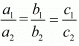
Here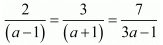
Consider the following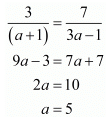
Hence for a = 5 the system of equation have infinitely many solutions.
(vii) GIVEN :
2x + 3y = 7
(a - 1)x + (a + 2) y = 3a
To find: To determine for what value of k the system of equation has infinitely many solutions
We know that the system of equations
a1x + b1y = c1
a2x + b2y = c2
For infinitely many solution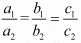
Here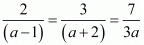
Consider the following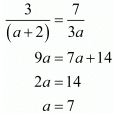
Hence for a = 7 the system of equation have infinitely many solutions.
(viii) Given:
x + 2y = 1
(a − b)x + (a + b) y = a + b − 2
We know that the system of equations
a1x + b1y = c1
a2x + b2y = c2
has infinitely many solutions if
So,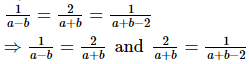
⇒ a + b = 2a − 2b and 2a + 2b − 4 = a + b
⇒ a = 3b and a + b = 4
⇒ a − 3b = 0 and a + b = 4
Solving these two equations, we get
−4b = −4
⇒ b = 1
Putting b = 1 in a + b = 4, we get
a = 3
(ix) Given:
2x + 3y = 7
2ax + ay = 28 − by
⇒ 2ax + (a + b)y = 28
We know that the system of equations
a1x + b1y = c1
a2x + b2y = c2
has infinitely many solutions if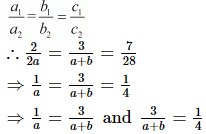
Now,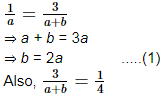
⇒ a + b = 12 .....(2)
Solving (1) and (2), we get
a = 4 and b = 8
FAQs on Chapter 3 - Pair Of Linear Equations In Two Variables, RD Sharma Solutions - (Part-16) - RD Sharma Solutions for Class 10 Mathematics
| 1. What is the graphical method for solving a pair of linear equations in two variables? |  |
| 2. How do you determine if a pair of linear equations in two variables have a unique solution, no solution, or infinitely many solutions? |  |
| 3. How can you verify the solution of a pair of linear equations in two variables algebraically? |  |
| 4. Can a pair of linear equations in two variables be inconsistent? |  |
| 5. How can you determine the solution of a pair of linear equations in two variables if the lines do not intersect on the graph? |  |

|
Explore Courses for Class 10 exam
|

|

















