Chapter 3 - Pair Of Linear Equations In Two Variables, RD Sharma Solutions - (Part-17) | RD Sharma Solutions for Class 10 Mathematics PDF Download

Page No 3.75

Q.37. For which value(s) of λ , do the pair of linear equations    λx + y = λ² and   x + λy = 1   have 
(i) no solution ?
(ii) infinitely many solutions ?
(iii)  a unique solution  ?
Ans. The given linear equations are
λx+y=λ2
x+λy=1
(i) We know that the system of equations
a₁x + b₁y = c₁
a₂x + b₂y = c₂
will have no solution if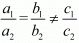

So,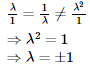

Also,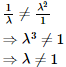

Thus, the given system of equations has no solutions when λ=−1.
(ii) We know that the system of equations
a₁x + b₁y = c₁
a₂x + b₂y = c₂
will have infinitely many solutions if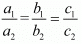


⇒λ² = 1
⇒λ = ±1
Also,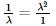

⇒λ3 = 1
⇒ λ = 1
Thus, the given system of equations has infinitely many solutions when λ = 1.
(iii) We know that the system of equations
a₁x + b₁y = c₁
a₂x + b₂ y = c<sub>2
will have a unique solution if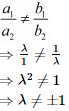

Thus, the given system of equations has a unique solution for all real values of λ except ± 1.</sub>

Page No 3.78

Q.1. 5 pens and 6 pencils together cost Rs 9 and 3 pens and 2 pencils cost Rs 5. Find the cost of 1 pen and 1 pencil.
Ans. Given:
(i) 5 pens and 6 pencils together cost of Rs. 9.
(ii) 3 pens and 2 pencils cost Rs. 5.
To Find: Cost of 1 pen and 1 pencil.
Let
(i) The cost of 1 pen = Rs x.
(ii) The cost of 1 pencil = Rs y.
According to question
 5x + 6y = 9     .....(i)
3x + 2y = 5    .....(ii)
Thus we get the following system of linear equation
 5x + 6y = 9     .....(3) from eq. 1
3x + 2y = 5    .....(4) from eq. 2
By using cross multiplication we have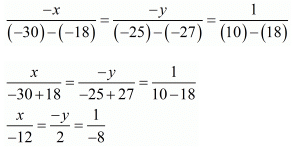

∴




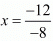
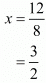
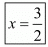
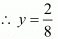
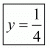
Cost of one pen =
Cost of one pencil =

Q.2. 7 audio cassettes and 3 video cassettes cost Rs 1110, while 5 audio cassettes and 4 video cassettes cost Rs 1350. Find the cost of an audio cassette and a video cassette.
Ans. Given:
(i) 7 Audio cassettes and 3 Video cassettes cost is 1110.
(ii) 5 Audio cassettes and 4 Video cassettes cost Rs. 1350.
To Find: Cost of 1 audio cassette and 1 video cassettes.
Let (i) the cost of 1 audio cassette = Rs. x.
(ii) the cost of 1 video cassette = Rs. y.
According to the given conditions, we have
7x + 3y = 1110    
⇒ 7x + 3y - 1110 = 0          .....(1)
5x + 4y = 1350
⇒ 5x + 4y - 1350 = 0          .....(2)
Thus, we get the following system of linear equation,
7x + 3y - 1110 = 0          .....(1)
⇒ 5x + 4y - 1350 = 0          .....(2)
By using cross multiplication, we have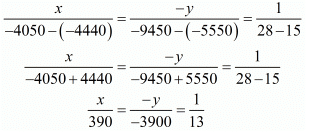


Hence cost of 1 audio cassette = Rs. 30
Hence cost of 1 video cassette = Rs.300

Page No 3.78

Q.3. Reena has pend and pencils which together are 40 in number. If she has 5 more pencils and 5 less pens, the number of pencils would become 4 times the number of pens. Find the original number of pens and pencils.
Ans. Given:
(i) Total numbers of pens and pencils = 40.
(ii) If she has 5 more pencil and 5 less pens, the number of pencils would be 4 times the number of pen.
To find: Original number of pens and pencils.
Suppose original number of pencil = x
And original number of pen = y
According the given conditions, we have,
x + y = 40,
x + y - 40 = 0     ....(1)
5 + x = 4(y - 5)
5 + x = 4y - 20
x - 4y + 5 + 20 = 0
x - 4y + 25 = 0     ....(2)
Thus we got the following system of linear equations
x + y - 40  = 0     ....(1)
x - 4y + 25 = 0     ....(2)
Substituting the value of y from equation 1 in equation 2 we get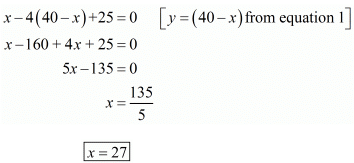

Substituting the value of y in equation 1 we get
27 + y = 40,
y = 40 - 27
y = 13
Hence we got the result number of pencils is x = 27 and number of pens are y = 13.

Q.4. 4 tables and 3 chairs, together, cost Rs 2,250 and 3 tables and 4 chairs cost Rs 1950. Find the cost of 2 chairs and 1 table.
Ans. Given:
(i) Cost of 4 tables and 3 chairs = Rs 2250.
(ii) Cost of 3 tables and 4 chairs = Rs 1950.
To find: The cost of 2 chairs and 1 table.
Suppose, the cost of 1 table = Rs x.
The cost of 1 chair = Rs y.
According to the given conditions,
4x + 3y = 2250,
4x + 3y − 2200 = 0 …… (1)
3x + 4y = 1950,
3x + 4y − 1950 = 0 …… (2)
Solving eq. (1) and Eq. (2) by cross multiplication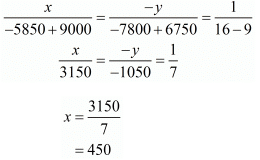

∴ cost of table =Rs. 450
cost of 1 table = Rs. 450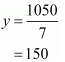

∴ cost of 1 chairs = Rs. 150.
cost of 2 chairs = Rs. 300
Hence total cost of 2 chairs and 1 table = Rs. 750

Q.5. 3 bags and 4 pens together cost Rs 257 whereas 4 bags and 3 pens together cost Rs 324. Find the total cost of 1 bag and 10 pens.
Ans. Given:
(i) Cost of 3 bags and 4 pens = Rs. 257.
(ii) Cost of 4 bags and 3 pens = Rs. 324.
To Find: Cost of 1 bag and 10 pens.
Suppose, the cost of 1 bag = Rs. x.
and the cost 1 pen = Rs. y.
According to the given conditions, we have
3x + 4y = 257,
3x + 4y − 257 = 0 …… (1)
4x + 3y = 324
4x +3y − 324 = 0 …… (2)
Solving equation 1 and 2 by cross multiplication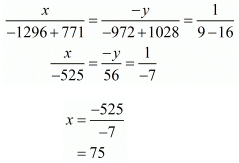

∴ cost of 1 bag = Rs. 75.
cost of 1 bag = Rs. 75.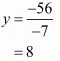

∴ Cost of 1 pen = Rs.8.
Cost of 10 pen = Rs.80.
Total cost of 1 bag and 10 pens = Rs. 155
Hence total cost of 1 bag and 10 pens = Rs. 155

Page No 3.79.

Q.6. 5 books and 7 pens together cost Rs 79 whereas 7 books and 5 pens together cost Rs 77. Find the total cost of 1 book and 2 pens.
Ans. Given:
(i) Cost of 5 books and 7 pens = Rs. 79.
(ii) Cost of 7 books and 5 pens = Rs. 77.
To find: Cost of 1 book and 2 pens.
Suppose the cost of 1 book = Rs x.
and the cost of 1 pen = Rs y.
According to the given conditions, we have
5x + 7y = 79
5x + 7y − 79 = 0 …… (1)
7x + 5y = 77,
5x + 7y − 77 = 0 …… (2)
Thus we get the following system of linear equation,
5x + 7y - 79 = 0 and
5x + 7y - 77 = 0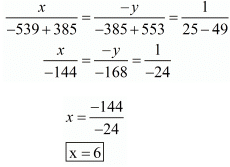


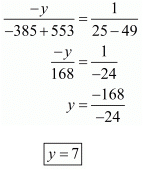
Hence, the cost of 1 book = Rs 6
and the cost of 1 pen = Rs 7.
Therefore the cost of 2 pen = Rs 14.
Total cost of 1 book and 2 pens = 14 + 6 = 20
Total cost of 1 book and 2 pens = Rs. 20
Hence total cost of 1 book and 2 pens = Rs. 20

Q.7. Jamila sold a table and a chair for Rs. 1050 , thereby making a profit of 10% on the table and 25% on the chair. If she  had taken a profit of 25% on the table and 10% on the chair she would have got   Rs. 1065. Find the cost price of each .
Ans. Let the CP of the table be Rs x and that of the chair be Rs y.
Case I: Profit on table =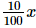 
We know SP − CP = Profit
⇒ SP = Profit + CP
⇒ SP =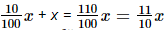
Profit on chair =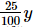
SP =
Total SP =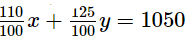
110x + 125y = 105000      .....(i)
Case II: Profit on table =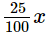
⇒ SP = Profit + CP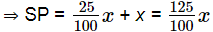

Profit on chair =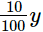
SP =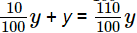
Total SP =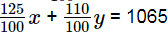
125x + 110y = 106500   .....(ii)
From (i) and (ii), we have
235(x + y) = 211500
⇒ x + y = 900      .....(iii)
Subtracting (i) from (ii), we have
15(x − y) = 1500
⇒ x − y = 100                                    .....(iv)
Solving (iii) and (iv), we get
x = 500 and y = 400
Thus, CP of table = Rs 500 and CP of chair = Rs 400.

Q.8. Susan invested certain amount of money in two schemes A and B , which offer interest at the rate of 8% per annum and 9% per annum , respectively . She received Rs.1860 as annual interest .However, had she interchanged the amount of investment in the two schemes , she would have received  Rs. 20 more as annual interest . How much money did she invest in each scheme ?
Ans. Let the money invested in Scheme A be Rs x and that in Scheme B be Rs y.

So, Interest in scheme A =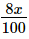
Interest in scheme B =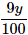
Total annual interest =
⇒ 8x + 9y = 186000         .....(i)
After interchaning the amounts in the two schemes, the new total annual interest =
Now,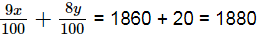

⇒ 9x + 8y = 188000             .....(ii)
Adding (i) and (ii), we get
17x + 17y = 374000
⇒ x + y = 22000                  .....(iii)
Subtracting (i) from (ii), we get
x − y = 2000                       .....(iv)
Adding (iii) and (iv), we get
2x = 24000
⇒ x = 12000
Puting x = 12000 in (iii), we get
12000 + y = 22000
⇒ y = 10000
So, the money invested in scheme A = Rs 12,000 and in scheme B = Rs 10,000.

Q.9. The coach of a cricket team buys 7 bats and 6 balls for Rs 3800. Later, he buys 3 bats and 5 balls for Rs 1750. Find the cost of each bat and each ball.
Ans. Given: (i) 7 bats and 6balls cost is Rs3800
(ii) 3 bats and 5balls cost is Rs1750
To find: Cost of 1 bat and 1 ball
Let (i) the cost of 1 bat = Rs. x.
(ii) the cost of 1 ball = Rs. y.
According to the given conditions, we have
7x + 6y = 3800
7x + 6y - 3800 = 0   ....(1)
3x + 5y = 1750
3x + 5y - 1750 = 0   ....(2)
Thus, we get the following system of linear equation,
7x + 6y − 3800 = 0 …… (1)
3x + 5y − 1750 = 0 …… (2)
By using cross multiplication, we have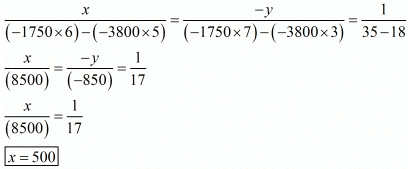


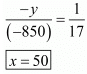
Hence cost of 1 bat = x = 500
Hence cost of 1 ball = x = 50

Q.10. A lending library has a fixed charge for the first three days and additional charge for each day thereafter. Saritha paid Rs 27 for a book kept for seven days, while Susy paid Rs 21 for the book she kept for five days. Find the fixed charge and the charge for each extra day.
Ans.10.
To find:
(1) the fixed charge
(2) The charge for each day
Let the fixed charge be Rs x
And the extra charge per day be Rs y.
According to the given conditions,
x + 4y = 27
x + 4y - 27 = 0   ....(1)
x + 2y = 21
x + 2y - 21 = 0   ....(2)
Subtracting equation 1 and 2 we get
2y = 6
y = 3
Substituting the value of y in equation 1 we get
x + 4(3) - 27 = 0
x + 12 - 27 = 0
x = 15
Hence the fixed charge is x Rs 15 and the charge of each day y = Rs 3

Q.11. The cost of 4 pens and 4 pencil boxes is  Rs.100 . Three times the cost of a pen is  Rs.15 more than the cost of a pencil box . Form the pair of linear equations for the above situation . Find the cost of a pen and a pencil box.
Ans.11. Let the cost of 1 pen be Rs. x and that of 1 pencil box be Rs. y.
Now,
Cost of 4 pens + Cost of 4 pencil boxes = Rs.100
(Given)
⇒ 4x + 4y = 100
⇒ x + y = 25            .....(i)
Also,
3 × Cost of  a pen = Cost of a pencil box + Rs. 15
3x = y + 15
⇒ 3x − y = 15               .....(ii)
Adding (i) and (ii), we get
4x = 40
⇒ x = 10
Putting x = 10 in (i), we get
10 + y = 25
⇒ y = 15
Thus, the cost of a pen = Rs. 10 and that of a pencil box = Rs. 15.