Chapter 3 - Pair Of Linear Equations In Two Variables, RD Sharma Solutions - (Part-20) | RD Sharma Solutions for Class 10 Mathematics PDF Download
Page No 3.86
Q.14. The sum of the digits of a two-digit number is 9. Also, nine times this number is twice the number obtained by reversing the order of the digits. Find the number.
Ans. Let the digits at units and tens place of the given number be x and y respectively. Thus, the number is 10y + x.
The sum of the two digits of the number is 9. Thus, we have x + y = 9
After interchanging the digits, the number becomes 10x + y.
Also, 9 times the number is equal to twice the number obtained by reversing the order of the digits. Thus, we have
9(10y + x) = 2(10x + y)
⇒ 90y + 9x = 20x + 2y
⇒ 20x 2y - 90y - 9x = 0
⇒ 11x - 88y = 0
⇒ 11 (x - 8y) = 0
⇒ x - 8y = 0
So, we have the systems of equations
x + y = 9
x - 8y = 0
Here x and y are unknowns. We have to solve the above systems of equations for x and y.
Substituting x = 8y from the second equation to the first equation, we get
8y + y = 9
⇒ 9y = 9
⇒ 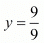
⇒ y = 1
Substituting the value of y in the second equation, we have
x - 8 x 1 = 0
⇒ x - 8 = 0
⇒ x = 8
Hence, the number is 10 x 1 + 8 = 18
Q.15. Seven times a two-digit number is equal to four times the number obtained by reversing the digits. If the difference between the digits is 3. Find the number.
Ans. Let the digits at units and tens place of the given number be x and y respectively. Thus, the number is 10 y + x.
The difference between the two digits of the number is 3. Thus, we have x - y = ±3
After interchanging the digits, the number becomes 10x + y.
Seven times the number is equal to four times the number obtained by reversing the order of the digits. Thus, we have
7(10y + x) = 4(10x + y)
⇒ 70y + 7x = 40x + 4y
⇒ 40x + 4y - 70y - 7x = 0
⇒ 33x - 66y = 0
⇒ 33(x - 2y) = 0
⇒ x - 2y = 0
So, we have two systems of simultaneous equations
x - y = 3,
x - 2y = 0
x - y = -3
x - 2y = 0
Here x and y are unknowns. We have to solve the above systems of equations for x and y.
(i) First, we solve the system
x - y = 3,
x - 2y = 0
Multiplying the first equation by 2 and then subtracting from the second equation, we have
(x - 2y) - 2(x - y) = 0 - 2 x 3
⇒ x - 2y - 2x + 2y = - 6
⇒ - x = - 6
⇒ x = 6
Substituting the value of x in the first equation, we have
6 - y = 3
⇒ y = 6 - 3
⇒ y = 3
Hence, the number is 10 x 3 + 6 = 36
(ii) Now, we solve the system
x - y = - 3
x - 2y = 0
Multiplying the first equation by 2 and then subtracting from the second equation, we have
(x - 2y) - 2(x - y) = 0 - (-3 x 2)
⇒ x - 2y - 2x + 2y = 6
⇒ - x = 6
⇒ x = -6
Substituting the value of x in the first equation, we have
- 6 - y = - 3
⇒ y = - 6 + 3
⇒ y = - 3
But, the digits of the number can’t be negative. Hence, the second case must be removed.
Q.16. Two numbers are in the ratio 5 : 6 . If 8 is subtracted from each of the numbers , the ratio becomes 4 : 5 . Find the numbers .
Ans. Let the two numbers be x and y.
So,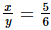
⇒6x = 5y
⇒6x − 5y = 0 .....(i)
Now, when 8 is subtracted from each of the numbers, then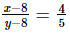
⇒5x − 40 = 4y − 32
⇒5x − 4y = 8 .....(ii)
Multiplying (i) with 4 and (ii) with 5, we get
24x − 20y = 0 .....(iii)
25x − 20y = 40 .....(iv)
Subtracting (iii) from (iv), we get
x = 40
Putting x = 40 in (i), we get
240 − 5y = 0
⇒ y = 48
Thus, the two numbers are 40 and 48.
Q.17. A two-digit number is obtained by either multiplying the sum of the digits by 8 and then subtracting 5 or by multiplying the difference of the digits by 16 and then adding 3 . Find the number .
Ans. Let the digits of the two digit number be x and y. So, the two digit number will be 10x + y.
Now, according to the given condition the number is obtained in two ways.
Case I: 8(x + y) − 5 = 10x + y
⇒ 8x + 8y − 5 = 10x + y
⇒ 2x −7y = −5 .....(1)
Case II: 16(x − y) + 3 = 10x + y
⇒ 16x − 16y + 3 = 10x + y
⇒ 6x − 17y = −3 .....(2)
Multiplying (1) by 3, we get
6x − 21y = −15 .....(3)
Subtracting (2) from (3), we get
− 4y = −12
⇒ y = 3
Putting y = 3 in (1), we get
2x − 21 = −5
⇒ 2x = 16
⇒ x = 8
So, the required number is 10x + y = 10 × 8 + 3 = 83.
Page No 3.88
Q.1. The numerator of a fraction is 4 less than the denominator. If the numerator is decreased by 2 and denominator is increased by 1, then the denominator is eight times the numerator. Find the fraction.
Ans. Let the numerator and denominator of the fraction be x and y respectively. Then the fraction is x/y
The numerator of the fraction is 4 less the denominator. Thus, we have
x = y - 4
⇒ x - y = - 4
If the numerator is decreased by 2 and denominator is increased by 1, then the denominator is 8 times the numerator. Thus, we have
y + 1 = 8(x - 2)
⇒ y + 1 = 8x -16
⇒ 8x - y = 1 + 16
⇒ 8x - y = 17
So, we have two equations
x - y = - 4
8x - y = 17
Here x and y are unknowns. We have to solve the above equations for x and y.
Subtracting the second equation from the first equation, we get
(x - y) - (8x - y) = -4 -17
⇒ x - y - 8x + y = -21
⇒ - 7x = -21
⇒ 7x = 21
⇒ 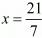
⇒ x = 3
Substituting the value of x in the first equation, we have
3 - y = - 4
⇒ y = 3 + 4
⇒ y = 7
Hence, the fraction is 3/7
Page No 3.89
Q.2. A fraction becomes 9/11 if 2 is added to both numerator and the denominator. If 3 is added to both the numerator and the denominator it becomes 5/6. Find the fraction.
Ans. Let the numerator and denominator of the fraction be x and y respectively. Then the fraction is x/y
If 2 is added to both numerator and the denominator, the fraction becomes 9/11 Thus, we have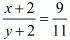
⇒ 11(x + 2) = 9(y + 2)
⇒ 11 x + 22 = 9y + 18
⇒ 11x - 9y = 18 - 22
⇒ 11 x - 9y + 4 = 0
If 3 is added to both numerator and the denominator, the fraction becomes 5/6.Thus, we have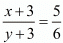
⇒ 6(x + 3) = 5(y + 3)
⇒ 6x + 18 = 5y + 15
⇒ 6x - 5y = 15 - 18
⇒ 6x - 5y + 3 = 0
So, we have two equations
11x - 9y + 4 = 0
6x - 5y + 3 = 0
Here x and y are unknowns. We have to solve the above equations for x and y.
By using cross-multiplication, we have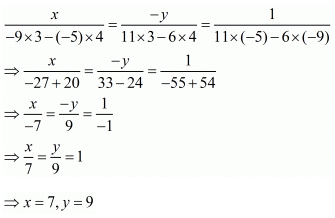
Hence, the fraction is 7/9.
Q.3. A fraction becomes 1/3 if 1 is subtracted from both its numerator and denominator. It 1 is added to both the numerator and denominator, it becomes 1/2. Find the fraction.
Ans. Let the numerator and denominator of the fraction be x and y respectively. Then the fraction is x/y
If 1 is subtracted from both numerator and the denominator, the fraction becomes 1/3. Thus, we have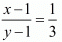
⇒ 3(x - 1) = y - 1
⇒ 3x - 3 = y - 1
⇒ 3x - y - 2 = 0
If 1 is added to both numerator and the denominator, the fraction becomes 1/2 Thus, we have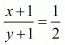
⇒ 2(x + 1) = y + 1
⇒ 2x + 2 = y + 1
⇒ 2x - y + 1 = 0
So, we have two equations
3x - y - 2 = 0
2x - y + 1 = 0
Here x and y are unknowns. We have to solve the above equations for x and y.
By using cross-multiplication, we have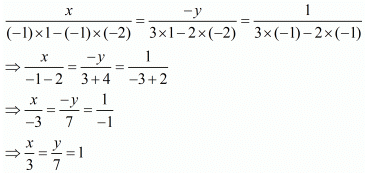
⇒ x = 3, y = 7
Hence, the fraction is 3/7.
Q.4. If we add 1 to the numerator and subtract 1 from the denominator, a fraction becomes 1. It also becomes 1/2 if we only add 1 to the denominator. What is the fraction?
Ans. Let the numerator and denominator of the fraction be x and y respectively. Then the fraction is x/y
If 1 is added to the numerator and 1 is subtracted from the denominator, the fraction becomes 1. Thus, we have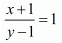
⇒ x + 1 = y - 1
⇒ x + 1 - y + 1 = 0
⇒ x - y + 2 = 0
If 1 is added to the denominator, the fraction becomes 1/2 Thus, we have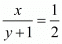
⇒ 2x = y + 1
⇒ 2x - y - 1 = 0
So, we have two equations
x - y + 2 = 0
2x - y - 1 = 0
Here x and y are unknowns. We have to solve the above equations for x and y.
By using cross-multiplication, we have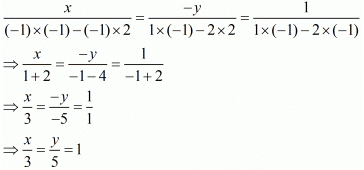
⇒ x = 3, y = 5
Hence, the fraction is 3/5.
Q.5. If the numerator of a fraction is multiplied by 2 and the denominator is reduced by 5 the fraction becomes 6/5. And, if the denominator is doubled and the numerator is increased by 8, the fraction becomes 2/5. find the fraction.
Ans. Let the numerator and denominator of the fraction be x and y respectively. Then the fraction is x/y
If the numerator is multiplied by 2 and the denominator is reduced by 5, the fraction becomes 6/5. Thus, we have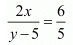
⇒ 10x = 6(y - 5)
⇒ 10x = 6y - 30
⇒ 10x - 6y + 30 = 0
⇒ 2(5x - 3y + 15) = 0
⇒ 5x - 3y + 15 = 0
If the denominator is doubled and the numerator is increased by 8, the fraction becomes 2/5. Thus, we have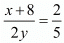
⇒ 5(x + 8) = 4y
⇒ 5x + 40 = 4y
⇒ 5x - 4y + 40 = 0
So, we have two equations
5x - 3y + 15 = 0
5x - 4y + 40 = 0
Here x and y are unknowns. We have to solve the above equations for x and y.
By using cross-multiplication, we have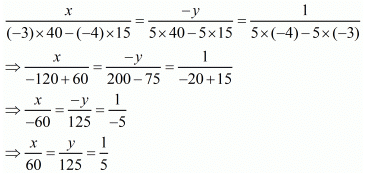
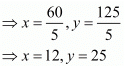
Hence, the fraction is 12/25
Q.6. When 3 is added to the denominator and 2 is subtracted from the numerator a fraction becomes 1/4. And when 6 is added to numerator and the denominator is multiplied by 3, it becomes 2/3. Find the fraction.
Ans. Let the numerator and denominator of the fraction be x and y respectively. Then the fraction is x/y
If 3 is added to the denominator and 2 is subtracted from the numerator, the fraction becomes 1/4. Thus, we have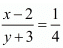
⇒ 4(x - 2) = y + 3
⇒ 4x - 8 = y + 3
⇒ 4x - y - 11 = 0
If 6 is added to the numerator and the denominator is multiplied by 3, the fraction becomes 2/3. Thus, we have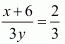
⇒ 3(x + 6) = 6y
⇒ 3x + 18 = 6y
⇒ 3x - 6y + 18 = 0
⇒ 3(x - 2y + 6) = 0
⇒ x - 2y + 6 = 0
So, we have two equations
4x - y - 11 = 0
x - 2y + 6 = 0
Here x and y are unknowns. We have to solve the above equations for x and y.
By using cross-multiplication, we have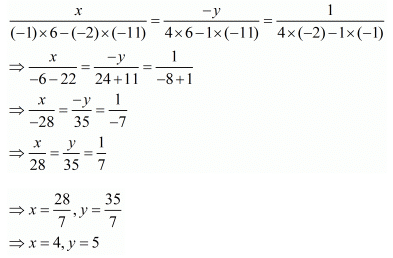
Hence, the fraction is 4/5.
FAQs on Chapter 3 - Pair Of Linear Equations In Two Variables, RD Sharma Solutions - (Part-20) - RD Sharma Solutions for Class 10 Mathematics
| 1. How can we solve a pair of linear equations in two variables using the elimination method? |  |
| 2. What is the significance of the graphical method in solving a pair of linear equations in two variables? |  |
| 3. Can a pair of linear equations in two variables have more than one solution? |  |
| 4. How can we determine if a pair of linear equations in two variables is consistent or inconsistent? |  |
| 5. What is the difference between the substitution method and the elimination method for solving a pair of linear equations in two variables? |  |

|
Explore Courses for Class 10 exam
|

|
















