Chapter 3 - Pair Of Linear Equations In Two Variables, RD Sharma Solutions - (Part-22) | RD Sharma Solutions for Class 10 Mathematics PDF Download

Page No 3.92

Q.8. Father's age is three times the sum of age of his two children. After 5 years his age will be twice the sum of ages of two children. Find the age of father.
Ans. Let the present age of father be x years and the present ages of his two children’s be y and z years.
The present age of father is three times the sum of the ages of the two children’s. Thus, we have
x = 3(y + z)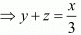

After 5 years, father’s age will be (x + 5) years and the children’s age will be (y + 5) and (z + 5) years. Thus using the given information, we have
x + 5 = 2(y + 5) + (z + 5)
⇒ x + 5 = 2(y + 5 + z + 5)
⇒ x = 2(y + z) + 20 - 5
⇒ x = 2(y + z) + 15
So, we have two equations

x = 2(y + z) + 15
Here x, y and z are unknowns. We have to find the value of x.
Substituting the value of (y + z) from the first equation in the second equation, we have
By using cross-multiplication, we have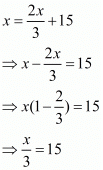

⇒ x = 15 x 3
⇒ x = 45
Hence, the present age of father is 45 years.

Q.9. Two years ago, a father was five times as old as his son. Two year later, his age will be 8 more than three times the age of the son. Find the present ages of father and son.
Ans. Let the present age of father be x years and the present age of his son be y years.
After 2 years, father’s age will be (x + 2) years and the age of son will be (x + 2) years. Thus using the given information, we have
x + 2 = 3(y + 2) + 8
⇒ x + 2 = 3y + 6 + 8
⇒ x - 3y - 12 = 0
Before 2 years, the age of father was (x - 2) years and the age of son was (y - 2) years. Thus using the given information, we have
x - 2 = 5(y - 2)
⇒ x - 2 = 5y - 10
⇒ x - 5y + 8 = 0
So, we have two equations
x - 3y - 12 = 0
x - 5y + 8 = 0
Here x and y are unknowns. We have to solve the above equations for x and y.
By using cross-multiplication, we have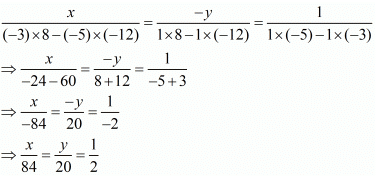


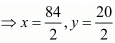
⇒ x = 42, y = 10
Hence, the present age of father is 42 years and the present age of son is 10 years.

Q.10. A is elder to B by 2 years. A's father F is twice as old as A and B is twice as old as his sister S. If the ages of the father and sister differ by 40 years, find the age of A.
Ans. Let the present ages of A, B, F and S be x, y, z and t years respectively.
A is elder to B by 2 years. Thus, we have x = y + 2
F is twice as old as A. Thus, we have z = 2x
B is twice as old as S. Thus, we have y = 2t
The ages of F and S is differing by 40 years. Thus, we have z - t = 40
So, we have four equations
x = y + 2,    ......(1)
z = 2x,    ......(2)
y = 2t,    ......(3)
z - t = 40    ......(4)
Here x, y, z and t are unknowns. We have to find the value of x.
By using the third equation, the first equation becomes x = 2t + 2
From the fourth equation, we have t = z - 40
Hence, we have
x = 2(z - 40) + 2
= 2z - 80 + 2
= 2z - 78
Using the second equation, we have
x = 2 x 2x - 78
⇒ x = 4x - 78
⇒ 4x - x = 78
⇒ 3x = 78
⇒
⇒ x = 26
Hence, the age of A is 26 years.

Page No 3.92

Q.11. The ages of two friends Ani and Biju differ by 3 years. Ani's father Dharma is twice as old as Ani and Biju as twice as old as his sister Cathy. The ages of Cathy and Dharam differ by 30 years. Find the ages of Ani and Biju.
Ans.11. Let the present ages of Ani, Biju, Dharam and Cathy be x, y, z and t years respectively.
The ages of Ani and Biju differ by 3 years. Thus, we have
x - y = ±3
⇒ x = y ±3
Dharam is twice as old as Ani. Thus, we have z = 2x
Biju is twice as old as Cathy. Thus, we have y = 2t
The ages of Cathy and Dharam differ by 30 years. Clearly, Dharam is older than Cathy. Thus, we have z - t = 30
So, we have two systems of simultaneous equations
(i) x = y + 3,
z = 2x,
y = 2t,
z - t = 30
(ii) x = y - 3
z = 2x,
y = 2t,
z - t = 30
Here x, y, z and t are unknowns. We have to find the value of x and y.
(i) By using the third equation, the first equation becomes x = 2t + 3
From the fourth equation, we have
t = z - 30
Hence, we have
x = 2(z - 30) + 3
= 2z - 60 + 3
= 2z - 57
Using the second equation, we have
x = 2 x 2x - 57
⇒ x = 4x - 57
⇒ 4x - x = 57
⇒ 3x = 57

From the first equation, we have
x = y + 3
⇒ y = x - 3
⇒ y = 19 - 3
⇒ y = 16
Hence, the age of Ani is 19 years and the age of Biju is 16 years.
(ii) By using the third equation, the first equation becomes x = 2t - 3
From the fourth equation, we have
t = z - 30
Hence, we have
x = 2(z - 30) - 3
= 2z - 60 - 3
= 2z - 63
Using the second equation, we have
x = 2 x 2x - 63
⇒ x = 4x - 63
⇒ 4x - x = 63
⇒ 3x = 63
⇒
⇒ x = 21
From the first equation, we have
x = y - 3
⇒ y = x + 3
⇒ y = 21 + 3
⇒ y = 24
Hence, the age of Ani is 21 years and the age of Biju is 24 years.
Note that there are two possibilities.

Q.12. Two years ago, Salim was thrice as old as his daughter and six years later , he will be four years older than twice her age . How old are they now ?
Ans. Let the present ages of Salim be x years and that of her daughter be y years.
Two years ago, the age of Salim was (x − 2) years and that of her daughter was (y − 2).
It is given that Salim was thrice as old as her daughter two years ago. So,
x − 2 = 3(y − 2)
⇒ x − 2 = 3y − 6
⇒ x − 3y = −4      .....(i)
Six years later, the age of Salim will be (x + 6) and that of her daughter will be (y + 6).
∴ x + 6 = 2(y + 6) + 4
⇒ x − 2y = 10         .....(ii)
Subtracting (ii) from (i), we get
−y = −14
⇒ y = 14
Putting y = 14 in (ii), we get
x − 28 = 10
⇒ x = 38
Hence, the present age of Salim is 38 years and that of her daughter is 14 years.

Q.13. The age of the father is twice the sum of the ages of his two children . After 20 years , his age will be eual to the sum of the ages of his children . Find the age of the father.
Ans. Let the present age of the father be x years and the sum of the present ages of his two children be y years.
Now according to the given conditions,
Case I: x = 2y
⇒ x − 2y = 0           .....(i)
Case II: After 20 years, the age of the father will be (x + 20) years and the sum of the ages of the two children will be y + 20 + 20 = (y + 40) years.
So, x + 20 = y + 40
⇒ x − y = 20           .....(ii)
Subtracting (ii) from (i), we get
− y = −20
⇒ y = 20
Putting y = 20 in (i), we get
x − 40 = 0
⇒ x = 40
Hence, the present age of the father is 40 years.