Chapter 7 - Coordinate Geometry, RD Sharma Solutions - (Part-3) | RD Sharma Solutions for Class 10 Mathematics PDF Download

Page No 6.16

Ques.31. Find the value of x such that PQ = QR where the coordinates of P, Q and R are (6,−1), (1, 3) and (x, 8) respectively.
Ans. The distance d between two points (x₁,y₁) and (x₂,y₂) is given by the formula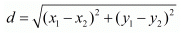

The three given points are P(6,−1), Q(1,3) and R(x,8).
Now let us find the distance between ‘P’ and ‘Q’.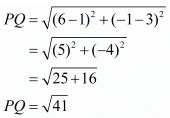

Now, let us find the distance between ‘Q’ and ‘R’.

It is given that both these distances are equal. So, let us equate both the above equations,
PQ = QR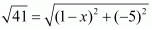

Squaring on both sides of the equation we get,
41 = (1-x)² + (-5)²
41 = 1+x²-2x+25
15 = x² - 2x
Now we have a quadratic equation. Solving for the roots of the equation we have,
x² - 2x - 15 = 0
x² - 5x + 3x - 15 = 0
x(x-5) + 3(x-5) = 0
(x-5)(x+3) = 0
Thus the roots of the above equation are 5 and −3.
Hence the values of ‘x’ are 5 or -3.

Page No 6.16

Ques.32. Prove that the points (0, 0), (5, 5) and (−5, 5) are the vertices of a right isosceles triangle.
Ans. The distance d between two points (x₁,y₁) and (x₂,y₂) is given by the formula

In an isosceles triangle there are two sides which are equal in length.
By Pythagoras Theorem in a right-angled triangle the square of the longest side will be equal to the sum of squares of the other two sides.
Here the three points are A(0,0), B(5,5) and C(−5,5).
Let us check the length of the three sides of the triangle.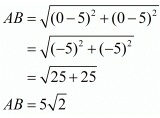



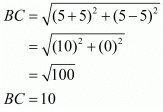
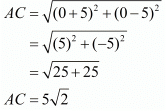
Here, we see that two sides of the triangle are equal. So the triangle formed should be an isosceles triangle.
Further it is seen that BC² = AB² + AC²
If in a triangle the square of the longest side is equal to the sum of squares of the other two sides then the triangle has to be a right-angled triangle.
Hence proved that the triangle formed by the three given points is an right-angled isosceles triangle.

Page No 6.16:

Ques.33. If the point P(x, y) is equidistant from the points A(5, 1) and B (1, 5), prove that x = y.
Ans. The distance d between two points (x₁,y₁) and (x₂,y₂) is given by the formula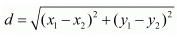

The three given points are P(x, y), A(5,1) and B(1,5).
Now let us find the distance between ‘P’ and ‘A’.

Now, let us find the distance between ‘P’ and ‘B’.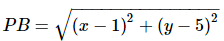

It is given that both these distances are equal. So, let us equate both the above equations,
PA = PB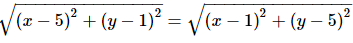

Squaring on both sides of the equation we get,
(x−5)² + (y−1)²
= (x−1)²+(y−5)²
⇒x²+25−10x+y²+1−2y=x²+1−2x+y²+25−10y
⇒26−10x−2y=26−10y−2x
⇒10y−2y=10x−2x
⇒8y=8x
⇒y=x
Hence we have proved that x = y.

Page No 6.16

Ques.34. If Q (0,1) is equidistant from P (5, −3) and R (x, 6), find the values of x. Also, find the distances QR and PR.
Ans. The distance d between two points (x₁,y₁) and (x₂,y₂) is given by the formula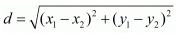

The three given points are Q(0,1), P(5,−3) and R(x,6).
Now let us find the distance between ‘P’ and ‘Q’.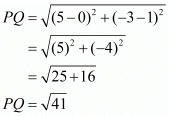

Now, let us find the distance between ‘Q’ and ‘R’.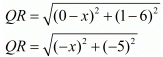

It is given that both these distances are equal. So, let us equate both the above equations,
PQ = QR

Squaring on both sides of the equation we get,
41 = (-x)² + (-5)²
41 = x² + 25
x² = 16
x = ±4
Hence the values of ‘x’ are 4 or -4.
Now, the required individual distances,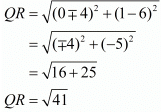

Hence the length of ‘QR’ is √41 units.
For ‘PR’ there are two cases. First when the value of ‘x’ is 4,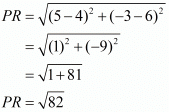

Then when the value of ‘x’ is −4,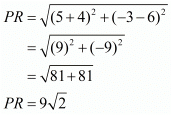

Hence the length of ‘PR’ can beunits

Page No 6.16

Ques.35. Find the values of y for which the distance between the points P (2,−3) and Q(10,y) is 10 units.
Ans.The distance d between two points (x₁,y₁) and (x₂,y₂) is given by the formula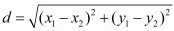

The distance between two points P(2,−3) and Q(10,y) is given as 10 units. Substituting these values in the formula for distance between two points we have,

Now, squaring the above equation on both sides of the equals sign
100 = (-8)² + (-3-y)²
100 = 64 + 9 + y² + 6y
27 = y² + 6y
Thus we arrive at a quadratic equation. Let us solve this now,
y² + 6y - 27 = 0
y² + 9y - 3y - 27 = 0
y(y+9)-3(y+9) = 0
(y-3)(y-9) = 0
The roots of the above quadratic equation are thus 3 and −9.
Thus the value of ‘y’ could either be 3 or -9.

Page No 6.16

Ques.36. If the point P(k − 1, 2) is equidistant from the points A(3, k) and B(k, 5), find the values of k.
Ans. It is given that P(k − 1, 2) is equidistant from the points A(3, k) and B(k, 5).
∴ AP = BP
(Distance formula)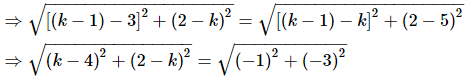

Squaring on both sides, we get
k²−8k+16+4−4k+k²=10
⇒2k²−12k+10=0
⇒k²−6k+5=0
⇒(k−1)(k−5)=0
⇒k−1=0 or k−5=0
⇒k=1 or k=5
Thus, the value of k is 1 or 5.

Page No 6.17

Ques.37. If the point A(0, 2) is equidistant from the points B(3, p) and C(p, 5), find p. Also, find the length of AB.
Ans. It is given that A(0,2) is equidistant from the points B(3, p) and C(p, 5).
∴ AB = AC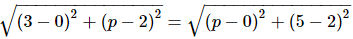
 (Distance formula)
Squaring on both sides, we get
9+p²−4p+4=p²+9
⇒−4p+4=0
⇒p=1
Thus, the value of p is 1.
∴ AB =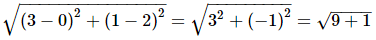
= √10 units

Page No 6.17

Ques.38. Name the quadrilateral formed, if any, by the following points, and given reasons for your answers:
(i) A(−1,−2) B(1, 0), C (−1, 2), D(−3, 0)
(ii) A(−3, 5) B(3, 1), C (0, 3), D(−1, −4)
(iii) A(4, 5) B(7, 6), C (4, 3), D(1, 2)
Ans. (i) A (−1,−2) , B(1,0), C(−1,2), D(−3,0)
Let A, B, C and D be the four vertices of the quadrilateral ABCD.
We know the distance between two points P(x₁,y₁) and (x₂,y₂) Qis given by distance formula: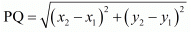

Hence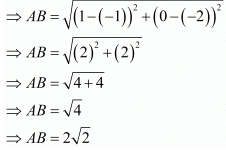

Similarly,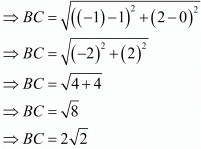

Similarly,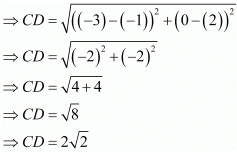

Also,

Hence from above we see that all the sides of the quadrilateral are equal. Hence it is a square.
(ii) A (−3,5) , B(3,1), C(0,3), D(−1,−4)
Let A, B, C and D be the four vertices of the quadrilateral ABCD.
We know the distance between two points P(x₁,y₁) and Q(x₂,y₂) is given by distance formula: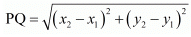

Hence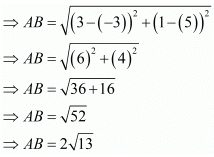

Similarly,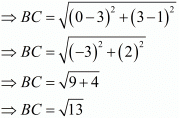

Similarly,

Also,

Hence from the above we see that it is not a quadrilateral
(iii) A (4, 5), B (7,6), C(4,3), D(1,2)
Let A, B, C and D be the four vertices of the quadrilateral ABCD.
We know the distance between two points P(x₁,y₁) and Q(x₂,y₂) is given by distance formula: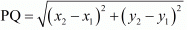

Hence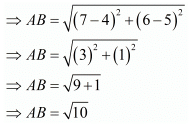

Similarly,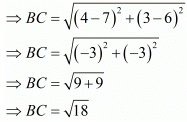

Similarly,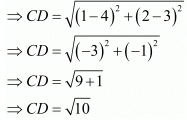

Also,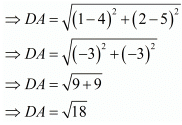

Hence from above we see that
AB = CD and BC = DA
Here opposite sides of the quadrilateral is equal. Hence it is a parallelogram.

Page No 6.17

Ques.39. Find the equation of the perpendicular bisector of the line segment joining points (7, 1) and (3,5).
Ans. TO FIND: The equation of perpendicular bisector of line segment joining points (7, 1) and (3, 5)
Let P(x, y) be any point on the perpendicular bisector of AB. Then,
PA = PB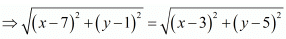

⇒(x-7)² + (y-1)² = (x-3)² + (y-5)²
⇒x² -14x+49+y²-2y+1=x²-6x+9+y²-10y+25
⇒-14x+6x+10y-2y+49+1-9-25=0
⇒-8x+8y+16=0
⇒x-y-2=0
⇒x-y=2
Hence the equation of perpendicular bisector of line segment joining points (7, 1) and (3, 5) is x-y=2

Page No 6.17

Ques.40. Prove that the points (3, 0), (4, 5), (−1, 4) and (−2 −1), taken in order, form a rhombus. Also, find its area.
Ans. The distance d between two points (x₁,y₁) and (x₂,y₂) is given by the formula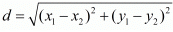

In a rhombus all the sides are equal in length. And the area ‘A’ of a rhombus is given as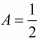
(Product of both diagonals)
Here the four points are A(3,0), B(4,5), C(−1,4) and D(−2,−1).
First let us check if all the four sides are equal.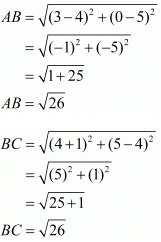


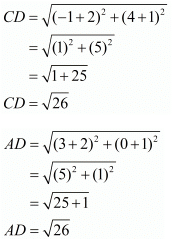
Here, we see that all the sides are equal, so it has to be a rhombus.
Hence we have proved that the quadrilateral formed by the given four vertices is a rhombus.
Now let us find out the lengths of the diagonals of the rhombus.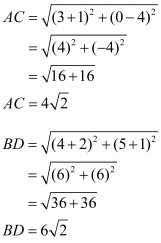

Now using these values in the formula for the area of a rhombus we have,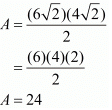

Thus the area of the given rhombus is 24 square units.

Page No 6.17

Ques.41. In the seating arrangement of desks in a classroom three students Rohini, Sandhya and Bina are seated at A(3, 1), B(6, 4), and C(8, 6). Do you think they are seated in a line?
Ans. The distance d between two points (x₁,y₁) and (x₂,y₂) is given by the formula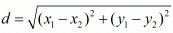

For three points to be collinear the sum of distances between any two pairs of points should be equal to the third pair of points.
The given points are A(3,1), B(6,4) and C(8,6).
Let us find the distances between the possible pairs of points.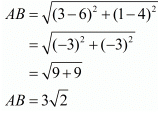


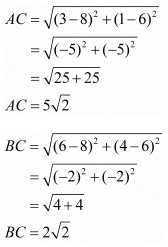
We see that AB+BC=AC.
Since sum of distances between two pairs of points equals the distance between the third pair of points the three points must be collinear. Hence, the three given points are collinear.

Page No 6.17

Ques.42. Find a point on y-axis which is equidistant form the points (5, −2) and (−3, 2).
Ans. The distance d between two points (x₁,y₁) and (x₂,y₂) is given by the formula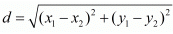

Here we are to find out a point on the y−axis which is equidistant from both the points A(5,−2) and B(−3,2).
Let this point be denoted as C(x, y).
Since the point lies on the y-axis the value of its ordinate will be 0. Or in other words we have.
Now let us find out the distances from ‘A’ and ‘B’ to ‘C’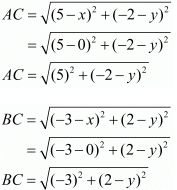

We know that both these distances are the same. So equating both these we get,
AC = BC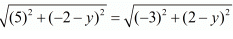

Squaring on both sides we have,
(5)² + (-2-y)² = (-3)² + (2-y)²
25+4+y²+4y = 9+4+y²-4y
8y=-16
y=-2
Hence the point on the y-axis which lies at equal distances from the mentioned points is (0,-2).

Page No 6.17

Ques.43. Find a relation between x and y such that the point (x, y) is equidistant from the points (3, 6) and (−3, 4).
Ans. The distance d between two points (x₁,y₁) and (x₂,y₂) is given by the formula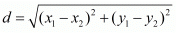

Let the three given points be P(x, y), A(3,6) and B(−3,4).
Now let us find the distance between ‘P’ and ‘A’.

Now, let us find the distance between ‘P’ and ‘B’.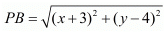

It is given that both these distances are equal. So, let us equate both the above equations,
PA = PB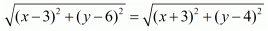

Squaring on both sides of the equation we get,
(x-3)² + (y-6)² = (x+3)² + (y-4)²
x²+9-6x+y²+36-12y = x²+9+6x+y²+16-8y
12x+4y = 20
3x+y = 5
Hence the relationship between ‘x’ and ‘y’ based on the given condition is 3x+y=5.

Page No 6.17

Ques.44. If a point A(0, 2) is equidistant from the points B(3, p) and C(p, 5), then find the value of p.
Ans. It is given that A(0, 2) is equidistant from the points B(3, p) and C(p, 5).
∴ AB = AC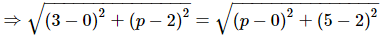
(Distance formula)
Squaring on both sides, we get
9+p²−4p+4 = p²+9
⇒−4p+4=0
⇒p=1
Thus, the value of p is 1.

Page No 6.17

Ques.45. Prove that the points (7, 10), (−2, 5) and (3, −4) are the vertices of an isosceles right triangle.
Ans. Let the given points be A(7, 10), B(−2, 5) and C(3, −4).
Using distance formula, we have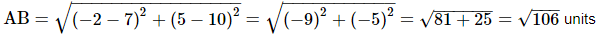

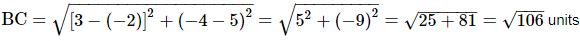
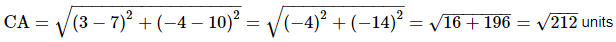
Thus, AB = BC = √106 units
∴ ∆ABC is an isosceles triangle.
Also,
AB² + BC² = 106 + 106 = 212
and CA² = 212
∴ AB² + BC² = CA²
So, ∆ABC is right angled at B.(Converse of Pythagoras theorem)
Hence, the given points are the vertices of an isosceles right triangle.