Chapter 10 - Circles, RD Sharma Solutions - (Part - 1) | RD Sharma Solutions for Class 10 Mathematics PDF Download
Page No 8.33
Q.1. If PT is a tangent at T to a circle whose centre is O and OP = 17 cm, OT = 8 cm, Find the length of the tangent segment PT.
Ans. Let us put the given data in the form of a diagram.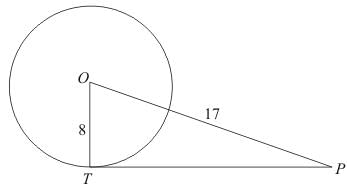
We have to find TP. From the properties of tangents we know that a tangent will always be at right angles to the radius of the circle at the point of contact. Therefore is a right angle and triangle OTP is a right triangle.
We can find the length of TP using Pythagoras theorem. We have,
TP2 = OP2 - OT2
TP2 = 172 - 82
TP2 = (17 - 8)(17 + 8)
TP2 = 9 x 25
TP2 = 255
TP = √225
TP = 15
Therefore, the length of TP is 15 cm.
Q.2. Find the length of a tangent drawn to a circle with radius 5 cm, from a point 13 cm from the centre of the circle.
Ans. Let us first put the given data in the form of a diagram.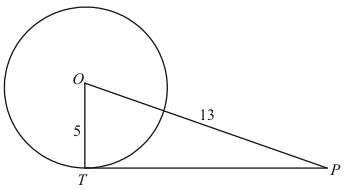
We have to find TP. From the properties of tangents we know that a tangent will always be at right angles to the radius of the circle at the point of contact. Therefore ∠OTP is a right angle and triangle OTP is a right triangle.
We can find the length of TP using Pythagoras theorem. We have,
TP2 = OP2 - OT2
TP2 = 132 - 52
TP2 = (13 - 5)(13 + 5)
TP2 = 8 x 18
TP2 = 144
TP = √144
TP = 12
Therefore, the length of TP is 12 cm.
Q.3. A point P is 26 cm away from the centre O of a circle and the length PT of the tangent drawn from P to the circle is 10 cm. Find the radius of the circle.
Ans. Let us put the given data in the form of a diagram.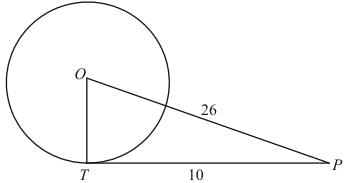
We have to find OT. From the properties of tangents we know that a tangent will always be at right angles to the radius of the circle at the point of contact. Therefore ∠OTP is a right angle and triangle OTP is a right triangle.
We can find the length of TP using Pythagoras theorem. We have,
OT2 = OP2 - TP2
OT2 = 262 - 102
OT2 = (26 - 10)(26 + 10)
OT2 = 16 x 36
OT2 = 576
TP = √576
TP = 24
Therefore, the radius of the circle is 24 cm.
Q.4. If from any point on the common chord of two interesting circle, tangents be drawn to the circles, prove that they are equal.
Ans. Let the two circles intersect at points X and Y. XY is the common chord.
Suppose A is a point on the common chord and AM and AN be the tangents drawn from A to the circle.
We need to show that AM = AN.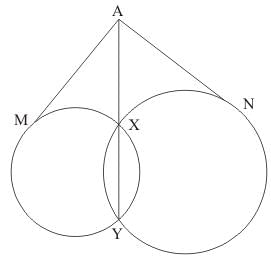
In order to prove the above relation, following property will be used.
“Let PT be a tangent to the circle from an external point P and a secant to the circle through P intersects the circle at points A and B, then PT 2 = PA × PB”.
Now, AM is the tangent and AXY is a secant.
∴ AM2 = AX × AY ...(1)
AN is the tangent and AXY is a secant.
∴ AN2 = AX × AY ...(2)
From (1) and (2), we have
AM2 = AN2
∴ AM = AN
Q.5. If the sides of a quadrilateral touch a circle. prove that the sum of a pair of opposite sides is equal to the sum of the other pair.
Ans. Let us first put the given data in the form of a diagram.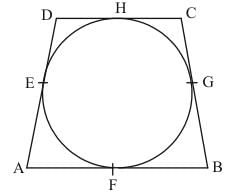
We have been asked to prove that the sum of the pair of opposite sides of the quadrilateral is equal to the sum of the other pair.
Therefore, we shall first consider,
AB + DC
But by looking at the figure we have,
AB + DC = AF + FB + DH + HC …… (1)
From the property of tangents we know that the length of two tangents drawn to a circle from a common external point will be equal. Therefore we have the following,
AF = AE
FB = BG
DH = ED
HC = CG
Replacing for all the above in equation (1), we have
AB + DC = AE + BG + ED + CG
AB + DC = (AE + ED) + (BG +CG)
AB + DC = AD + BC
Thus we have proved that the sum of the pair of opposite sides of the quadrilateral is equal to the sum of the other pair.
Q.6. Out of the two concentric circles , the radius of the outer circle is 5 cm and the chord AC of length 8 cm is a tangent to the inner circle . Find the radius of the inner circle.
Ans.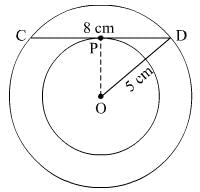
Let the centre of the two concentric circles be O.
CD is the tangent to the inner circle.
OP joins the centre of the circle to the tangent at the point of contant.
OP ⊥ CD and OP bisects CD.
Thus, PD = 4 cm
In ∆OPD,
OP2 + PD2 = OD2
⇒ OP2 = OD2 − PD2
⇒ OP2 = (5)2 − (4)2 = 25 − 16 = 9
⇒ OP=3 cm
Hence, the radius of the inner circle = 3 cm.
Q.7. A chord PQ of a circle is parallel to the tangent drawn at a point R of the circle . Prove that R bisects the arc PRQ.
Ans.
Given: Circle with centre O. PQ is the chord parallel to the tangent l at R
To prove: The point R bisects the arc PRQ.
Construction: Join OR intersecting PQ at S.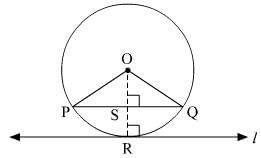
Proof:
OR ⊥ l (Radius is perpendicular to the tangent at the point of contact)
PQ || l (given)
∴∠OSP = ∠OSQ = 90° (pair of corresponding angles)
In ΔOPS and ΔOQS
OP = OQ (Radii of the same circle)
OS = OS (Common)
∠OSP = ∠OSQ (Proved)
So,ΔOPS ≅ ΔOQS (RHS congruence criterion)
⇒ ∠POS = ∠QOS (C.P.C.T)
⇒ arc (PR) = arc (QR) (Measure of the arc is same as the angle subtended by the arc at the centre)
Thus, the point R bisects the arc (PRQ).
Q.8. Prove that a diameter AB of a circle bisects all those chords which are parallel to the tangent at that point A .
Ans. Consider a circle with centre at O. l is tangent that touches the circle at painted to the circle at point A. Let AB is diameter. Consider a chord CD parallel to l. AB intersects CD at point Q.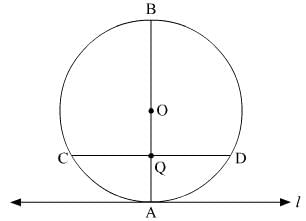
To prove the given statement, it is required to prove CQ = QD
Since l is tangent to the circle at point A.
∴ AB ⊥ l
It is given that l || CD
Since CD is a chord of the circle and OA ⊥ l.
Thus, OQ bisects the chord CD.
This means AB bisects chord CD.
This means CQ = QD.
Q.9. If AB, AC, PQ are tangents in the given figure and AB = 5 cm, find the perimeter of Δ APQ.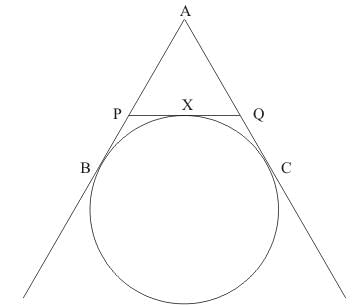
Ans. We have been asked to find the perimeter of the triangle APQ.
Therefore,
Perimeter of ΔAPQ is equal to AP + AQ + PQ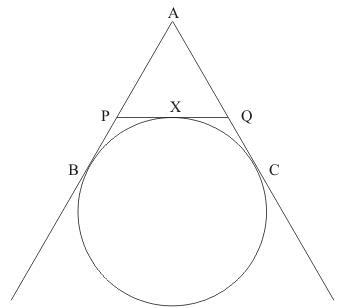
By looking at the figure, we can rewrite the above as follows,
Let the Perimeter of ΔAPQ be P. So P= AP + AQ + PX + XQ
From the property of tangents we know that when two tangents are drawn to a circle from the same external point, the length of the two tangents will be equal. Therefore we have,
PX =PB
XQ =QC
Replacing these in the above equation we have,
P =AP + AQ + PB + QC
From the figure we can see that,
AP + PB = AB
AQ + QC = AC
Therefore, we have, P= AB + AC
It is given that AB = 5 cm.
Again from the same property of tangents we know that that when two tangents are drawn to a circle from the same external point, the length of the two tangents will be equal. Therefore we have,
AB = AC
Therefore,
AC = 5 cm
Hence,
P = 5 + 5=10
Thus the perimeter of triangle APQ is 10 cm.
Page No 8.34
Q.10. Prove that the intercept of a tangent between two parallel tangents to a circle subtends a right angle at the centre.
Ans.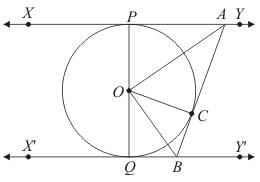
Given: XY and X′Y′ at are two parallel tangents to the circle with centre O and AB is the tangent at the point C, which intersects XY at A and X′Y′ at B.
To Prove: ∠AOB = 90°
Construction: Let us joint point O to C.
Proof:
In ΔOPA and ΔOCA, we have
OP = OC (Radii of the same circle)
AP = AC (Tangents from point A)
AO = AO (Common side)
ΔOPA ≅ ΔOCA (SSS congruence criterion)
Therefore, ∠POA = ∠COA ……(i) (C.P.C.T)
Similarly, ΔOQB ≅ ΔOCB ……(ii)
Since POQ is a diameter of the circle, it is a straight line.
Therefore, ∠POA + ∠COA + ∠COB + ∠QOB = 180°
From equations (i) and (ii), it can be observed that
2∠COA + 2∠COB = 180°
∴ ∠COA + ∠COB = 90°
So, ∠AOB = 90°.
Q.11. In the given figure, PQ is tangent at a point R of the circle with centre O. If ∠TRQ = 30°, find m ∠PRS.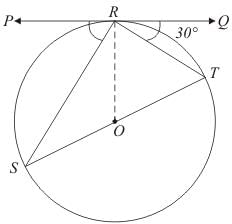
Ans. We have been given that ∠TRQ = 30°
From the property of tangents we know that a tangent will always be perpendicular to the radius at the point of contact. Therefore,
∠QRO = 90°
Looking at the given figure we can rewrite the above equation as follows,
∠TRQ + ∠TRO = 90°
We know that ∠TRQ = 30°. Therefore,
30° + ∠TRO = 90°
∠TRO = 60°
Now consider ΔTRO. The two sides of this triangle OR and OT are nothing but the radii of the same circle. Therefore,
OR = OT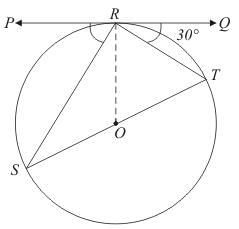
And hence ΔTRO is an isosceles triangle. We know that the angles opposite to the equal sides of the isosceles triangle will be equal. Therefore,
∠TRO = ∠OTR
We have found out that ∠TRO = 60°. Therefore,
∠OTR = 60°
Now consider ΔTRO. We know that sum of all angles of a triangle will always be equal to 180° Therefore,
∠TRO + ∠OTR + ∠TOR = 180°
60° + 60° + ∠TOR = 180°
∠TOR = 60°
Now let us consider the straight line SOT. We know that the angle of a straight line is 180°. Therefore,
∠SOT = 180°
From the figure we can see that,
∠SOT = ∠SOR + ∠TOR
That is,
∠SOR + ∠TOR = 180°
We have found out that ∠TOR = 60°. Therefore,
∠SOR + 60° = 180°
∠SOR = 120°
Let us take up ΔSOR now. The sides SO and OR of this triangle are nothing but the radii of the same circle and hence they are equal. Therefore, ΔSOR is an isosceles triangle. In an isosceles triangle, the angles opposite to the two equal sides of the triangle will be equal. Therefore we have,
∠OSR = ∠ORS
Also the sum of all angles of a triangle will be equal to 180°. Therefore,
∠SOR + ∠ORS + ∠OSR = 180°
∠SOR + 2∠ORS = 180°
In the previous step we have found out that ∠SOR = 120°. Therefore,
120° + 2∠ORS = 180°
2∠ORS = 60°
∠ORS = 30°
Let us now take up ∠ORPWe know from the property of tangents that the angle between the radius of the circle and the tangent at the point of contact will be equal to 90°. Therefore,
∠ORP = 90°
By looking at the figure we can rewrite the above equation as follows,
∠PRS + ∠ORS = 90°
In the previous section we have found that ∠ORS = 30°. Therefore,
∠PRS + 30° = 90°
∠PRS = 60°
Thus we have found out that ∠PRS = 60°.
Q.12. If PA and PB are tangents from an outside point P such that PA = 10 cm and ∠APB = 60°. Find the length of chord AB.
Ans.
Let us first put the given data in the form of a diagram.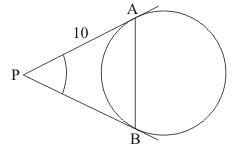
From the property of tangents we know that the length of two tangents drawn to a circle from a common external point will always be equal. Therefore,
PA=PB
Consider the triangle PAB. Since we have PA=PB, it is an isosceles triangle. We know that in an isosceles triangle, the angles opposite to the equal sides will be equal. Therefore we have,
∠PAB = ∠PBA
Also, sum of all angles of a triangle will be equal to 180°. Therefore,
∠PAB + ∠PBA + ∠APB = 180°
60° + 2∠PBA = 180°
2∠PBA = 120°
∠PBA = 60°
Since we know that ∠PAB = ∠PBA,
∠PAB = 60°
Now if we see the values of all the angles of the triangle, all the angles measure 60° Therefore triangle PAB is an equilateral triangle.
We know that in an equilateral triangle all the sides will be equal.
It is given in the problem that side PA = 10 cm. Therefore, all the sides will measure 10 cm. Hence, AB = 10 cm.
Thus the length of the chord AB is 10 cm.
FAQs on Chapter 10 - Circles, RD Sharma Solutions - (Part - 1) - RD Sharma Solutions for Class 10 Mathematics
| 1. What are the properties of circles according to RD Sharma Solutions for Class 10? |  |
| 2. How can we find the area of a circle using RD Sharma Solutions for Class 10? |  |
| 3. What are the different types of circles discussed in RD Sharma Solutions for Class 10? |  |
| 4. How can we calculate the circumference of a circle in RD Sharma Solutions for Class 10? |  |
| 5. Can you explain the concept of the chord of a circle as per RD Sharma Solutions for Class 10? |  |

|
Explore Courses for Class 10 exam
|

|

















